基于阶次跟踪和总体经验模式分解相结合的滚动轴承升速过程的故障诊断方法研究

2015-04-25任学平邢义通王建国辛向志张玉皓

制造业自动化 2015年2期

任学平，邢义通，王建国，辛向志，张玉皓

REN Xue-ping, XING Yi-tong, WANG Jian-guo, XIN Xiang-zhi, ZHANG Yu-hao

（内蒙古科技大学机械工程学院，包头 014010）

0 引言

滚动轴承不仅是旋转机械中应用广泛、要求严格的通用零部件之一，而且还是最易损坏的的零部件之一。由于其经常工作在转速高、负荷大的工况下，造成滚动轴承的故障多发。而且其运行状态的好坏对机械设备整体的工作性能具有深远影响。所以对滚动轴承故障进行有效地诊断至关重要[1]。

目前针对滚动轴承故障的诊断方法有很多种，但是由于在升速过程中，滚动轴承振动信号具有非平稳性的特点，如果直接采用FFT变换对其进行处理,结果将造成频率混叠现象，难以提取故障信息。针对这一问题，本文提出了一种基于阶次跟踪和总体经验模态分解相结合的诊断方法。通过实验案例分析,得到了预期的结果。

1 基本理论

1.1 阶次跟踪

旋转机械的振动与转速之间存在密切关系，在升速的工况下，转速的变化会引起转频随之变化，这就造成了振动信号非平稳性的特点。如果采用传统的频谱分析方法对此类信号进行诊断难以提取故障信息。然而阶次分析则有效的解决了这种问题，其通过插值计算方法将等时间间隔采样转化为等角度间隔采样，实现了由传统的频谱分析向阶次谱分析的过渡。阶次跟踪的难点在于如何通过等时间间隔采样的时间序列求得等角度采样的时间序列。

计算阶次跟踪法(Computed Order Tracking,简称COT)是将采集的原始时域振动信号和转速脉冲信号相结合，通过插值计算，使具有非平稳性特点的振动信号转化为平稳的角域信号。其与传统的阶次跟踪相比不仅使测试精度有了一定的提高，而且由于其无需特定的硬件，所以使测试成本也大大降低。

COT算法的难点在于如何获取等角度间隔采样的时间序列，具体过程如下：参考转速的转角θ可以表达为如下形式：

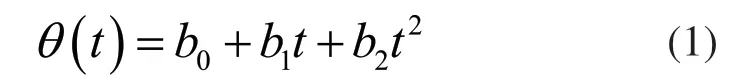
在式（1）中，b0，b1，b2为待定系数，将3个依次到达的脉冲时间点(t1、t2、t3)和转角增量 θΔ 代入式(1)，即：

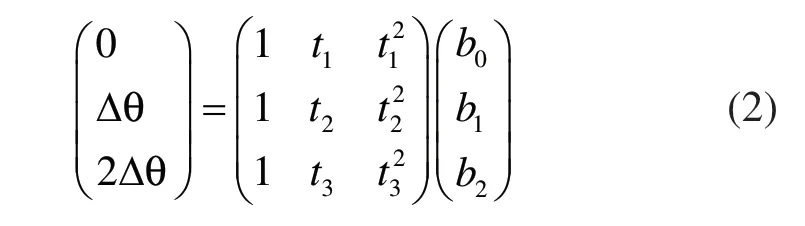
由上式求出bi后，将其代入式（2）求解可得对应转角变化的时间：

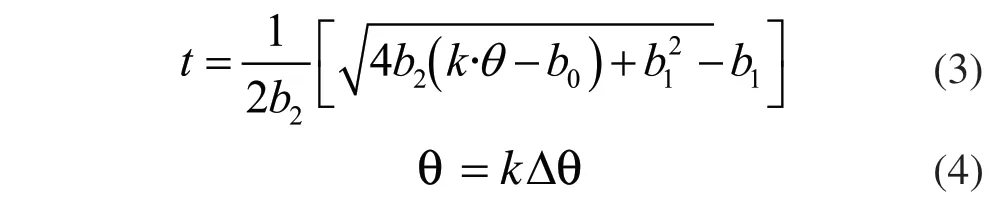
在式（3）中，k为插值系数，由式（4）决定。根据所求出的时间值，利用插值算法可以求出振动信号对应的幅值，再对其进行相应的处理[2]。

1.2 总体经验模式分解

总体经验模式分解（Ensemble empirical mode decomposition，简称EEMD）是一种针对非平稳性微弱故障信号的现代时频分析方法。它的优点在于克服了在EMD分解中，由于IMF分量的不连续而引起的“模式混叠”现象。其分解的实质是：在原始振动信号中，人为地引入高斯白噪声，由于高斯白噪声是一种频率均匀分布的噪声信号，这样就能使原始信号在不同尺度上具有连续性，然后再对信号进行多次EMD分解，最终以各IMF分量的平均值作为分解结果，这样就有效的克服了EMD分解的不足，提高了抗混叠效果。

EEMD算法如下：

1）给原始信号x(t)加入等长度的频率均匀分布白噪声序列，并进行归一化处理：

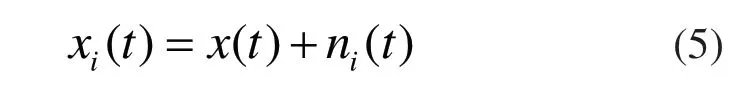
2）对xi(t)信号进行EMD分解，等到不同的IMF分量cij(t)和余项ri(t)。cij(t)表示第i次加入白噪声后分解得到的第j个分量。

3）对不同次的cij(t)求取平均值，得到最终的IMF分量。

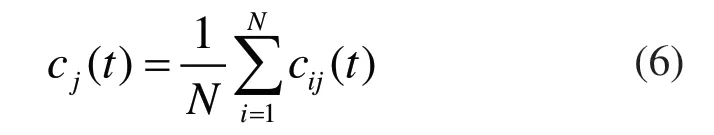
式（6）中：cj(t)表示最终的IMF分量。

1.3 滚动轴承故障信号分析的具体步骤

利用阶次跟踪和EEMD分解相结合的方式对滚动轴承故障进行诊断的步骤如下：

1）利用阶次跟踪将采集到的时域信号转化为角域信号。

2）对得到的角域信号进行EEMD分解。得到不同的IMF分量。

3）应用互相关、峭度准则对IMF分量进行有效提取。

4）对提取到的IMF分量，进行阶次谱分析。

为了证明此理论方法的实效性，本文通过实验案例进行了验证。

2 实验案例分析

本次实验使用的试验台是美国Spectra Quest公司设计制造的机械故障综合模拟试验台，试验台如图1所示。本实验从轴向和径向两个不同的方向，用三个加速度传感器对含有外圈故障的滚动轴承进行了振动信号的采集，其测点位置如图1所示，同时通过光电传感器对转速脉冲信号进行了采集。实验中使用的采集仪器是ZonicBook/618E，其不仅可以对转速脉冲、振动烈度、振动加速度等信号进行直接采集, 而且还可以对采集的信号直接进行频谱分析。实验采用的故障轴承为ER-10K圆柱滚子轴承，在不影响使用的情况下，人为地设置了外圈故障。

ER-10K圆柱滚子轴承的几何尺寸为：

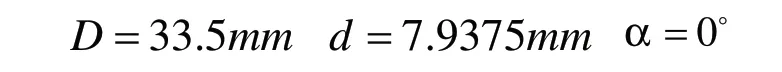
该轴承的特征频率计算公式如下：

在式（7）中：

fouter为外圈故障时滚动轴承的特征频率；

fr为滚动轴承内圈的转动频率；

d为滚动体直径；

D为轴承中径；

α 为接触角。

因此轴承的故障特征频率为：

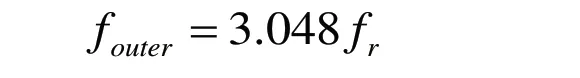
所以其故障特征阶次为：

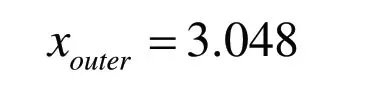
在本次实验中，振动信号的采样频率为2560Hz，实际的采样点数为N=10001。图2和图3分别为采集的时域振动信号和转速脉冲信号。

先对由光电传感器测得的脉冲信号求取转速信号如图4所示，通过图4可以看出本实验模拟的是滚动轴承升速的工作过程。

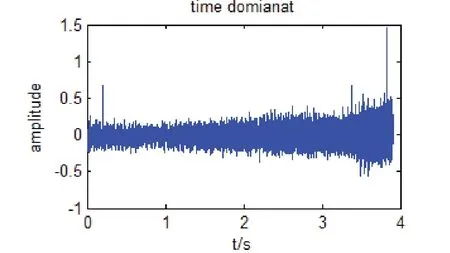
图2 时域振动信号

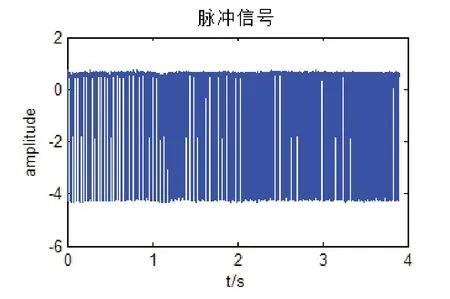
图3 转速脉冲

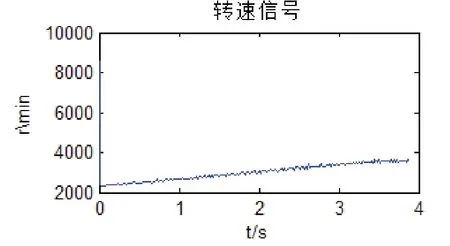
图4 转速信号

再对时域振动信号进行FFT变换，得到频率谱图，如图5所示。

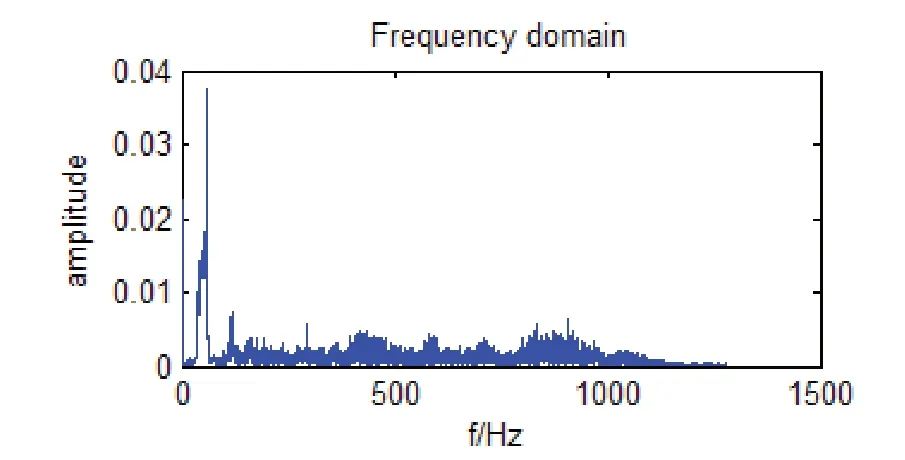
图5 信号的频率谱图

通过观察图5发现，频率谱图存在严重的频率模糊。因此得出结论，如果用传统的频谱分析法分析非稳态信号，将不能有效地提取故障信息。所以要对信号作进一步的处理，将时域振动信号和转速脉冲信号相结合，通过插值计算的方式，进行等角度间隔重采样，得到角域信号如图6所示。对角域信号进行阶次谱分析如图7所示，可以明显看出效果不是很理想。

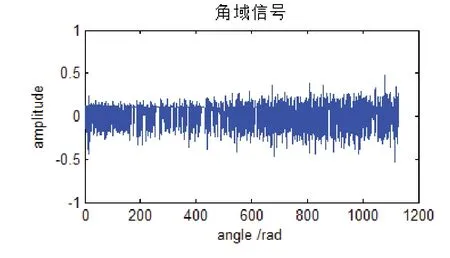
图6 角域信号

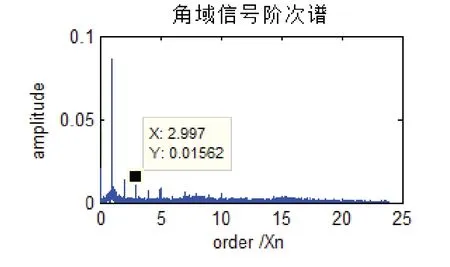
图7 角域信号阶次谱

表1 各分量的相关系数和峭度值

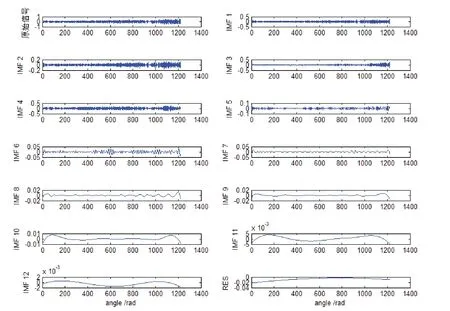
图8 EEMD分解结果

因此对角域信号进行EEMD分解（加入0.2倍的白噪声，进行100次EMD分解），得到数据矩阵共有14行，第一行为原始信号，从第二行开始到第十三行，共有12个有效的IMF分量，最后一行为残余分量。如图8所示，对12个有效地IMF分量求取相关系数和峭度值如表1所示。根据互相关准则可知，相关系数值不能超过1，所以把IMF5分量剔除，而IMF3分量和IMF4分量的相关系数较大，进而保留。而相对于峭度值分析，IMF3分量明显大于IMF4分量。综合上述结果，最终选取IMF3分量作为数据的有效分量。最后对IMF3分量作阶次谱分析，如图9所示。

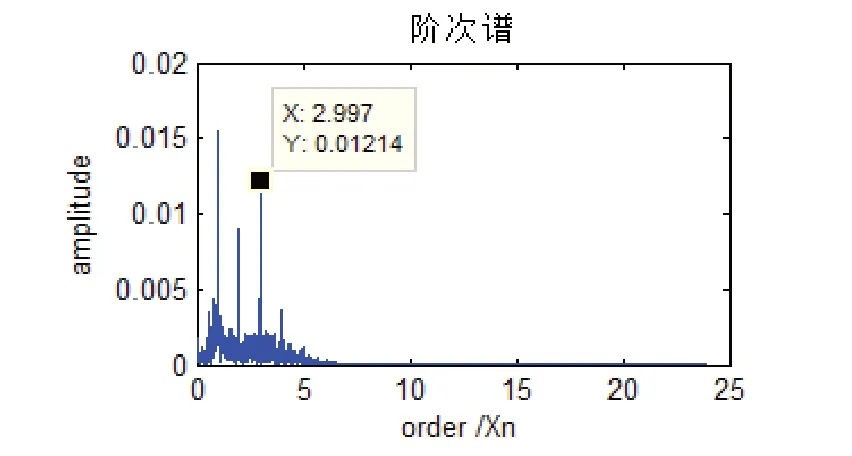
图9 阶次谱图

对比图7和图9，可以看出：直接对角域信号进行阶次谱分析和对角域信号进行EEMD分解，再对提取到的分量进行阶次谱分析，两者都可以得x=2.997的阶比，和外圈故障阶比xouter=3.048十分接近，表明两者都能够诊断出外圈故障。但是相比于直接进行阶次谱分析，进行EEMD分解后的阶次谱分析则抑制了我们不需要分析的部分，间接的使外圈故障阶比更加突显，使结果更加直观。因此证明了本理论方法的有效性。