超短波对数周期天线阵等效幅相误差的求解方法
2015-04-25姚述福储飞黄
姚述福,储飞黄,瞿 洋
(电子工程学院,合肥 230037)
0 引 言
对数周期天线阵列因其宽频域、高增益的特性,被广泛应用于短波、超短波、微波等波段的通信、测向、搜索、电子对抗等。现役某些通信对抗装备就是利用对数周期天线阵进行空间功率合成形成高功率电场来对敌进行通信干扰[13]。在这些装备的实际使用中,对数周期天线阵的参数和合成效率的准确测量问题一直无法得到解决,极大地影响了该装备的作战效能。
针对该类型对数周期天线阵的单元结构和阵列结构比较复杂、体积结构较大导致的参数测量难题,本文提出了测量对数周期天线等效幅相误差的方法。即将天线阵等效为无互耦的天线阵,并利用该天线阵发送多路码分多址(CDMA)信号,在远场对该多路信号进行测量,将各路发送的CDMA信号区分开来,避开天线阵结构和天线互耦的影响,从而得到天线阵的幅相变化参数[45]。
1 对数周期天线阵的等效处理
应用于空间功率合成的对数周期天线阵,在其工作时的瞄准方向为天线阵的边射方向,即垂直于天线阵的方向,因而在远场测量该天线系统的合成功率和幅相误差时也只有在该方向上有显著意义和实用价值。另外,为了简化测量与计算,需要对天线阵进行等效处理来简化计算步骤。因此天线阵进行了等效处理。
1.1 将对数周期天线单元等效为有方向的点源
由文献可知,对数周期天线在某一频率上工作时,可以将其等效为一个具有对数周期天线单元方向图的点源,即天线电波全由该点源发射[67]。图1为单个对数后周期天线的E面和H面方向图,为了计算更加精确,取方向图最大方向的邻近角度区域,在这个角度区域内的方向图函数值为一个常数,即可以认为该方向图函数是一个点源在这个角度区域内发射球面波[89]。
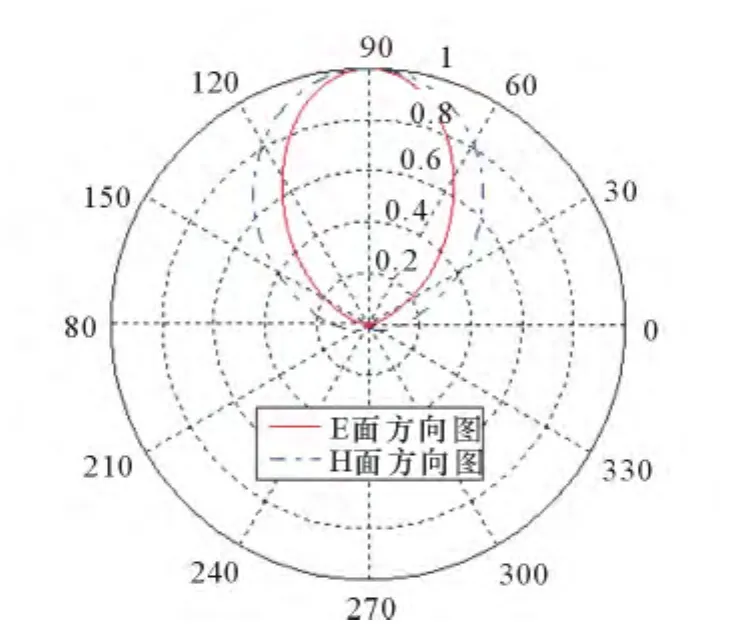
图1 单个对数周期天线单元的方向图
1.2 将天线单元间互耦形成的互阻抗等效为天线单元的自阻抗
待测天线阵结构复杂,单个对数周期天线的各个偶极子天线之间存在耦合,而且各个对数周期天线单元之间也存在耦合[10]。这里将该天线阵等效为只有自阻抗而无互阻抗的点源阵,就是将某一特定单元与其它单元产生的互阻抗等效为该单元本身阻抗的一部分。考虑一个N元的点源阵在远场接收信号时,有:

式中:Γ为各不同阵元到测量点的波程对电磁波传播的影响。
即发射端第n路电流I n对天线阵的激励在远场点得到场强为因此,可以把在该远场测量点的第n路单元的互阻抗、自阻抗之和还有波程对其影响之和等效为它的自阻抗。显然,En=InΗn是第n个激励电流I n在远场某一测量点产生的接收信号场强,既包括第n个阵元直接辐射的信号,也包括与其他它阵元的互阻抗产生激励的影响。
由此可见,从接收点来看,上述实际天线阵可以看成激励为In不变、各阵元自阻抗为H n但没有互耦效应的理想阵列天线。
2 等效阵的远场场强公式
针对得到天线阵的幅相误差这一目的,需要将天线阵的远场场强公式表达为区分幅度和相位2个部分的形式,进而可以分别计算幅度和相位差异。
上一节将对数周期天线阵单元简化为一个有方向的点源组成的点源阵,且阵元之间无互耦,根据点源的场强公式将远场场强公式进行简化,在远场得到第n个阵元产生的电场强度为[11]:
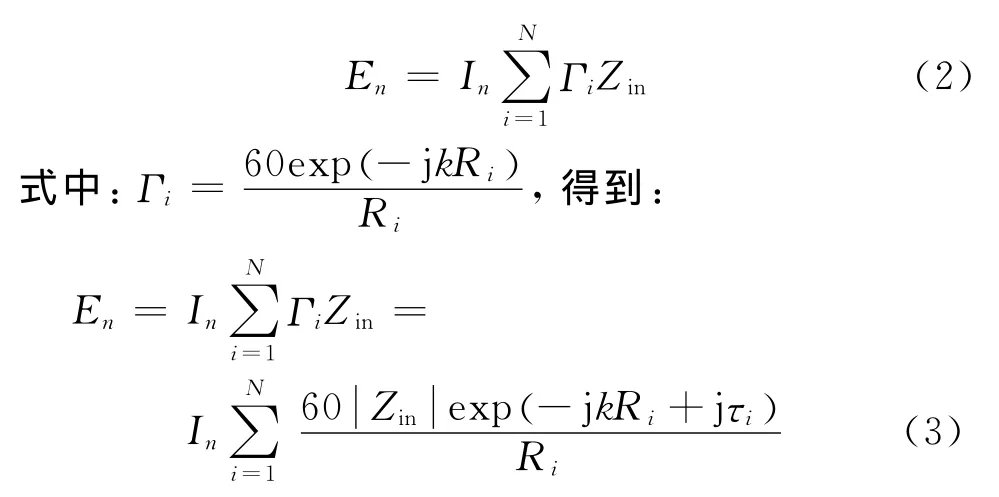
式中:将所有第n路单元用复数表示的阻抗和互阻抗用表示,即区分幅度和相位部分。
而在接收该信号时,多通道CDMA接收机得到的信号就是由式(3)得到的数值,因而将式(3)表示为:
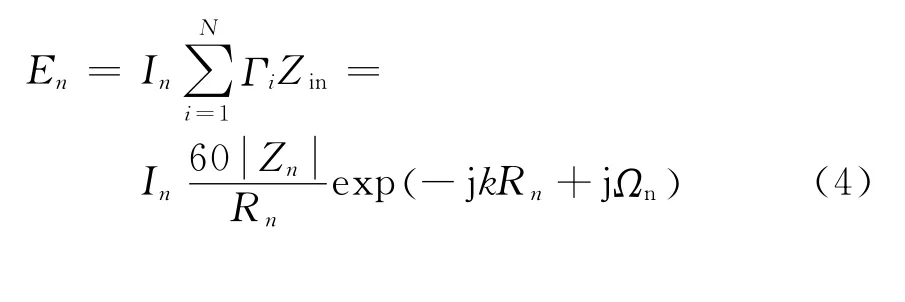
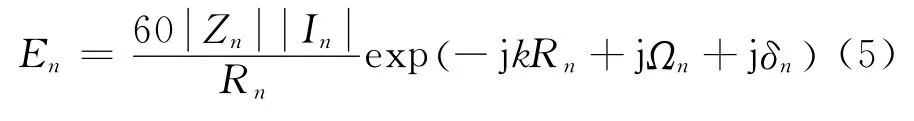
式中:En为将天线阵等效为无互阻抗时由第n个阵元得到的在测量点的场强;Rn为第n个阵元到测量点的距离;Ωn表示天线的阻抗对相位的影响。
3 幅度值和相位差异的测量与计算过程
测量分为2个部分,天线阵元、测量点的位置测量;多路CDMA信号的测量。位置测量可以通过GPS直接测量得到。对多路CDMA信号的测量则通过多通道CDMA信号接收机接收,由于CDMA信号间的弱相关性,在接收机端可以很容易地将各路信号区分出来,并得到信号的幅度值和不同信号间的相位差值。根据信号间的相位差值就可以计算出天线单元间的相位差值。
3.1 阵元和测量点的GPS定位值
整个计算需要测量的点分为天线阵等效点源的位置及一个远场测量点的位置和测得的数据。在测量阵元的定位值时,考虑到将对数周期天线阵等效为点源阵,所以需要计算各阵元的等效位置。首先根据给定的工作频率和天线的特性计算得到该点位于对数天线单元轴上的位置,再通过GPS定位设备测得该位置的三维坐标。
3.2 方向图函数值中幅度分量的计算
前面通过GPS测得了等效点源的位置与测量点的位置,因此可以得到各个阵元与测量点的波程Rn。另外通过CDMA信号接收机可以得到各路信号的幅度值因此对式(5)求模可以得到:
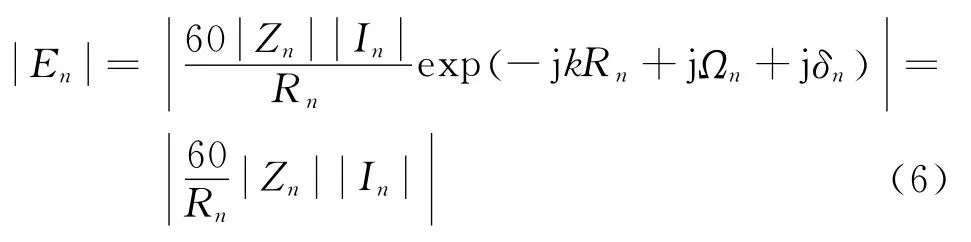
3.3 天线阵元间相位差异的计算
在实际应用中研究的对数周期天线阵属于2×4的矩形布阵,因此将其等效为点源阵时也为矩形阵,需要采用矩形阵的计算方法来进行计算。下面给出等效为点源后的天线布阵图,其中角度τ为天线阵与铅垂线的夹角,OA为在该布阵下最大方向。
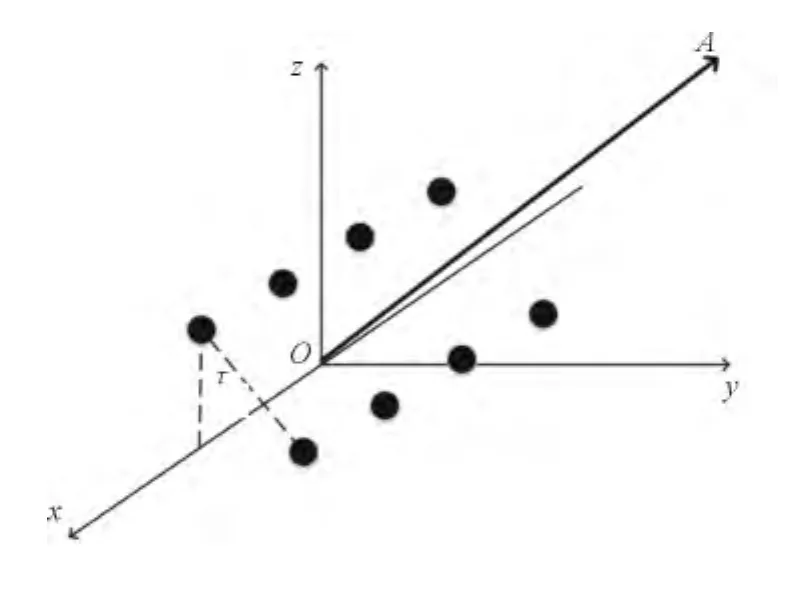
图2 等效源后的对数周期天线阵
由式(5)可知表示阵元间相位差值由指数函数部分表达,而式中表示各阵元到测量点的距离Rn项是已知的。测量中得到的相位差是2路信号间的相位差,因此在计算中需要相邻2路相减得到信号间相位差的表达式,以第1、2路间的相位差为例,根据式(5)得到:
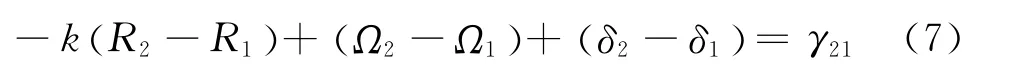
式中:R已知;γ为在测量点测得的1、2路信号的相位差。
令β21=Ω2-Ω1,表示得到的两阵元间方向图函数的相位差,即两阵元间所有相位差的积累得到的和值,再令Dmn=Rm-Rn,Δmn=δm-δn,得到:

由此可以求得各βmn,即得到各阵元间所有相位差异,再加上前面幅度值Cn,即得到阵元的幅度差异和阵元间的相位差异。
4 仿真与误差分析
对本系统进行仿真,先给定天线阵的参数,包括增益、激励电流、位置坐标、互耦系数矩阵等,另外给出测量点的位置。在该位置对理论上的测量值进行计算得到理论值,再将引入测量误差的参数进行计算得到实际值。将理论值和实际值相比较,得到测量误差对天线阵幅相误差测量计算的影响大小。
4.1 等效点源阵参数与测量仿真
首先以天线中心为坐标原点,根据图1给定8个点源的坐标如表1所示。
电波的工作频率为300 MHz,等效点源间的距离为0.6λ,设单个单元的输入功率为1 k W。天线的互耦系数矩阵如下表,其中前面的数值表示幅度,后面的数值表示复数值的角度值。其中各单元的自阻抗都是相等的,有Zmn=Znm。

表1 等效点源的位置坐标

表2 天线阵的互耦系数(其中上面数值表示复数值的幅度,下面数值表示复数值的角度)
天线阵对准的目标点为 (0,100 00cos15°,10 000sin15°),在天线的最大方向上。
给出这次测量点的位置坐标为A=[243.10,1378.73,246.86]。
因此,在A点得到的幅度测量值和相位差值如表3所示。

表3 在A点测量得到的幅度值很相位差值
由测量得到的相位和阵元的精确坐标值可以计算出各阵元间的相位差。可以看到,即使是在互耦影响较小的情况下,阵元间的互耦对天线传播的相位影响也是较大的。
4.2 带误差参数的仿真与分析
4.2.1 定位点源的位置误差对测量值的影响
在空间功率合成中,对于同一天线阵来说,相位差异是影响合成效率的主要因素。而对定位点源进行测量时引入的位置误差将影响到各阵元到测量点的波程,进而对相位产生影响。
这里考虑定位点源的位置误差时会有2个部分产生的误差:等效为点源时的误差和定位产生的误差。设位置测量的精度为±0.05 m,误差满足均匀分布下面对误差进行分析。
设8个等效点源的实际位置如表1所示,对每个点源加误差得到新的坐标值和与原坐标值的差值如表4所示。
在远场点A(243.10,1 378.73,246.86)得到的幅度不变,而相位前后变化如表5所示。
由测量可以知道:(1)在测量阵元位置时产生的误差只影响了相位的计算,这是因为瞄准点的初始相位的计算需要各阵元的坐标进行计算;(2)幅度计算值取各路信号的模,所以在相位差不同时幅度值是相等的。
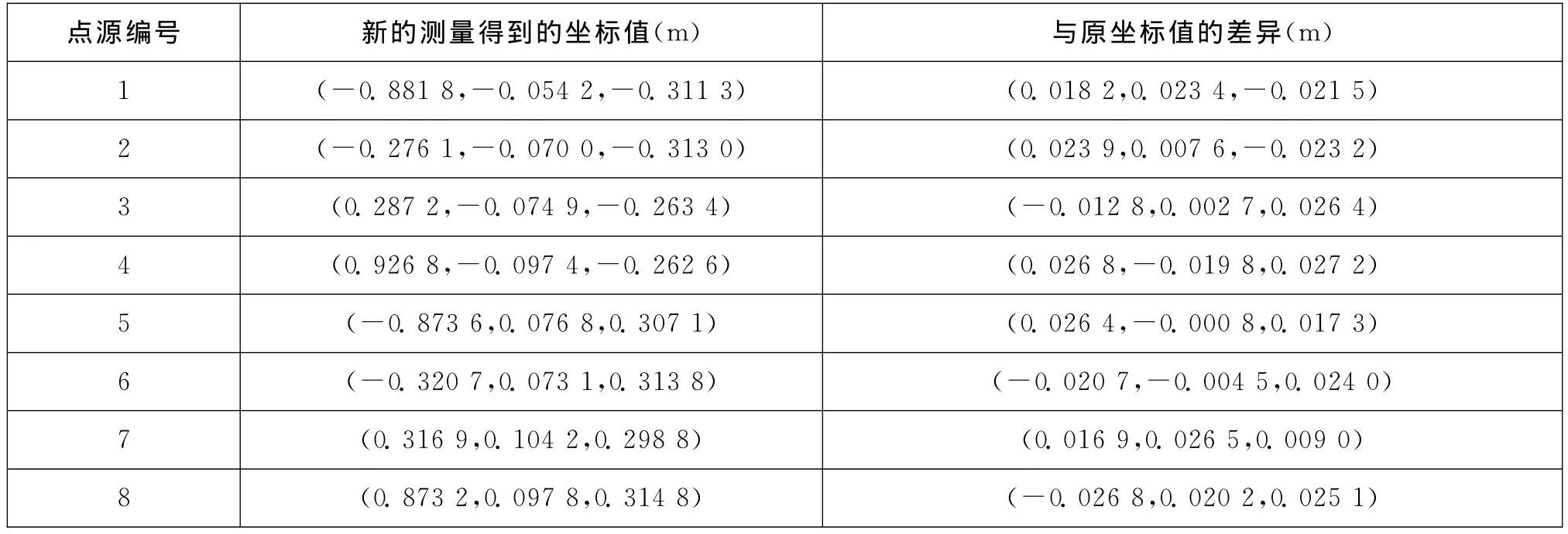
表4 存在误差时点源阵的位置坐标

表5 加入误差后相位差异测量的变化
另外,对以上的值进行10 000次均匀分布取值,得到第2路相对于第1路的相位差的分布如下:最大的相位偏差为24.238 1°,而当误差范围控制在x~U(-0.01,0.01) 时,最 大 的 相 位 偏 差 为4.901 4°。
4.2.2 测量点的定位误差对测量值的影响
测量点的定位误差范围与前面测量点源位置相近,此时满足均匀分布,得到测量点A的 新 坐 标 为 (243.081 6,1 378.716 3,246.839 5)。以该点来计算相位阵元间的相位差异并将其与实际值比较,如表6所示。
可以看出,测量点的定位误差对测量相位差值的影响要比等效点源的定位误差对阵元间相位差值的影响小得多。
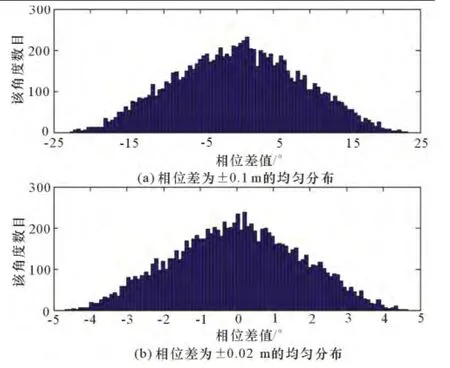
图3 仿真10 000次得到的第1、2路之间的相位差分布

表6 测量点的定位误差对相位差测量的影响
5 结束语
本文提出了一种新的对数周期天线阵元间幅相误差的求解方法,先将天线阵等效为一个无互耦的有方向性的点源阵,使用多路CDMA信号从各天线阵元发送出去,在远场使用CDMA信号接收机对不同信号进行解调,测量出不同信号间的相位差异和各路信号的幅度,进而区分出各路信号得到各阵元间的幅相误差。本文还给出了定位误差对计算结果的影响,结果表明测量方法是可行的,具有实用价值。
[1]齐亚平,朱林芳.短波多站空间功率合成通信干扰技术研究[J].电子对抗,2000(3):16-25.
[2]邓朝平,候德亭,周东方,等.密集阵高功率微波空间功率合成[J].强激光与粒子束,2013,25(2):436-439.
[3]耿京朝,牛传峰,毛贵海.双极化对数周期阵列天线[J].电波科学学报,2003,18(2):228-231.
[4]尚军平.相控阵天线快速测量与校准技术研究[D].西安:西安电子科技大学,2010.
[5]王健.多波束天线通道幅相误差的自校正算法[J].计算机测量与控制,2010,18(1):211-213.
[6]丁晓磊,王建,林昌禄.对数周期偶极子天线相位中心的分析和计算[J].电子学报,2003,31(9):1375-1377.
[7]丁晓磊,王建,林昌禄.对数周期偶极天线的一种新的分析方法[J].系统工程与电子技术,2002,24(5):16-19.
[8]丁晓磊.对数周期偶极天线扇形阵的特性分析及其软件实现[D].成都:电子科技大学,2002.
[9]吴世龙.短波对数周期天线及其阵列的方向性[J].舰船电子工程,2004,24(4):95-98.
[10]杨国英,赵福玲.对数周期偶极子天线阵的互耦分析[J].现代电子技术,2013,36(11):85-88.
[11]章宇兵,张浩,廖桂生.任意分散布阵短波通信干扰机空间功率合成技术[J].西安电子科技大学学报(自然科学版),2006,33(1):150-154.
