基于混沌时序最小二乘支持向量机的汽油机瞬态空燃比预测模型研究
2015-04-25徐东辉李岳林雷鸣何剑锋吴钢解福泉
徐东辉,李岳林,雷鸣,何剑锋,吴钢,解福泉,3
(1.宜春学院物理科学与工程技术学院,江西 宜春 336000;2.长沙理工大学汽车与机械工程学院,湖南 长沙 410076; 3.河南交通职业技术学院,河南 郑州 450005)
基于混沌时序最小二乘支持向量机的汽油机瞬态空燃比预测模型研究
徐东辉1,李岳林2,雷鸣1,何剑锋1,吴钢2,解福泉2,3
(1.宜春学院物理科学与工程技术学院,江西 宜春 336000;2.长沙理工大学汽车与机械工程学院,湖南 长沙 410076; 3.河南交通职业技术学院,河南 郑州 450005)
针对由氧传感器构成的瞬态空燃比反馈控制系统无法满足实时性要求的问题,提出了基于混沌时序最小二乘支持向量机(LS-SVM)的瞬态空燃比预测模型。对试验采集到的一维空燃比数据利用相空间重构技术构造多维空间数据,恢复空燃比时间序列的多维非线性特性,然后采用LS-SVM对重构后的数据进行训练及预测,得出预测结果。仿真结果表明:与Elman神经网络预测模型及前馈BP神经网络预测模型相比较,混沌时序LS-SVM预测模型具有更强的非线性预测能力,能够有效地提高瞬态空燃比的预测精度。
空燃比; 相空间重构; 瞬态工况; 支持向量机; 预测模型
目前,国内外对汽油机瞬态空燃比的控制大多采用前馈控制方法,但前馈控制方法无法对控制器之后的系统偏差进行修正,因此其控制精度仍然受到限制[1-2]。采用基于宽域氧传感器(或空燃比传感器)的空燃比反馈控制方法,由于氧传感器反馈信号存在延时,这会导致常规空燃比反馈控制存在时滞现象,且该反馈控制方法仅是对燃烧之后检测到的数据进行反馈,无法对燃烧之前的系统偏差进行及时有效修正,满足不了控制系统实时性要求,尤其在瞬态工况下,空燃比明显偏离理论值。就控制策略本身而言,反馈控制方法优于前馈控制,而要将反馈控制方法成功应用于空燃比控制中,就必须解决氧传感器反馈信号的时滞等诸多问题[3-5]。因此,对汽油机瞬态空燃比进行准确的提前预测将有利于增强控制系统的实时性,提高瞬态空燃比的控制精度。
近年来,内燃机行业的许多学者对空燃比的预测进行了深入研究,并提出了许多预测方法。侯志祥[6]等提出一种基于Elman神经网络的空燃比多步预测模型,试验表明该模型具有较高的预测精度;周能辉[7]等采用神经网络预测模型对汽油HCCI发动机的空燃比进行控制;吴义虎[8]等利用BP神经网络提出了一种基于神经网络的空燃比多步预测控制策略。虽然以上空燃比预测控制精度都得到了提高,但是神经网络采用经验风险最小化准则,训练过程中存在过拟合问题,导致其泛化能力下降,影响神经网络能力预测,其预测精度不能达到满意效果,同时也存收敛速度慢、容易陷入局部极小点等缺点。最小二乘支持向量机(LS-SVM)遵循结构风险最小化原则,能有效地解决神经网络的过拟合、易陷入局部极小值和泛化能力差等缺陷,因此,本研究建立一种瞬态空燃比的混沌时序LS-SVM预测模型,目的是对瞬态空燃比进行提前预测,解决氧传感器反馈信号存在延时等诸多的问题,提高瞬态空燃比控制精度及实时性,使反馈控制策略成功地运用于空燃比控制中。
1 瞬态空燃比混沌时序分析
Packard和Takens提出的相空间重构理论[9-10]是把具有混沌特性的时间序列重构成一种低阶非线性动力学系统,从而近似恢复原有系统的混沌吸引子。发动机是一个非线性动力学系统,瞬态空燃比是燃油与空气的混合体,具有多维非线性特性,因此可以把瞬态空燃比的预测问题转化为相空间里的一个短演化过程来进行讨论,也为瞬态空燃比混沌时间序列预测研究提供了可靠的前提条件[11]。
设汽油机瞬态空燃比的时间序列为{x(ti)}:
x(ti)=x(t0+nΔt)(i=1,2,3,…n)。
(1)
式中:t0为初始时间;Δt为采样时间间隔。
取一个合适的延滞时间τ和嵌入维数m,将原有时间序列x(ti)延拓成m维相空间的一个相型分布,即
x′(ti)={x(ti),x(ti+τ),x(ti+
2τ),…x(ti+(m-1)τ)}。
(2)
式中:τ=kΔt为延滞时间;k为整数。
本研究采用文献[12]所述的C-C方法求得τ=2,τw=14,所以时间延迟为2d,相空间重构的嵌入维数m=8。因此,由τ=2,m=8,计算得到最大Lyapunov指数0.005 7,稍大于0,表明瞬态空燃比时间序列具有混沌特性,因此可对其作短期预测。
2 最小二乘支持向量机(LS-SVM)算法
最小二乘支持向量机是SVM的变形,建立在结构风险最小化和统计学习理论基础之上,具有更高的泛化能力,且具有唯一性解,有效地避免了陷入局部最优的特点[13]。
假设汽油机瞬态工况空燃比的训练样本集为{(xi,yi)},i=1,2,…n,xi和yi分别表示空燃比支持向量机预测模型训练样本的输入和输出,利用非线性映射函数φ(·)将样本映射到高维特征空间,在高维特征空间上进行线性回归,即
f(x)=wTφ(x)+b。
(3)
式中:b为偏置量;w为权值向量。
根据结构风险最小化原则,式(3)问题求解LS-SVM回归模型
s.t.yi=wTφ(x)+b+ζi。
(4)
式中:γ为正则化参数。
通过引入拉格朗日乘子将约束优化问题转变为无约束对偶空间优化问题,即
(5)
式中:αi为拉格朗日乘子,优化条件为
(6)
可得:
wTφ(xi)+b+ζi-yi=0。
(7)
根据Mereer条件K(xi,xj)=φ(xi)Tφ(xj),建立汽油机空燃比支持向量机预测模型:
(8)
一般情况下,径向基核函数性能要优于其他核函数,因此本研究选择其作为LS-SVM核函数,径向基核函数表达式为
(9)
式中:xi为训练样本数据;xj为核函数的中心;σ为核函数的宽度参数。
最后得到LS-SVM空燃比预测模型:
(10)
由于超参数γ和核参数σ2将影响LS-SVM的预测精度及泛化能力,因此本研究采用文献[14]中的混沌优化方法,利用Logistic映射混沌模型对径向基核函数中的γ,σ2两个参数取混沌变量使其快速达到全局最优,有效地降低了最小二乘支持向量机的预测误差并提高了它的泛化能力。
3 混沌时序LS-SVM预测模型建立
本研究通过对汽油机瞬态工况空燃比的混沌非线性特性进行分析,对采集的原始数据进行相空间重构,采用建立的LS-SVM模型对重构后的数据进行预测[15-17]。混沌时序LS-SVM预测模型见图 1。
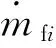
混沌时序LS-SVM模型预测原理如下:首先对瞬态空燃比数据进行相空间重构,然后利用重构后的数据对LS-SVM预测模型进行训练,得到下一时刻支持向量机的一步预测模型:
(11)
式中:m为嵌入维数;τ为延迟时间;Xt=(xt,xt+τ,xt+2τ,…xt+(m-1)τ)。
对于相空间重构的第t+1点,有
(12)
再由式(11)得到对t+2点的预报:
(13)
于是得到第p步的混沌时序LS-SVM预测模型:
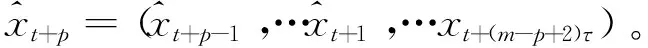
4 试验验证及误差分析
4.1 试验仿真
试验发动机选为某4缸电喷汽油机, 标定功率73.5 kW,标定功率转速3 800 r/min,排量2.84 L,压缩比7.8,怠速转速750 r/min,采用CW260电涡流测功器,按上述方法建立空燃比数学模型。根据香农采样定律,本试验数据采集方案设置采样频率为100 Hz,即采样时间为0.01 s。由于发动机过渡工况情况复杂,因此,在节气门全程范围内采用加速、减速两个阶段进行试验,同时采集节气门开度信号、进气管压信号、发动机转速信号、喷油脉冲宽度及空燃比信号等。发动机加速试验方案:在1 s,2 s,3 s,4 s和5 s内以不同速度分别使节气门开度由怠速位置开启至85%开度,试验测试时间设置为5 s,共采集5×500组空燃比试验数据。发动机减速试验方案:在1 s,2 s,3 s,4 s和5 s内以不同速度分别使节气门开度由85%开度减速至怠速位置,试验测试时间设置为5 s,共采集5×500组空燃比试验数据。
上述分析已经证明了可对汽油机瞬态空燃比作短期预测,因此对采集的试验标定值进行归一化处理,并进行相空间重构,得8×500组数据,任意取6×500组数据作为混沌时序LS-SVM预测模型的训练样本,2×500组数据作为预测模型的检验样本。在试验仿真时充分考虑节气门开度信号、进气管压信号、发动机转速信号、喷油脉冲宽度等信号对空燃比预测的影响。加速工况混沌时序LS-SVM预测曲线见图2,减速工况混沌时序LS-SVM预测曲线见图3。
4.2 误差分析与比较
本研究采用平均绝对误差(μMAE)、均方根误差(μRMSE)及平均相对误差(μMRE)作为定量估测各预测模型准确性的性能指标,其定义如下:
(15)
(16)
(17)
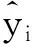
加速工况空燃比预测模型误差分析与比较见表1,减速工况空燃比预测模型误差分析与比较见表2,加速工况混沌时序LS-SVM预测结果与Elman神经网络及前馈BP神经网络预测结果的比较见图4,减速工况混沌时序LS-SVM预测结果与Elman神经网络及前馈BP神经网络预测结果的比较见图5。
通过误差分析与比较可知,混沌时序LS-SVM预测模型的平均相对误差比Elman神经网络模型高了约7%,比前馈BP神经网络高了约8%, 混沌时序LS-SVM预测模型的均方根误差比Elman神经网络模型提高了0.1,比前馈BP神经网络提高了0.15。由此可见,混沌时序LS-SVM预测模型有效地克服了神经网络的过拟合、易陷入局部极小值和泛化能力差的缺陷,预测精度优于Elman神经网络预测模型及前馈BP神经网络模型,且收敛速度更快。
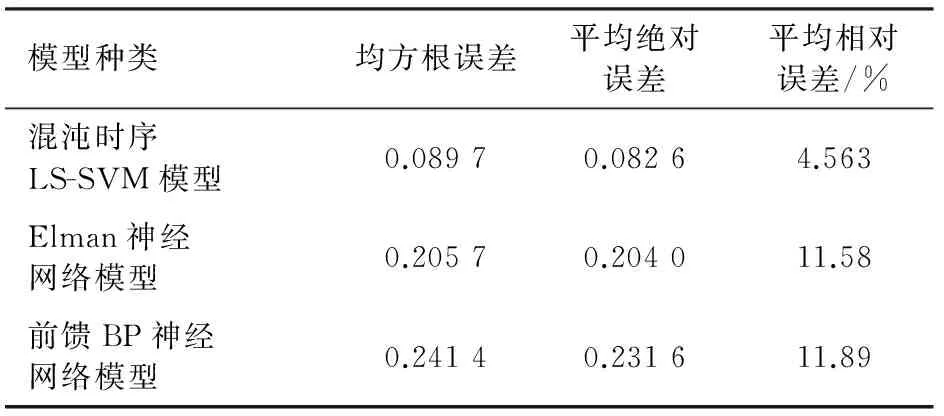
表1 加速工况空燃比预测模型误差分析与比较
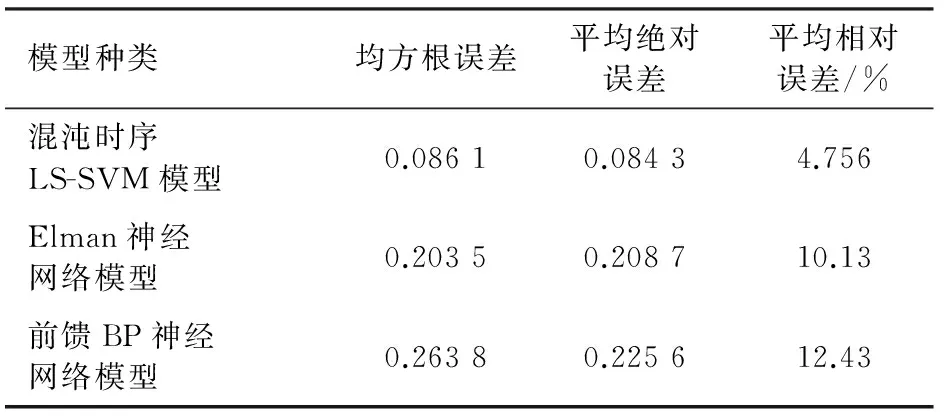
表2 减速工况空燃比预测模型误差分析与比较
4.3 台架试验验证
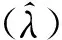
由图7至图10及表3可知,在2 000 r/min瞬态工况下,空燃比前馈控制误差为5.26%,而LS-SVM预测模型反馈控制误差为2.26%;当转速在2 500 r/min时,空燃比前馈控制误差为6.51%,而反馈控制误差为3.11%。从而进一步证明了LS-SVM预测模型能对控制器之后的系统偏差进行及时修正,控制系统的实时性得到了提高,瞬态空燃比得到了有效控制。

表3 台架试验各转速点误差统计
5 结束语
针对汽油机瞬态空燃比的多维非线性混沌特性,提出了混沌时序LS-SVM预测模型,经试验仿真证明,该模型的预测精度优于Elman神经网络模型及前馈BP神经网络模型,表明了混沌时序LS-SVM预测模型具有更强的非线性预测、学习及泛化能力。台架试验也验证了混沌时序LS-SVM预测模型的有效性,进一步说明了该预测模型有较高的工程实际应用价值。
[1] 石屹然,田彦涛,张立,等.SI发动机空燃比联合非线性模型预测控制[J].吉林大学学报:工学版,2014,44 (3):726-734.
[2] 胡春明,张基伟,刘娜.基于遗传算法参数辨识的汽油机各缸空燃比均匀性控制[J].内燃机工程,2013,34(6):13-18.
[3] 刘一鸣,花志远,陈永全.广义预测控制算法在发动机空燃比控制中的应用[J].汽车工程,2013,35(5):403-407.
[4] 孟嗣宗,郭少平,张文海.发动机精确空燃比控制方法的研究[J].内燃机工程,1999,20(2):70-75.
[5] Zhai Y J,Yu D L.Neural networkmodel-based automo-tive engine air/fuel ratio control and robustness evaluation[J].Engineering Applications of Artificial Intelligence,2009,22(2):171-180.
[6] 侯志祥,申群太,吴义虎,等.基于Elman神经网络的汽油机过渡工况空燃比多步预测模型[J].中南大学学报:自然科学版,2006,37(5):981-985.
[7] 周能辉,谢辉,赵华,等.基于神经网络的汽油HCCI发动机空燃比控制策略[J].农业机械学报,2009,6(40):2-5.
[8] 吴义虎,侯志祥,申群太.车用汽油机过渡工况空燃比的神经网络多步预测控制策略[J].燃烧科学与技术,2008,14(1):11-15.
[9] 张学工.关于统计学习理论与支持向量机[J].自动化学报,2000,26(1):32-43.
[10] Takens F.On the numerical determination of the dimension of an attractor[J].Dy namical systems and Bifurcations Lecture Notes in Mathematics,1985,1125:99-106.
[11] Grassberger P,Procaccial.Measuring the strangeness of strange attractors[J].Physica D,1983,9:189-208.
[12] 吕金虎,占勇,陆君安.电力系统短期负荷预测的非线性混沌改进模型[J].中国电机工程学报,2000,20(12):80-83.
[13] Vapnik V N.The Nature of Statistcal Learning Theory[M].New York:Springer-Verlag,1995.
[14] 霍明,罗滇生,何井龙,等.短期负荷预测中SVM参数选取的混沌优化方法[J].电力系统及其自动化学报,2009,21(5):124-128.
[15] Jun-li Zhang,Guo Zhou,Yong-quan Zhou.A New Artificial Glowworm Swarm Optimization Algorithm Based on Chaos Method[J].uantitative Logic and Soft Computing,2010,82:683-693.
[16] 何俊学.基于支持向量机的软件可靠性模型研究[D].兰州:兰州理工大学,2009.
[17] Wong P K,Wong H C,Vong C M.Online time-sequence incremental and decremental least squares supportvector machines for engine air-ratio prediction[J].InternationalJournal of Engine Research, 2011,13(1):28-40.
[编辑:袁晓燕]
Prediction Model of Transient Air-fuel Ratio for Gasoline Engine Based on Chaos Least Square Support Vector Machine
XU Dong-hui1, LI Yue-lin2, LEI Ming1, HE Jian-feng1, WU Gang2, XIE Fu-quan2,3
(1.Physical Science and Engineering College of Yichun University, Yichun 336000, China;2.School of Automotive and Mechanical Engineering,Changsha University of Science and Technology, Changsha 410076, China;3.Henan Communications Vocational and Technical College, Zhengzhou 450005, China)
For the problem that the feedback control system of transient air-fuel ratio with oxygen sensor could not realize the real-time demand, the prediction model of chaos least square support vector machine was put forward.The multi-dimensional space data were constructed with the collected test data, the multi-dimensional non-linear characteristics of air-fuel ratio time series were restored, the reconstructed data were trained with LS-SVM and the prediction results were acquired.The results show that the chaos LS-SVM prediction model has the non-linear prediction ability and can improve the prediction accuracy of air-fuel ratio effectively compared with the Elman and BP network model.
air-fuel ratio; phase space reconstruction; transient condition; support vector machine (SVM); prediction model
2014-09-29;
2015-02-01
国家自然科学基金项目(51406017);国家自然科学基金项目(51176014);高等学校博士学科点专项科研基金项目(20104316110002);河南省交通厅科研项目(2012PII10);工程车辆轻量化与可靠性技术湖南省高校重点实验室基金资助项目(2013kfjj02)
徐东辉(1978—),男,博士,主要研究方向为汽车节能减排与新能源技术等;xyh22810417@163.com。
10.3969/j.issn.1001-2222.2015.02.003
TK411.7
B
1001-2222(2015)02-0013-05
