基于相关性理论确定影响高速公路路基工程量的技术指标

■林 果

（福建省交通工程造价管理站，福州 350001）

0 引言

高速公路工程建设项目相对于一般土建项目而言，是一个周期长、投资大、技术标准高、受地质和天气影响大、较为复杂的生产消费过程，期间需要消耗大量的人工、材料、机械及生活资料。据相关统计，福建省高速公路每公里需消耗水泥14000t、 钢材2500t、 沥青550t、 矿石料6 万m3、 油料600t、 用地需求量每公里100 亩。而在公路工程项目建设的整个投资过程中，设计成本控制尤为重要。路基工程量是高速公路工程量的重要组成部分，路基工程主要工程量包括有土石方、防护工程、排水工程。在设计阶段，相似地形下路基工程量受到各种技术指标的影响， 不同的设计技术指标将直接影响工程量的大小。

以福建省已修建的高速公路为统计数据，统计区段内的路基典型工程数量及技术指标；技术指标统计为：路线增长系数、最大直线长度、最大纵坡长度、最大纵坡、综合平曲线半径、综合竖曲线半径、平曲线比例、竖曲线比例。在福建省已修建完成的高速公路中微丘地形下四车道设计时速为80km/h 的高速公路样本数最多，采用该样本作为数据进行分析。

1 相关性分析

1.1 分析理论

相关性分析[1]（Correlation analysis）是指对两个或多个具备相关性的变量元素进行分析， 从而衡量两个变量因素的相关密切程度。 相关性的元素之间需要存在一定的联系或者概率才可以进行相关性分析。 相关关系反映出变量之间虽然相互影响，具有依存关系，但彼此之间是不能一一对应的。

相关性分析其实就是观察一下各个指标的相关程度。 一般来说相关性越是高， 做主成分分析就越是成功。评价相关性的方法就是相关系数，由于是多变量的判定，则引出相关系数矩阵。相关分析所用的指标是相关系数及对应的显著性水平。相关系数r 是反映两变量之间相关关系密切程度的统计量、变量之间的线性相关程度，其取值在-1～1 之间；显著水平是相关系数的可靠程度，其取值在0～1 之间。具体说明如下：

（1） 当0＜|r|＜1 时， 表明变量之间存在一定的线性相关关系。若r＞0，表明变量之间为正相关；若r＜0，表明变量之间为负相关。

（2）当r=0 时，表明变量之间无线性相关关系，但两者间依然可能可以存在非线性的相关关系。

（3）对于相关性检验结果一般遵循的原则如下：

①相关系数满足：0＜|r|＜1；

②Sig.（双侧显著性水平值）＜α（预定的显著性水平）；

SPSS 软件[2]共提供了3 种相关性检验的方法，分别是Pearson（皮尔逊） 法、 Kendall（Kendall's tau-b）（肯德尔） 法及Spearman（Spearman's rho） （斯皮尔曼）法，3 种方法的使用条件有所不同[3]，具体如下：

Pearson 相关系数法一般要求变量是正态分布， 没有奇异值影响。由于统计数据中设计技术指标大多数并不服从正态分布，因此，在本文中并未采用Pearson 相关系数进行相关性检验。

Kendall 法要求每个评价者都能对N 件事物 （或作品）好坏、优劣、喜好、大小、高低等排出一个等级顺序，即大致能够对每一个x 对每一个y 的影响排序，这一点是较为困难的， 因此， 在本文中并未采用Kendall（Kendall's tau-b）相关系数进行相关性检验。

由于Spearman 对原始变量的分布不作要求， 属于非参数统计方法，适用范围较广。因此，在本文最终采用Spearman（Spearman's rho）相关系数进行相关性检验。

1.2 Spearman（Spearman's rho）相关系数法

又称秩相关系数、 等级相关系数， 或顺序相关系数[3]，对不服从正态分布的、一侧开口、总体分布类型未知等不符合使用积矩相关系数来描述关联性 （即不采用Pearson 相关系数法）的数据较为适用。Spearman 法采用秩相关（也称等级相关） （rank correlation），来描述两个变量之间的关联程度与方向， 其计算方法与Pearson法公式形式很相似，但有所不同，如公式(1)所示。

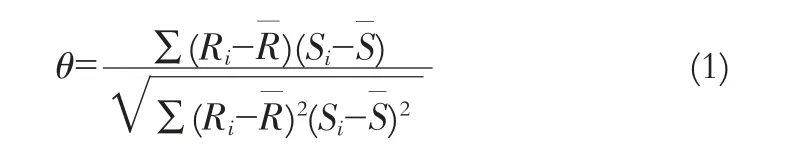
式中，Ri（或Si）——第i 个x（或y）值的秩；

1.3 工程量与技术指标样本合理区间

由于高速公路工程项目具有线长、量大、单一性特殊性明显等特点， 为了统计样本更具代表性， 需进行“典型工程量”合理区间的确定，剔除统计过程中不合理的样本。高速公路微丘地区140 个样本，将样本中每个 “典型工程量”进行排序，作出其散点图，由点构成的曲线越接近水平的直线就说明这一区域集中程度越高，反之越低；点与点之间越紧密说明这一区间连续性越好，技术指标集中程度越高，反之越小。故计算出点与点间的相差度a 就能知道点与点的连续性，相差度a由以下公式进行计算。

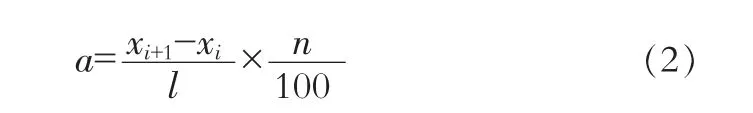
式中，xi+1、xi——表示某一技术指标相邻两点的指标；

l——表示该技术指标的样本区间长度；

n——表示样本的总数。

由于统计分析可得，当样本数为100 时，相差度小于0.01 时， 表明相差度在合理范围内， 当相差度小于0.005 时，表明相差度比较小，样本集中程度比较明显，当相差度大于0.01 时，表明相差度不在合理范围内，集中程度较弱；当相差度大于0.05 时，表明相差度极度偏离合理范围内，相应的点应当予以剔除。结合上述理论可确定 “典型工程量”合理区间，计算出合理区间的范围（上限-下限）、合理区间的范围的比例以及合理区间内样本个数。高速公路微丘设计时速80km 工程量合理区间如下表1。区间范围结果如图1～图3 所示。

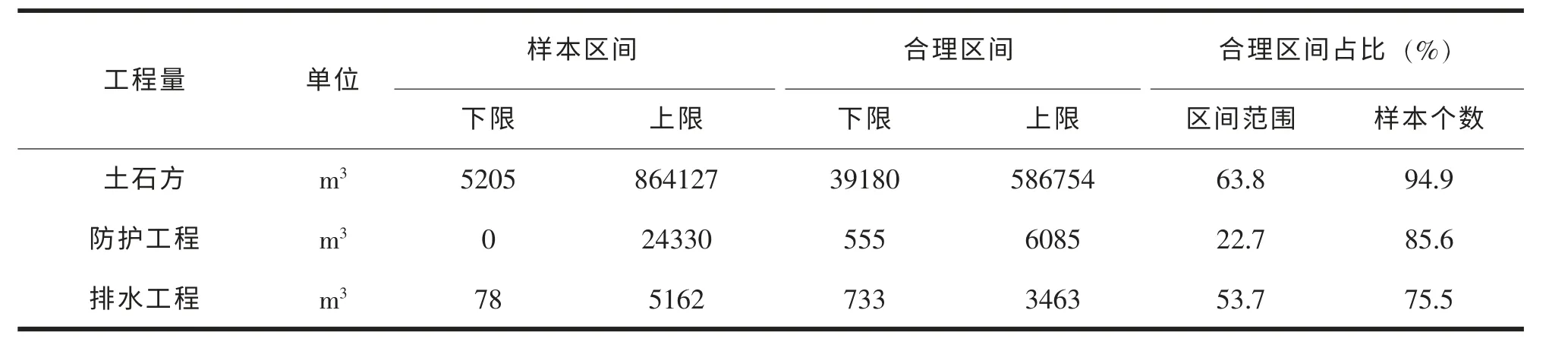
表1 微丘工程量合理区间表

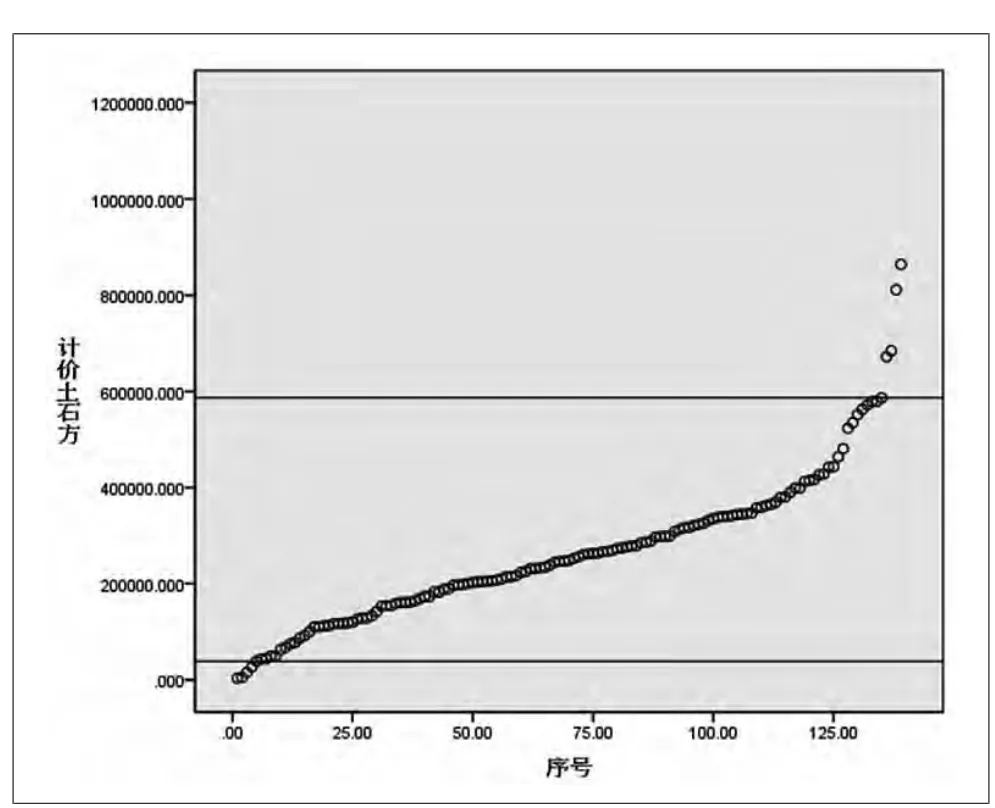
图1 计价土石方排序散点图

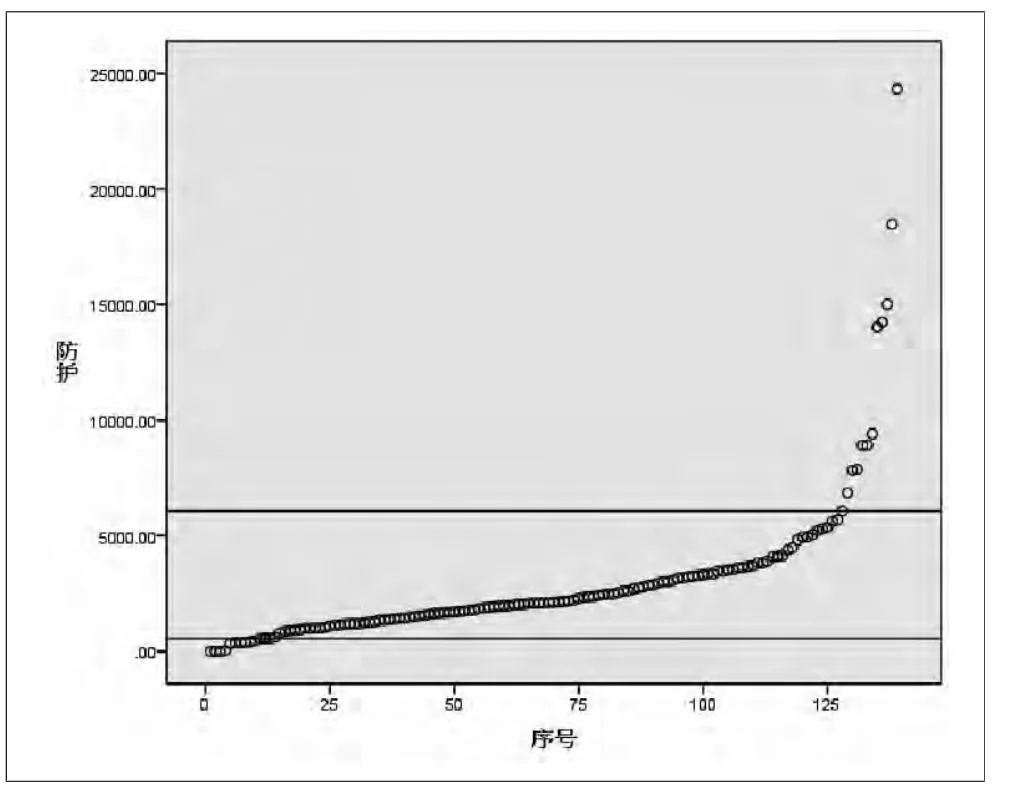
图2 防护工程排序散点图

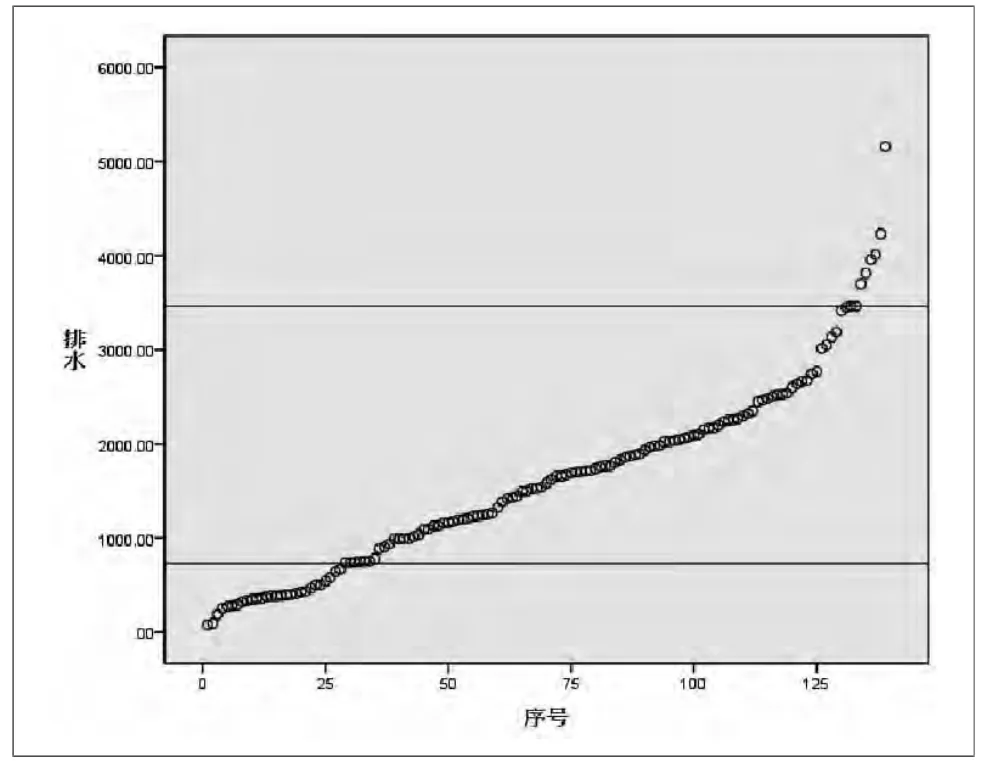
图3 排水工程排序散点图

对上述结果进行研究分析发现，在较小的区间内，包含了绝大多数的样本，这说明样本集中在一个较小的区域内，该区间能很好的反应样本集中的这一特性，能基本满足应用要求。即可确定为工程量的合理区间。

1.4 工程量与技术指标相关性分析

一般在进行相关性分析时， 通过两组数据之间的“相关系数”及 “显著性水平 （双侧）”2 项数值共同判断两者之间的相关关系。判定法则如下：

（1）通过相关系数的取值，比较相关系数值是否与1 较为接近，大致判定两组数据之间是否可能存在近似线性相关的关系。

（2）通过显著性水平 （Sig.）取值，判定 （1）中所得出的两组数据之间的相关关系是否值得信赖。在数学分析中，一般取0.05（双侧）为相关性分析的判定分界值，即当两组数据显著性值≤0.05 时，认为该两组数据具有显著的相关关系 （相关关系值得信赖）。

由于高速公路工程项目线长、点多、受地形、地质等各种因素交互影响，工程数量会因为实际情况的不同而产生一定偏差，因此在研究分析中，可以考虑一定程度上降低判别标准，本文将相关分析的显著性水平最大放宽值0.15（双侧）， 分析过程中共采用了0.01（双侧）、0.05（双侧）、0.10（双侧）、0.15（双侧），共4 档不同的显著性水平。将合理区间内 （见表1）样本 “路基典型工程量数据”三个指标与相应的 “设计技术指标数据”八个指标分别录入SPSS 软件，进行技术指标与工程量建立相关性分析。设计技术指标与标准路基典型工程量的相关分析情况如表2 所示。

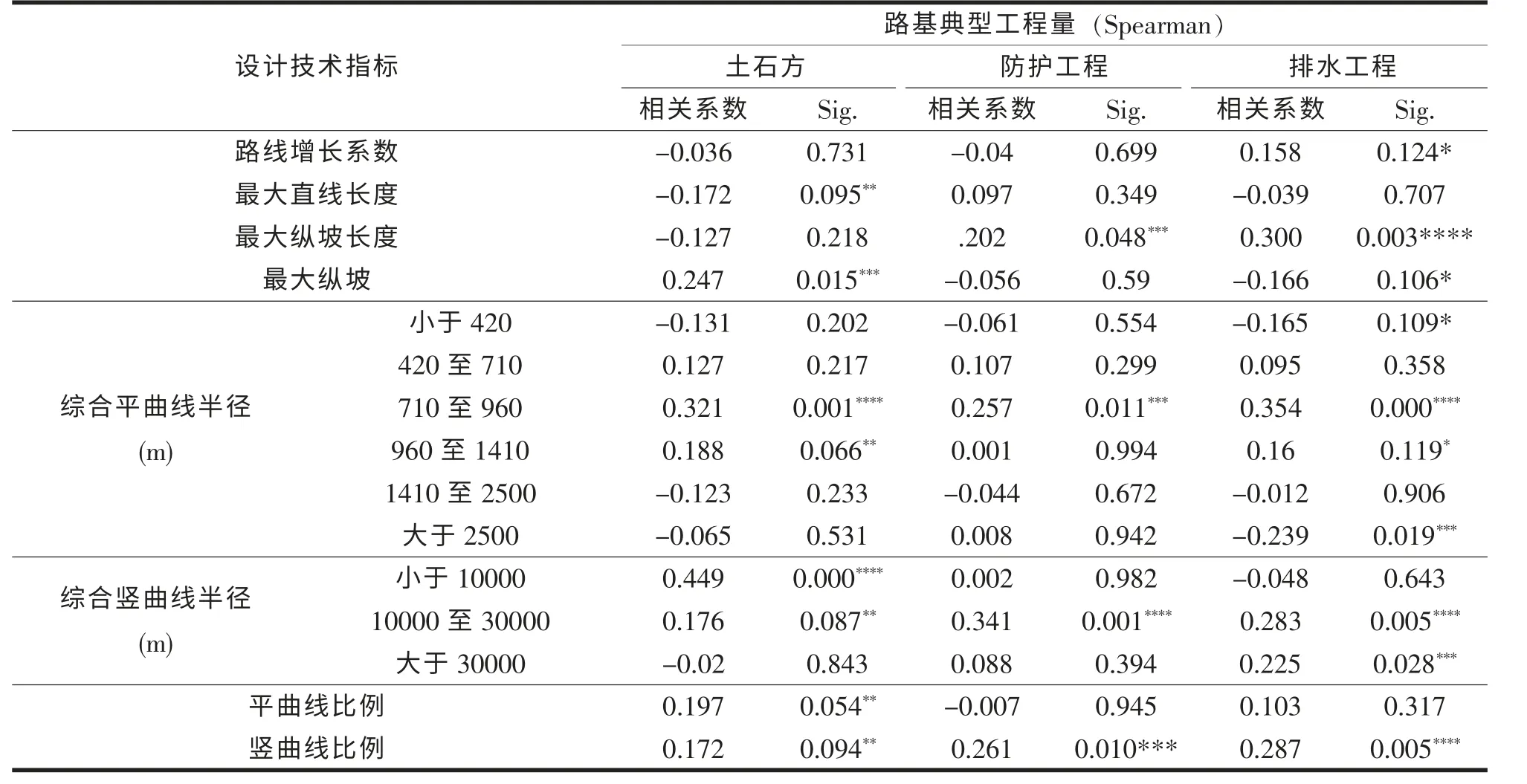
表2 设计技术指标与路基典型工程量的相关分析结果

由表2 可知：①与各项工程量具有显著相关关系的技术指标不止一个，即各项工程数量的多少取决于多个主要指标的共同制约；②各个与工程数量显著相关的技术指标的相关系数均较小 （<0.50），这些技术指标与相应工程数量之间的关系均为非线性关系。

2 相关性分析结果及应用

2.1 相关性分析结果

对表2 数据进行整理，将Spearman（Spearman's rho）相关系数进行相关性检验结果中，在0.01（双侧）、0.05（双侧）、0.10（双侧）、0.15（双侧）4 档不同的显著性水平条件下，具有显著相关关系的“设计技术指标”与“路基典型工程量”进行汇总，具体情况如表3 所示。

如果考虑到以上设计技术指标中归类，一定区间内平（竖）曲线半径个数统计值受制约影响因素较多可以合并， 因此， 将剩余指标列为各项路基典型工程量的“主要指标”，如表4 所示。

表3 设计技术指标与路基典型工程量的相关分析结果

表4 各路基工程量的主要指标汇总

在确定与 “路基典型工程量”具有显著相关关系的“设计技术指标”后，按照显著性水平由高到低 （Sig.值由小到大），对影响各项 “路基典型工程量”的 “设计技术指标”进行排序，排序靠前的 “设计技术指标”即为影响 “路基典型工程量”的 “主要指标”， “主要指标”的确定为后期建立 “路基典型工程量”与 “设计技术指标”中的“主要指标”间的关系奠定了基础。

2.2 应用实况

（1）构建预测模型

根据相关性分析表4 结果， 以0.05（双侧） 为例，各工程量对应相关性较显著的技术指标，其模型建立过程中以Yi-j表示第i 个工程表与第j 技术指标间的函数关系，具体情况如表5 所示，Y1、Y2、Y3分别表示工程量计价土石方、防护、排水。

表5 拟合模型因变量表

运用MATLAB 软件，录入微丘地形、设计速度为80km/h 条件下，各个样本的技术指标及工程数量统计值， 依据相关性分析结果： 对于土石方， 选取最大纵坡、综合平曲线半径及竖曲线半径为主要技术指标，对于防护工程和排水工程，选取最大纵坡长度、竖曲线长度、综合平曲线半径及竖曲线半径为主要技术指标，即自变量，通过MATLAB 拟合工具箱，分别确定拟合程度最高的一元函数模型。将Yij录入到spss 中进行二次拟合，得到综合模型。重复以上过程，进行多次尝试，找到拟合程度最好的模型。分别得出土石方工程、防护工程、排水工程与相关技术指标的关系函数。交通工程造价管理人员可以在优化技术指标时快速估算出路基工程量。也为造价管理部门的造价审查提供方便和科学依据。

（2）优化设计指标配置

从近年来设计情况看，总体上设计指标还存在配置不尽合理，仍有优化空间。因此，可以通过给出了不同置信区间内影响高速公路典型工程量的主要技术指标，加强对公路线形设计指标配置的剖析，达到减少工程数量，节省工程造价的目的。

3 小结

通过高速公路优化设计的应用表明，优化方案值得应用和推广，经过我省11 条高速公路应用的分析与统计，测设里程449.8km，初编概算438 亿元，节省费用29.14 亿元，取得明显的经济效果。

[1]王爱莲.统计学.第七章 相关与回归分析.第一节 相关分析.西安石油大学,经济管理学院.

[2]邓维斌，唐兴燕.SPSS 统计分析软件19（中文版）[M].电子工业出版社，2012.3.

[3]徐维超.相关系数研究综述[J].广东工业大学学报,2012(03).