一种永磁同步电机容错控制方法

焦山旺， 施火泉， 汤一林

(江南大学轻工过程先进控制教育部重点实验室，江苏无锡214122)

随着电力传动技术的发展，调速系统的安全性受到越来越多的关注［1］，并已成为用户选型时的重要技术指标。在欧洲，调速系统的安全性已成为行业的强制标准。变频调速系统能否在发生故障时准确进行故障诊断，并安全容错运行是变频调速系统安全性的重要组成部分。速度传感器是PMSM矢量控制系统中较脆弱的一环，当其出现接触不良或传感器断线故障时，会造成控制系统的飞车，损坏设备，甚至威胁到操作者的人身安全。因此，对速度传感器故障检测和容错控制技术的研究，具有非常重要的实用价值。速度传感器的故障检测方法通常可分为软件检测法和硬件检测法。软件法具有对各种速度传感器很好的适应性，近年来，许多学者对基于软件法的速度传感器故障检测进行了深入的研究。文献［2-5］将神经网络和模糊控制等智能算法应用到速度传感器故障的检测中。但由于软件检测需要占用较多的软件资源，且故障检测速度较慢。文献［6-7］通过硬件电路实现速度传感器的故障诊断，相对软件检测法，硬件检测法具有诊断速度快，不占用处理器资源等优点。微控制器可通过检测硬件电路的故障信号及时进行故障隔离，同时采取相应的补救措施。因此，文中采用模拟硬件检测法，进行故障的检测;在检测到速度传感器发生故障后，PMSM矢量控制系统自动平滑地切换到工作在无速度传感器状态下，从而实现速度传感器的容错控制。这样，控制系统在速度传感器无故障时可实现带速度传感器的矢量控制，具备很高的性能指标，在速度传感器发生故障后又可以安全容错运行，提高了系统的可靠性。

1 永磁同步电机矢量控制系统的设计

永磁同步电机矢量控制系统的设计在很多文献中都有详细说明，本实验采用id=0矢量控制方案，控制系统原理框架如图1所示。

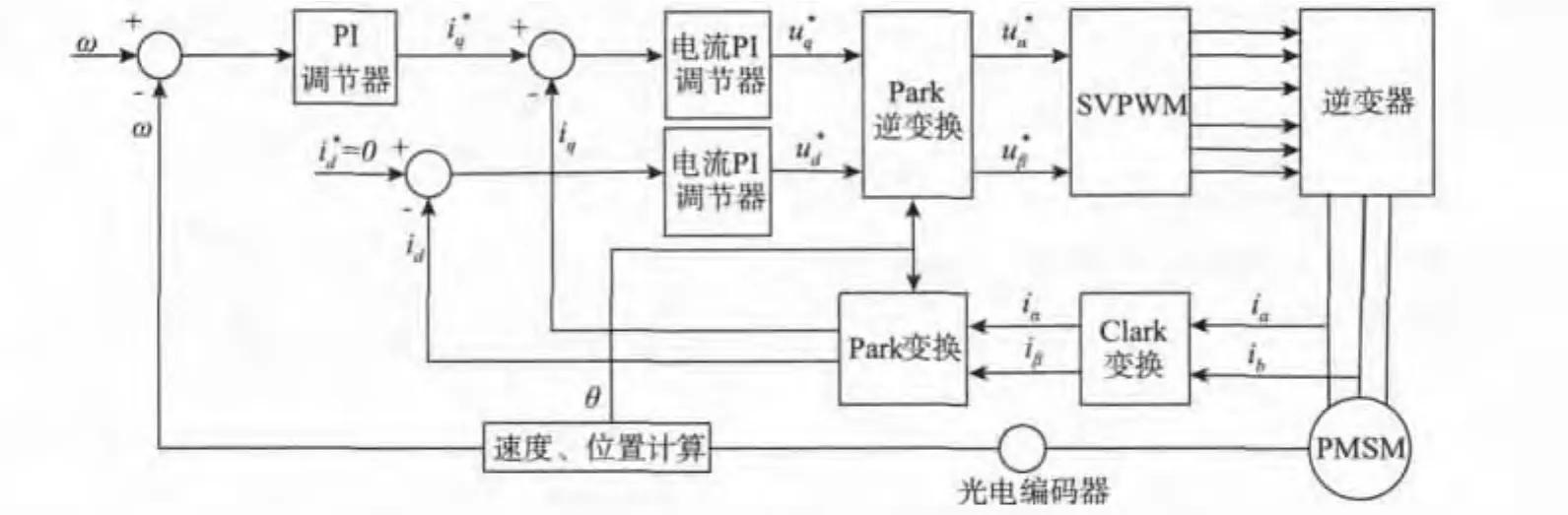
图1 系统控制原理框架Fig.1 Principle diagram of a control system

图1 中，ω*，ω分别为给定转速、和实际转速;分别为d轴和q轴电流的给定值;id，iq分别为d轴和q轴电流的实际值;分别为d轴和q轴电压的给定值。

按图1设计完成的永磁同步电机带速度传感器矢量控制系统具备较好的稳态性能和动态性能。系统在1 500 r/min给定转速下，带3 N·m的负载启动，电机转速及电流的波形如图2所示。

由电机的转速和电流响应可知，文中设计的带速度传感器的永磁同步电机矢量控制系统具有较好的稳态性能和动态性能。

2 无速度传感器矢量控制系统设计

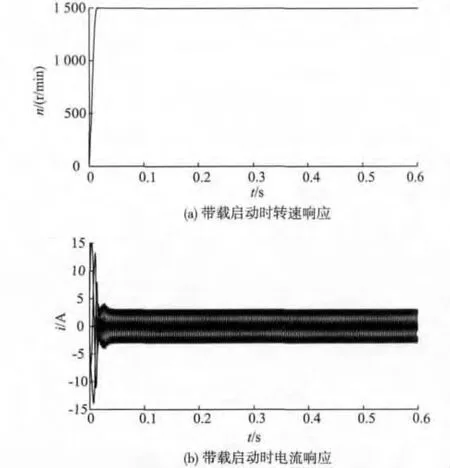
图2 带载启动时系统响应Fig.2 System response with load

2.1 滑模观测器设计

永磁同步电机(表贴式)定子侧采用三相对称绕组，转子为永磁体。其在两相静止坐标系下的数学模型为

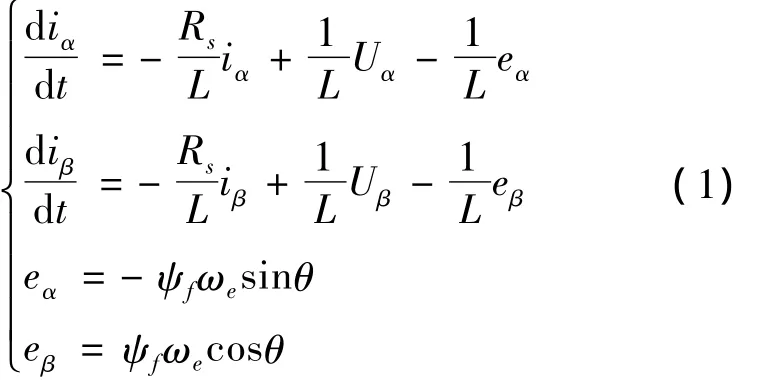
式中:Rs为定子电阻;L 为定子电感;iα，iβ，Uα，Uβ，eα，eβ分别为静止坐标系下的电流，电压和反电动势;ψf为转子磁链;θ为转子位置;ωe为转子电角速度。

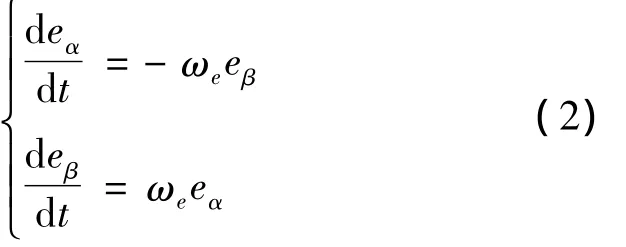
传统滑模观测器先根据滑模开关函数求出电机的反电势信号，然后计算出电机的转子位置信息。由于开关函数的不连续性，系统存在抖振，且反电动势是通过低通滤波器得到的。故通过滤波得到的反电势计算出的位置信息就会存在相位滞后，需要进行相位补偿，这在一定程度上就增加了系统的复杂性。因此，文中采用Sigmoid函数代替滑模开关函数的滑模观测器，其原理如图3所示。

图3 滑模观测器原理Fig.3 Diagram of a sliding mode observer

滑模观测器的数学模型为

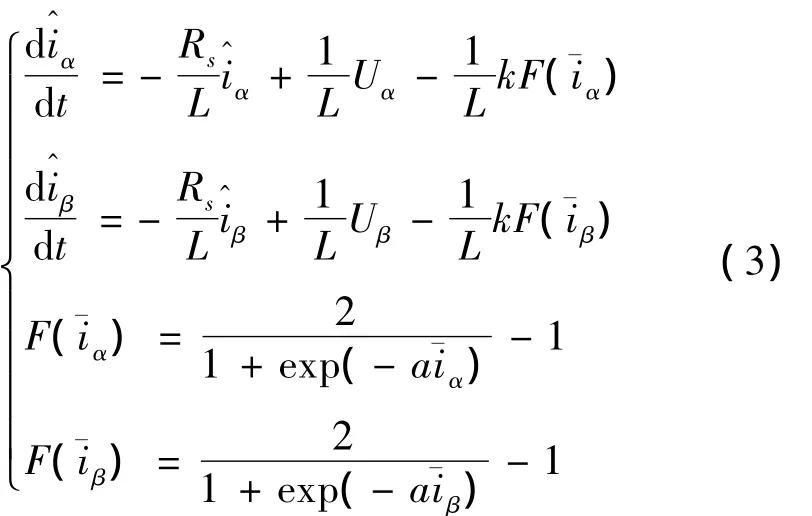
其中:a，k为大于零的常数，a决定S型函数的斜率，k决定滑模观测器的收敛速度;为电流估计值。

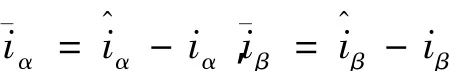
选取滑模面

同时构造Lyapunov函数

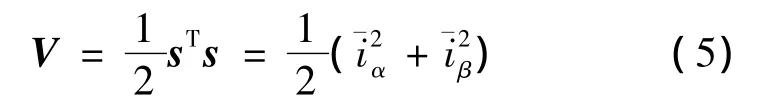
由式(1)、式(2)、式(3)和式(5)可得:

则由式(6)可知，只要k满足条件:

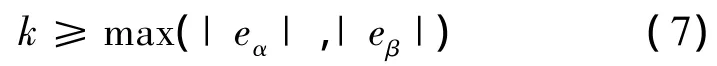
就能够保证滑模观测器收敛。k的值越大，滑模观测器收敛的速度越快，但过大的k值会造成严重的系统抖振。因此，系统必须在快速性和减小抖振之间寻找平衡，确定一个合适的k值。

2.2 锁相环的位置和速度估计

滑模观测器估算出的反电动势中包含了磁极角度的正余弦信息，一般都是利用反正切函数进行转子角度的计算［8］，需要通过查询反正切数值表获取角度值，因此会产生计算噪声，且当转角为90时，角度计算偏差较大［9］。为了提高系统的鲁棒性，应用锁相环估计转子速度和位置，图4为锁相环实现框图。其中:为反电动势中包含的转速信息为观测器估计出的转子位置。

图4 锁相环框架Fig.4 Diagram of PLL

文中设计的锁相环模型为

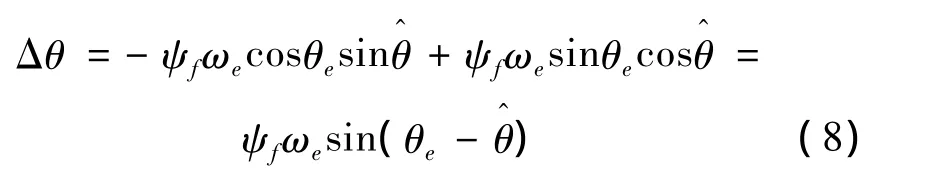
令 λ = ψfωe，则有

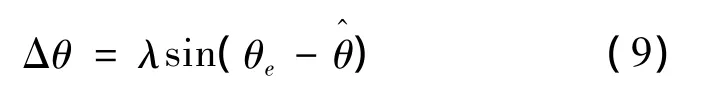
由式(9)可得如图5所示的简化锁相环系统。

图5 简化的锁相环系统Fig.5 Simplified block diagram of PLL

则锁相环系统的闭环传递函数为

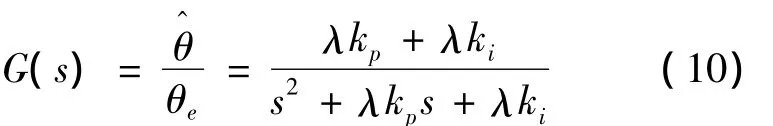
位置误差传递函数为

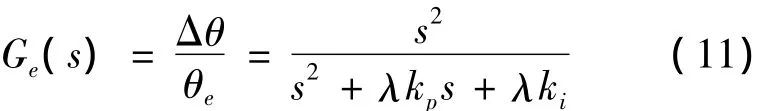
当转速不变时，θe近似为一个斜坡函数θe=ωet，因此锁相环系统估算位置的稳态误差为

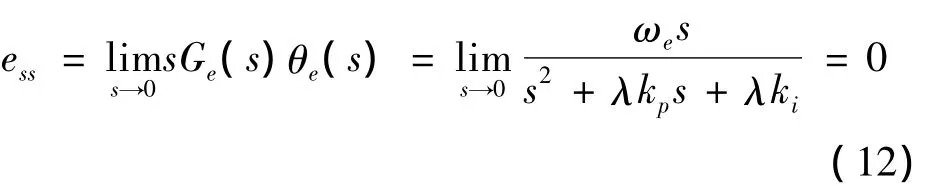
由此表明，设计的锁相环可以实现转子位置的无静差跟踪。

3 系统的容错控制

容错控制是指控制系统在传感器，执行器发生故障时，闭环控制系统仍然能够保持稳定，并且系统仍满足一定的性能指标。文中针对速度传感器故障，采用一种基于数据融合的容错控制方案。

图6为文中所提出的容错控制方案原理框架。为了使速度传感器出现故障后，切换过程更加平稳，反馈转速ωrr采用数据融合的方法计算得到

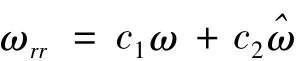
图6 容错控制原理Fig.6 Diagram of tolerant control

4 仿真实验结果及分析

为了验证文中所采用的容错控制方案在速度传感器故障下的性能，对所提出的系统进行了仿真研究。其中PMSM的参数为:定子电阻Rs=0.56Ω，直轴电感Ld=2.1 mH，交轴电感Lq=2.1 mH，转子磁通 ψf=0.175Wb，转动惯量 J=0.36 g·m2，电机极对数p=4，阻尼系数 B=94.4 μN·m·s，c1=0.75，c2=0.25。

首先，系统运行在带速度传感器模式下，负载大小为3 Nm，给定转速为1 500 r/min。0.3 s时速度传感器发生故障，故障后的系统响应如图7所示。

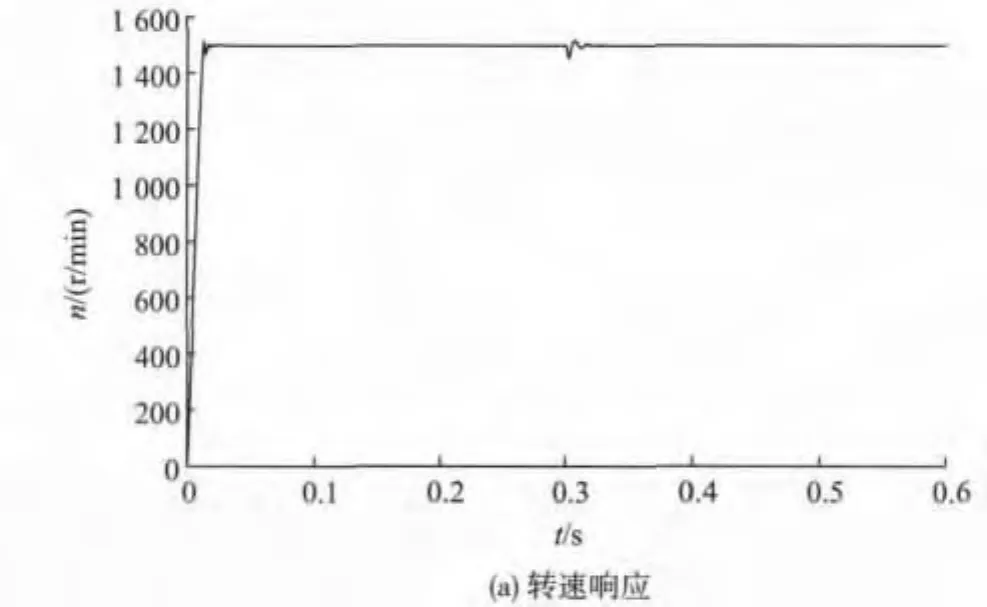
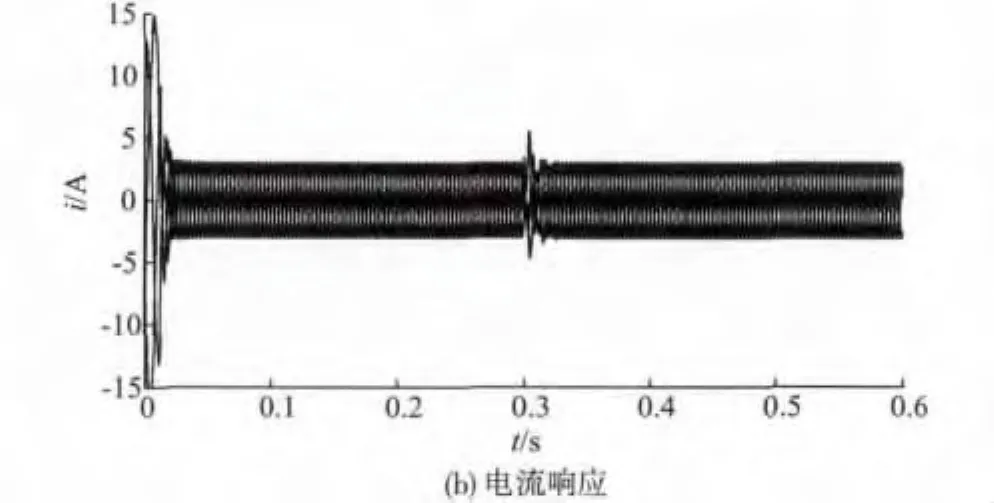
图7 速度传感器故障后系统响应Fig.7 System response after fault of speed sensor

由图7可以看出，系统可以在速度传感器出现故障后平滑地切换到无速度传感器控制模式下，而并不会发转速一直增大的现象。电机电流由于转速的波动而有所波动，但其很快进入稳定状态，并不影响系统后续的运行任务。

5 结语

文中针对永磁同步电机驱动系统中的速度传感器故障，提出一种基于数据融合技术的容错控制方案，使系统在速度传感器发生故障后，系统仍然可以稳定运行并且能够保证较好的性能指标。仿真结果表明，驱动系统能够在速度传感器故障的情况下稳定运行，提高了系统的可靠性，实现了在速度 传感器故障情况下的不间断运行。

［1］Tahami F，Shojaei A，Ahmadi Khatir D.A diversity based reconfig-urable method for fault tolerant control of induction motors［C］//International Symposium on Power Electronics，Electrical Drives，Automa-tion and Motion.Taormina，Italy:IEEE，2006:66-71.

［2］Bowes S，Sevinc A，Derrick Holliday.New natural observer applied to speed-sensorless DC servo and induction motors［J］.IEEE Transactions on Industrial Electronics，2004，51(5):1025-1032.

［3］Benaicha S，Nait-Said R，Zidani F，et al.Fuzzy fault tolerant control of an induction motor［J］.International Journal of Modeling，Identification and Control，2008，4(2):160-167.

［4］周桂法，王坚.基于神经网络的机车速度传感器故障诊断方法研究［J］.机车电传动，2010，1(1):36-38.ZHOU Guifa，WANG Jian.Research on locomotive speed sensor fault diagnosis method based on neural network［J］.Electric Drive for Locomotives，2010，1(1):36-38.(in Chinese)

［5］Espinoza-Trejo D R，Campos-Delgado D U.Active fault tolerant sc-heme for variable speed drives under actuator and sensor faults［C］//17th IEEE International Conference on Control Applications.San Antonio，Texas:IEEE，2008:474-479.

［6］富历新.一种光电码盘输出线断路检测和保护电路［J］.微电机，1993，26(3):56-57.FU Lixin.A kind of encoderwire disconnection detectionmethod and its protect circuit［J］.Micromotors Servo Technique，1993，26(3):56-57.(in Chinese)

［7］李世明.高故障容限变频器控制技术研究［D］.哈尔滨:哈尔滨工业大学，2010.

［8］刘家曦，李铁才，杨贵杰.永磁同步电机转子位置与速度预估［J］.电机与控制学报，2009，9(13):690-694.LIU Jiaxi，LITiecai，YANG Guijie.Rotor position and speed estimation for PMSM［J］.Electric Machines and Control，2009，9(13):690-694.(in Chinese)

［9］Burgos R P，Kshir sagar P，Lidozzi A，etal.Design and evaluationof a PLL-based position controller for sensorless vector control of permanentmagnet synchronousmachines［C］//32nd Annual Conference on IEEE Industrial Electronics，IECON 2006.Paris:IEEE，2006:5081-5086.