基于期权动态博弈理论的一层超额损失再保险定价模型构建

□白雯娟

中央财经大学保险学院



基于期权动态博弈理论的一层超额损失再保险定价模型构建

□白雯娟

中央财经大学保险学院

再保险是指在投保人和保险人所建立的原保险合同的基础上，通过双方签订再保险合同的方式，原保险公司将其所承担的风险转移给再保险公司的过程。原保险公司为再保险合同的分出人，再保险公司为再保险合同的分入人。所以，再保险也被称作“保险的保险”。美国保险信息协会的主席罗伯特·哈特维格甚至在金融危机后提出“保险公司是比银行更好的风险管理者”的观点，而再保险便是这个风险管理者最后的风险保障。分入的保费既要覆盖再保险人的成本，又要留出合理的利润空间，如何为这样一个重要的风险管理工具进行合理定价成为首要问题。

传统的保险定价都是基于合同双方是理性人的设定，但是我们在基础的定价原理中看不到决策者双方的决策顺序，这其实是不符合保险实务操作流程的。然而，博弈论的出现有效地解决了这个问题，博弈论是研究多人决策的理论工具，它考虑了理性行为人在给定的策略环境中如何采取行动以保证自己的效益最大化，并且是建立在考虑决策对手作出最优决策的前提下的。所以本文在原有的再保险定价原理的基础上，通过结合期权和博弈论的理论优势对再保险进行定价，制定出符合双方效用最大化的定价方案。

一、研究现状

(一)关于再保险定价模型的研究现状

传统的原保险定价有以下几种方式，包括净保费原理即平衡原理、期望值原理和方差原理等，当然保险定价还有多种原理，但基本是在以上理论的基础上衍生出来的。而再保险的定价没有非常统一的公式可以去遵循，典型的再保险定价公式为：再保险保费=(1+附加保费率)×再保险公司分担的理赔额期望值，等同于原保险的期望值原理。然而此种定价方式在粗略定价的同时，忽略了资金运作中的很多问题，比如再保险人在收取保费后并不是立即提供保险赔偿，而是在未来存在赔付的可能性，这期间再保险人可以通过资本市场的运作，达到资金保值增值的目的，此种情况下，上式的再保险保费明显被高估。同时，随着金融市场的快速发展，保险的外延不断扩大，尤其是衍生品市场的崛起，赋予了保险新的内涵。1995年，美国芝加哥期货交易所正式推出PCS期权(财产索赔服务期权，Property Claim Services Option)，开创了保险衍生产品的先河，自此，人们也越来越多地关注保险的期权性质。

(二)关于期权博弈理论的研究现状

关于期权博弈研究开创性的工作要归功于Smets，1993年,他最先将博弈模型和实物期权结合起来，建立了不确定条件下的对称双寡头期权博弈模型。1994年,Dixit和Pindyck对Smets 模型进行了总结，分析了不完全竞争情况下的案例。近些年，国外研究中也出现了将期权博弈理论运用在保险领域的实例，但基本是以定性研究为主。国内许多学者在国外研究的基础上，对期权博弈理论模型进行了深化研究。2001年，安瑛晖、张维针对传统企业项目投资估价和决策理论方法中存在的问题，总结归纳出期权博弈方法的一般化分析框架。2004年，石善冲、张维提出了期权博弈投资战略分析的思路、基本框架和具体分析步骤，并指出了期权博弈领域研究中存在的问题和研究方向。

该理论应用主要集中在战略和风险投资领域以及房地产领域。 2006年，孙建胜将金融框架下的期权博弈理论运用到保险领域，但也只是停留在定性研究的阶段。整体来看，期权博弈模型的运用主要是在实物期权方面，在保险领域中的运用还比较少，近些年出现了运用期权博弈模型来研究原保险定价问题的一些模型研究，而在再保险定价方面的研究还非常少。

二、期权动态博弈定价模型原理介绍

(一)期权特性在再保险中的运用

再保险同原保险的运作原理是一致的，都是由投保人向保险人支付保费，投保人通过保费的支付从而获得在保险事故发生时向保险人索赔的权利。在这种定义下，其实保险赋予了投保人一项或有索求权，这种权利可以看作是我们熟悉的期权，其中投保人支付的保费可以等同为期权费，如果保险事故在保险期限内发生，投保人就可以在合同到期前行使索赔权，并且在有免赔额的情况下，相当于期权中的美式期权提前行权的模式。再保险的原理与此一致，所以本文中，笔者便运用期权的定价技术来考虑再保险的定价问题。

本文重点分析一层超额损失再保险的定价模型，这类再保险在定价决策中只涉及一次分保过程，过程中也只包含一位原保险人和一位再保险人。设S为原保险合同的赔付额，D为再保险分出人的自留额，且我们的分析是在原保险人拥有足够大的同类保单的基础上。如果原保险赔付额S不大于再保险合同的免赔额D，则再保险人没有支付义务；如果S大于D，则再保险人需要承担S超过D的部分赔付额。所以，原保险人的保单到期价值可以描述为：

在本文的分析中，选用现代期权定价模型Black-Shcholes模型(以下简称“BS模型”)作为分析工具，它是在1973年由F. Black和M. Shcholes发展出的一种分析工具，能够有效地分析期权中或有权的定价，并且将资产的时间价值和风险投资纳入模型考虑，由于其所具有的优越性，BS模型被广泛用于金融产品的定价和资产的套期保值中。经过发展，现在经过修正的BS模型演变成一种一般性的分析框架，并更加广泛地运用于实物期权领域。BS经典模型如下所示：

Pt=StN(dt1)-Xe-rTN(dt2);

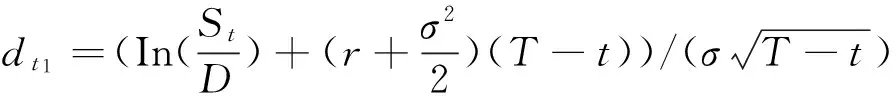
其中，St代表股票价格，在本文的研究中指原保险的赔付额，以S简化表示；X代表期权的执行价格，在本文中可以用一层超额损失再保险的免赔额D代替。

(二)完全信息动态博弈理论在再保险中的运用

传统的保险定价只是一种非策略性的理性人选择结果，合同中的参与方是在不知晓对方的情况下，完全根据自身最优化理论孤立地作出的决策。其实这种决策方式并不能够完全适用于保险的环境，尤其是再保险合同中，由于合同双方均是具有专业知识的保险机构，并且常见的再保险合同并不是格式化的，而是经过合同双方的反复博弈得出双方认同的费率、自留额和保额等。所以，本文在分析中运用博弈论的理论框架，极大地还原合同双方在签订合同时的决策考虑。

1.完全信息动态博弈理论框架在再保险中的运用

根据博弈双方在决策时是否能够相互影响从而订立一个有约束力的协议，博弈论分为“合作博弈”与“非合作博弈”。合作博弈更注重博弈双方的合作理性，非合作博弈则更强调决策个体的理性。其中，非合作博弈根据博弈方的决策顺序分为静态博弈和动态博弈，静态博弈指博弈双方同时进行决策，但并不知道对方的决策；而动态博弈则区分先后顺序，并且后序决策者能够充分地了解前序决策者的行为。另外，博弈论也可以按信息分布情况进行分类，如果博弈双方对彼此的决策信息完全知悉，则为完全信息博弈；如果不完全知悉，就为不完全信息博弈。结合以上两个维度，可以进一步将博弈论定义为四种形式，包括“完全信息静态博弈”“不完全信息静态博弈”“完全信息动态博弈”和“不完全信息动态博弈”。同时，这四种博弈形式对应四种均衡状态，分别是“纳什均衡”“贝叶斯纳什均衡”“子博弈精练纳什均衡”和“精练贝叶斯均衡”。本文将结合再保险合同中的期权特性，采用完全信息动态博弈理论来进行后续分析。

博弈论中的基本要素有：“局中人”，在再保险中相当于分出人和分入人；“行动”，是指原保险人的分出行为；“信息”，指分出人和分入人对对方的信息掌握情况；“策略”，指包括分出人的自留保费、分入人的费率厘定等的再保险计划；“支付”，即分出人与分入人个体的支付函数，由上节介绍的期权定价公式来代替。博弈当然遵循完全信息公开且博弈双方的决策有先后顺序，最终结果是博弈结束，即再保险合同合意时，博弈双方形成的能够使所有的局中人达到最优的均衡策略。

2.完全信息动态博弈理论的求解方法在再保险中的运用

在下图的示例中，两个局中人分别为Player(1)和Player(2)，他们对收益的结果有相同的判断，并且各自面对两种决策方式，前者是决策A和决策B，后者是决策C和决策D，收益组合(X,Y)表示Player(1)和Player(2)各自博弈收益，如结果(2P1,P2)表示，如果Player(1)选择决策A并且Player(2)选择决策C，那么Player(1)将得到2P1的收益，Player(2)将得到P2的收益，其中P1,P2表示任意一个正数。那么在这种情况下，Player(1)和Player(2)应该如何决策才能达到最优的状态。

这其实是描述了一个完全信息动态博弈的过程，在这个过程中有完全信息披露并且局中人有决策顺序，所以博弈求解相当于求解子博弈精练纳什均衡，可以采用常用的倒退归纳法来求解。先从博弈中的第二阶段开始，求解Player(2)的最优决策，比较C策略下的两种状态，第一个结果(2P1,P2)和第三个结果(-P1,-P2)中P2>-P2，所以当Player(2)选择C策略时的最优结果为(2P1,P2)。同样，当Player(2)选择D策略时的最优结果为(3P1,2P2)。

课后线上巩固学习 混合式教学的实施要注意线上教学和线下教学不是孤立的存在，教学过程应实现有机融合，并采取信息反馈的闭环教学模式，才能真正实现课堂翻转。如通过线下教学对某知识点的交流和讨论后，学生可重新回到线上观看相关微课，同时完成相关测试题，或在讨论区表达自己的学习体会和收获，都有助于进一步加深对该知识点的消化和理解。

那么，在Player(1)做决策时，他清楚地知道当选择策略A时，Player(2)当然会选择策略C；而选择策略B时，Player(2)当然会选择策略D。设定Player(1)的支付函数V1=( S1,S2,S)，Player(2)的支付函数V2=(S1,S2,S)， 其中S1表示Player

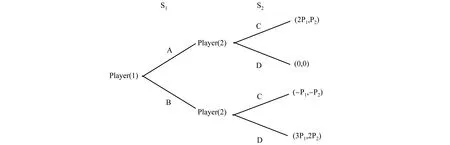
图 完全信息动态博弈过程示例

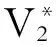
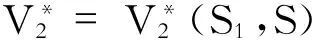
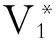
三、期权动态博弈定价模型基本框架构建

(一)期权动态博弈定价模型基本框架的要素定义

期权动态博弈定价模型，是把BS期权定价模型和动态博弈理论结合起来，由于BS模型的搭建是建立在无套利的前提下的，所以可以通过求解纳什均衡，得到一层超额损失再保险的理论价格。这个方式的实质是把局中人的支付函数用分出人和分入人的或有权用期权定价的技术加以确定，在双方先后决策的情形下，运用动态博弈的方法进行求解。这种方式的优点在于，当决策过程涉及再保险双方的动态决策分析时，合同双方的支付不固定，它是一个由诸多因素决定的内生变量，此时博弈论中设定的期望效用模型无法正确测量分保的风险，然而上节中介绍的BS期权定价模型则能够有效地为风险定价，所以二者的结合便能够有效分析再保险决策中双方的博弈过程。

在框架搭建之前，需要先对博弈中的基本概念进行了解，包括局中人、行动、信息、策略、收益、均衡和结果等。其中，局中人、策略和收益是最基本要素，局中人、行动和结果被统称为博弈规则。

那么根据上述博弈中的要素定义，再保险期权动态博弈过程中的要素可以描述为：第一阶段是再保险人决策过程，第二阶段是原保险人决策过程，再保险人在第一阶段制定出一个再保险合同的“免赔额”，其实是原保险人的自留额(D)，原保险人在观察到再保险人的D后，向再保险人购买一份自留额为D*的再保险合约，相当于购买了一份美式看涨期权，直到期权的价值最大化时选择执行期权。则再保险人通过签订再保合同的最终收益VR可以描述为下式：

EUR=EUVR=

+D)dF(S)}

原保险人的最终收益VI可以描述为下式：

VI=Max{-P,S-D*-P}

EUI=EUV1=EU(Max{-P,S-D*-P})

其中，D*表示原保险人认为能够达到最大期权价值即期权执行时的再保险自留额。

原保险公司的效用函数设定方面，由于保险公司具有有效的风险分散机制，因此U(X)=a+bX。并且保险公司就是给风险定价的单位，它拥有数量巨大的风险单位，所以在一般的分析中设定保险公司对风险的态度为“风险中性”。

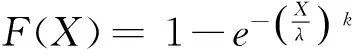
(二)期权动态博弈定价模型基本框架的构建

通过上述分析，我们知道，在再保险合同的签订过程中，合同双方原保险人和再保险人如何制定最优决策是相互影响的，因此可以用两个阶段的动态博弈来描述这一决策过程：第一阶段，再保险人制定自留额D；第二阶段，原保险人进行是否行权的决策。决策问题中支付函数用BS期权定价模型确定，因此可得到符合实际的一层超赔损失再保险的正确定价。可用以下三个步骤来进行描述：

首先，定义博弈双方即局中人的博弈要素，包括行动顺序和支付函数；

其次，运用BS期权定价模型确定局中人的未来不确定支付；

最后，运用倒推归纳法从第二阶段开始求解均衡结果。

通过这样的分析框架的搭建，对原本复杂的动态分析过程进行简化求解，既拥有了期权定价包含货币的时间价值和风险的价格优势，又结合了动态博弈理论的策略化的分析过程，更准确地还原了再保险合同签订时合同双方的决策考虑，并且将这种复杂动态金融条件下的决策转化为只需要寻找再保险人的期望效用对原保险人自留额一阶导数等于零的简单计算。

四、期权动态博弈框架下一层超赔损失再保险无套利求解

前文已经讲述过求解完全信息下的动态博弈的方法即倒推归纳法，首先确定第二阶段中原保险人在观察到自留额D后的效用最大化策略。我们知道，一般情况下，再保险合同只有在签订和到期时才有现金流动，这相当于合同双方签订了不分红的美式看涨期权。那么在原保险人的立场上，提前行权没有意义，因为美式看涨期权和欧式看涨期权在无分红时的期权最小价值相等，均可以表示为

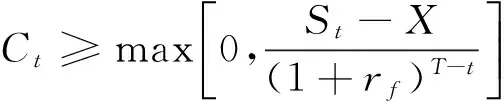
再保险人的效用最大化问题表示为：

Max(EUR)=

+D-S)dF(S)}

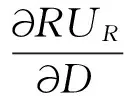
上述公式表明了S和D之间的关系，给定任意的S值可以得到基于动态博弈理论的最优再保险自留额和分出额。其中，k=2.0207，λ=2691.5(求解过程略)；设定b=1(保险公司的风险态度为中性)，那么可以得到一个只包含S和D的等式，设定不同的S，就可以得到相应的D。

通过对上式的计算得到的D等于D*。这个D*就是Player(1)即再保险人在分析Player(2)原保险人能够达到最优P0的基础上的最优自留额，博弈过程即再保险人在博弈的第一阶段确定D*，然后在第二阶段，原保险人在此基础上选择令自己效用最大化的时机行权，这样，双方都在合同中得到了相对最大化的效用。那么最终得到的博弈均衡解为(D*,P0(D*))，其中的P0(D*)是我们基于无套利定价原理分析得到的一层超额损失再保险的公平定价。

五、关于期权动态博弈定价模型的一些结论

(一)期权动态博弈定价模型求解过程中的函数设定问题

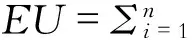
原保险赔付额X的分布函数F(X)的设定在本文中是采用韦伯分布来定义的。虽然韦伯分布广泛运用于自然灾害的损失定价，但是关于损失分布函数的确定还没有一个非常普适的结论，包括最常见的损失均匀分布的设定也只能在诸多约束条件下才能够成立。并且，由于损失分布在不同的合同责任项下有着很大的区别，仅仅财产险部分就有几十种风险属性所对应的风险分布。再加上地区、环境等诸多影响因素的存在，令损失分布函数并不十分容易确定。所以，在后续的研究中可以尝试其他损失分布的情况。

(二)期权动态博弈模型的推广运用

本文运用期权动态博弈模型来分析一层超额损失再保险的定价问题，我们可以基于模型中的基本理论将模型推广到多层的超赔再保险定价问题中，其实质就是将两阶段的博弈过程扩展到三阶段、四阶段等，相应的“局中人”也随之不断增加。我们还可以将模型求解过程中得到的D*加以运用，用以分析最优分出额问题，因为原保险人的自留额决策关系到双方的经营效益，是个非常重要的效益中间指标。同时，该模型不仅可以分析再保险的情形，还可以适用于原保险合同中分析投保人和保险人的最优决策。