剪切流场下液滴碰撞的流变特性

王程遥 张程宾 陈永平,3 张 林

(1东南大学能源与环境学院,南京 210096)(2中国工程物理研究院激光聚变研究中心,绵阳 621900)(3扬州大学水利与能源动力工程学院,扬州 225127)

剪切流场下液滴碰撞的流变特性

王程遥1张程宾1陈永平1,3张 林2

(1东南大学能源与环境学院,南京 210096)(2中国工程物理研究院激光聚变研究中心,绵阳 621900)(3扬州大学水利与能源动力工程学院,扬州 225127)

基于VOF液/液相界面追踪方法,建立了不可压缩水/油单乳液液滴动力学模型并进行数值求解,模拟研究了剪切流场条件下2个相同体积的液滴在碰撞过程中的相互作用及变形行为．观察了液滴碰撞过程中液滴的运动轨迹,并对相应的内在机理进行了分析．在剪切流场作用下,两液滴的碰撞过程分为接近、碰撞、分离3个阶段．由于碰撞过程中液滴间的相互挤推作用,液滴分离后,液滴间的侧向质心间距Δy/a增大．此外,分析了液滴碰撞过程中毛细数对液滴间相互作用的影响．两液滴在碰撞靠近过程中,在碰撞区中心处产生一个高压区,随着毛细数Ca从0.2增加到0.4,界面挤压变形越明显,液滴变形系数D也从0.32增加到0.51．

液滴;碰撞;剪切流场;VOF方法

液滴动力学是多相流学科和乳液工程技术的重要研究领域,液滴碰撞过程的流变行为是乳化、共混等工业过程[1-3]中主动调控的重要理论基础．因此,准确掌握碰撞过程中液滴的流变行为、内在机理及其影响规律不仅对液滴动力学理论研究方向具有重要的学术价值,而且对于有效地控制液滴工艺流程具有重要的现实意义．

目前,国际上已对单个液滴的流变行为开展了较为深入的研究．20世纪30年代,Taylor等[4-5]就对单个液滴在流场中变形与破裂行为开展了实验研究．随后,Rallison等[6]、Youngren等[7]对单一液滴的形变行为进行了数学建模和数值模拟．Stone[8]则对单液滴在流场中流变行为的实验与理论工作进行了总结,综述了液滴界面动力学方面的研究进展,着重介绍了流体物性参数和不同的流场类型等因素对液滴形变和液滴破碎的影响．最近,Salkin等[9]对液滴在流场中遇到障碍物的破碎行为进行了实验研究．Ulloa等[10]实验研究了剪切流场的受限程度对液滴形变与破碎的影响．刘向东等[11]采用VOF方法对剪切流场中的单个双乳液液滴进行了液滴形变及破碎特性的研究,结果表明液滴的稳定形变随着毛细数的增大而加剧,并且在给定的雷诺数下存在一个临界毛细数,小于临界毛细数时,液滴只发生稳定变形,反之液滴破碎．

相比于单个液滴在外流场中的流变行为,2个或者更多液滴在外流场的碰撞过程中存在液滴间的相互作用,使得其流变机理变得更加复杂．目前,已有少部分学者在此领域开展了相关的实验研究,针对液滴在剪切流场中碰撞过程的运动轨迹进行了可视化观测[12-13],但受到量测手段的限制,对液滴在剪切流场中相互碰撞过程的形变与碰撞的耦合机理以及压力变化特性尚未充分揭示．为此,本文基于VOF(volume of fluid)液/液相界面追踪方法,建立了不可压缩水/油单乳液液滴动力学模型并进行数值求解,模拟研究了在剪切流场作用下2个相同体积的球形液滴在碰撞过程中的变形、相互作用及压力演化．

1 数学模型

双板平行剪切流场下2个半径a=100 μm的油滴在基质水中的初始位置如图1所示,流动方向为x方向,速度梯度方向为y方向,2个液滴关于中心点对称,x方向与y方向的初始质心距分别为Δx和Δy．2块平板在2个平行平面上分别以相同速度U=0.02 m/s向相反的方向滑动,产生剪切率G=2U/H的恒定剪切流场(H为两板间距),作用于液滴从而产生运动变形．剪切流场的左右两侧边界采用周期性边界条件．

在剪切流场下,液滴的碰撞现象实质上是一种液/液相界面的运动与变形所产生的宏观结果．本文采用保持质量守恒性较好的VOF方法[14]来描述相界面的位置及其运动．VOF方法就是通过研究网格中每一相的体积比函数αi来确定介质面、

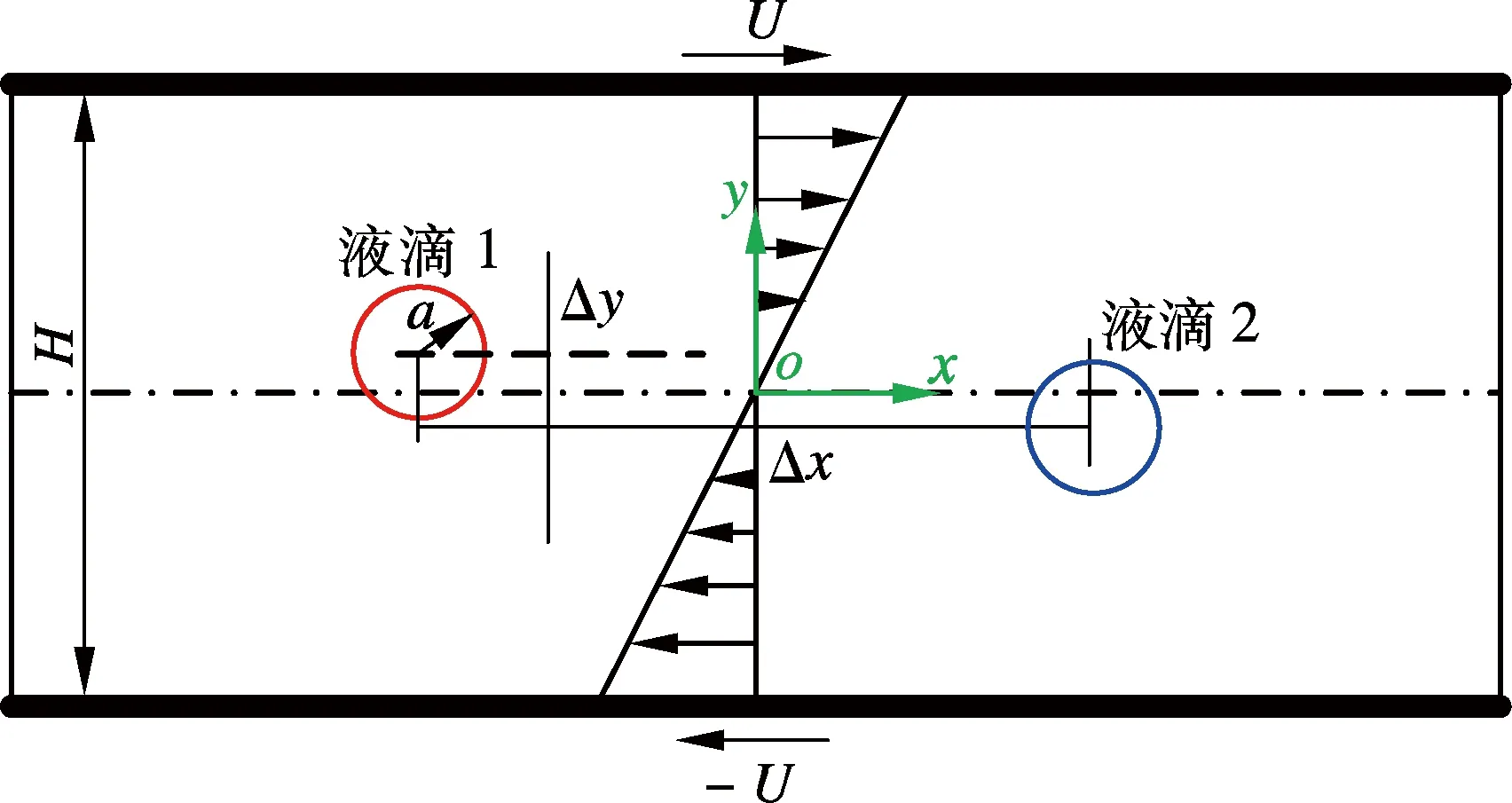
图1 双板平行剪切流场下两个液滴初始位置示意图

自由面、间断面以及其他内部运动界面,能够捕获各种不规则形状的自由表面,可以较好地模拟乳液液滴在流场中的变形、碰撞等复杂的变化．定义连续相m、离散相d两相的体积比函数分别为αm和αd,则αm+αd=1．

在整个流场计算区域内，满足以下输运方程：

(1)

整个流场区域满足以下连续性方程：

(2)

动量方程

(3)

其中

ρ=∑αiρi

(4)

μ=∑αiμi

(5)

式中,v为流体速度;ρ和μ分别为流体的密度和动力黏度；张力源项Fvol采用CSF(continuum surface force)方法[15]计算,即

(6)

式中,m相和d相之间的界面曲率为

(7)

在简单剪切流中,液滴碰撞变形主要受到惯性力、黏性力及相界面张力的作用．为表征各相参数及各种作用力间的相对大小,本文引入以下参数:Reynolds数(Re=ρmGa2/μm)表征惯性力与黏性力之间的相对大小;Capillary数(Ca=μmGa/σ)表征黏性力和表面张力之间的相对大小,其中，界面张力系数σ=10-5N/m;黏度比λ=μd/μm;密度比β=ρd/ρm.μd=μm=0.001 Pa·s,ρd=ρm=1 000 kg/m3．为表征液滴碰撞过程中的变形程度,引入Taylor变形系数[1-2]D=(L-B)/(L+B),其中L和B分别为发生变形后的椭圆形液滴的长轴与短轴．本文将初始液滴半径a作为特征长度,剪切率的倒数G-1作为特征时间，则无量纲时间t*=t/G,液滴的初始位置参数为(Δx0/a, Δy0/a)．

对图1两平行平板之间的流场进行矩形网格划分．流体流动控制方程(即方程(1)～(3))采用有限体积差分法进行数值求解．在求解过程中,压力场和速度场的耦合采用SIMPLE算法,动量方程采用一阶迎风差分格式离散,基于分段式界面计算(PLIC)方法的Geo-Reconstruct格式对液/液界面进行重构．控制微分方程经离散成为线性代数方程组后,采用Gauss-Seidel方法进行迭代求解．迭代计算中所采用的欠松弛因子分别为:压力项0.2,密度项0.5,体积力源项0.5,动量源项0.2．采用不同的网格尺寸进行网格独立性检测,以确保所得的数值解均为网格独立的解．时间步长取0.1 ms,当每个迭代时间步的流体速度残差小于10-3时,认为该时间步迭代计算收敛．

本文对Guido等[12]开展的液滴碰撞实验进行了数值模拟对比,如图2所示.由图可见，液滴碰撞演化过程的数值模拟结果与实验结果吻合较好,表明本文所建立的模型准确可靠．

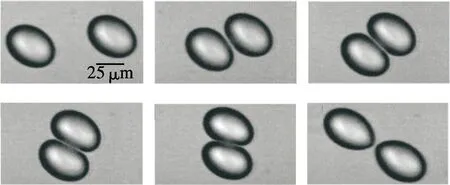
(a) 液滴碰撞的实验图片

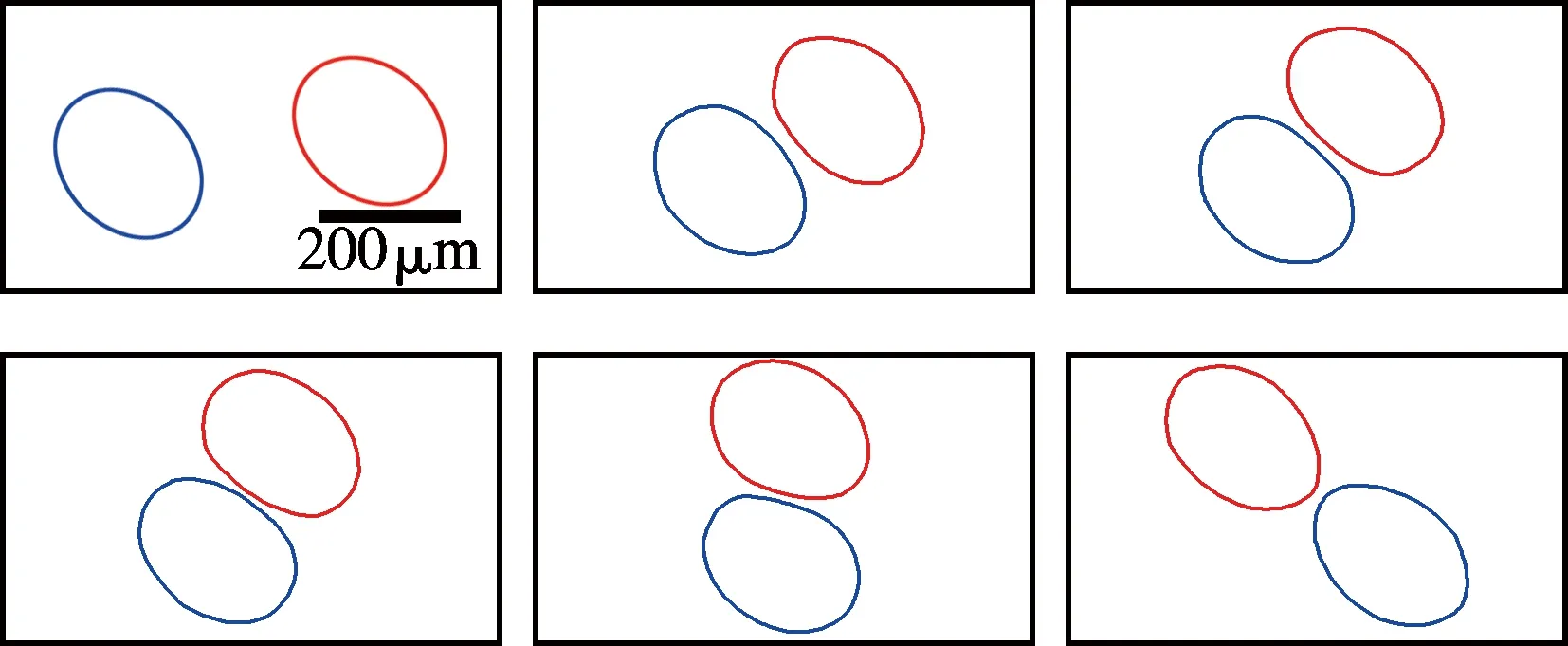
(b) 数值模拟的结果

2 结果分析与讨论

2.1 碰撞过程中液滴间的相互作用

为研究剪切流场下2个液滴碰撞过程的流变特性,本文对Re=0.2,Ca=0.2，H=2 mm条件下2个相同大小的液滴在剪切流场中的碰撞过程进行数值模拟．液滴在x方向与y方向的初始质心距分别为Δx0/a=4, Δy0/a=0.8．图3给出了液滴在剪切流场中经历碰撞过程的运动轨迹．由于液滴间的相互作用,液滴间的y向距离先增大后减小,随后稳定于一个值,最终的y向距离比初始的距离大．由图可知,随着剪切流场开始作用,液滴先变形为椭圆状,随后在流场拖曳力的作用下,液滴相互靠近并碰撞,直至液滴最终相互绕过对方,完成碰撞．在碰撞过程中,受液滴间强烈的相互作用影响,液滴产生了剧烈形变,以致在2个液滴碰撞作用处分别形成了一个平滑界面．随后,两液滴以流场中心为对称轴旋转并相互绕过对方后分离,当液滴完全分开后,液滴形状恢复为碰撞前的椭圆状．

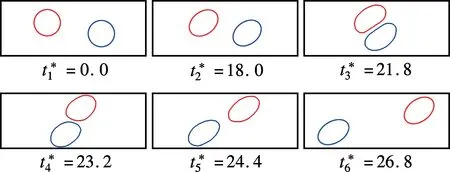
(a) 液滴碰撞过程时间序列图

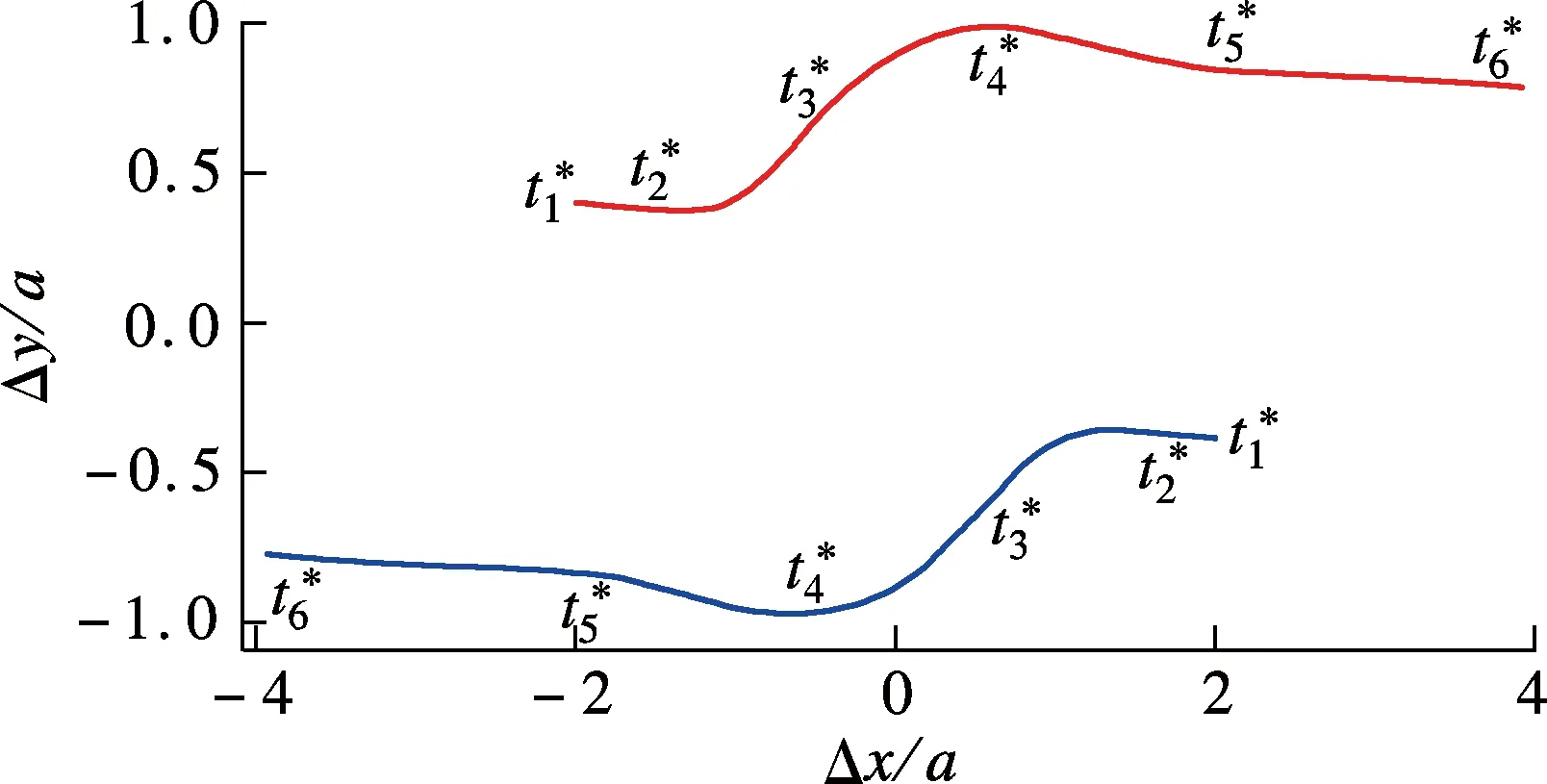
(b) 两液滴相对位置轨迹

为了更好地理解液滴碰撞过程中的流变行为,图4给出了与图3相对应时间点的碰撞过程压力分布时间序列图,图中的压力是以101 325 Pa为基准的相对压力值．如图所示,随着施加外剪切流场,液滴开始变形,在表面张力的作用下,在变形液滴长轴方向的端部区域出现高压区,从而在长轴端部的界面内外形成较高的压力梯度．根据Young-Laplace方程Δp=2σ/R,界面两端的压力梯度与界面曲率半径R呈反比关系,因此,在长轴端部高压力梯度区所对应的液滴相界面的界面曲率半径较小(见图4(b))．随后液滴相互靠近,液滴之间液膜的压力开始变大,促使液膜排液,液膜厚度逐渐减小,当液膜最薄时,液膜间的压力达到最高值(见图4(c))．此时,膜压的增大使得液膜产生挤压作用,使液滴碰撞面附近产生大的变形,液滴的相对接触面变平甚至凹陷．当液滴开始分开,液滴间的液膜厚度增加,同时伴随着液滴的回缩,流场中心的压力快速下降,变为负压(见图4(d)～(e))．在压力下降至极低值时,低压区产生抽吸效应,在y方向上产生了一个拖曳力,减小了该阶段中液滴y向的质心距(见图4(e))．同时,液滴的形状出现短暂不对称的现象,液滴相对的端部出现高曲率的尖端．在Guido等[12]的实验中也观察到了类似的抽吸现象．最终,液滴完全分开,如图4(f)所示．

图4 液滴碰撞过程压力分布图

图5给出了碰撞过程中液滴变形系数的变化趋势．随着液滴相互靠近,变形量开始变大;当液滴相互对齐挤压时,液滴的形变量最大;随之液滴相互越过对方,当液滴开始分开时,出现负压抽吸效应,液滴被短暂拉长,形变量达到第2个最大值;当液滴完全分开后,液滴形状恢复,随后基本保持不变．

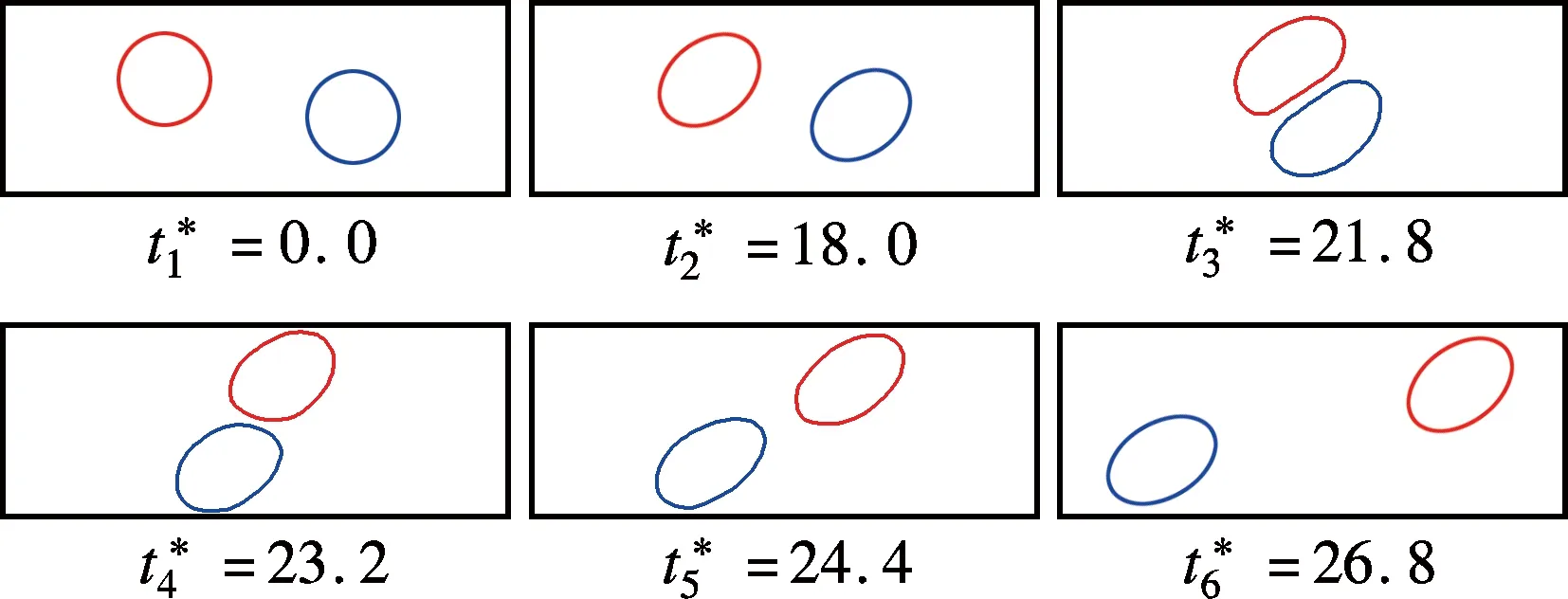
(a) 液滴碰撞过程时间序列图

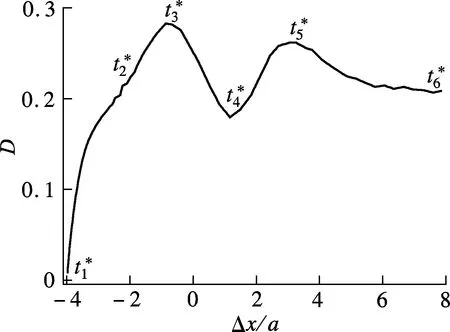
(b) 液滴形变趋势

2.2 Ca数的影响

为研究不同的Ca数对液滴碰撞的影响,本文在H=1.0mm，Ca=0.2,0.3,0.4的条件下对液滴碰撞过程进行数值模拟研究,结果如图6所示．由图可知,Ca数的影响主要体现在液滴的形变上,Ca数表征了促使液滴变形的黏性剪切力与抵抗液滴变形的表面张力的比值.Ca数越大,黏性剪切力的相对值就增大,从而导致液滴的变形程度增大．同时,随着Ca数的增大,剪切力增大,碰撞过程中,剪切流场对2个液滴的外围挤推作用增强,强化了对碰撞面的挤压作用,因此,两液滴碰撞面处的界面内凹现象变得愈加明显．

图6 不同Ca数下液滴的形变

3 结论

1) 在剪切流场作用下,两液滴碰撞过程分为接近、碰撞、分离3个阶段．碰撞过程中,液滴先变形为椭圆状,随后相互靠近、碰撞,然后液滴相互绕过对方,最终,两液滴分离并恢复至碰撞前的椭圆状．由于碰撞过程中液滴间的相互挤推作用,液滴分离后,垂直于液滴碰撞方向的质心间距增大．

2) 碰撞过程中,随着液滴相互靠近,液滴的变形量开始变大;当液滴碰撞并相互挤压时,液滴的形变量最大;随之液滴相互绕过对方并分开,此时,由于低压区的抽吸拖曳效应,两液滴相对的端部出现尖端,液滴形变量达到第2个最大值;当液滴完全分开后,液滴形状恢复．

3) 碰撞过程中,液滴碰撞区域处会形成平滑界面．两液滴碰撞靠近过程中,在碰撞区中心处产生一个高压区,使得两液滴间的液膜对碰撞的界面产生挤压作用,碰撞界面变平,并且随着毛细数Ca从0.2增加到0.4,界面挤压变形越明显,液滴变形系数也从0.32增加到0.51．

References)

[1]Jafari S M, Assadpoor E, He Y H, et al. Re-coalescence of emulsion droplets during high-energy emulsification [J].FoodHydrocolloids, 2008, 22(7): 1191-1202.

[2]Lobo L, Svereika A. Coalescence during emulsification: 2. role of small molecule surfactants [J].JournalofColloidandInterfaceScience, 2003, 261(2): 498-507.

[3]Ramic A J, Hudson S D, Jamieson A M, et al. Temporary droplet-size hysteresis in immiscible polymer blends [J].Polymer, 2000, 41(16): 6263-6270.

[4]Taylor G I. The viscosity of a fluid containing small drops of another fluid [J].ProceedingsoftheRoyalSocietyA:MathematicalPhysicalandEngineeringSciences, 1932, 138(834): 41-48.

[5]Taylor G I. The formation of emulsions in definable fields of flow [J].ProceedingsoftheRoyalSocietyA:MathematicalPhysicalandEngineeringSciences, 1934, 146(858):501-523.

[6]Rallison J M, Acrivos A. A numerical study of deformation and burst of a viscous drop in an extensional flow [J].JournalofFluidMechanics, 1978, 89(1):191-200.

[7]Youngren G K, Acrivos A. On the shape of a gas bubble in a viscous extensional flow [J].JournalofFluidMechanics, 1976, 76(3):433-442.

[8]Stone H A. Dynamics of drop deformation and breakup in viscous fluids [J].AnnualReviewofFluidMechanics, 1994, 26: 65-102.

[9]Salkin L, Courbin L, Panizza P. Microfluidic breakups of confined droplets against a linear obstacle: the importance of the viscosity contrast [J].PhysicalReviewE, 2012, 86: 036317-1-036317-6.

[10]Ulloa C, Ahumada A, Cordero M L. Effect of confinement on the deformation of microfluidic drops [J].PhysicalReviewE, 2014, 89: 033004-1-033004-6.

[11]刘向东, 陈永平, 张程宾, 等. 双乳液液滴形变及破碎特性[J]. 工程热物理学报, 2012, 33(3): 457-459. Liu Xiangdong, Chen Yongping, Zhang Chengbin, et al. Deformation and breakup characteristics of double emulsion drop [J].JournalofEngineeringThermophysics, 2012, 33(3): 457-459.(in Chinese)

[12]Guido S, Simeone M. Binary collision of drops in simple shear flow by computer-assisted video optical microscopy [J].JournalofFluidMechanics, 1998, 357:1-20.

[13]Tretheway D C, Muraoka M, Leal L G. Experimental trajectories of two drops in planar extensional flow [J].PhysicsofFluids, 1999, 11(5): 971-981.

[14]Hirt C W, Nichols B D. Volume of fluid (VOF) method for the dynamics of free boundaries [J].JournalofComputationalPhysics, 1981, 39(1): 201-225.

[15]Brackbill J U, Kothe D B, Zemach C. A continuum method for modeling surface tension [J].JournalofComputationalPhysics, 1992, 100(2): 335-354.

Rheological behavior of interactive drops in shear flow

Wang Chengyao1Zhang Chengbin1Chen Yongping1,3Zhang Lin2

(1School of Energy and Environment, Southeast University, Nanjing 210096, China)(2Research Center of Laser Fusion, China Academy of Engineering Physics, Mianyang 621900, China)(3School of Hydraulic, Energy and Power Engineering, Yangzhou University, Yangzhou 225127, China)

Based on VOF (volume of fluid) liquid-liquid interface tracking method, a model for incompressible water-oil emulsion drop hydrodynamics is developed and numerically solved to study the hydrodynamic interaction and deformation behavior between two equal-sized drops during the collision in a shear flow. The motion trajectory during the collision is observed and the corresponding underlying hydrodynamics are analyzed. Under the shear flow, drop behavior during the collision can be divided into three stages: approach, collision and separation. Due to the hydrodynamic interaction between the drops, the final lateral separation of drop mass centers Δy/aincreases after the drop separation. In addition, the effects of the capillary number on the hydrodynamic interaction between two interactive drops are also analyzed. During the collision, a high pressure region is observed at the center of the flow domain. As the capillary number increases from 0.2 to 0.4, the interface deformation is more obvious and the deformation coefficientDof the drop increases from 0.32 to 0.51.

drop; collision; shear flow; volume of fluid method

10.3969/j.issn.1001-0505.2015.02.020

2014-12-07. 作者简介: 王程遥(1988—),女,博士生;陈永平(联系人),男,博士,教授,博士生导师, ypchen@seu.edu.cn.

江苏省自然科学基金资助项目(BK20130009,BK20130621)、中国工程物理研究院科学技术发展基金资助项目(2012A0302015).

王程遥,张程宾,陈永平,等.剪切流场下液滴碰撞的流变特性[J].东南大学学报:自然科学版,2015,45(2):309-313.

10.3969/j.issn.1001-0505.2015.02.020

TK124

A

1001-0505(2015)02-0309-05