一个双参数的共轭梯度法簇

马文亚

考虑无约束优化问题

其中f:Rn→R是一个连续可微的函数.

共轭梯度法是求解问题(1)的具有迭代格式

的一类方法,其中αk是某种线搜索下的步长,dk满足

其中βk是共轭参数.βk的不同取法对应于不同的非线性共轭梯度法.著名的PRP[1,2]、HS[3]、LS[4]方法的参数βk分别为

其中,‖·‖为欧几里得范数,yk-1=gk-gk-1.

最近,文献[5]和[6]提出如下βk公式

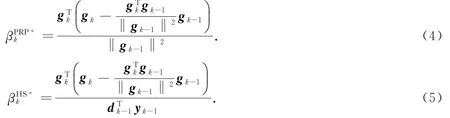
在共轭梯度法的许多理论分析和数值实现中,常常使用强Wolfe线搜索.其要求αk满足

和

其中0＜δ≤σ＜1.

共轭梯度法收敛性分析中常用的充分下降性条件为

受文献[5,6]启发,本文提出带双参数的新的βk公式

其中参数μ,μ2,μ1+μ2∈ [0,1].

1 算法

初始步 给定初始点x0∈Rn,μ1,μ2∈[0,1](且满足μ1+μ2∈[0,1])δ∈(0,1),σ∈(0,1),ε＞0.令d0=-g0,k=0.

步骤1 若‖g0‖≤ε,则停止;

步骤2 由强Wolfe线搜索准则计算步长αk;

步骤3 令xk+1=xk+αkdk,若‖gk+1‖≤ε,则停止;

步骤4 由式(9)计算βk+1,由式(3)计算dk+1;

步骤5 令k=k+1,转步骤2.

2 算法的收敛性

为了证明新算法的全局收敛性,首先给出两个假设:

(A)水平集Ω={x∈Rnf( x)≤f( x0)}有下界,其中x0∈Rn为初始点.

(B)f在水平集Ω的一个领域Ν内连续可微,且其梯度g满足Lipschitz连续,即存在常数L＞0,使得

引理1[7]假设(A)-(B)成立,设序列 gk{}和 dk{}由上述算法产生,并设步长αk由强Wolfe线搜索计算.则

引理2 考虑上述算法生成的序列 gk{}和 dk{},则存在常数c＞0,使得∀k≥1,式(8)成立;∀k≥2,有βk≥0.

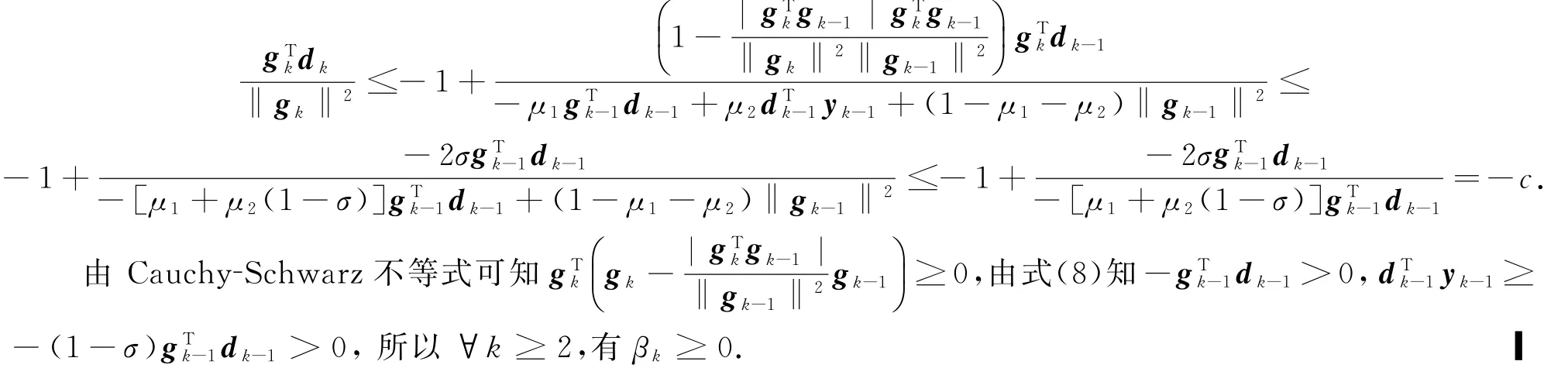
性质 (*)[8]考虑由式(2)-(3)构成的迭代方法,假设

如果存在常数b＞1和λ＞0,使得对所有的k有|βk|≤b,以及成立,则称该迭代方法具有性质(*).

引理3 假设(A)-(B)成立,考虑上述算法生成的序列 βk{},假定式(12)成立,则 βk{}满足性质(*).

证 设q=cμ1+cμ2(1-σ)+(1-μ1-μ2),则0＜q＜1.取.由式(6),(7),(9),(12),Cauchy-Schwartz不等式和引理1可得

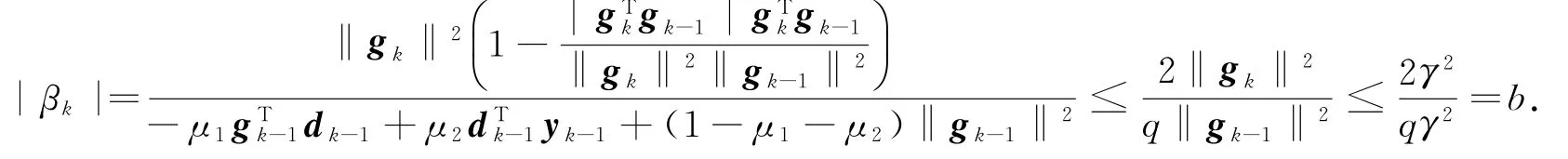
设 ‖sk-1‖ ≤λ,则

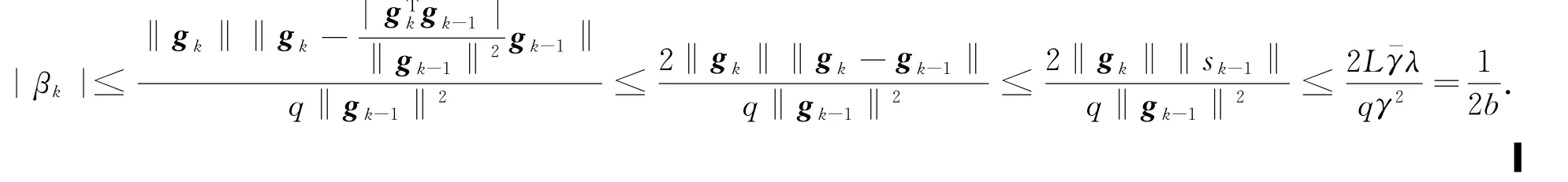
定理 假设(A)-(B)成立,设序列 g k{}和 dk{}由上述算法产生,则

证 由引理1、引理2、引理3知,结论成立.❙

参考文献:

[1]Polyak B T.The conjugate gradient method in extreme problems[J].USSR Computational Mathematics and Mathematical Physics,1969,9(4):94-112.

[2]Polak E,Ribiere G.Note sur la convergence de directions conjugues[J].Rev Francaise Informat Recherche Operatinelle,1969,16:35-43.

[3]Hestenes M R,Stiefel E L.Methods of conjugate gradients for solving linear systems[M].Washington,DC:National Bureau of Standards,1952:409-436.

[4]Liu Y L,Storey C S.Efficient generalized conjugate gradient algorithms,Part 1:Theory[J].Journal of Optimization Theory and Applications,1991,69(1):129-137.

[5]Huang H D,Li Y J,Wei Z X.Global Convergence of a Modified PRP Conjugate Gradient Method[J].Journal of Mathematical Research and Exposition,2010,30(1):141-148.

[6]Wei Z X,Huang H D,Tao Y R.A Modified Hestenes-Stiefel Conjugate Gradient Method and Its Convergence[J].Journal of Mathematical Research and Exposition,2010,30(2):297-308.

[7]Zoutendijk G.Nonlinear programming,computational methods[J].Integer and Nonlinear Programming,1970,143(1):37-86.

[8]Gilbert J C,Nocedal J.Global convergence properties of conjugate gradient methods for Optimization[J].SIAM Journal on Optimization,1992,2(1):21-42.