一种修正的LS共轭梯度法

焦佳佳

考虑无约束优化问题

其中R n是n维欧几里得空间,f:Rn→R是一个连续可微的函数.

众所周知,共轭梯度法是求解该类问题的一种重要方法,它具有如下的迭代格式

其中αk是某种线搜索下的步长,dk满足

其中βk是共轭参数.不同的βk的取法会产生不同的共轭梯度法,常见的βk有如下定义:

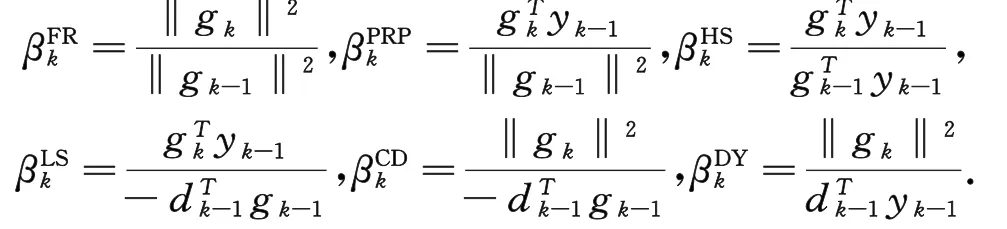
对应的方法分别叫做FR(Fletcher-Revees),PRP(Polak-Ribiere-Polyak),HS(Hestenes-Stiefel),LS(Liu-Storey),CD(Conjugate Descent)和DY(Dai-Yuan)共轭梯度法.常用的线搜索有:Wolfe线搜索,强Wolfe线搜索,Armijo-type线搜索等,其中强Wolfe线搜索要求αk满足

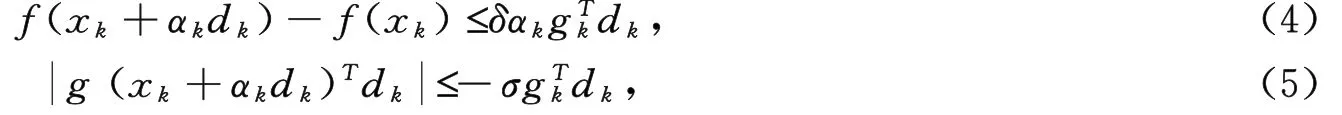
与其他共轭梯度法相比,PRP方法的数值表现是目前认为最好的方法之一,但该方法的收敛性不理想.研究发现,PRP方法收敛性不好的原因在于它不具有充分下降性.充分下降性是指,对所有的k,不等式

成立,其中c为常数.此性质在收敛性分析中起着非常重要的作用.因此,许多学者都希望找到数值表现可与PRP相媲美同时性质又比其好的方法.文献[1]将标准的共轭梯度法迭代格式(3)推广为如下谱共轭梯度形式

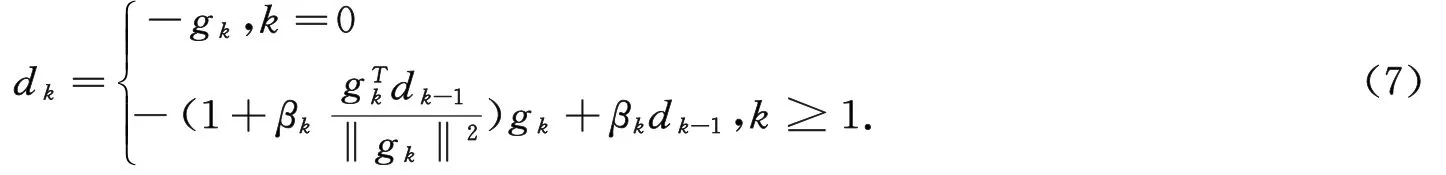
文献[2]取βk=βkFR,在式(7)下满足gkTdk=-‖gk‖2.本文受这些思想的启发,基于谱共轭梯度法迭代式(7),考虑如下参数

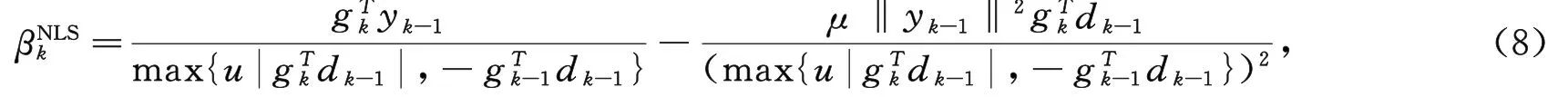
结合强Wolfe线搜索建立新的谱共轭梯度算法,并分析了算法的全局收敛.

NLS算法:

初始步:给定x0∈Rn,ε≥0.令d0=-g0,k=0.

第一步:若 ‖g0‖ ≤ε,则停止;

第二步:求出满足强Wolfe线搜索的步长αk;

第三步:计算xk+1=xk+αkdk,若 ‖gk+1‖ ≤ε,则停止;

第四步:通过式(5),(6),求得dk+1;令k=k+1,转第二步.

为了讨论新算法的全局收敛性,假定目标函数满足如下基本假设:

(A)水平集Ω={x∈Rnf( x)≤f( x0)}有下界,即存在常数a＞0,使得 x≤a.

(B)f在水平集Ω的一个邻域Ν内连续可微,且其梯度g满足Lipschitz连续,即存在正的常数L,使得

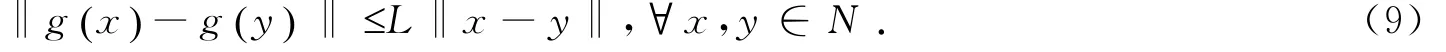
显然,在上述假设下,存在某个正的常数Γ,使得

引理1 若假设(A)和(B)成立,考虑方法(2)和(3),其中dk满足强Wolfe线搜索(4)和(5),则有

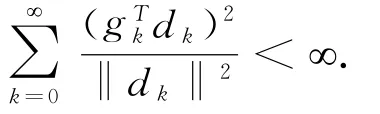
引理2 在假设(A)和(B)成立的条件下,序列 xk{}由算法NLS产生,αk满足强Wolfe线搜索(4)和(5).如果存在一个常数ε＞0使得对所有的k＞0有‖gk‖≥ε,则存在正的常数C和M使得

和

成立.

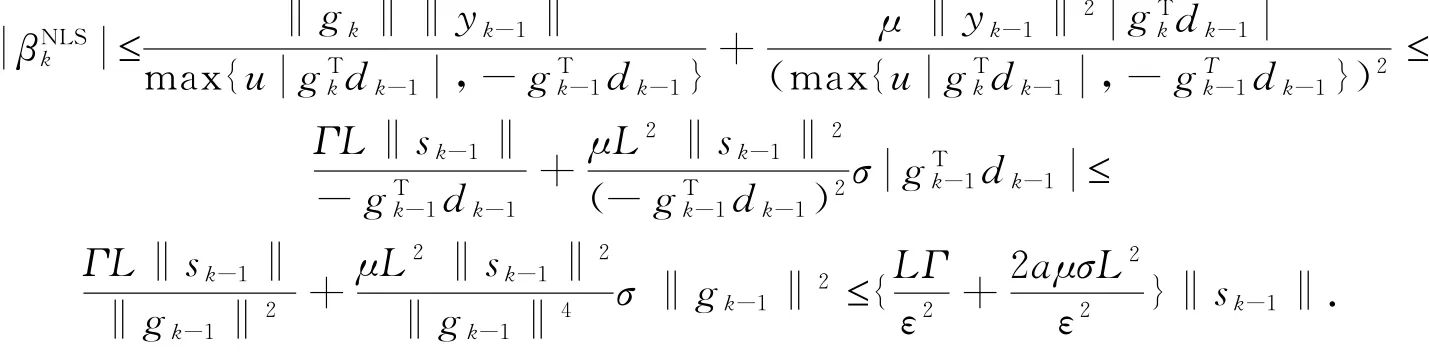
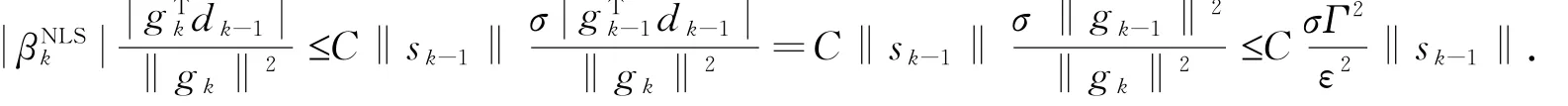
引理3 若假设(A)和(B)成立,序列 xk{}由算法NLS产生,αk满足强Wolfe线搜索(4)和(5).如果存在一个常数ε＞0使得对所有的k＞0有‖gk‖≥ε,则有

该引理的证明类似于文献[3]中引理3.2的证明,所以在此处省略该引理的证明.

定理1 若假设(A)和(B)成立,序列 xk{}由算法NLS产生,αk满足强Wolfe线搜索(4)和(5),则有

该定理的证明类似于文献[3]中定理3.1的证明,所以在此处省略该算法的全局收敛性证明.

对于求解大规模的无约束优化问题,给出了一种修正的谱LS共轭梯度法,该方法不依赖任何线搜索具有充分下降性,并且在强Wolfe线搜索下证明了该方法的全局收敛性.

参考文献:

[1]Birgin E G,Martimez J M.A spectral conjugate gradient method for unconstrained optimization[J].Appl Math Optim,2001,43:117128.

[2]Zhang Li,Zhou Weijun,Li Donghui.Global convergence of a modified Fletcher-Reeves conjugate gradient method with Armijo-type line search[J].Numerische Mathematik,2006(104):561-572.

[3]Dai Zhifeng.Global convergence of some modified PRP nonlinear conjugate gradient methods[J].Optim Lett,2011(5):615-630.

[4]Zhang Li,Zhou Weijun,Li Donghui.A descent modified Polar-Ribiere and Polyak conjugate gradient method with armijo-type line search[J].IMA Journal of Numerical Analysis,2006(26):629-640.

[5]孟继东,杜学武.Armijo型线搜索一个修正LS共轭梯度法的全局收敛性[J].重庆师范大学学报,2012,11:6-8.

[6]Zhang Li,Zhou W,Li D.Some descent three-term conjugate gradient methods and their global convergence[J].Optim.Methods Softw,2007(22):697-711.

[7]张霞.一个新的光滑低阶精确罚函数[J].重庆工商大学学报:自然科学版,2013,30(8):36-38.

[8]李晓峰.修正的LS共轭梯度法在Armijo型线搜索下的全局收敛性[J].太原科技大学学报,2010,31(4):317-319.