CJ46型自升式钻井平台稳性计算方法研究
2015-04-24李春辉王钰涵
尹 艳, 莫 建, 李春辉, 王 超, 王钰涵
(上海外高桥造船有限公司, 上海 200137)
CJ46型自升式钻井平台稳性计算方法研究
尹 艳, 莫 建, 李春辉, 王 超, 王钰涵
(上海外高桥造船有限公司, 上海 200137)
该文在分析了风倾力矩、完整稳性和破舱稳性计算方法的基础上,重点对桩腿的等效计算方法展开研究,得到了准确的风倾力矩计算方法。为验证稳性计算方法的准确性,应用NAPA软件对某375英尺CJ46型自升式钻井平台的完整稳性和破舱稳性进行计算分析,阐述了风模型的建立、吃水和风向角的选取,以及初始重心高度的设定等关键问题。计算结果与基本设计进行了对比分析,证实了稳性计算方法的合理性和可靠性。
自升式钻井平台; 稳性; NAPA; 风模型
0 前言
自升式钻井平台不受风、浪、流等环境因素的影响而产生垂向升沉运动、纵向摇摆和横向漂移运动,相对于半潜式钻井平台和钻井船等移动平台自升式钻井平台居住舒适性更高。同时,自升式钻井平台又具有良好的移动性能,利用率高,因此目前自升式钻井平台被广泛应用。但是,在拖航情况下,自升式平台升起的桩腿不仅使得平台重心升高,还导致受风面积显著增大,直接影响自升式钻井平台稳性。在海洋平台设计过程中,必须准确预报风倾力矩,保证稳性计算结果满足衡准要求,因此研究自升式钻井平台稳性计算方法显得尤为重要。
1 风倾力矩
稳性计算的要点是确定平台受到的风倾力矩的大小,这是因为不论是平台的完整稳性还是破损稳性,都是自身的复原力矩抵抗风倾力矩的能力。
风荷载和风倾力矩可以根据式(1)、式(2)进行计算:
式中:F为风荷载;CS为受风构件的形状系数;CH为受风构件的高度系数;ρ为空气密度;V为风速;A为正浮或倾斜状态下所有暴露面的正投影面积;Z为风力作用力臂。

图1 桁架式桩腿的一个节距
为得到准确的风载荷和风倾力矩,关键是确定受风构件的形状系数和受风面积。平台甲板上有较多构件,但在风载荷模型建立过程中,主要建立主船体、井架、悬臂梁、钻台、吊机、桩腿以及上层建筑等模型。对于一些很难准确模拟的结构,采取相应的等效方式进行建模,例如井架采用板进行建模,取满实投影面积的60%;而吊机的吊臂可以等效为圆台,取满实投影面积的60%,其中最为关键的是把桁架式桩腿等效为圆柱。
不论是X型,K型还是双K型桁架式桩腿都是由大量的撑杆组成,如水平杆、斜撑、内撑杆以及弦杆等,K型桩腿节距结构如图1所示。因此在建立风模型时,为了方便建模,通常把桁架式桩腿转化为圆柱[1]。
等效桩腿直径De和等效拖曳力系数CDe按下式计算:
式中:di为第i个构件的直径;li为第i个构件的长度;L为节距。
式中:CDi为第i个构件的拖曳力系数,参考SNAME规范;li′为第个构件的投影长度;αi为风向与第i个构件投影到水平面线之间的夹角;βi为第i个构件为水平杆件之间的夹角。
2 稳性衡准
2.1 完整稳性衡准
在拖航过程中,平台需要足够的稳性来承受近海拖航工况(70 kn)和远洋拖航工况(100 kn)下360°方向的风荷载作用。目前,ABS和IMO MODU以及CCS等对稳性衡准都有规定,该文主要参考国际海事组织( IMO) 颁布的《海上移动式钻井平台构造和设备规则 2009》( MODU Code 2009)[2]。
自升式平台在各种作业工况下的完整稳性均应符合以下标准:
(1)至第二交点或进水角处的复原力矩曲线下的面积中的较小者,至少应比同一限定角处风倾力矩曲线下面积大40%;
(2)复原力矩曲线从正浮至第二交点的所有角度范围内均应为正值。
完整稳性曲线如图2所示。

图2 完整稳性曲线 图3 碰撞破损稳性曲线
2.2 破损稳性衡准
在计算破损稳性时,主要在一系列吃水情况下,考虑不同舱室破损后,受到50 kn风速的外部荷载,平台稳性是否仍能满足稳性衡准要求。
2.2.1 碰撞破损稳性
进水后的最终水线应在任何向下进水的开口下缘以下,进水点必须在复原力矩和风倾力矩的第一个交点之后,如图3所示。

图4 剩余稳性曲线
2.2.2 剩余稳性
国际海事组织(IMO) 颁布的《海上移动式钻井平台构造和设备规则 2009》( MODU Code 2009) 中新增了自升式平台单舱破损后剩余稳性的标准。
对于任何一个舱室的破损,自升式平台都必须有足够的稳性,且满足如下衡准要求:
式中:Ros=θm-θs,为稳性范围;θm为最大正稳性角;θs为破损后的稳定倾斜角。
剩余稳性曲线如图4所示。
3 进水点定义
非保护性开口、设有风雨密关闭装置的开口以及设有水密关闭装置的开口,这3大类开口是根据风雨密完整性和水密完整性划分的[3]。
在稳件计算中主要考虑平台的外部开口,其中完整稳性进水点主要考虑非保护性开口,而破损稳性进水点主要考虑风雨密开口以及非保护性开口。
4 工程计算实例
4.1 平台主要参数
该文选取CJ46型自升式平台,采用NAPA 软件对自升式钻井平台进行稳性分析,平台主要物理参数见表1。

表1 自升式平台主要参数
4.2 计算模型
该文采用NAPA软件进行建模和计算,在计算过程中,需要建立自升式钻井平台的静水力模型和风模型,如图5、图6所示。平台的浮态和复原力矩通过静水力模型计算得到,而计算自升式平台所受的风倾力矩关键是建立合适的风模型,风模型一旦建好,软件会根据风向计算出各个构件的受风面积以及压力中心,进行求和得到风倾力矩。
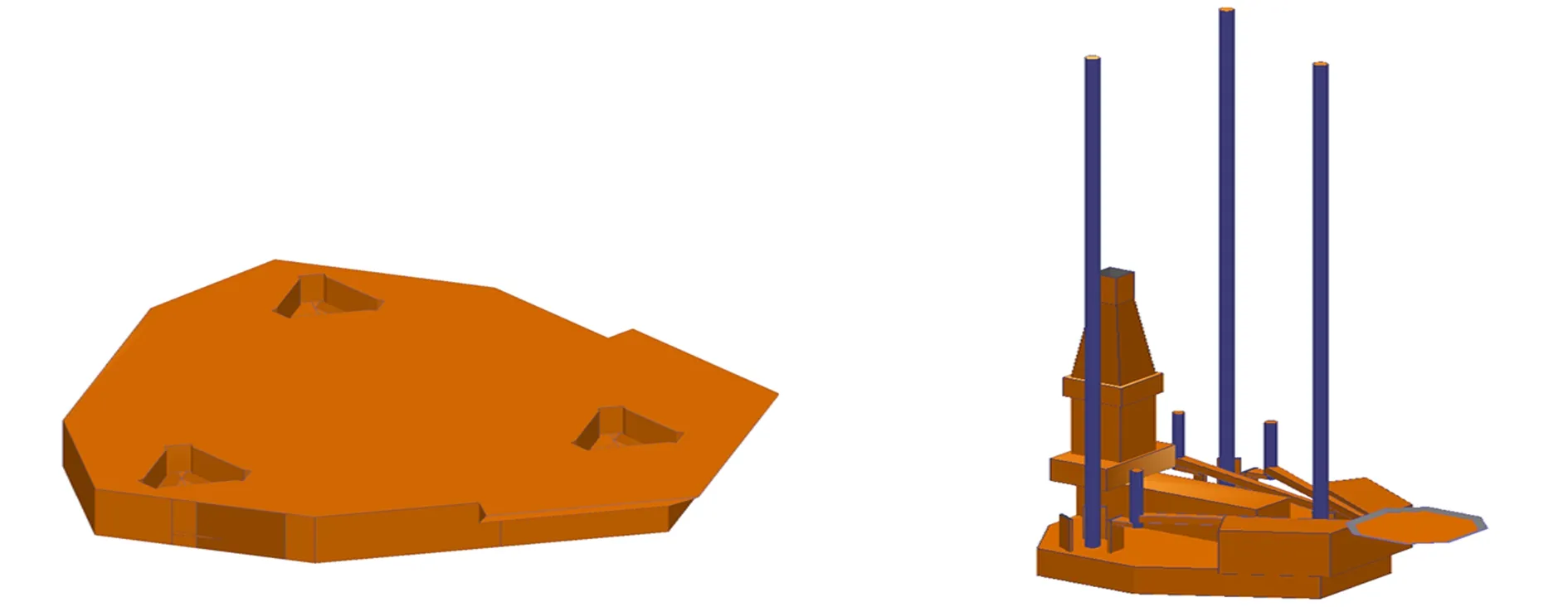
图5 静水力模型 图6 风模型
自升式钻井平台外形轮廓比较特殊,计算稳性和风倾力矩时需要考虑360°方向,然后求出最危险角度下的极限重心高。在计算过程中一旦出现稳性衡准问题,应该适度降低初始重心再次进行计算;反之在所有横倾角度下稳性都满足标准且留有裕度,则应该适度提高初始重心高,反复进行计算,直至求出与标准值无限接近的极限重心高。
定义破损舱室是计算破损稳性的关键,该舱室破损范围主要根据相关船级社规范要求以及舱室水密完整性进行定义划分。由于该平台尺寸比较对称,可单
独选取左舷或右舷,然后再进行破损舱组定义,且通过计算表明,边舱破损对许用重心高起决定性作用。
针对于自升式钻井平台近海拖航和远洋拖航两种海况,按照规范规定,分别采用70 kn和100 kn风速计算平台的完整稳性,采用50 kn风速进行破损稳性计算,稳性计算中最小风速要求见表2。

表2 稳性计算中最小风速要求
其中桁架式桩腿一般等效为圆柱,为了计算结果保守,考虑选取投影面最大的情况,此时风向垂直于桩腿面,选取桩腿中一节距如图7所示,该X型桩腿由3根弦杆、3根内撑杆以及6根斜撑杆组成,其中弦杆等效直径选取如图8所示,桩腿等效直径和等效拖曳力系数计算结果见表3、表4。

图7 选取的节距图 图8 弦杆的等效直径
表3 桩腿等效直径计算
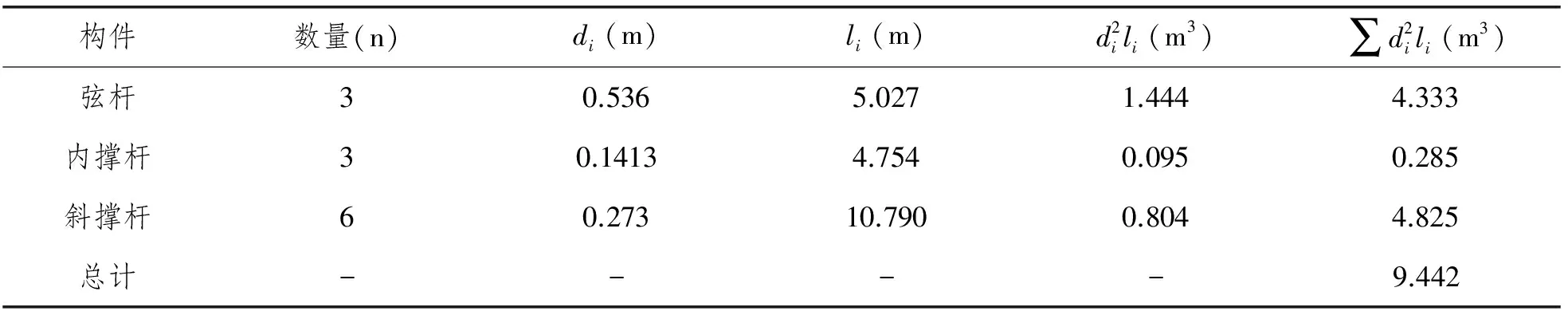
构件数量(n)di(m)li(m)d2ili(m3)∑d2ili(m3)弦杆30.5365.0271.4444.333内撑杆30.14134.7540.0950.285斜撑杆60.27310.7900.8044.825总计----9.442

表4 等效拖曳力系数
4.3 计算结果
该自升式平台的吃水范围定在4.0 m~5.0 m之间,由于平台左右舷基本对称,选取方向角为0°~180°,且以15°为一个间隔进行计算。通过计算,可以得到在近海拖航和远洋拖航两种工况下,平台完整稳性的许用重心高,见表5。

表5 各工况完整稳性下的许用重心高
该文选取边舱破损作为破舱组,由于该平台在近海和远洋拖航工况下的稳性计算均在50 kn风速下进行。根据工程实际操作,无论是远洋拖航还是近海拖航,桩腿一样长,因此得到的破舱稳性许用重心高一致,各工况破舱稳性下的许用重心高见表6。

表6 各工况破舱稳性下的许用重心高
剩余稳性只与平台自身破损后的抗倾覆能力有关,与进水点设置以及风倾力矩无关,因此在两种拖航情况下,平台剩余稳性许用重心高也是一致的,各工况剩余稳性下的许用重心高见表7。
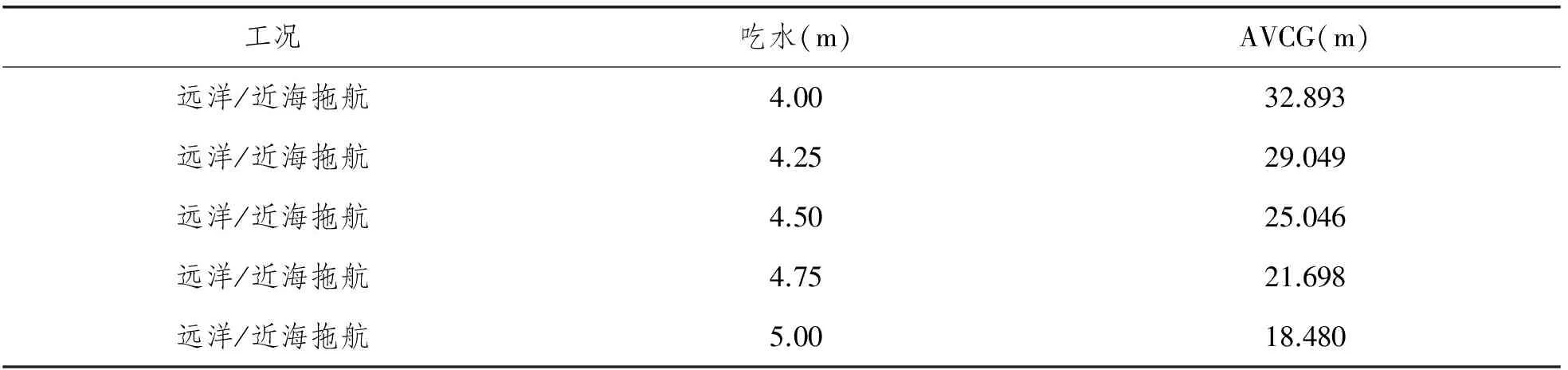
表7 各工况剩余稳性下的许用重心高
图9为自升式钻井平台在远洋和近海两种海况下的许用重心高度曲线(ACCG)。
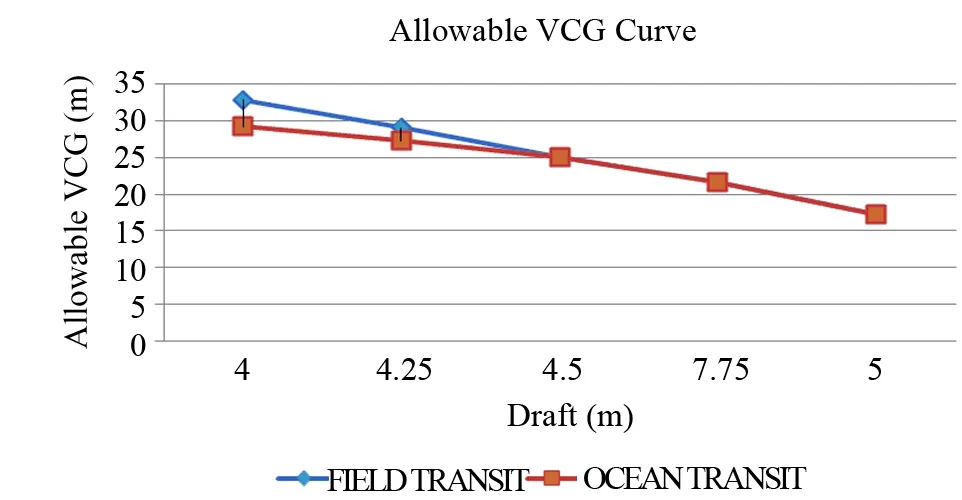
图9 许用重心高度曲线
5 结论
通过对CJ46型自升式钻井平台完整稳性和破损稳性计算分析,以及与基本设计进行对比,可得如下结论:
(1) 平台稳性计算较常规船舶而言,计算较为复杂。
(2) 风倾力矩对稳性的计算有着重要的意义,其中受风构件和形状系数是关键,因此桁架式桩腿等效技术显得尤为重要。
(3) 软件NAPA不能考虑遮蔽效应,因此得到的风载荷较为保守,对于平台安全性而言是有利的。
(4) 残余稳性只与平台破损后自身的抗倾覆能力有关,在计算时不需要考虑风倾力矩和进水点。
(5) 许用重心高度曲线是平台稳性结果的直接反应。
[1] SNAME. Guidelines For Site Specific Assessment of Mobile Jack-up Unites[S].2002.
[2] IMO. Code for the construction and equipment of mobile offshore drilling unit[S].2009.
[3] 刘海霞. 深水半潜式钻井平台的稳性分析[J]. 中国海洋平台, 2013, 28(6):5-11.
Analysis on the Stability Calculation of CJ46
Self-elevating Drilling Rig
YIN Yan, MO Jian, LI Chun-hui, WANG Chao, WANG Yu-han
(Shanghai Waigaoqiao Shipbuilding Co., Ltd, Shanghai 200137, China)
On the analysis of the wind heeling moments and the intact and damage stability calculation, the paper focused on the equivalent calculation method of leg, then we got the accurate calculating method of the wind heeling moments. In order to verify the accuracy of the stability calculation method, the paper calculate the intact stability and damage stability of a 375 ft jack-up drilling rig by NAPA software. The key points were modeling of wind profile, draft ,interval of azimuth angles and the initial height of the center of gravity. By being compared with the basic design, we confirmed the rationality and reliability of this method.
self-elevating drilling rig; stability; NAPA; wind model
2015-03-29
尹 艳(1988-),女,助理工程师。
1001-4500(2015)03-0035-06
P75
A
