任意齿差滚动活齿传动压力角计算方法及其影响因素分析*

宜亚丽 刘朋朋 金贺荣

(燕山大学机械工程学院，河北 秦皇岛 066004)

滚动活齿传动具有结构紧凑、传动比大、承载能力强和传动效率高等特点，在航空航天、数控机床、医疗器械等领域具有良好的应用前景［1］。一齿差滚动活齿传动通常采用偏心圆激波器，需进行动平衡处理。李瑰贤等［2］建立了偏心圆滚动活齿传动的力学模型，推导了滚柱活齿传动机构各构件的受力计算公式;Krylov N.V.［3］对偏心圆滚动活齿传动进行强度分析，得到了应力和应变的分布情况。

多齿差滚动活齿传动装置为几何轴对称结构，在传动过程中易实现整机静、动态受力自平衡，避免传动系统的振动激励，成为活齿传动领域的研究热点。董新蕊等［4］提出凸轮激波复式滚动活齿传动装置，对其传动原理、传动比及传动特性进行了分析;MIZUKAMI等［5-6］提出了一种活动销输入型摆线凸轮多齿差滚动活齿传动机构;梁尚明等［7］将优化设计理论与稳健设计方法相结合，建立了二齿差滚动活齿传动的多目标稳健优化设计数学模型;黄劲枝等［8］对激波器和中心轮齿廓均采用余弦类曲线的任意齿差数纯滚动活齿传动进行了研究。宜亚丽等［9］采用无刚性、柔性冲击的5 次多项式类曲线的齿形模型，实现了滚动活齿任意齿差等速共轭传动。

压力角作为衡量活齿机构传动性能的重要参数，其大小影响着机构的受力状况、传动效率及工作可靠性，研究压力角变化规律及其影响因素对于指导活齿传动设计具有重要意义。本文建立多类齿形统一齿廓方程，推导出滚动活齿传动机构压力角解析式，分析不同齿形滚动活齿传动机构压力角的变化规律，确定压力角的影响因素。

1 滚动活齿传动原理

如图1 所示，滚动活齿传动由激波器、活齿、活齿架和中心轮组成，激波器和中心轮齿廓曲线按照给定的运动规律和传动比确定，其中活齿由活齿轴和滚动轴承组成，通过滚动轴承使组成高副的两运动副元素间形成局部自由度，实现激波器齿廓、中心轮齿廓、活齿槽与活齿的纯滚动接触啮合。Ⅰ类传动形式为活齿架固定，激波器输入，中心轮输出。激波器匀速旋转时，活齿中心始终处于激波器理论廓线与中心轮理论廓线交点位置处并沿活齿架的活齿槽作径向运动，推动中心轮转动输出。Ⅱ类传动形式为中心轮固定，激波器输入，活齿架输出。

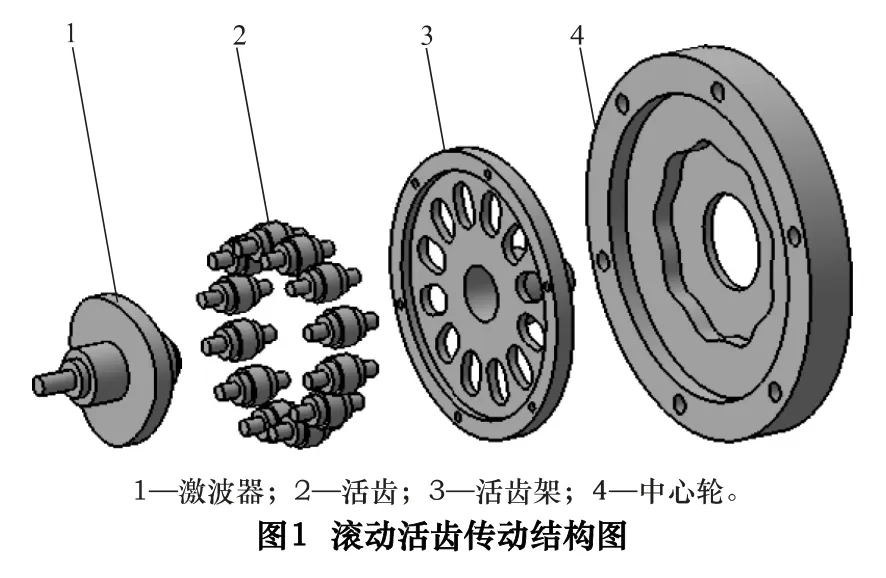
2 齿廓方程建立

选定活齿运动规律即可设计出满足要求的激波器齿廓和中心轮齿廓，常用的活齿运动规律有偏心圆类曲线、椭圆类曲线、余弦类曲线和高次多项式类曲线等。文中各符号含义如表1 所示。

表1 滚动活齿传动各符号含义

2.1 活齿的运动规律

图2 为偏心圆激波器齿形，由余弦定理知

于是可得

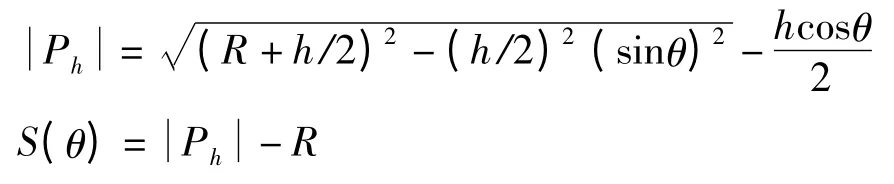
偏心圆类齿形活齿运动规律为

图3 为椭圆激波器齿形，由椭圆参数方程知

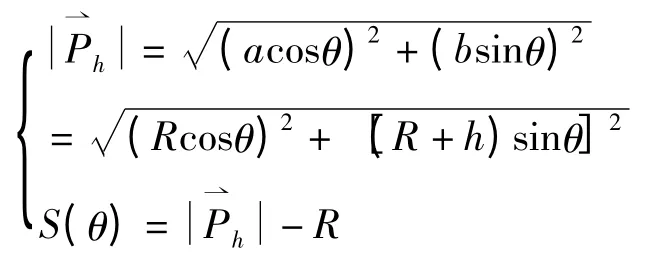
椭圆类齿形活齿运动规律为

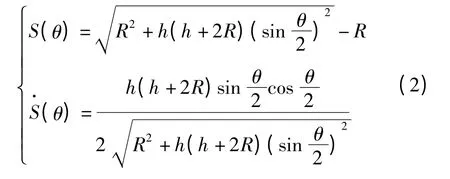
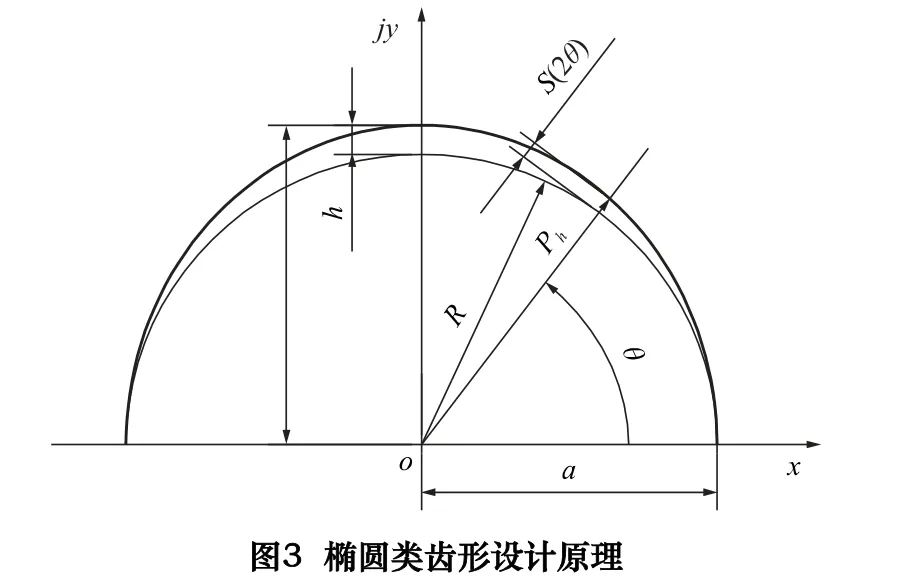
式中:a 为椭圆短半轴;b 为椭圆长半轴;h=b -a;R=a。

如图4 所示，余弦类齿形活齿运动规律为

高次多项式类齿形活齿推程运动规律为

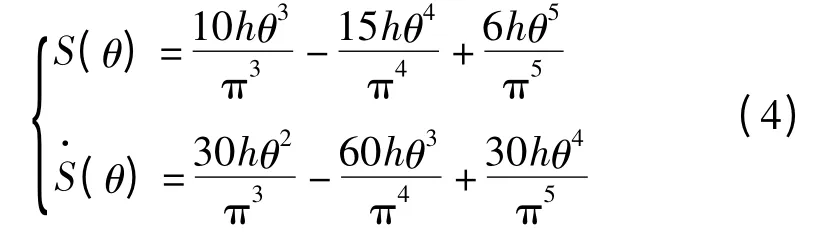
回程运动规律为

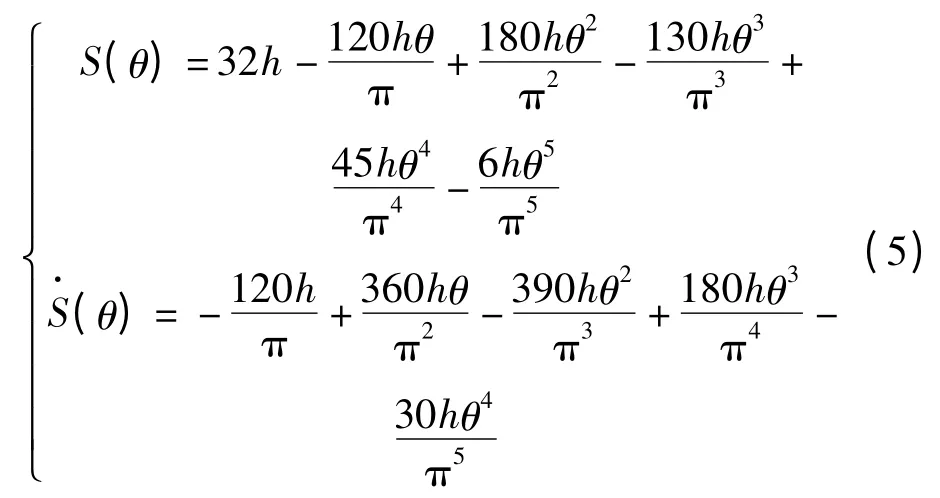
2.2 齿廓方程

图2～4 中θ∈［0，π/Zh］为活齿的推程，θ∈［π/Zh，2π/Zh］为活齿的回程。不同齿形激波器理论廓线方程统一为

其展开式为

对向量Ph求导得

不同齿形中心轮理论廓线方程统一为

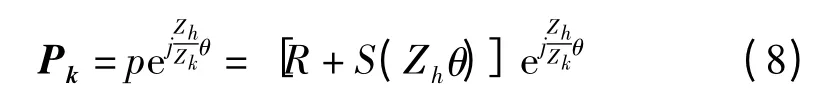
其展开式为

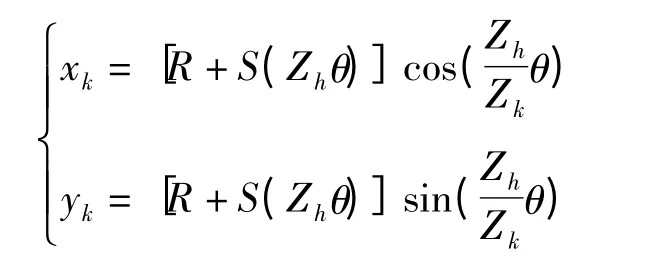
对向量Pk求导得

3 机构压力角解析

在传动机构运转过程中，影响机械动力特性的一个主要因素是齿廓曲线接触点处的压力角，即接触点处所受的法向力(与齿廓对应点的公法线方向一致)与该点速度方向所夹的锐角［10］。

如图5 所示，Ⅰ类传动形式中，激波器与活齿间啮合压力角α1为激波器对活齿法向作用力方向与活齿运动方向间所夹锐角;活齿与中心轮间压力角α2为活齿对中心轮法向作用力方向与中心轮运动方向间所夹锐角。

Ⅱ类传动形式中，激波器与活齿间压力角α3为激波器对活齿法向作用力方向与活齿运动方向间所夹锐角;活齿与活齿架间压力角α4为活齿对活齿架法向作用力方向与活齿架运动方向间所夹锐角，大小始终为零。

激波器与活齿间啮合压力角α1为

活齿与中心轮间的啮合压力角α2为

激波器与活齿间啮合压力角α3为

活齿与活齿架间的啮合压力角α4

由式(7)和式(9)可得滚动活齿传动激波器、中心轮齿廓的切线方向角分别为

由反正切函数值域知，φ∈(-π/2，π/2)，第一象限内，当φ∈(-π/2，0)时，在arctan 的主值上加π;第二象限内，当φ∈(0，π/2)时，在arctan 的主值上加π。

4 仿真与分析

滚动活齿传动齿形参数如表2 所示，根据表2 中数据进行实例仿真。

表2 滚动活齿传动齿形参数

活齿传动是多齿啮合传动，一、二、三齿差活齿传动的一个推程啮合周期分别为180°、90°和60°。根据表2 参数，以一齿差偏心圆类为例，绘制一个推程啮合区4 个并联活齿的压力角α1、α2、α3的示意图，4 个并联活齿编号依次为①、②、③、④，啮合相位差为45°，如图6 所示。同理，二齿差椭圆类一个推程啮合区有4 个并联活齿，4 个并联活齿编号依次为①、②、③、④，啮合活齿的相位差为22.5°;三齿差余弦类和多项式类一个推程啮合区有3 个并联活齿，3 个并联活齿编号依次为①、②、③，啮合活齿的相位差为20°。多活齿并联啮合协同工作，重合度高，使活齿传动具有较强的承载力和抗冲击载荷的能力，传动平稳、噪声小。

4.1 Ⅰ类传动形式

Ⅰ类传动形式中激波器与活齿间的啮合压力角α1的变化曲线如图7 所示。

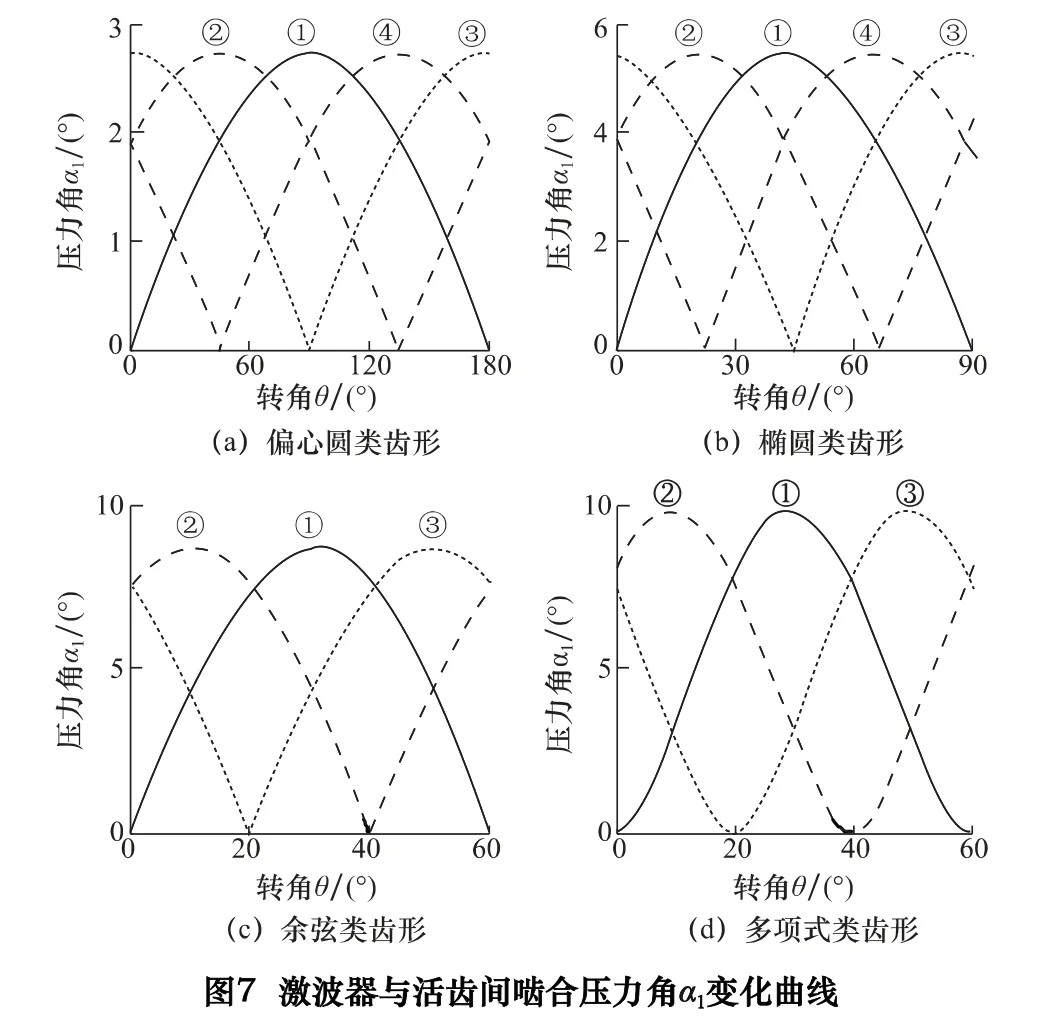
随着激波器转动，α1不断变化且变化平缓，开始从0°变化到最大值α1max，然后又从最大值α1max变化到0°，在推程的起点和终点压力角α1为0°，显然最大值α1max越小，对传动越有利。一齿差偏心圆类α1max=2.7°最小，其次是二齿差椭圆类α1max=5.5°，三齿差余弦类α1max=8.5°和三齿差多项式类α1max=9.7°，相对于一、二齿差滚动活齿传动较大些，但最大值α1max仍然较小，保证激波器与活齿间啮合传力性能。

由式(10)知α1max与齿形参数R、h 和Zh有关。改变h/R，保持其他参数不变，可得压力角α1max随h/R的变化曲线，如图8a 所示，压力角α1max随基圆半径R的增大而减小，随行程h 的增大而增大，α1max与h/R 成线性关系，随h/R 的增大而增大;改变激波器齿数Zh，保持其他参数不变，可得压力角α1max随激波器齿数Zh的变化曲线，如图8b 所示，压力角α1max与激波器齿数Zh基本成线性关系，随激波器齿数Zh的增大而增大。

活齿与中心轮间的啮合压力角α2的变化曲线如图9 所示。随激波器转动，α2不断变化且变化平缓，开始从90°变化到最小值，然后又从最小值变化到90°，在推程的起点和终点压力角为90°，最小值α2min越小，对传动越有利。一齿差偏心圆类活齿传动α2min=68.0°，二齿差椭圆类活齿传动α2min=57.5°，三齿差余弦类活齿传动α2min=54.4°，三齿差多项式类活齿传动α2min=50.0°。滚动活齿传动是多齿啮合传动且压力角α2变化存在相位差，活齿与中心轮间的压力角α2可满足传动要求。

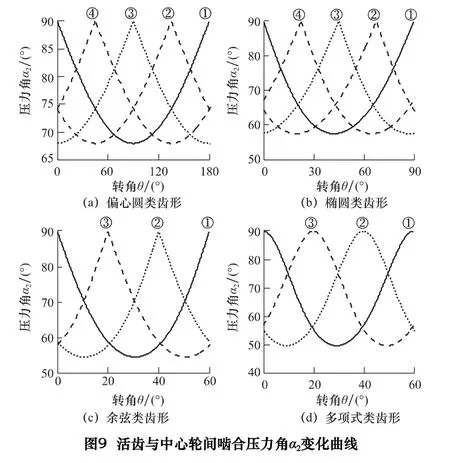
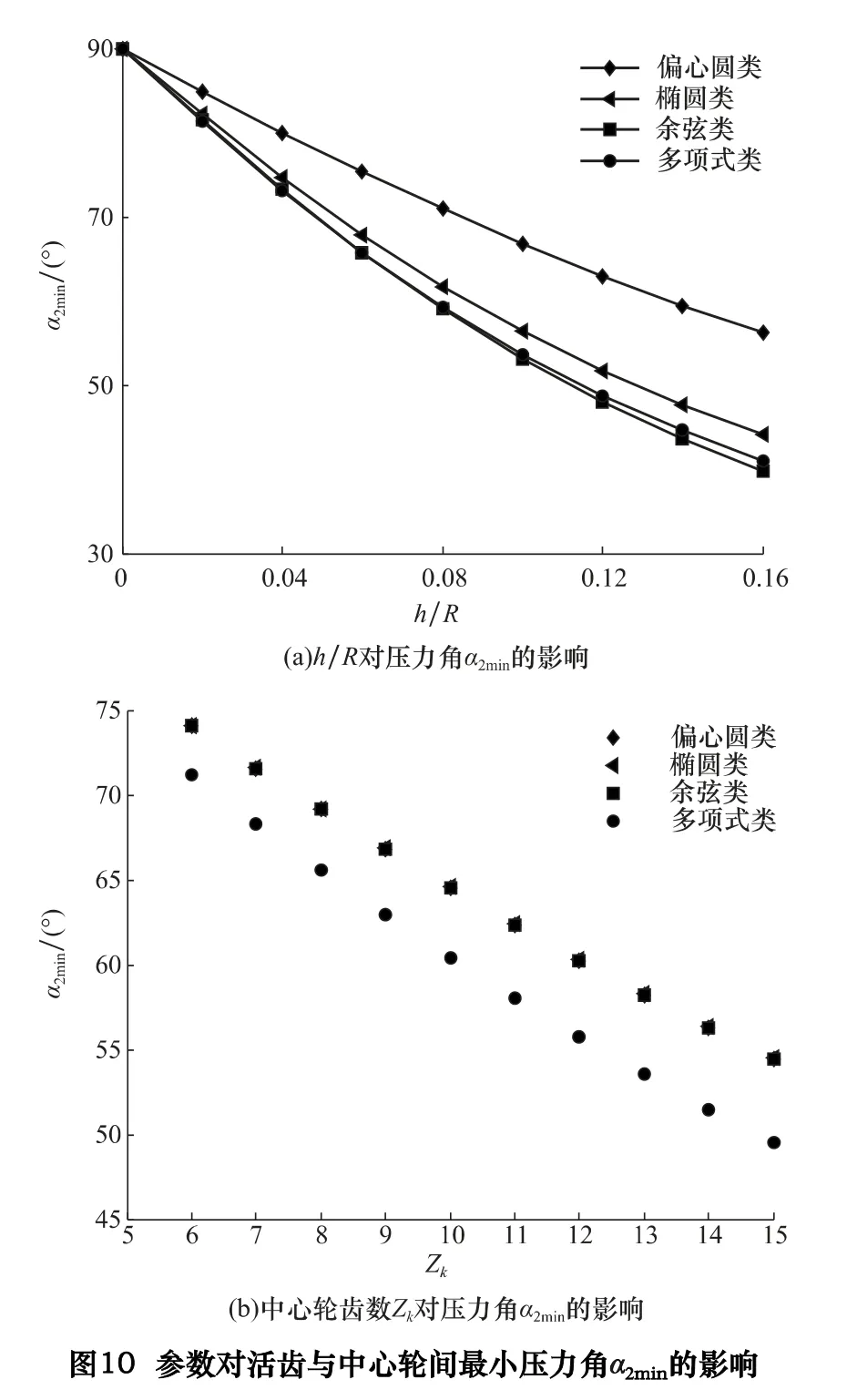
改变h/R，保持其他参数不变，可得压力角α2min随h/R 的变化曲线，如图10a 所示，压力角α2min随基圆半径R 的增大而增大，随行程h 的增大而减小，α2min与h/R 近似成线性关系，随h/R 的增大而减小。

改变激波器齿数Zk，保持其他参数不变，压力角α2min随中心轮齿数Zk的变化曲线如图10b 所示，压力角α2min与中心轮齿数Zk基本成线性关系，随中心轮齿数Zk的增大而减小。显然，参数对α1max和α2min的影响恰好相反，无法同时获得最小的α1max和α2min。当活齿架固定，激波器输入，中心轮输出时，考虑到α1在0°到α1max之间变化且值较小，α2在α2min和90°之间变化且值较大，所以选择齿形参数时，应主要考虑参数对中心轮与活齿间最小压力角α2min的影响。

4.2 Ⅱ类传动形式

Ⅱ类传动形式中激波器与活齿间的啮合压力角α3的变化曲线如图11 所示。随激波器转动，α3不断变化且变化平缓，开始从90°变化到最小值α3min，然后又从最小值α3min变化到90°，在推程的起点和终点压力角为90°，最小值α3min越小，对传动越有利。一齿差偏心圆类α3min=69.5°最大，其次是二齿差椭圆类α3min=61.5°和三齿差余弦类α3min=62.5°，三齿差多项式类α3min=59.0°，相对于其他类滚动活齿传动较小些，激波器与活齿间传力性能较好。多活齿啮合存在相位差，并联协同工作可满足传动要求。

由于活齿与活齿架间压力角α4随激波器的转动保持不变且时刻为零，当中心轮固定，激波器输入，活齿架输出时，选择齿形参数只需考虑参数对激波器与活齿间最小压力角α3min的影响。

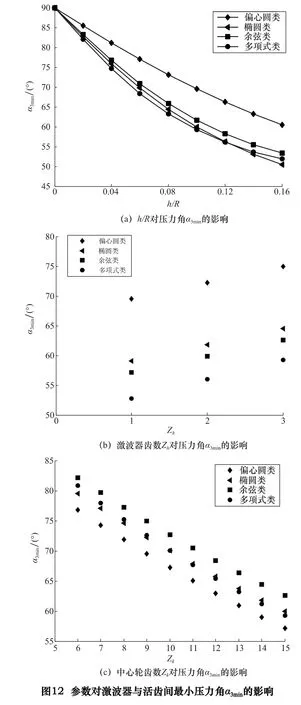
改变h/R，保持其他参数不变，可得压力角α3min随h/R 的变化曲线如图12a 所示，压力角α3min随基圆半径R 的增大而增大，随行程h 的增大而减小，α3min与h/R 近似成线性关系，随h/R 的增大而减小;改变激波器齿数Zh，保持其他参数不变，可得压力角α3min随激波器齿数Zh的变化曲线如图12b 所示，压力角α3min与激波器齿数Zh基本成线性关系，随激波器齿数Zh的增大而增大;压力角α3min随中心轮齿数Zk的变化曲线如图12c 所示，压力角α3min与中心轮齿数Zk基本成线性关系，随中心轮齿数Zk的增大而减小。

5 结语

(1)活齿啮合压力角α1、α2、α3的大小都随活齿转角的变化而变化，不同时刻压力角不同且压力角的极值一般发生在啮合过程的中点;活齿压力角α4不随活齿转角的变化而变化，且时刻为零。

(2)基圆半径R、行程h、激波器齿数Zh和中心轮齿数Zk都会影响活齿机构压力角的大小，不同活齿传动齿形下，机构压力角的变化规律不同，但变化趋势相同。压力角α1max随h/R 的增大而增大，随Zh的增大而增大;压力角α2min和α3min随h/R 的增大而减小，随Zk的增大而减小;压力角α3min随Zh的增大而增大。

(3)建立不同类型齿形廓线方程的统一数学表达式，有助于针对活齿运动规律不同的任意齿差滚动活齿机构开展功能和性能的后续研究工作。

［1］曲继方.活齿传动理论［M］.北京:机械工业出版社，1993.

［2］李瑰贤，杨伟君，顾晓华.滚柱活齿传动受力分析的研究［J］.机械设计，2002，19(1):18 -20.

［3］Krylov NV.Strength analysis of wave gear with intermediate rolling bodies with rotational motion of the output link［J］.Trudy MAI，2013，65:1 -15.

［4］董新蕊，李剑锋，王新华，等.凸轮激波复式活齿传动的结构及齿形分析［J］.中国机械工程，2006，17(16):1661 -1665.

［5］Masami Mizukami，Hidetsugu Terada.Study on movable pins input type trochoid gear reducer(1st Report)［J］.Japan Society for Precision Engineering，2009，75(11):1335 -1339.

［6］Masami Mizukam，Hidetsugu Terada.Study on movable pins input type trochoid gear reducer(2st Report)［J］.Japan Society for Precision Engineering，2010，76(6):663 -667.

［7］梁尚明，孙强，姚进.二齿差滚动活齿传动多目标稳健优化设计［J］.西南交通大学学报，2012，47(2):241 -244.

［8］黄劲枝，程时甘，陈贤湘.任意齿差数纯滚动活齿传动［J］.机械设计与研究，2008，24(4):44 -46.

［9］宜亚丽，刘朋朋，安子军，等.任意齿差推杆活齿高次多项式曲线齿廓齿形研究［J］.机械传动，2014，38(4):1 -4.

［10］杨玮，曹巨江.弧面凸轮机构的压力角和曲率分析［J］.机械科学与技术，2004，23(1):74 -76.