一种单喷管双摆电动伺服系统的设计与建模
2015-04-24高智刚张佼龙
高智刚,张佼龙,周 军,李 朋
(西北工业大学 精确制导与控制研究所,西安 710072)
一种单喷管双摆电动伺服系统的设计与建模
高智刚,张佼龙,周 军,李 朋
(西北工业大学 精确制导与控制研究所,西安 710072)
针对新型战术导弹对摆动喷管伺服系统提出的小型化大功率要求,提出了一种基于电动伺服系统的单喷管双摆驱动装置。该装置使用2个相互垂直的直线式电动伺服机构共同推动喷管进行摆动,采用无刷直流电机和滚珠丝杠减速器的结构形式,实现了系统的高功率密度和高效率,可提供大输出力矩,并具有良好控制精度。通过对该系统进行运动分析与建模,研究了2个直线式电动伺服机构的运动非线性特性及相互间交连耦合干扰,分析了两者的成因、随摆角分布规律及其对喷管摆动角位置精度的影响,给出了任意摆角下的双通道指令计算方法,据此采用双通道协同工作的方式精确控制喷管摆动方向和摆动角度。
摆动喷管;电动伺服系统;滚珠丝杠;无刷直流电机;运动非线性;交连耦合干扰
0 引言
以摆动喷管方式实现的推力矢量技术是导弹和火箭进行机动控制的有效手段。目前,国内外的大型运载火箭及弹道导弹主要采用电液伺服系统实现喷管摆动,取得了许多成功的应用[1]。但电液伺服系统结构复杂、体积较大、密封要求高,在保养维护等方面,也存在不便之处。同时,随着新型战术导弹对机动能力的要求不断提升,也开始采用摆动喷管式的推力矢量技术,但受限于小体积结构空间、低成本等约束,电液伺服系统已不能完全满足这一类的应用需求。
近年来,电动伺服技术取得了长足进步,在功率质量比、工作性能、可靠性等方面有了很大提高。特别是在千瓦级输出功率和千牛米级输出力矩等级,已达到可与电液伺服技术媲美的水平,而在体积重量、自身结构、保养维护、成本等方面,则更具有优势。在推力矢量控制、高超声速飞行器和再入返回飞行器等领域,均已使用大功率电动伺服系统作为执行机构[2-5]。因此,对新型战术导弹而言,使用电动伺服系统实现喷管摆动控制是一种切实可行的优异选择。
与四喷管式推力矢量系统相比,单喷管式推力矢量系统能有效减小结构质量和伺服装置数量,充分利用喷管周围空间[6]。因此,本文开展了单喷管双摆电动伺服系统的设计,提出了一种基于无刷直流电机和滚珠丝杠减速器的双通道小型大功率电动伺服系统方案,对2路相互垂直的直线电动伺服机构在控制喷管摆动过程中的运动非线性和交连耦合干扰进行研究,建立该系统数学模型,并进行仿真分析[7-9]。通过以上工作,验证使用电动伺服系统实现对喷管摆动方向和摆动角度精确控制的能力。
1 单喷管双摆电动伺服系统总体结构
对于单喷管双摆电动伺服系统,使用2个相互垂直的电动伺服机构,可使喷管作任意方向摆动,进而控制导弹在俯仰和偏航两个方向的运动。该系统基本结构如图1所示。
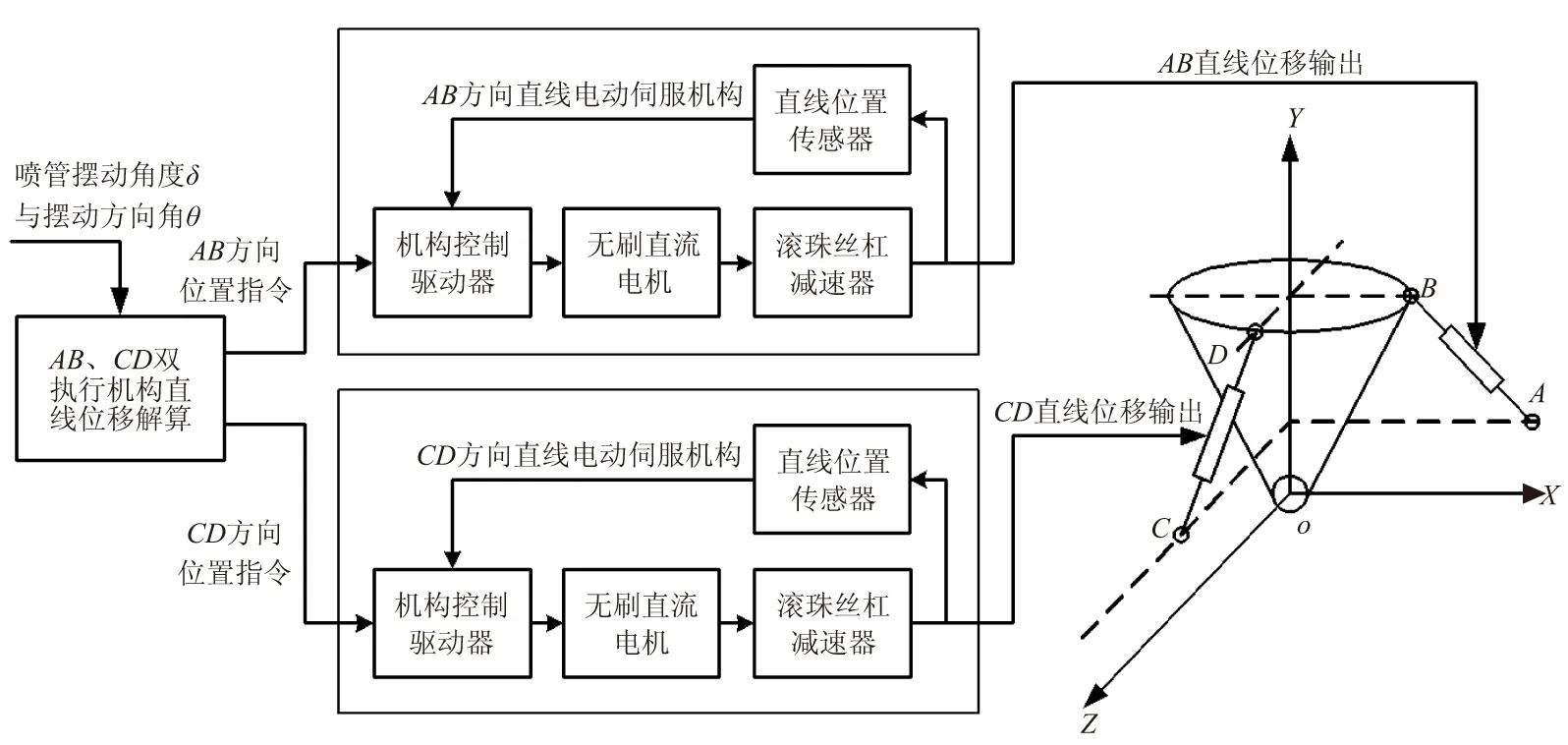
图1 单喷管双摆电动伺服系统结构示意图Fig.1 Structure of single nozzle-double pendulum electrical servo system
单喷管双摆电动伺服系统的组成如下:
(1) 双执行机构直线位移解算单元(AB方向、CD方向)。
(2)AB方向、CD方向的2套作动筒式直线电动伺服机构,包括电动伺服机构控制驱动器、无刷直流电机、滚珠丝杠减速器、直线位置传感器。
(3) 与喷管、弹体相连接的轴承支座,上下支耳均采用关节轴承,分别与舱壁、喷管壁上的支耳座连接。
该系统将输入的喷管摆动角δ和摆动方向角θ,解算为AB、CD两个方向的电动伺服机构直线位移量,送入两方向直线电动伺服机构。两者均为直线位置随动系统,由控制驱动器根据线位移指令和线位置反馈计算控制量,驱动电动伺服机构输出所需直线位移。由两方向直线位移的综合效果,即可控制喷管产生所需的摆动角δ和摆动方向角θ。
直线式电动伺服机构采用无刷直流电机+滚珠丝杠减速器的结构形式。作为实现能量转换、力放大与输出的两大核心元件,两者性能将直接决定电动伺服机构的最终输出性能。无刷直流电机具有功率密度大、散热性能好、工作寿命长等优点,滚珠丝杠减速器具有传动效率高、传动精度高、传动比大、便于转动-直线运动相互转换等优点,均是大功率直线输出电动伺服机构的良好选择。
该直线式电动伺服机构的工作方式为以无刷直流电机作为动力驱动元件,通过两级齿轮副,将伺服电机的转动传递给滚珠螺母;随后,在防转导向机构作用下,限制丝杠转动,使用螺母旋转-丝杠轴向移动的传动方式,输出所需直线运动。
2 单喷管双摆电动伺服系统运动分析
分析可知,若2个直线式电动伺服机构的下支点与喷管摆动中心在同一平面,则AB直线伺服机构在XOY平面内摆动喷管时,YOZ平面内的CD直线伺服机构无需改变输出直线位置,反之亦同。但通常受限于结构要求,电动伺服机构安装位置往往不能达到该理想位置,此时任一直线伺服机构沿自身所在垂直方向运动时,为了使喷管达到预定摆角,将会对另一方向的直线伺服机构产生线位移输出干扰,将这种扰动称为两直线伺服机构间的交连耦合干扰。为了提高喷管摆角的控制精度,需要分析两伺服机构间的交连耦合干扰特性。
设为图1所示一般位置,即下支点与喷管转动中心不在同一平面内,由摆动角方向分为沿两直线伺服机构相互垂直方向摆动和任意方向摆动。
(1) 首先,考虑喷管沿两直线伺服机构相互垂直方向摆动。以分析伺服机构AB、CD长度随喷管在XOY平面内摆动角度δ的变化关系为例,将所有结构尺寸投影到XOY平面,如图2所示。
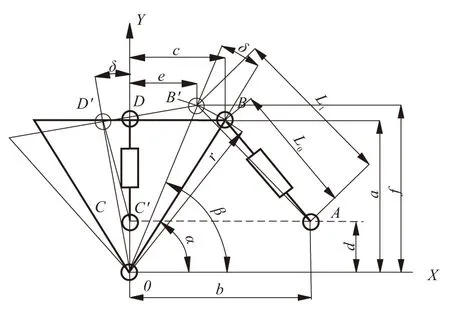
图2 单喷管双摆电动伺服系统XOY平面投影图Fig.2 Projection on XOY of single nozzle-double pendulum electrical servo system
可推导出,AB直线伺服机构长度与摆动角度δ的关系为
(1)
此时,两直线伺服机构之间存在交连耦合干扰,过D点做一个辅助平面PlaneA与XOY面平行。则推导可知,为了保证喷管摆动角度,CD直线伺服机构受AB直线伺服机构动作影响的扰动尺寸为
(2)
式中C′为过C点作平面PlaneA垂线的垂足。
(2) 当喷管沿任意方向摆动时,设摆动方向与X轴正方向夹角为θ,过B点作辅助平面PlaneB与摆动方向平行,如图3所示。推导此时AB、CD两直线伺服机构线位移与摆动角度δ间关系。
当喷管沿θ方向摆动角度δ时,AB直线伺服机构的长度变为
(3)
式中A′为过A点作平面PlaneB垂线的垂足。
同理,可得出CD直线伺服机构的长度变为
(4)

图3 单喷管双摆电动伺服系统任意方向摆动图Fig.3 Structure of single nozzle-double pendulum electrical servo system on random direction
3 摆动喷管电动伺服系统数学建模
3.1 摆动喷管电动伺服系统传动比
对于AB、CD直线式电动伺服机构,其滚珠丝杠减速器均为两级齿轮副+滚珠丝杠副的传动结构,可分别得到两者传动比,并计算滚珠丝杠减速器传动比,进而推导出摆动喷管直线伺服系统的总传动比。
二级齿轮副的传动比为
(5)
式中z1为与电机轴固连的主动齿轮齿数;z2为中间级从动齿轮齿数;z3为中间级主动齿轮齿数;z4为与滚珠螺母固连的从动齿轮齿数。
滚珠丝杠副的传动比为
ig=2π/p
(6)
式中p为滚珠丝杠导程。
故滚珠丝杠减速器的传动比为
(7)
对摆动喷管伺服系统而言,在负载力矩确定的情况下,摆动力臂的大小决定直线伺服机构输出力的负载特性,即F=M/R1。其中,M为负载力矩,F为直线伺服机构输出力,R1为摆动力臂。则对于AB直线伺服机构,设∠OAB′=γ,有
(8)
其中
可得伺服电机的驱动力矩为
(9)
故摆动喷管直线伺服机构的总传动比为
i=R1·ic·ig
(10)
3.2 无刷直流电机数学模型
无刷直流电机将绕组作为定子,由永磁体构成转子,通过检测转子位置,并按规律由驱动电路依次向三相绕组供电,从而驱动无刷直流电机进行转动。根据其结构,假设:
(1) 电机定子三相完全对称,空间上互差120°。
(2) 三相绕组采用Y型连接,且三相绕组的电阻、电感参数相同。
可得出由三相电压平衡方程、反电动势方程、电磁转矩方程和电机运动方程联立构成的无刷直流电机数学模型如下:
(11)
式中R为电机绕组相电阻;L为电机绕组相电感;M为绕组相间互感;Ke为反电动势系数;n为电机转速;Kt为电机转矩系数;Tm为电机负载转矩;J为转子转动惯量;B为摩擦系数。
4 仿真与分析
根据以上方程建立单喷管双摆电动伺服系统数学模型,根据所输入结构尺寸和技术指标要求,开展了单喷管双摆电动伺服系统设计,最终确定电机转速为12 000 r/min,二级齿轮副传动比为3.64,滚珠丝杠导程为6 mm。设计结果表明,该系统能够达到摆动喷管所需输出力矩、摆动角速度和最大摆角要求,体积重量也满足小型化、轻量化要求。
同时,利用该模型进行了单喷管双摆电动伺服系统运动仿真,仿真曲线如图4~图8所示。根据仿真结果,可看出:
(1) 在推动喷管进行正负偏转时,正、负向相同喷管摆角对应的直线伺服机构工作行程不同,且随着喷管摆角的增大,两个方向工作行程的不对称度会不断增大。由图4和图5可知,本系统中两方向最大行程偏差可达单方向总行程的5.1%。
(2) 由式(1)可知,AB、CD直线式电动伺服机构工作行程与喷管摆角之间为非线性关系。图6给出了本系统中两方向直线行程的非线性偏差(相对于摆角-直线行程线性拟合值),最大可达该方向行程的1.1%和0.3%。计算可知,若忽略此非线性因素影响,造成的喷管摆角偏差最大可达0.1°。
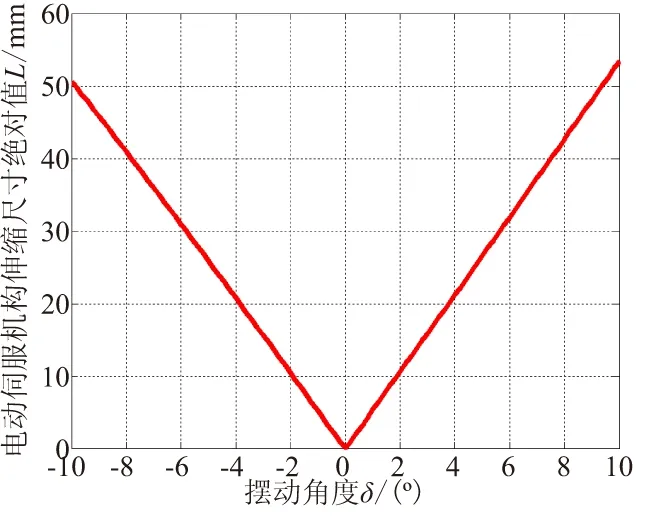
图4 伸缩长度绝对值随喷管摆角变化关系Fig.4 Expansion length(fabs) of AB/CD actuator vs swing angle δ
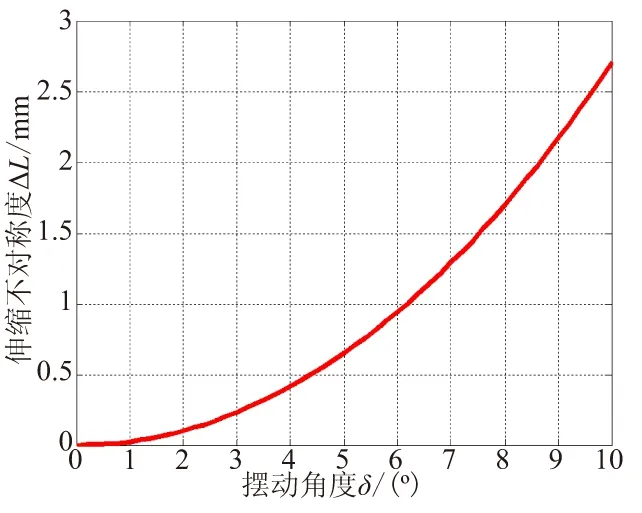
图5 伸缩长度不对称度随喷管摆角变化关系Fig.5 Asymmetry of expansion length vs swing angle δ
(3) 受电动伺服机构下支点相对于喷管摆动中心轴向距离的影响,当其中任意一个直线伺服机构沿自身所在方向推动喷管摆动时,会对另一垂直方向直线伺服机构的工作行程产生交连耦合干扰。从图7可看出,由于结构上的对称性,该交连耦合干扰对于喷管摆角的正负向变化具有对称性,但随摆角增加,该干扰不断增大,本系统中最大可达单方向总行程的2%。
若不对此线位移输出干扰进行补偿,会同时引起喷管摆动角度和摆动方向角出现偏差,造成喷管摆角减小,摆动方向角向被干扰电动伺服机构所在方向出现偏移。
(4) 由图8可知,随着摆动方向角不同,相同喷管摆角对应的AB、CD直线电动伺服机构工作行程各不相同。因此,需要根据喷管摆动角度δ和摆动方向角θ,利用式(3)和式(4),实时解算AB、CD直线伺服机构工作行程,同步控制两直线伺服机构协同工作,方能实现对喷管摆动角度和摆动方向的精确控制。
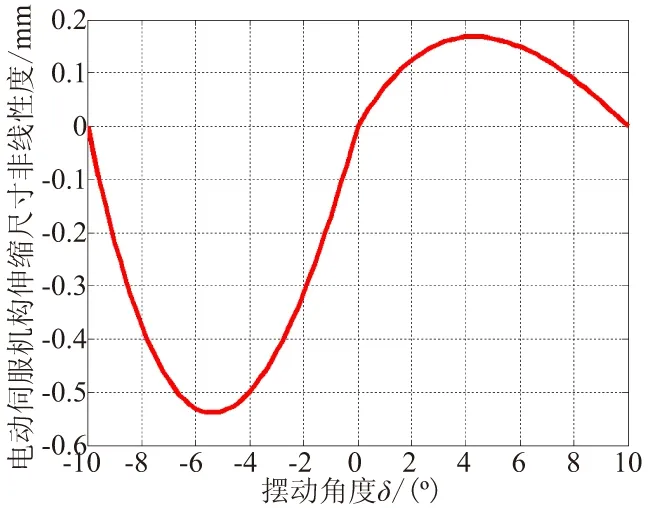
图6 电动伺服机构伸缩长度非线性度曲线Fig.6 Nonlinear characteristic of expansion length vs swing angle δ
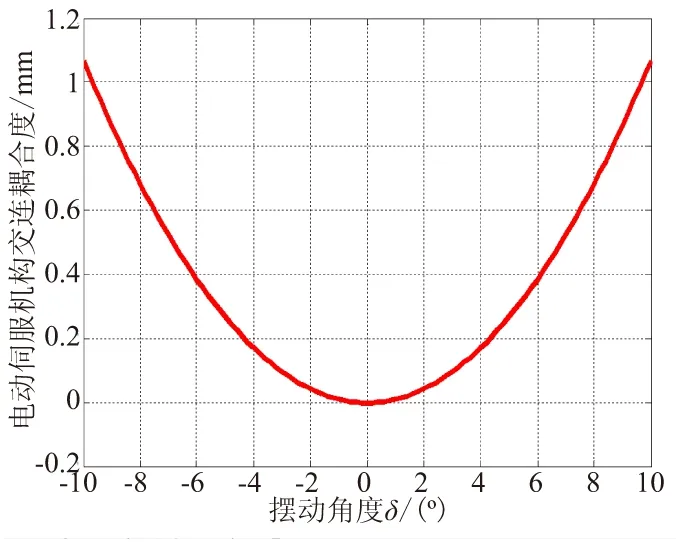
图7 电动伺服机构伸缩长度交连耦合曲线Fig.7 Cross-linked interference of expansion length vs swing angle δ
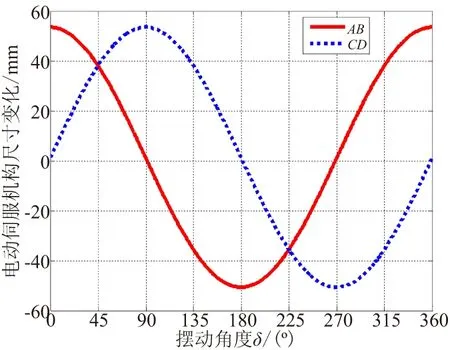
图8 喷管摆动时AB/CD电动伺服机构伸缩尺寸(δ=10°)Fig.8 Expansion length of AB/CD actuator vs swing direction angle θ(δ=10°)
根据以上仿真结果,可得:
(1) 摆动喷管电动伺服机构的运动非线性和正负向不对称是由于采用摇臂式结构造成的,而交连耦合干扰则受AB、CD电动伺服机构下支点与喷管摆动中心之间的轴向距离影响,该轴向距离越大,则交连耦合干扰越大。
(2) 所存在的运动非线性特性及相互间交连耦合干扰主要影响喷管摆动角度和摆动方向角的精确性,对喷管摆动速度、输出力矩的影响不明显。
(3) 驱动喷管沿任意方向摆动时,需根据第2章所列公式计算,并控制两直线伺服机构工作行程。
5 结论
(1) 采用无刷直流电机作为驱动元件,齿轮副完成传动比匹配,滚珠丝杠副作为大传动比传动机构的基本结构形式是单喷管双摆电动伺服系统最佳组合方式,能够满足战术导弹对摆动喷管伺服系统提出的小型化、高功率密度和高性能指标要求。
(2) 摆喷电动伺服系统所采用的摇臂式结构会造成直线伺服机构出现运动非线性和正负向不对称,而直线伺服机构下支点与喷管摆动中心的轴向距离差会引起两伺服机构间产生交连耦合干扰。在进行摆喷伺服系统控制指令计算时,应考虑以上因素的影响,否则会使得喷管摆角和摆动方向角的控制精度降低。
(3) 在推动喷管进行任意方向摆动时,为了实现对喷管摆动方向和摆动角度的精确控制,需解算两通道位置指令,并同步控制两直线伺服机构协同工作。
[1] 朱康武,傅俊勇,曾凡铨,等. 运载火箭电液推力矢量控制系统总体设计策略研究[J]. 宇航学报, 2014, 35(6): 685-692.
[2] Yohan Lin, Ethan Baumann, David M Bose, et al. Tests and techniques for characterizing and modeling X-43A electromechanical actuators[R]. NASA/TM 2008-214637.
[3] Cowan J R, Rae Ann Weir. Design and test of electro-mechanical actuators for thrust vector control[R]. N94-29650.
[4] John D Albright, Landon A Moore. Development and implementation of electromechanical actuators for the X-38 atmospheric test vehicles[R]. AIAA 2008-6569.
[5] Michael Garrison, Mark Davis, Scott Steffan. Human-rated upper stage thrust vector control system architecture selection[R]. AIAA 2007-5848.
[6] 朱忠惠,陈孟荦,胡隆庆,等. 推力矢量控制伺服系统[M]. 北京: 中国宇航出版社, 1995.
[7] 朱学平,祁鹏,张晓峰,等. 摆动喷管控制导弹鲁棒飞行控制系统设计[J]. 固体火箭技术, 2013, 36(4): 427-436.
[8] 陆豪,李运华,朱成林. 某型航天器推力矢量控制伺服机构的设计理论[J]. 北京航空航天大学学报, 2010, 36(12): 1417-1421.
[9] 夏长亮. 无刷直流电机控制系统[M]. 北京: 科学出版社, 2009.
(编辑:崔贤彬)
Design and modeling of a single nozzle-double pendulum electrical servo system
GAO Zhi-gang, ZHANG Jiao-long, ZHOU Jun, LI Peng
(Institute of Precision Guidance and Control, Northwestern Polytechnical University, Xi'an 710072,China)
To meet the miniaturization and high power requirement of swinging nozzle servo system for ATACMS, a system of single nozzle with double swing arm was developed based on Electromechanical Actuator(EMA). The nozzle was propelled by two vertical linear EMA consisting of brushless DC motor and ball screw reducer, which can realize the high power density and high efficiency, and then the large output torque and precise control can also be obtained. According to the kinematics analysis and modeling of the system, the kinematic nonlinear characteristic and cross-linked interference of the two linear EMA were researched, their formation reason, distribution regularities with swing angle and the effect to angle position were analyzed, and the computing method of dual channel command was obtained, which can realize the precise control to the direction and angle of swing nozzle by both EMA cooperation working.
swinging nozzle;electromechanical actuator;ball screw;brushless DC motor;kinematic nonlinear characteristic;cross-linked interference
2015-07-17;
:2015-09-07。
高智刚(1982—),男,讲师,从事高性能电动伺服系统设计与测试研究。E-mail:gaozhigang@nwpu.edu.cn
V421.6
A
1006-2793(2015)06-0888-05
10.7673/j.issn.1006-2793.2015.06.026
