关于一元函数可微条件讨论

张远平

（宁夏亘元房地产，宁夏 银川750021）

微分和导数是微积分中重要的两个概念，两者之间有着极为密切的关系，然而，高等数学教材中一元函数的可微性和可导性是等价的[1]，本文通过两道例题讨论了一元函数f（x）在x0处可微与>存在情况，由此给出一元函数在一点处可微的一个特殊结论。

例1[2]设函数f（x）在x=0连续，并且，求证：f′（0）存在，并且f′（0）=A.

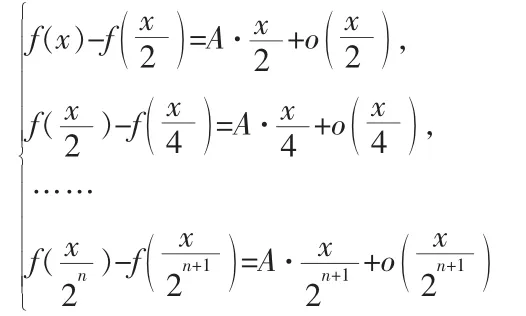
把上式加起来得：

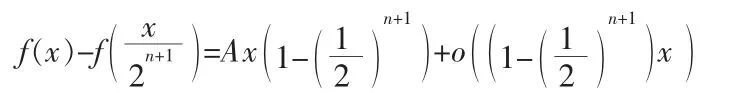
由于f（x）在x=0连续，上式两边对n→+∞取极限，得：

例2 函数f（x）=|x|，令x0=0,α=1,β=-1.

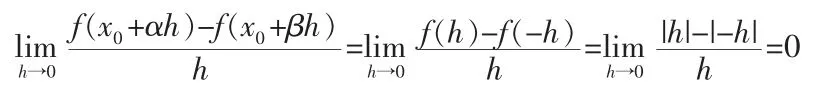
存在.但f（x）=|x|在x=0处不可微.

定理2 设f（x）在（x0-δ，x0+δ）（δ＞0）内有定义，且f（x）在x0连续，若

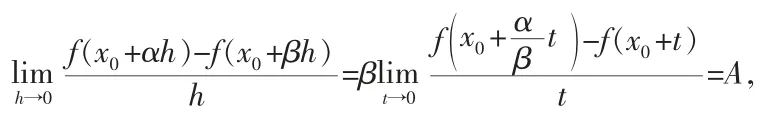
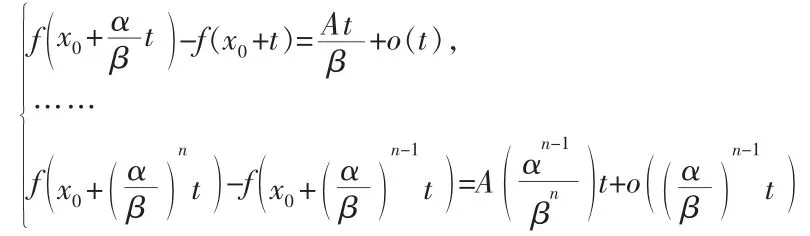
把上式加起来得：

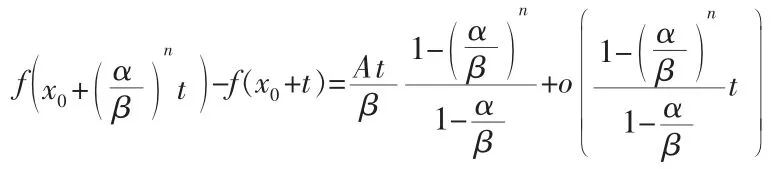
由于f（x）在x0连续，上式对n→+∞取极限得：

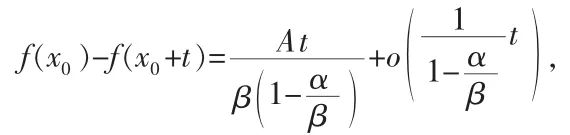
所以

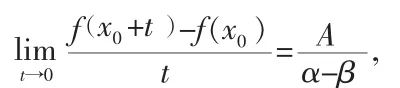
由定理1可得，f（x）在x0可微.同理可证，当|α|＞|β|时，f（x）在x0可微.所以，当|α|≠|β|时，f（x）在x0可微.

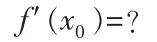
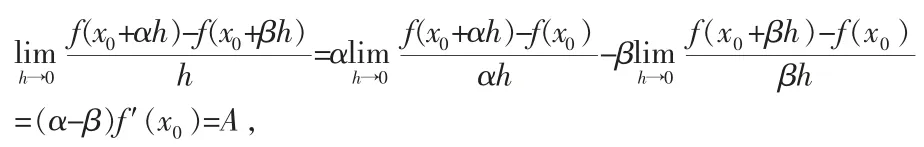
［1］刘士强.数学分析(上册)[M].南宁:广西民族出版社,2000,6:106-107.

［2］钱吉林,等.数学分析题解精粹[M].武汉:崇文书局,2003:163.