Coherence-based performance analysis of the generalized orthogonal matching pursuit algorithm

ZHAO Juan(赵娟), BI Shi-he(毕诗合) BAI Xia(白霞)TANG Heng-ying(唐恒滢) WANG Hao(王豪)

(1.School of Information and Electronics, Beijing Institute of Technology, Beijing 100081, China;2.Beijing Key Laboratory of Fractional Signals and Systems, Beijing 100081, China)



Coherence-based performance analysis of the generalized orthogonal matching pursuit algorithm

ZHAO Juan(赵娟), BI Shi-he(毕诗合)1,2, BAI Xia(白霞)1,2,TANG Heng-ying(唐恒滢)1,2, WANG Hao(王豪)1,2

(1.School of Information and Electronics, Beijing Institute of Technology, Beijing 100081, China;2.Beijing Key Laboratory of Fractional Signals and Systems, Beijing 100081, China)

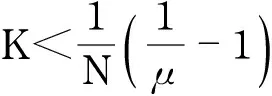
compressedsensing;sparsesignalreconstruction;orthogonalmatchingpursuit(OMP);supportrecovery;coherence

Among the existing recovery algorithms, two major approaches arel1-minimization and greedy algorithms.l1-minimization methods, such as basis pursuit (BP)[4], can work correctly for sparse signals by solving a convexl1minimization problem instead of thel0minimization, but require high computational complexity. On the other hand, greedy methods, such as orthogonal matching pursuit (OMP)[5], have received considerable attention due to their lower computational complexity and competitive performance. Greedy methods identify the supports of the sparse signal iteratively and construct an approximation on the estimated support until a halting condition is met. The OMP is the classical greed algorithm, which selects one column ofΦthat is most correlated with the current residual at each iteration. Some papers discussed the OMP performance of recovering sparse signals based on restricted isometry property (RIP)[6-7]and mutual incoherence property (MIP)[5,8-9]. Most of greedy algorithms such as regularized OMP (ROMP)[10], stagewise OMP (StOMP)[11], compressive sampling matching pursuit (CoSaMP)[12]and subspace pursuit (SP)[13]can be regarded as modifications of the OMP, mainly on the identification step, to improve the computational efficiency and recovery performance.

Recently, an extension of the OMP termed as generalized OMP (gOMP) has been proposed[14], which identifies multiple indices in each iteration by choosing indices corresponding toN(≥1) largest correlation in magnitude and can reconstruct sparse signals with much smaller number of iterations when compared to the OMP. The sufficient condition for perfectly recovering sparse signals via the gOMP has been derived based on RIP[14-15]. However, the performance of the gOMP in the framework of coherence has not been presented before. The goal of this paper is to provide the performance guarantees of the gOMP in terms of coherence to ensure identification of correct indices of sparse signals in noiseless and noisy cases. The achieved results can be regarded as extensions of the results of the OMP[5,8-9].

1 Generalized OMP algorithm

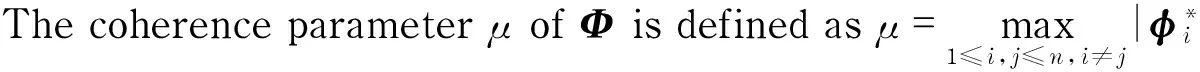
The generalized OMP identifies multiple indices in each iteration by choosing indices corresponding toN(≥1) largest correlation in magnitude[14]and its detailed description is shown in algorithm 1.

Algorithm1GeneralizedOMPalgorithm

Input：measurementsignaly∈Rm, measurement matrixΦ∈Rm×n, number of indices for each iterationN, halting threshold σ,maximumiterationskmax

Initialization：residualr0=y, estimated support setΛ0=∅, iteration counterk=1

Loop: atkth(k≥1) iteration

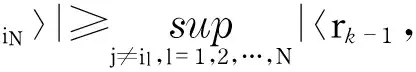
②Update estimated support set:Λk=Λk-1∪{i1,i2,…,iN}

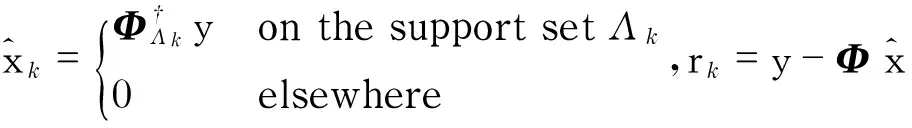
④If (‖rk‖2<δork≥kmax) break; else setk=k+1 and go to step 1)

End loop

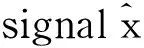
Case1IfT⊄Λk, we have

(1)

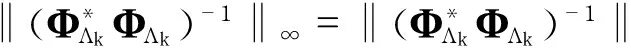
(2)

Thus

(3)

Case 2 IfT⊂Λk,wehave

(4)

FromEq.(4),weknowthataslongasatleastonecorrectindexisselectedineachiterationofthegOMP,T⊂ΛkwillholdafterKiterationsandthusthesparsesignalcanbeperfectlyrecovered.Successmeansthatatleastonecorrectindexischosenintheiteration.Inthenextsectionwewillanalyzecoherence-basedconditionguaranteeingthesuccessofthegOMPinnoiselessandnoisycases.

2 Coherence-based analysis of the generalized OMP algorithm

2.1 In noiseless case

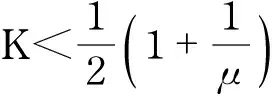
Theorem1Supposethaty=Φx, where x is aK-sparse vector with supportTandΦhas coherence parameterμ. The gOMP withN≥2 will perfectly recover anyK-sparse signal x within at mostKiterations if

(5)

Proof Mathematical induction method is used to prove the theorem. Suppose that the gOMP performedk-1 iterations successfully, i.e., Λk-1containsatleastk-1correctindices,thattosay, |Λk-1∩T|≥k-1and|Λk-1|=N(k-1),whichholdstruewhenk=1naturally.Letβ1denotesthelargestcorrelationinmagnitudebetweenrk-1andcolumnswhoseindicesbelongtoTΛk-1(i.e.,thesetofremainingcorrectindices)andαNdenotestheN-thlargestcorrelationinmagnitudebetweenrk-1andcolumnsindexedbyF={1,2,…,n}(T∪Λk-1)(i.e.,thesetofremainingincorrectindices).Forthekthiteration,toguaranteeselectingatleastonecorrectindex,werequire

β1>αN

(6)

Sincey=Φx,theresidualrk-1canbewrittenas

(7)

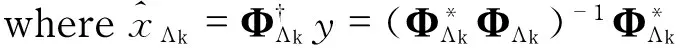
‖xTΛk-1‖∞-(|TΛk-1|-1)μ‖xTΛk-1‖∞-

(8)

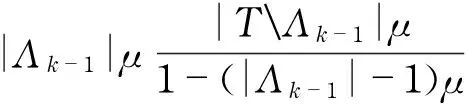
|TΛk-1|μ‖xTΛk-1‖∞

(9)

According to Eq.(8) and Eq.(9), we obtain the sufficient condition of Eq.(6) as

which can be simplified as

(10)

Since|TΛk-1|≤K-(k-1),toguaranteeEq.(10)holds,werequire

(11)

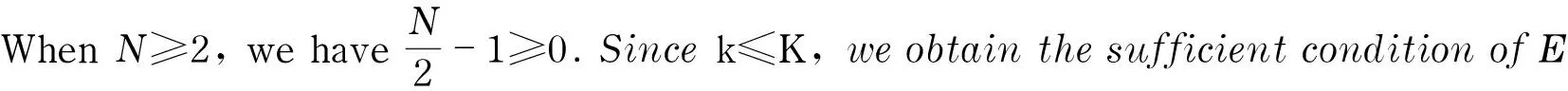
whichcanbereducedtoEq.(5).ThuswecanobtainthatEq.(6)willholdundertheconditiongivenbyEq.(5),whichguaranteesthatatleastonecorrectindexischoseninthekth iteration. That is to say,T⊆ΛKwillholdafteratmostKiterationsandthusthesparsesignalcanbeperfectlyrecovered.Theorem1isproved.

FromTheorem1wecanfindthatthesufficientconditionguaranteeingthatthegOMPwithN=2perfectlyrecoversanyK-sparsesignalisthesameasthatoftheOMP[5].

2.2Innoisycase

Inpracticalapplications,themeasurementsignalyisoftencontaminatedbynoise,i.e.,y=Φx+e,whereedenotestheboundednoisewith‖e‖2≤εorGaussiannoisewithe～N(0,σ2Im×m),whereIm×misidentitymatrix.

Theorem2 (boundednoisecase)Supposethatthenoisymeasurementsignaly satisfies y=Φx+e, where e denotes the noise with ‖e‖2≤ε, x be aK-sparse vector with supportTandΦhas coherence parameterμ. The gOMP withN≥2 will identify the support setTof anyK-sparse signal x within at mostKiterations if

(12)

Proof We still use mathematical induction method to derive the condition under which the identification step of the gOMP will select at least one correct index in each iteration.

Suppose that the gOMP performedk-1 iterations successfully, i.e., Λk-1containsatleastk-1correctindices,thattosay, |Λk-1∩T|≥k-1and|Λk-1|=N(k-1),whichholdstruewhenk=1naturally.Atthekthiteration，toguaranteechoosingatleastonecorrectindex,westillrequirethatEq.(6)holds.

Accordingtoy=Φx+e,theresidualrk-1canbewrittenas

(13)

In addition, note that ‖e‖2≤εandusingEq.(2),wehave

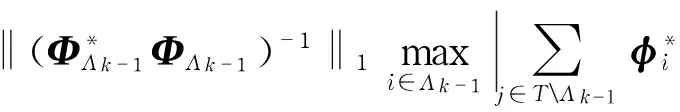
(14)

Using Eq.(13) and Eq.(14), we have

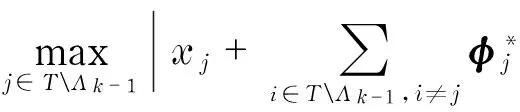
‖xTΛk-1‖∞-(|TΛk-1|-1)μ‖xTΛk-1‖∞-

(15)

Ontheotherhand,wecanobtain

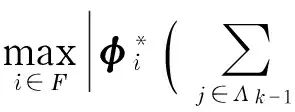
|TΛk-1|μ‖xTΛk-1‖∞+ε

(16)

Combing Eq.(15) and Eq.(16), to guarantee Eq.(6) holds, we require

‖xTΛk-1‖∞-(|TΛk-1|-1)μ‖xTΛk-1‖∞-

|TΛk-1|μ‖xTΛk-1‖∞+ε

which can be reduced to

Since ‖xTΛk-1‖∞≥xminand|TΛk-1|≤K-(k-1),weobtainthesufficientconditionofEq.(6)as

(17)

whichcanbereducedtoEq.(12).ThuswecanobtainthatEq.(6)willholdundertheconditiongivenbyEq.(12),whichguaranteesthatatleastonecorrectindexischoseninthekth iteration. That is to say,T⊆ΛKwillholdafteratmostKiterations.Theorem2isproved.

FurthermoreweconsiderthecaseofGaussiannoise.Ife～N(0,σ2Im×m),itisshownthat[9]

(18)

ByusingEq.(18)togetherwithTheorem2,wecandirectlyobtainthefollowingresult.

Theorem 3 (Gaussian noise case) Suppose that the noisy measurement signalysatisfiesy=Φx+e,wheree～N(0,σ2Im×m),xbeaK-sparsevectorwithsupportTandΦhascoherenceparameterμ.If

(19)

thenthegOMPwithN≥2 will identify the support setTofxwithinatmostKiterationswithprobabilityatleast1-1/m.

Similarly,fromTheorem2andTheorem3itisshownthatthesufficientconditionsguaranteeingthatthegOMPwithN=2identifiesthecorrectsupportofanyK-sparsesignalarethesameasthoseoftheOMP[8-9].

3 Conclusion

Inthispaper,theperformanceofthegOMPalgorithmwhichidentifiesmultipleindicesperiterationtoreconstructsparsesignalswithmuchsmallernumberofiterationsisanalyzedintermsofcoherence.SomesufficientconditionsensuringidentificationofthesupportofsparsesignalsviathegOMParederivedinthenoiselessandnoisycases.Theachievedresultsmaybenefittheunderstandingandanalysisofgreedyalgorithms.

[1] Donoho D L. Compressed sensing [J]. IEEE Transactions on Information Theory, 2006, 52(4): 1289-1306.

[2] Candes E J, Romberg J, Tao T. Robust uncertainty principles: exact signal reconstruction from highly incomplete frequency information [J]. IEEE Transactions on Information Theory, 2006, 52(2): 489-509.

[3] Tsaig Y, Donoho D L. Extensions of compressed sensing [J]. Signal Processing, 2006,86(3):549-571.

[4] Kim S, Koh K, Lustig M, et al. An interior-point method for large scale L1 regularized least squares [J]. IEEE Journal of Selected Topics in Signal Processing, 2007, 1(4):606-617.

[5] Tropp J A. Greed is good: algorithmic results for sparse approximation [J]. IEEE Transactions on Information Theory, 2004,50(10):2231-2242.

[6] Zhang Tong. Sparse recovery with orthogonal matching pursuit under RIP [J]. IEEE Transactions on Information Theory, 2011,57(9):6215-6221.

[7] Wu Rui, Huang Wei, Chen Di Rong. The exact support recovery of sparse signals with noise via orthogonal matching pursuit [J]. IEEE Signal Processing Letters, 2013,20(4):403-406.

[8] Donoho D L, Elad M, Temlyakov V N. Stable recovery of sparse overcomplete representations in the presence of noise [J]. IEEE Transactions on Information Theory, 2006,52(1):6-18.

[9] Cai T T, Wang Lie. Orthogonal matching pursuit for sparse signal recovery with noise [J]. IEEE Transactions on Information Theory, 2011,57(7):4680-4688.

[10] Needell D, Vershynin R. Signal recovery from incomplete and inaccurate measurements via regularized orthogonal matching pursuit [J]. IEEE Journal of Selected Topics in Signal Processing, 2010, 4(2):310-316.

[11] Donoho D L, Tsaig Y, Drori I, et al. Sparse solution of underdetermined systems of linear equations by stagewise orthogonal matching pursuit[J]. IEEE Transactions on Information Theory, 2012, 58(2): 1094-1121.

[12] Needell D, Tropp J A. Cosamp: Iterative signal recovery from incomplete and inaccurate samples [J]. Applied and Computational Harmonic Analysis, 2009, 26(3):301-321.

[13] Dai Wei, Milenkovic O. Subspace pursuit for compressive sensing signal reconstruction [J]. IEEE Transactions on Information Theory, 2009,55(5):2230-2249.

[14] Wang Jian, Kwon S, Shim B. Generalzied orthoginal matching pursuit [J]. IEEE Transactions on Signal Processing, 2012, 60(12):6202-6216.

[15] Satpathi S, Das R, Chakraborty M. Improving the bound on the RIP constant in generalized orthogonal matching pursuit[J]. IEEE Signal Processing Letters, 2013, 20(11): 1074-1077.

[16] Elad M. Sparse and redundant representations: from theory to applications in signal and imaging processing [M]. New York: Springer, 2009.

(Edited by Cai Jianying)

10.15918/j.jbit1004-0579.201524.0313

TN911.7Documentcode:AArticleID: 1004- 0579(2015)03- 0369- 06

Received2014- 01- 04

SupportedbytheNationalNaturalScienceFoundationofChina(60119944,61331021);theNationalKeyBasicResearchProgramFoundedbyMOST(2010CB731902);theProgramforChangjiangScholarsandInnovativeResearchTeaminUniversity(IRT1005);BeijingHigherEducationYoungEliteTeacherProject(YETP1159)

E-mail: juanzhao@bit.edu.cn