基于模拟退火算法的卡尔曼滤波在室内定位中的应用研究

殷守林, 刘天华, 李 航

(沈阳师范大学 科信软件学院, 沈阳 110034)



基于模拟退火算法的卡尔曼滤波在室内定位中的应用研究

殷守林, 刘天华, 李 航

(沈阳师范大学 科信软件学院, 沈阳 110034)

卡尔曼滤波算法是用来解决定位中滤波的问题的一个重要内容,但由于预测和测量值之间的误差比较大,算法并没有达到最优,因为在室内定位中温湿度(高斯白噪声)对其有影响,以及非平面中的位置信息影响人员物品的位置定位精确度。针对卡尔曼滤波算法的这一问题,引进模拟退火算法。结合模拟退火算法的降温思想,采用迭代选取最优解,以此为基础,得到的最优解用于卡尔曼的初始值;将得到的最优距离作为对象,并以此建立邻域,最后再用线性插值法得到坐标。仿真实验表明,此种方法有效提高了室内定位精确度,减小降低了各种因素的干扰。

模拟退火算法; 卡尔曼滤波算法; 室内定位; 线性插值

0 引 言

定位实现过程中必须考虑的重要因素就是噪声干扰。针对室内定位中提出的一些滤波算法具有代表性的就是Rudolf Emil Kalman在他的博士论文中提出的卡尔曼滤波算法[1],把含噪声的数据进行处理之后得出相对真值,卡尔曼算法是以均方差为估计采用递推估计理论的算法,由测量值来更正系统状态向量,以“预测-实测-修正”的顺序递推。根据测量值来消除随机干扰,出现新的系统状态。关于定位的研究也有很多文章[6],但大部分以空间模型为基础。而卡尔曼滤波采用信号与噪声的状态空间模型,它利用前一时刻的估计值和现在时刻的观测值来更新对状态变量的估计,求出现时刻的估计值。卡尔曼滤波有效的解决了在定位过程中出现的噪声影响,大大提高了定位的精确度[2-6]。但是卡尔曼滤波算法的初始值选取比较困难,因此又出现了一些改进的卡尔曼滤波[7-13],然而大部分都是在过程中进行优化。

模拟退火算法最早是由N.Metropolis等人于1953年提出的,是基于Monte-Carlo迭代求解策略的一种随机寻优的算法。模拟退火算法的基本思想是从某一较高对出事温度出发,伴随着温度参数的不断下降,结合概率突跳特性在解空间中随机寻找目标函数的全局最优解,即在局部最优解能概率性地跳出并最终趋于全局最优。模拟退火算法是一种通用的优化算法[14-15],理论上算法具有概率的全局优化性能。因此卡尔曼滤波需要一个优质的初始解,那么模拟退火算法得到的最优解可以作为卡尔曼滤波的初始解。这种思想鲜有人提出,因此本文提出在室内定位中的卡尔曼滤波,该滤波算法引进模拟退火算法思想,避免高斯白噪声影响数据采集的误差偏大。由于在室内无线网络读取的信号强度样本比较小,目标移动曲线受到客观因素影响导致不平缓,使系统的稳定性和准确性受到严重影响。针对这一出现的问题,在深入理解基于卡尔曼滤波的室内无线定位原理的基础上,本文引入一种模拟退火卡尔曼滤波算法来对估算出的目标位置信息进行滤波处理,再通过线性插值法进行误差补偿,最后通过仿真验证了该方法确定可行并提高了定位的精度。

1 基于模拟退火的卡尔曼滤波算法

在室内定位中使用卡尔曼滤波进行滤波处理,并提高定位精度,同时引进模拟退火算法寻找优化的初始解,跳出局部最优解而搜索到全局最优解。模拟退火算法的具体实施步骤如下:

第1步 数据初始化,初始温度T(充分大),初始状态S(算法迭代起点),每个T值的迭代次数L。

第2步 对K=1,2,3,…,L做第3步至第6步。

第3步 产生新解S′。

第6步 如果满足终止条件则输出当前解作为最优解,结束程序。终止条件通常取为连续若干个新解都没有被接受时终止算法。

第7步T逐渐减少,且T→0,然后转第2步。

模拟退火算法的基本思想分为3个部分:解空间、目标函数、初始解部分。模拟退火算法由一个目标函数产生一个位于空间的新解,计算新解与初始解的目标函数差,使用接受准则判断新解是否符合当前条件,进行迭代运算。最大的优点就是与初始值无关。卡尔曼滤波就是用来求得估计值的最佳解,通过引进模拟退火算法,二者有效结合,能最终达到进一步提高定位的精确度。

1.1 信号强度的初始化

信号强度的采样:设Eij表示第i个采样点接收到第j个AP的信号强度的平均值,在各个采样点处测量。实时定位设Gj表示接收到来自第j个AP信号强度的平均值,具体的定位计算公式由明考斯基距离公式得:

当q=1,dij表示曼哈顿距离。

当q=2,dij表示欧式距离。由实验结果表明,当q=2时,系统的定位精度比较高。得到:

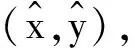
1.2 模拟退火算法的室内定位流程图

从图1中可以得出,首先要确定一个初始信号强度,根据欧氏距离公式进行计算,得到di的值,同时可以看出在精确未知点位置的时候,是以信号强度来定的,而信号强度的精确度是以具体的公式计算

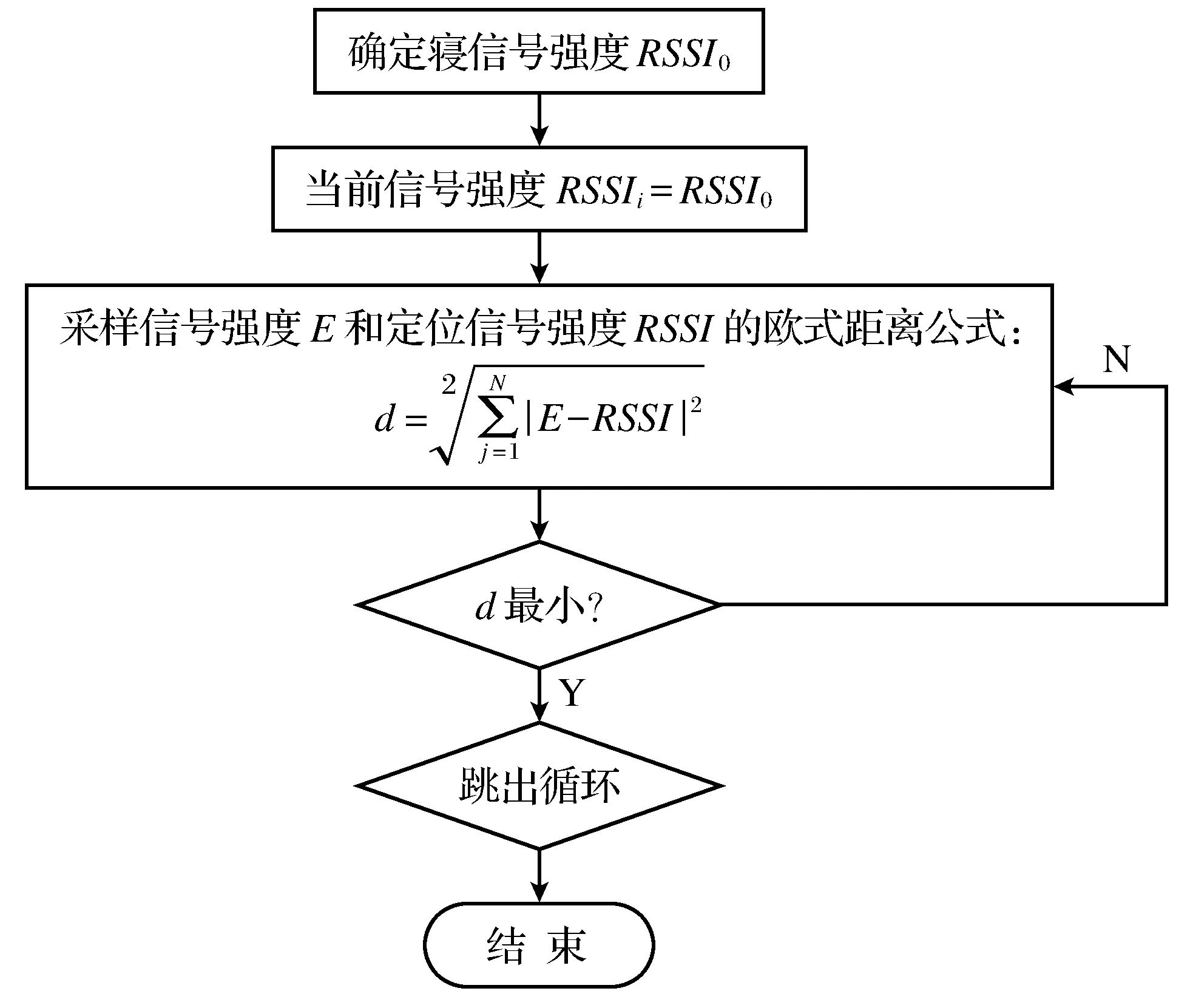
图1 模拟退火算法流程图

得到。

1.3 滤波函数的设置

信号强度接收器接收的信号强度,可以直接测量出来。经过多次测量,可以得到一个估计的强度,假如预测第k-1次的信号强度是RSSIk-1,那么在k时刻信号强度与k-1时刻的预测值相等,即RSSIk=RSSIk-1,同时该值的高斯白噪声为ε0:

其中:RSSIMoptimal表示k-1时刻的最优信号值偏差;RSSIforcast表示k时刻自己对信号强度的预测不确定值偏差。通过测量仪得到k时刻信号强度是RSSImeasure,同时该值的偏差是ε1:

其中:RSSIMoptimal表示测量值的最优信号强度偏差;RSSIMforcast表示测量的不确定值偏差。

由此,得到均方误差Herror,其表达式为:

因此估算出K时刻最优信号强度RSSIKoptimal值为:

RSSIKoptimal=RSSIk-1+Herror×(RSSImeasure-RSSIk-1)

从而,卡尔曼滤波不断地把均方误差递归,能够得到最优的信号强度值,运行速度快,且只保留上一时刻的方差。

1.4 模拟退火算法思想的具体实施

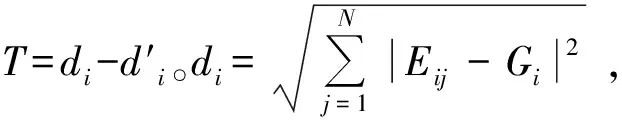
1.5 线性插值法

线性插值是数学、计算机图形学等领域广泛使用的一种简单插值方法[16],如图2所示。假设已知坐标(x1,y1)和(x2,y2),要得到[x1,y2]区间内某一位置x在直线上的y值。

图2 线性插值法

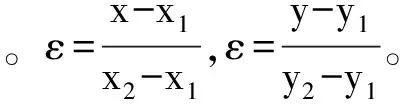
2 仿真及结果分析

在MATLAB仿真平台下进行的仿真验证,通过在信号发射点半径不变的圆上,布置不同的点,测量接收到的信号强度计算出的距离值的误差大小来判断哪个方法更优,将未加入模拟退火的卡尔曼作为对比对象,2个算法仿真是在相同的参量,同一背景环境下进行,仿真结果如图3、图4所示。

由图3可以看出在10～100 s,卡尔曼滤波算法比其上下波动大,模拟退火卡尔曼优势很明显,定位比其更加准确。经计算100 s之后,曲线也逐渐收敛,曲线走势趋于平稳,滤波达到一种稳定状态。图4表明这种算法的结合误差变化会越来越稳定,上下波动会越来越小,有效提高定位精确度。

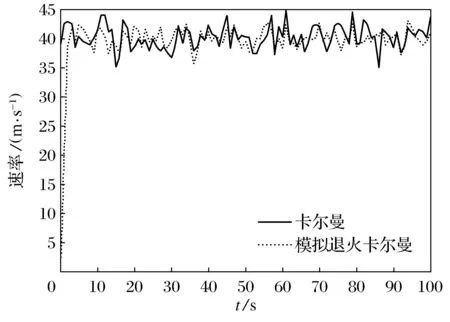
图3 卡尔曼与模拟退火卡尔曼的定位比较

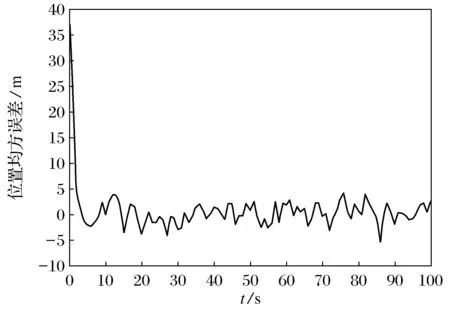
图4 模拟退火卡尔曼的误差变化

从图3和图4可以看出模拟退火卡尔曼的整体高效性。经过分析比较可以得到如下结论:

1) 使用模拟退火卡尔曼滤波算法,随着时间的增加,该算法越来越收敛,误差波动越来越小。

2) 在室内定位中,单纯的卡尔曼滤波可以完成此项工作,但是误差较大,结合模拟退火算法之后,很明显误差波动范围小,使定位趋于精确化。

3) 在室内定位初值选取时候,各个点的坐标初始位置直接精确化,对于后期目标运动轨迹位置确定有很大帮助,大大提高精确度。

3 结 论

本文提出的策略是模拟退火算法和卡尔曼滤波算法有效结合,在卡尔曼算法的基础上引入模拟退火算法求解初始解,增加初始值的准确性,降低了噪声干扰,有效的解决了在定位系统中定位精确度受其他客观因素影响地问题,仿真实验结果表明,该策略能够能够在室内定位中更有效的提高精确度。部分实验数据具体见表1。

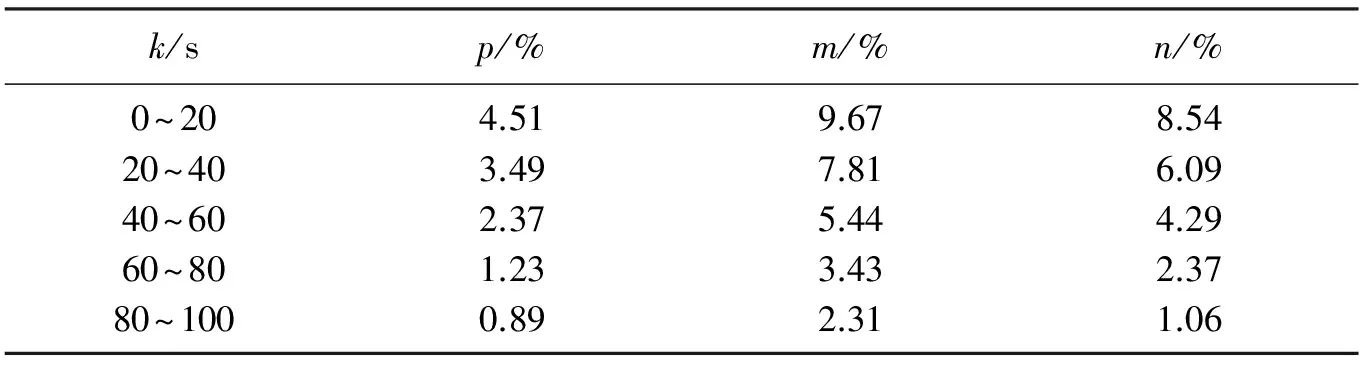
表1 实验数据测量值

注:k为时间段;p为随时间变化模拟退火卡尔曼滤波位置误差;m为随时间变化卡尔曼算法的误差;n为随时间变化模拟退火卡尔曼滤波误差。

在本文中选取50个点,进行了50次实验。采样周期T=20 s,通过卡尔曼滤波方程以及新方法计算求得p、m、n。

[1]KALMAN R E.A new approach to linear filtering and prediction problems[J].J Fluids Eng, 1960,82(1):35-45.

[2]曹春萍,罗玲莉.基于卡尔曼滤波算法的室内无线定位系统[J].计算机系统应用, 2011(11):76-79.

[3]赵永翔,周怀北,陈淼,等.卡尔曼滤波在室内定位系统实时跟踪中的应用[J].武汉大学学报:理学版, 2009,55(6):696-700.

[4]付梦印,邓志宏,闫莉萍.Kalman滤波理论及其在导航系统中的应用[M].北京:科学出版社, 2010.

[5]顾宗海.基于RSSI测距的室内定位算法研究[D].郑州:郑州大学, 2011.

[6]陈豫章.基于RSSI的室内三维定位技术研究与实现[D].昆明:云南大学, 2013.

[7]张明华,张申生,曹健.无线局域网中基于信号强度的室内定位[J].计算机科学, 2007(6):68-75.

[8]ZHANG D F, JIANG X P, HU Z C, et al.Rolling and annealing texture of 3004 aluminium alloy[C]∥Materials science forum, 2002,408:1477-1482.

[9]SHIEH L S, WAI W B, YATES R E.Approximate Kalman filters[C]∥Joint Automatic Control Conference, San Francisco, CA, 1980.

[10]CHUI C K, CHEN G.Kalman filtering[J].With real time applications, 1999.

[11]BISHOP G, WELCH G.An introduction to the kalman filter[J].Proc of SIGGRAPH, Course, 2001,8(27599-23175):41.

[12]CHRISTOFFERSEN P, DORION C, JACOBS K.Nonlinear Kalman filtering in affine term structure models[J].Management Science, 2012:2012-2014.

[13]SARKKA S, HARTIKAINEN J.Non-linear noise adaptive Kalman filtering via variational Bayes[C]∥Machine Learning for Signal Processing (MLSP), 2013 IEEE International Workshop on.IEEE, 2013:1-6.

[14]HAMZEEI M, FARAHANI R Z, RASHIDI-BEJGAN H.An exact and a simulated annealing algorithm for simultaneously determining flow path and the location of P/D stations in bidirectional path[J].J M anufsyst, 2013,32(4):648-654.

[15]INGBER L.Simulated annealing: Practice versus theory[J].Math Comput Mode, 1993,18(11):29-57.

[16]李培明,梅胜全,马青坡.一种改进的双线性插值射线追踪方法[J].石油地球物理勘探, 2013(4):553-558.

[17]BROWN A, RUSCHMANN M, DUFFY B .Simulated Annealing Maneuver Planner for Cluster Flight[C]∥24 th International Symposium on Space Flight Dynamics, Laurel, 2014.

[18]赵煌,彭勇.双线性插值算法的优化及其应用[J].电视技术, 2012,36(17):30-32.

Application of Kalman filtering in indoor location based on simulated annealing algorithm

YINShoulin,LIUTianhua,LIHang

(Software College, Shenyang Normal University, Shenyang 110034, China)

Kalman filtering algorithm is used to solve the problem of the positioning filter, however the error is relatively large between the measured value and predicted value.The algorithm does not reach the optimal solution because there exists temperature and humidity (we can call it Gaussian white noise) as well as the location information of non-planar affects positioning accuracy of human’s site in the indoor location.We introduce the simulated annealing algorithm to the significant difference of Kalman filtering algorithm.We combine the cooling of simulated annealing algorithm and use the iterative to select the optimum solution.On this basis, we can get the optimal solution for initial value of the Kalman.Getting the optimal as an object and we set up neighborhood based on the object.At the end we can get coordinate by linear interpolation method.Simulation experiments show that this method can improve effectively the positioning accuracy and reduce the interference of various kinds of factors.

simulated annealing algorithm; Kalman filtering algorithm; indoor localization; linear interpolation

2014-10-06。

国家自然科学基金资助项目(60970112)。

殷守林(1990-),男,河南濮阳人,沈阳师范大学硕士研究生; 刘天华(1966-),男,辽宁沈阳人,沈阳师范大学教授,博士,硕士研究生导师。

1673-5862(2015)01-0086-05

TP391.9

A

10.3969/ j.issn.1673-5862.2015.01.019