五维系统的混沌动力学分析

王 鹍, 刘亚秋, 郝 兵, 史庆武

(1.佳木斯大学 信息电子技术学院, 黑龙江 佳木斯 154007;2.东北林业大学 信息与计算机工程学院, 哈尔滨 150040)



五维系统的混沌动力学分析

王 鹍1,2, 刘亚秋2, 郝 兵1, 史庆武1

(1.佳木斯大学 信息电子技术学院, 黑龙江 佳木斯 154007;2.东北林业大学 信息与计算机工程学院, 哈尔滨 150040)

以一个五维混沌系统为研究对象,利用状态变量反馈方法,引入一个线性控制器,形成一个五维受控系统。利用李雅普诺夫方法和劳斯稳定判据进行理论分析,设计控制器,求出受控系统渐近稳定的控制律。采用数值仿真试验的方法进一步研究该五维受控系统的动力学行为及其混沌运动特征。线性控制器在不同的参数区域内选取控制参数,该五维受控系统的响应曲线呈现出平衡点渐近稳定、收敛到某些固定点、周期轨道运动、新混沌的分岔现象。提供了一个动力学性态丰富的五维混沌控制和反控制系统。对需求高维混沌信号的混沌保密通信等相关领域提供了理论和试验支持。

五维混沌系统; 动力学分析; 混沌控制

0 引 言

随着网络信息技术和通信技术的快速发展,通信的安全性和保密性危机日趋严重。由于混沌信号自身对初始条件十分敏感,具有非周期、连续宽频带、似噪声的复杂随机特性,经过混沌信号调制后的信号即使被敌方截获,也很难被破译,因此,混沌同步的理论和技术被重点应用在混沌保密通信等相关领域[1-2],这就急需研究发现复杂的混沌系统作为信号源。

混沌现象多种多样,混沌系统亦多种多样。当混沌现象有害时,设法抑制混沌,当混沌有益时,善加利用,这就是混沌控制和反控制。较成熟的混沌系统研究主要集中在一些低维的混沌系统上,如Logistic映射[3]、气象学中的Lorenz系统[4],陈氏系统[5]、吕氏系统[6]、电路中的Chua系统等[7]。而高维混沌系统,由于其动力学行为复杂,运动模型往往未知,高维系统混沌的研究刚刚起步[8-10]。

一般来讲,混沌系统维数越高,系统响应越复杂,倘若选择高维的混沌系统、超混沌系统作为混沌源信号,对原始信号进行掩盖加密,信息传递的安全性将会更高。目前存在的问题是模型结构已知的高维混沌系统并不多,虽有几种五维系统正在信号加密的探索中[11-13],但是其动力学行为并不丰富,远不能满足实际的需要。因此,发现更多的高维混沌系统及研究其动力学行为迫在眉睫。

本文以五维系统作为研究对象,引入状态变量反馈,使用解析法和仿真实验来分析五维受控系统的非线性动力学行为,发现系统出现了分岔现象[14-15],具有混沌及周期等多种运动状态。

1 五维系统混沌模型及仿真

所选的一类五维非线性系统的微分方程为:

在文献[16]中,取a=3.9,b=9.17,c=3.94,d=7.068,e=1时,该五维系统数学模型为:

计算求得系统(2)的2个平衡点,分别是[1,0,0,0,0]T和[-1,0,0,0,0]T。

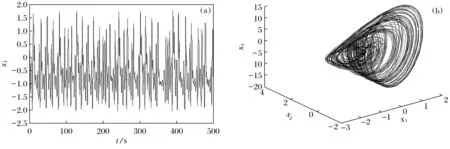
(a)—状态变量x1的响应; (b)—系统的三维相图(x1,x2,x5)。

该五维系统的相轨迹是不规则的杂乱波,始终在一个有界的区域里,图1b出现了奇怪吸引子现象,满足混沌特征。因此,该五维系统是混沌系统,从整体上说混沌是稳定的,但平衡状态不稳定。

2 平衡状态渐近稳定

2.1 控制器的设计

为了实现五维系统的相轨迹渐近收敛到平衡状态,将一个或几个变量反馈引入系统,根据反馈控制原理设计控制器,求取控制规律。

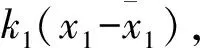
根据李雅普诺夫方法求得系统(3)平衡状态的雅可比矩阵:

线性化后得到特征方程为:

利用劳斯稳定判据,计算求得控制律:当相轨迹渐近收敛到平衡点[1,0,0,0,0]T时,反馈k1取值区域为k1>1;当相轨迹渐近收敛到平衡点[-1,0,0,0,0]T时,反馈的取值区域为k1>2。

2.2 数值仿真实验

在k1>2的广大区域内选取参数做仿真实验,取k1=15,数值仿真如下。

1) 受控系统的相轨迹收敛到第1个平衡点,仿真如图2所示。

(a)—x1的相图; (b)—受控系统的三维相图(x1,x2,x5)。

2) 受控系统的相轨迹收敛到第2个平衡点,仿真如图3所示。

(a)—x1的相图; (b)—三维相图(x1,x2,x4)。

理论分析知道,当k1>2时,2个平衡状态都能渐近稳定,仿真实验验证了理论的正确性。

3 实验分析受控系统其他运动状态

3.1 受控系统周期运动

(a)—x1的响应图; (b)—二维相图(x2,x3)。

3.2 受控系统状态轨迹收敛

(a)—x1的响应图; (b)—x2的响应图; (c)—二维相图(x4,x5); (d)—三维相图(x1,x3,x4)。

从图5可知,反馈参数k1=0.62时,五维受控系统收敛到点[0.42,-0.36,0,0,0]T。

3.3 系统出现新的混沌

当k1=0时,受控系统是原系统(2),混沌图形如图1所示。当k1<0时,大量仿真实验表明受控系统出现新的混沌。取k1=-2,仿真结果见图6。

(a)—x2的相图; (b)—系统的三维相图(x1,x3,x5)。

由图6、图4和图5可知,k1在不同的参数区域选值,受控系统出现由混沌到周期运动再到收敛的跳变,出现了分叉现象,动力学性态丰富。

4 结 语

本文将一个五维混沌系统引入一个状态变量反馈,利用李雅普诺夫方法和劳斯稳定判据求出受控系统渐近稳定的解析解。通过大量的仿真实验研究,确定出不同的参数区域,当选取不同的控制参数时,该五维受控系统呈现出平衡点稳定、收敛、周期运动等动力学行为,实现了五维系统的混沌控制和反控制,为混沌保密通信等相关领域需要的复杂混沌信号提供了理论和试验支持。

[1]PECORALM, CARROLLT L.Synchronization in chaotic systems[J].Phys Rev Lett, 1990,64(8):821-824.

[2]朱从旭,孙克辉.基于新型类洛伦兹吸引子的混沌同步保密通信系统[J].山东大学学报:理学版, 2011,46(9):5-11.

[3]MAY R M.Simple mathematical models with very complicated dynamics[J].Nature, 1976,261(10):459-474.

[4]LORENZ E N.Deterministic Non-periodic Flows[J].Atmos Sci, 1963,20:130-141.

[5]CHEN G, UETA T.Yet another chaotic attractor[J].Bifurcation and Chaos, 1999,9(7):1465-1466.

[6]LU J H, CHEN G.Dynamical analysis of a new chaotic attractor[J].Bi-furcat Chaos, 2002,12(5):1001-1015.

[7]CHUAL O, KOMURO M.The double scroll family partsⅠandⅡ[J].IEEE Transactions on Circuits and Systems.Part I, 1996,33:1073-1118.

[8]AUERBACH D, GREBOGI C, DTT E, et al.Controlling chaos in high dimensional systems[J].Phys Rev Lett, 1992,69(24):3479-3482.

[9]REYL C,FLEPP L.Control of NMR-laser chaos in high-dimensional embedding space[J].Phys Rev E, 1993,47(1):267-272.

[10]PRTRO V, MIHALIUL E.Stabilizing and characterizing unstable states in high-dimensional systems from time series[J].Phy Rev E, 1995,51(5):3988-3996.

[11]魏亚东,周爱军.一个新五维超混沌系统的动力学分析[J].舰船电子工程, 2012,32(7):68-70.

[12]韩峰,唐驾时.一个五维受控混沌系统的动力学行为[J].动力学与控制学报, 2010,8(3):250-252.

[13]ZHU Jianliang, ZHAO Hongchao.Five-dimensional chaotic system and its circuitry implementation[C]∥CISP, 2009:83-85.

[14]ALGABA A, GAMERO E.A degenerate Hopf-saddle-node bifurcation analysis in a family of electronic circuits[J].Nonlinear Dynamic, 2007,48:55-67.

[15]MAO Xiaochen.Stability and Hopf bifurcation analysis of a pair of three-neuron loops with time delays[J].Nonlinear Dynamics, 2012,68(1/2):151-159.

[16]CHLOVERAKIS K E, SPROTT J C.Chaotic hyper jerk systems[J].Chaos Solition Fract, 2006,28(3):739-746.

Analysis of chaotic dynamics of five-dimensional system

WANGKun1,2,LIUYaqiu2,HAOBing1,SHIQingwu1

(1.College of Information and Electronic Technology, Jiamusi University, Jiamusi 154007, China;2.College of Information and Computer Engineering, Northeast Forestry University, Harbin 150040, China)

A 5-dimensional chaos system is taken as the object of this paper.A linear controller is introduced by the state variables feedback method to form a 5-dimensional controlled system.The Lyapunov method and the Routh criterion are used for theoretical analysis and controller design, and then a control law of asymptotical stable controlled system is obtained.The dynamic behavior and its chaos motion characteristics of this 5-dimensional controlled system are further studied by the numerical simulation method.Given linear controller with the control parameters selected in different regions, the response curves of this 5-dimensional controlled system show the bifurcations such as asymptotic stability at the equilibrium point, convergence at some fixed points, periodic orbit motion, new chaos, etc.A rich characteristic dynamic 5-dimensional chaos control and anti-control system is proposed here, providing theoretcial and experimental support for the related fields of chaos secure communication, which require high-dimensional chaos signals.

five-dimensional chaotic system; dynamic analysis; chaos control

2014-10-26。

国家自然科学基金资助项目(31370565); 佳木斯大学面上科研项目(L2010-128); 黑龙江省自然科学基金资助项目(E201212); 黑龙江省教育厅科研面上项目(12521539)。

王 鹍(1975-),女,黑龙江佳木斯人,佳木斯大学讲师,东北林业大学博士研究生; 通信作者: 刘亚秋(1971-),男,辽宁法库人,东北林业大学教授,博士,博士研究生导师。

1673-5862(2015)01-0076-05

TP13

A

10.3969/ j.issn.1673-5862.2015.01.017