极小化加权总完工时间的可拒绝单机排序问题

闫力君, 赵玉芳

(沈阳师范大学 数学与系统科学学院, 沈阳 110034)



极小化加权总完工时间的可拒绝单机排序问题

闫力君, 赵玉芳

(沈阳师范大学 数学与系统科学学院, 沈阳 110034)

在经典的排序问题中,工件的加工时间是固定不变的。然而,在实际生产中,工件的实际加工时间会发生变化。同时,机器通常需要进行保养,或发生故障时进行维修等原因,导致机器在某一时间段内无法工作,即机器的不可用区间。研究带有到达时间、退化效应和拒绝工件,及机器带有不可用区间的单机排序问题。在这一模型中,工件的开始加工时间越晚,其实际加工时间越大,实际加工时间是与其开始加工时间有关的函数。该问题中工件允许被拒绝。如果工件被拒绝,那么需要支付拒绝惩罚。讨论的目标函数是接受工件的加权总完工时间与所有拒绝工件的拒绝惩罚之和。首先说明该问题是一般意义NP-难的,进而利用划分程序的方法给出了一个全多项式近似方案,最后分析了该近似方案的时间复杂性。

拒绝惩罚; 退化效应; 全多项式近似方案; 不可用区间

在经典的排序问题中,工件的实际加工时间是一个固定参数。但是,在实际生产中,工件的实际加工时间不一定是固定的。文献[1-4]研究了带有退化效应模型的单机排序问题,其中工件的实际加工时间与其开始加工时间有关。分别研究了最大完工时间、总完工时间、加权总完工时间等问题。文献[5-6]研究了工件允许被拒绝的排序问题,分别研究了最大完工时间、加权总完工时间问题。文献[7]研究了工件的实际加工时间与其开始加工时间有关的平行机排序问题,目标函数是总完工时间,利用划分程序的方法给出该问题的全多项式近似方案。文献[8-9]研究了工件加工时间带有退化效应的单机排序问题,证明了问题在多项式时间内可解。文献[10-11]研究了带有不可用区间的最大完工时间问题。文献[12]研究了目标函数为加权总完工时间的单机和平行机排序问题,并且机器带有不可用区间,说明了单机和平行机问题都是NP-难的,并且给出了启发式算法。文献[13]研究了2台机器的流水作业排序问题,证明了最大完工时间问题是NP-难的,并且给出了拟多项式时间的动态规划算法。文献[14-15] 研究了带有不可用区间的排序问题,分别对中断继续及中断重复的情形进行了研究。

同时带有拒绝惩罚及不可用区间的现象非常普遍,本文将上述问题结合起来,讨论了带有到达时间、退化效应、拒绝工件及机器带有不可用区间的单机排序问题,目标函数是接受工件的加权总完工时间与所有拒绝工件的拒绝惩罚之和。利用划分程序的方法给出了一个全多项式近似方案,并分析该近似方案的时间复杂性。

1 问题描述

具体问题描述如下:n个互不相关的工件J1,J2,…,Jn在一台机器上加工,所有工件具有相同的到达时间t0,且t0>0;工件Jj的实际加工时间为pj=bjt,其中bj>0为工件Jj的退化因子;t为其开始加工时间,显然t≥t0>0;ej>0是工件Jj被拒绝时的惩罚。记被加工的工件的集合为S,所有被拒绝的工件的集合为R。[T1,T2)为机器的不可用区间,在此区间内机器不能加工任何工件。nr-a表示机器为不可恢复的,即某个工件在不可用区间之前没加工完,则在不可用区间之后需要重新加工这个工件。目标函数是接受工件的加权总完工时间与所有拒绝工件的惩罚之和。同时具有到达时间、退化效应、拒绝工件及机器带有不可用区间的单机排序问题,利用三参数表示法α|β|γ可记为

2 全多项式近似方案

一个算法A称为(1+ε)因子近似算法,如果极小化问题的一实例在算法A下得到的目标值不超过该问题的最优目标值的(1+ε)倍且运算时间是关于输入规模的多项式。一族近似算法称为全多项式近似方案(FPTAS) ,如果对于任意的ε>0,算法Aε是一(1+ε)因子近似算法且运算时间是关于输入规模及1/ε的多项式。不失一般性,令0<ε≤1。对0<ε≤1,假设bj,ej,r0,wj都是非负整数。

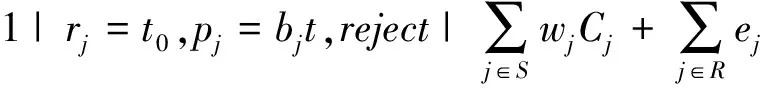
1) 将A中向量x进行标号x(1),x(2),…,x(|A|),使得0≤f(x(1))≤f(x(2))≤…≤f(x(|A|))。

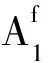
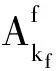
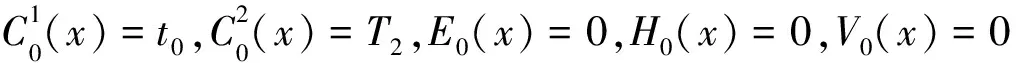
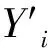
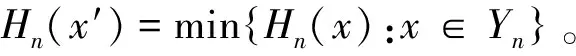
假设xj=1,令δ1=δ。

同理,当xj=0,xj=2时,有

这样导出

从式(1)和式(7)得

类似地,有

令δk=δ+δk(1+δ),k=2,3,…,n-j+1,于是有

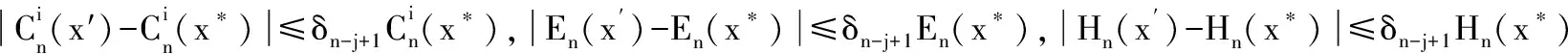
又通过引理4有

算法的时间复杂性:

3 结 论

本文研究的是带有释放时间、退化工件和拒绝工件,且机器带有不可用区间的单机排序问题,目标函数为最小化所有接受工件的加权总完工时间与所有拒绝工件的拒绝惩罚之和。首先说明该问题是一般意义下NP-难的,进而利用划分程序的方法给出了一个全多项式近似方案,最后确定了其时间复杂性为O(n7L5/ε4)。由于机器带有不可用区间以及拒绝惩罚同时存在的现象很普遍,因此,进一步研究机器带有不可用区间以及拒绝惩罚的排序问题具有广泛的应用价值和实际意义。对于具有其他退化效应的函数问题以及机器具有不可用区间的排序问题,还有待进一步研究。

[1]MOSHEIOV G.Scheduling jobs under simple linear deterioration[J].Comput Ope Res, 1994,21(6):653-659.

[2]WU C C, HSU P H, CHEN J C, et al.Genetic algorithm for minimizing the total weighted completion time scheduling problem with learning and release times[J].Comput Ope Res, 2011,38(7):1025-1034.

[3]崔苗苗,赵玉芳,王松丽.机器具有可用性限制的加权总完工时间问题[J].沈阳师范大学学报:自然科学版, 2012,30(2):157-163.

[4]CHENG Yushao, SUN Shijie.Scheduling linear deteriorating jobs with rejection on a single machine[J].Eur J Oper Res, 2009,194(1):18-27.

[5]ZHANG Liqi, LU Lingfa, YUAN Jinjiang.Single machine scheduling with release dates and rejection[J].Eur J Oper Res, 2009,198(3):975-978.

[6]LI Shisheng, YUAN Jinjiang.Parallel-machine scheduling with deteriorating jobs and rejection[J].Theor Comp Sci, 2010,411(40):3642-3650.

[7]JI Min, CHENG T C E.Parallel-machine scheduling with simple linear deterioration to minimize total completion time[J].Eur J Oper Res, 2008,188(2):342-347.

[8]王吉波,王建军,何平.具有共同松弛时间的恶化型工件排序问题研究[J].大连理工大学学报, 2012,52(3): 932-936.

[9]王吉波,刘璐,许扬韬,等.具有恶化工件的不同工期指派问题研究[J].沈阳航空航天大学学报, 2013,30 (5):83-87.

[10]KACEM I, HAOUARI M.Approximation algorithms for single machine scheduling with one unavailability period[J].Oper Res, 2009,7(1):79-92.

[11]WU C C, LEE W C.Scheduling linear deteriorating jobs to minimize makespan with an availability constraint on a single machine[J].Infor Proc Let, 2003,87(2):89-93.

[12]LEE C Y.Machine scheduling with an availability constraint[J].J Glo Opt, 1996,9(3/4):395-416.

[13]LEE C Y.Minimizing the makespan in the two-machine flowshop scheduling problem with an availability constraint[J].Oper Res Let, 1997,20(3):129-139.

[14]CHEN W J.Minimizing total flow time in the single-machine scheduling problem with periodic maintenance[J].J Oper Res Soc, 2006,57(4):410-415.

[15]JI Min, HE Yong, CHENG T C E.Scheduling linear deteriorating jobs with an availability constraint on a single machine[J].Theor Comp Sci, 2006,362(1):115-126.

[16]KOVALYOV M Y, KUBIAK W.A fully polynomial approximation scheme for the weighted earliness-tardiness problem[J].Oper Res, 1999,47(5):757-761.

Single machine scheduling with rejection for minimizing total weighted completion time

YANLijun,ZHAOYufang

(School of Mathematics and Systems Science, Shenyang Normal University, Shenyang 110034, China)

Traditional scheduling problems assume that the processing time of a given job is fixed.However, the processing time may change in the real world.At the same time, the machine may ba unavailable because of preventive maintenances and periodical repairs, namely, non-availability interval.This paper studied the scheduling problems with release dates, deteriorating effect, rejection and an availability constraint.In this model, job processing times are not fixed because jobs may deteriorate while wating to be precessed.We consider the processing time of a job is related with its starting time and jobs can be rejected.A job is either rejected, in which case a rejection penalty has to be paid.The objective is to minimize the total weighted completion time of the accepted jobs plus the total penalty of the rejected jobs.First, we indicate the problem is NP-hard in the ordinary sense.And then, a fully polynomial-time approximation scheme is given for the problem, and analyse the time complexity of the fully polynomial-time approximation scheme.

rejection penalty; deteriorating; fully polynomial time approximation scheme; non-availability interval

2014-05-23。

辽宁省教育厅科学技术研究项目(L2014433)。

闫力君(1990-),女,辽宁铁岭人,沈阳师范大学硕士研究生; 通信作者: 赵玉芳(1966-),女,辽宁辽阳人,沈阳师范大学副教授,博士,硕士研究生导师。

1673-5862(2015)01-0033-05

O223

A

10.3969/ j.issn.1673-5862.2015.01.008