天然气非线性复合渗流数学模型

张笑洋, 王晓冬, 董文秀, 王家航, 王 磊

(1.中国地质大学(北京) 能源学院，北京 100083；2.中国地质大学(北京) 非常规天然气地质评价及开发工程重点实验室，北京 100083 )



天然气非线性复合渗流数学模型

张笑洋1,2, 王晓冬1, 董文秀1, 王家航1, 王 磊1

(1.中国地质大学(北京) 能源学院，北京 100083；2.中国地质大学(北京) 非常规天然气地质评价及开发工程重点实验室，北京 100083 )

在对油气井进行水力压裂后产生的有限导流垂直裂缝进行研究时，特别是对于泄流面积比较狭长的储层，可采用复合流动模型求解得到接近于实际的近似结果.利用演绎一维流动数学模型，考察天然气渗流的非线性影响，并定义拟时间因子化简控制方程，利用Laplace变换求得无量纲解析解式，联立物质平衡方程后分析拟时间因子的变化规律及其对生产动态的影响.进而利用复合渗流模型分析垂直裂缝气井在定流量和定流压生产的2种典型制度下的动态表现特征，绘制相应的不稳态压力及产量曲线，并采用商业模拟器(Eclipse)对该解析解进行模型的对比验证.结果表明：天然气非线性渗流特点对拟稳态时期的产量及压力特征有较大影响.该研究结果有利于提高对天然气渗流规律的认识，为压裂气井的生产动态分析提供一定的理论参考.

非线性； 天然气； 复合流动模型； 渗流规律

0 引言

对油气井进行水力压裂产生有限导流垂直裂缝，已成为一种常态的增产措施.然而，有限导流垂直裂缝所引起的不稳态渗流问题有些复杂，通常需要求解地层流动和裂缝流动耦合的积分方程.在某些情况下，采用分区简化的复合流动模型能够避免积分方程的出现，得到一种近似结果，特别对于泄流面积比较狭长的储层，该模型更接近于实际.在复合流动模型方面，Fraim M L和Wattenbavger R A等[1-2]认为致密气藏中的生产井经过水力压裂后，在很长一段时间内储层中以一维流动为主，并采用一维流动模型对气井进行产量递减分析.Cinco L H等[3-4]提出双线性复合模型，用以分析垂直裂缝井的早期流动特征.Lee W J, Lee S T, Azari M等[5-8]提出三线性流模型.Brown M等[9]利用三线性流模型对致密气及页岩气的多级压裂水平井进行动态分析，但忽略系统压力对气体压缩因子及黏度的影响.Meyer B R等[10]根据Lee W J等提出的三线性流模型解析解，结合拟稳态电阻率模型,对页岩气进行多级压裂水平井裂缝优化.Brohi I等[11]针对致密气藏和页岩气藏建立压裂水平井双孔复合三线性流数学模型.Stalgorova E等[12-13]建立多级压裂水平井三线性渗流模型，并应用于对非常规油气藏的研究，该模型也未考虑系统压力对气藏参数的影响及其引起的求解结果的误差.我国对线性复合模型的研究有一定发展，将线性复合模型应用于对有限导流垂直裂缝直井或多级压裂水平井的研究[14-24]，但均未充分考虑天然气非线性渗流特征，其结果必然产生一定偏差.

首先，笔者演绎一维流动数学模型，在考察天然气渗流的非线性影响，通过定义拟时间因子化简控制方程，并利用Laplace变换求得无量纲解析解式，联立物质平衡方程分析拟时间因子的变化规律及其对生产动态的影响.其次，根据一维流动模型的研究结果，利用复合渗流模型分析垂直裂缝气井在定流量和定流压生产的2种典型制度下的动态表现特征，绘制相应的不稳态压力及产量曲线.最后,利用商业模拟器(Eclipse)对该解析解进行模型的对比验证.

1 一维非线性不稳态渗流控制方程及其化简

在常规砂岩储层中，一般情形下天然气的等温压缩因子比孔隙介质的等温压缩因子大一个数量级以上.因此，在等温条件下，忽略孔隙介质弹性，联立质量守恒方程和运动方程，得到天然气的一维不稳态渗流方程为

(1)

式中：Kg为介质渗透率；p为压力；μg为天然气黏度；Z为偏差因子；t为延续时间；x为横坐标；φ为孔隙度；Swi为束缚水饱和度；αt为单位换算因数(αt=3.6×24×10-3).

显然，由于天然气的黏度μg(p)和偏差因子Z(p)是系统压力p的非线性函数，因此式(1)是非线性的.若定义拟压力函数：

(2)

式中：μgi与Zi分别为初始条件下的天然气黏度和偏差因子；pP与pi分别为拟压力和原始地层压力.其中μgi=μg(pi)，Zi=Z(pi)，则式(1)化简为

(3)

式中：cg为天然气压缩因子.

在式(3)中，由于右端μg(p)cg(p)是系统压力p的非线性函数，因此式(3)还是非线性方程.若将μg(p)cg(p)强行近似为某一常数，则式(3)与对应的微可压缩液体流动具有相同的形式——“液体渗流模式”，是一种比较勉强的近似.若定义β(t)为拟时间因子[25]，即

(4)

式中：cgi为初始条件下的天然气压缩因子，cgi=cg(pi)，则式(1)简化为

(5)

式(5)与“液体渗流模式”形式相同，虽然右端微分中多了拟时间因子β(t)，但已能进行解析求解.这里式(5)是式(1)的近似简化结果[5].

2 一维流动产量递减分析

为考察拟时间因子β(t)的变化规律及其对产量递减规律的影响，采用Wattenbarger R A一维流动产量递减解析模型进行计算和分析.Wattenbarger R A等[2]认为，许多致密气藏中的生产井，经过水力压裂后，在很长一段时间内储层中以一维流动为主，可以采用一维流动模型进行生产数据分析.

一维渗流物理模型见图1.其中，在厚度为h、长度为ye、宽为xe的封闭地层中，其中心存在贯穿的、半长为xf的均匀流量垂直裂缝，即裂缝长度等于地层宽度(2xf=xe).当垂直裂缝以常流压pwf生产时，引发储层产生等温不稳定渗流过程.定义无量纲量，即

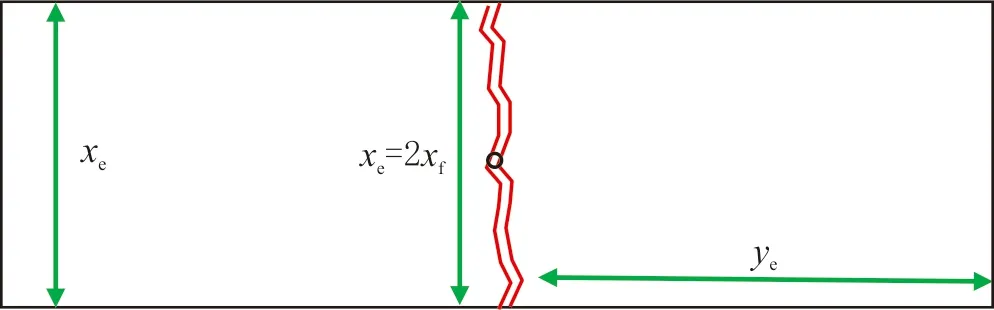
图1 一维渗流物理模型Fig.1 The physical model of one-dimensional flow

式中：qg为标准状况下井的产量；Bgi=(pscZiTi)/(piZscTsc)(其中，psc为标准状况压力(0.101 325 MPa)；Tsc为标准状况温度(293.15 K)；Zsc为标准状况偏差因子；Ti为储层温度)；y为纵坐标；ye为纵向泄流边界；xf为垂直裂缝半长；αp、αt为单位换算因数(αp=2π×3.6×24×10-7,αt=3.6×24×10-7).

一维不稳态渗流控制方程为

(6)

定解条件为

(7)

利用Laplace变换求解得

(8)

分析式(8)表明，在晚期阶段，有

(9)

在早期阶段，有

(10)

虽然得到无量纲解式(8-10)，但进行实际产量计算时，需要确定拟时间因子β(t)的变化规律.参考Fraim M L等[1]的方法，对于β(t)取近似式为

(11)

式中：pavg为储层平均压力.

式(11)能够获得较高的准确性，但在不稳定渗流过程中，储层平均压力pavg是随时间变化的，可通过联立物质平衡方程得到.常规气藏的物质平衡方程为

(12)

式中：Gp为天然气累计产量，可通过数值积分得到；Gsc为天然气地质储量.

对于生产过程有0<β(t)≤1，若记β(t)中的被积函数为λ(t)，即

(13)

则λ(t)与β(t)之间的关系为

t.

(14)

根据两者的定义，联立式(11)和式(12)，计算得到λ(t)和β(t)的变化曲线(见图2).

图2表明，在初始阶段可以忽略储层平均压力递减，λ(t)≈1.0，β(t)≈1.0，气体渗流行为近似于微可压缩液体的渗流行为；当渗流进入晚期拟稳态阶段时，pavg快速递减，气体渗流行为将逐渐偏离微可压缩液体的渗流行为.

计算式(8)得到一维流动模型产量递减曲线(见图3).图3表明，在后期渗流状态达到拟稳态阶段时，气体与微可压缩液体的产量q递减趋势将出现较大差别.当泄流边界大小相同时，随着储层平均压力pavg的递减，同一时间点所对应的气体产量高于相同条件下微可压缩液体产量.

3 垂直裂缝气井产量递减分析

对于中高渗砂岩储层，如果储层有效泄流区域比较狭长，采用线性复合渗流模型描述不稳定渗流过程较为合适，可避免数值求解地层与裂缝耦合所形成的积分方程.

图2 参数λ(t)与β(t)的变化曲线Fig.2 Curves of λ(t) and β(t) values

图3 一维流动模型产量递减曲线Fig.3 Production decline curve of one-dimensional flow model

3.1 非线性复合流动数学模型

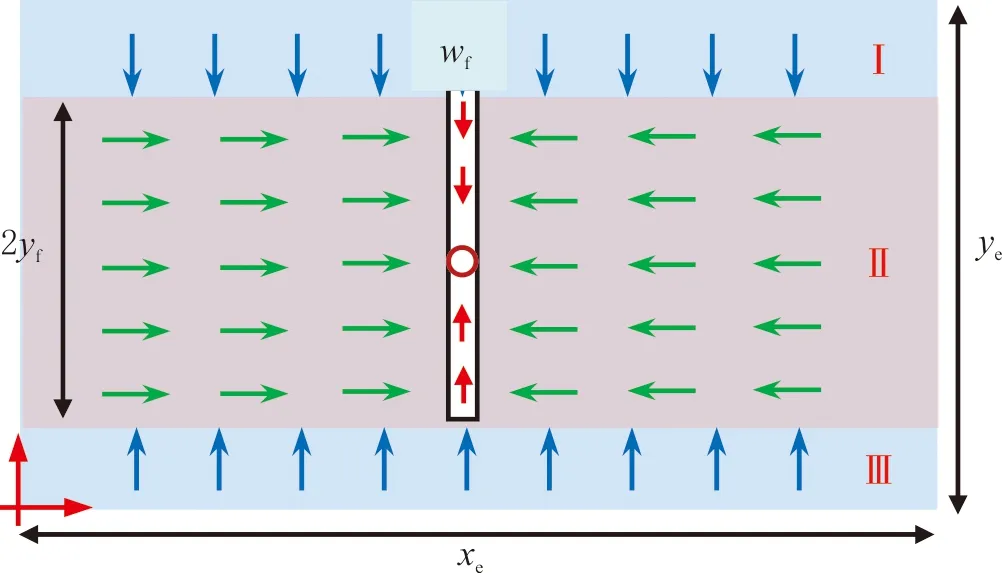
图4 垂直裂缝井线性复合流动模型Fig.4 The linear compound flow model for vertical fractured wells

在均质矩形封闭气藏中心存在一口带有对称双翼的有限导流垂直裂缝井，裂缝垂向完全穿透储层，即裂缝高度等于储层厚度；常规天然气由储层流入裂缝，再经裂缝流入井筒；井以常流压生产，诱发储层产生等温渗流过程.坐标原点位于储层左下角(见图4).

根据关于拟时间因子β(t)的定义，地层渗流过程的无量纲控制方程为

(15)

定解条件为

pD(xD,yD,0)=0;

(16)

(17)

(18)

按照图4的分区方法，在区域Ⅰ和Ⅱ中，分别记pD=pⅠD和pD=pⅡD，式(15)可以按分区简化为一维方程.

(1)在区域Ⅰ中，地层只发生平行于裂缝壁面(y方向)的线性流动，式(15)简化为

(19)

初始条件为

pⅠD(xD,yD,0)=0.

(20)

边界条件为

(21)

分区界面条件为

(22)

(23)

(2)在区域Ⅱ中，由于地层主要发生垂直于裂缝壁面的线性流动，即x方向流动占优，对式(15)实施积分平均，将其简化为垂直于裂缝壁面的线性渗流，即

利用式(22)和式(23)得到

(24)

初始条件为

pⅡD(xD,yD,0)=0.

(25)

边界条件为

(26)

分区界面条件为

(27)

(28)

(3)在裂缝中，流体发生稳态渗流且具有对称性，其无量纲控制方程为

(29)

边界条件为

(30)

(31)

(32)

(33)

式(32)中:cfD为无量纲裂缝导流能力.

考虑到与井的整个有效泄流面积相比，裂缝宽度比较小，可以在裂缝内沿x方向对方程取积分平均(积分后压力函数仍记为pfD)，即

再利用式(31)和式(28)，式(29)简化为

(34)

外边界条件为

(35)

内边界条件分别为定流量或定流压，为

(36)

(37)

3.2 模型求解及计算分析

在对式(19-37)进行求解时，利用Laplace变换，求解井底定流量条件下裂缝中压力分布及定流压条件下的井底流量，分别为

(38)

(39)

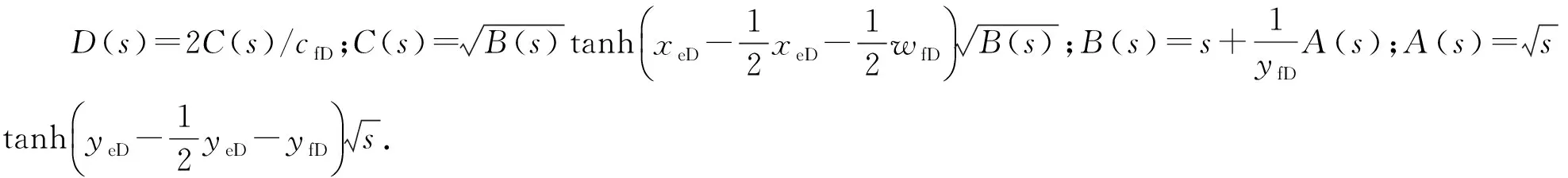
(40)

定流压条件下的井底流量为

(41)

根据式(11)及定容气藏物质平衡方程式(12)，分别在定产量和定流压条件下确定每个时间步骤的pavg和β，进行Stehfest数值反演后，绘制利用三线性流模型求解的该气藏压力及产量随时间变化的曲线.若不考虑天然气非线性渗流特点，即忽略扩散系数随时间变化时，β=1，可以得到液体模式的控制方程，对它进行Laplace变换后得到相应的液体模式解.

为了说明天然气非线性扩散的影响，分别在定流量及定流压条件下绘制流压及产量特征曲线(见图5和图6)，并将液体模式解与气体解析解进行对比，参数见表1.

表1 气藏基本参数Table 1 Basic parameters of the gas reservoir

由图5和图6可知，在气藏生产中早期气体解析解与液体模式解的特征曲线重合，气体渗流行为近似于微可压缩液体的渗流行为.这是由于对于液体λ=β=1，而在早期不稳态渗流条件下，对于气体也存在λ≈β≈1.在早期储层压力递减未波及至边界前，液体模式解与气体解析解曲线拟合较好，储层压力递减较少，不对天然气压缩因子及黏度产生太大影响.在后期压力降触及边界后，即当渗流进入晚期拟稳态阶段时，两者产生较大的差别，气体渗流行为将逐渐偏离微可压缩液体的渗流行为.此时，随着气藏压力递减幅度的上升，天然气性质发生较大变化(λ<β<1),而微可压缩液体在拟稳态阶段仍保持固有性质(λ=β=1).对于考虑天然气非线性特征的气体解析解(见图7)，在拟稳态时期的压力下降及产量递减出现滞后于液体模式解的现象，即当泄流边界大小相同时，同一时间点所对应的气体解的压降要低于液体模式解的，其产量相反.

为了验证对天然气非线性控制方程线性化处理的正确性，将文中所得气体解析解与数值模拟(Eclipse)所得结果进行对比(见图8).图8表明，解析解与数值解拟合良好，可见文中所求考虑天然气非线性扩散的解析解可以较为严格地应用于气藏动态分析.

图5 压力降落曲线Fig.5 Comparison of pressure drawdown curves

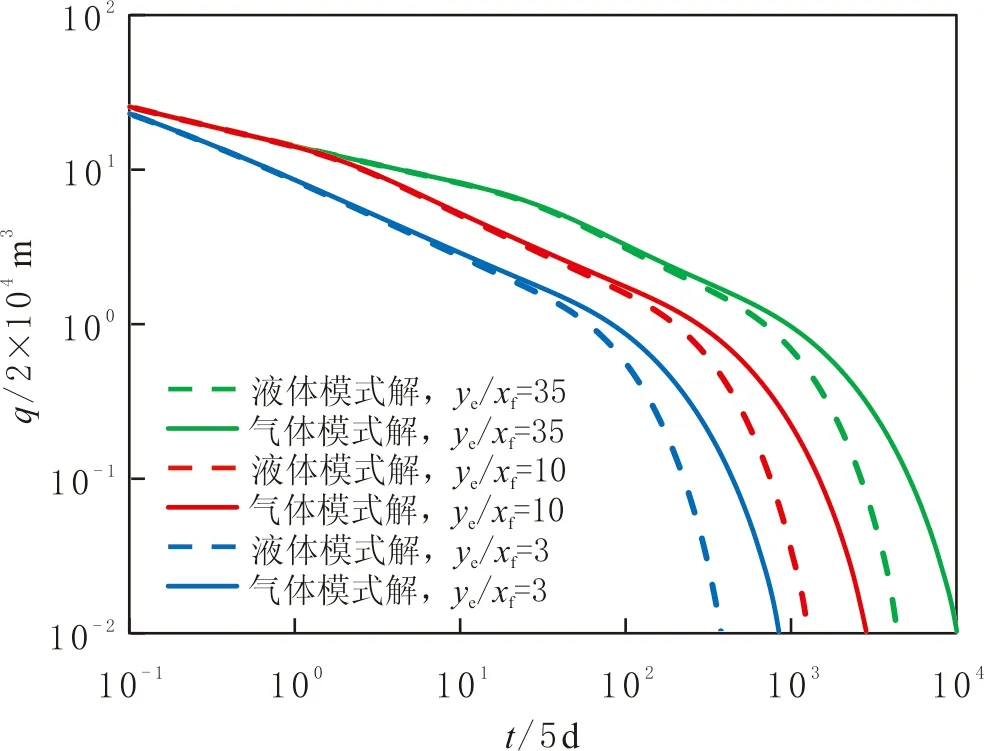
图6 产量递减曲线Fig.6 Comparison of production decline curves

图7 压力降落解析结果与数值解Fig.7 Comparison of analytical and numerical solutions to pressure drawdown

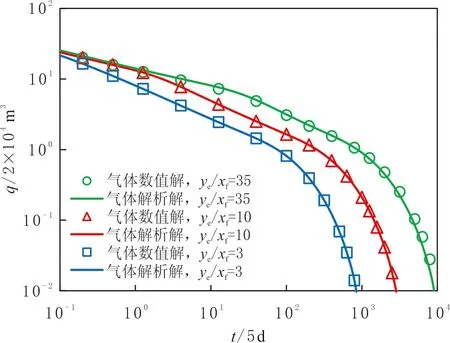
图8 产量递减解析结果与数值解Fig.8 Comparison of analytical and numerical solutions to production decline

4 结论

(1)通过演绎一维流动数学模型，考察天然气渗流的非线性影响，并联立物质平衡方程，计算及分析拟时间因子的变化规律及其对生产动态的影响.

(2)在考虑气体渗流过程中，由于天然气的等温压缩因子及黏度等参数为压力的函数，在对气藏进行开采过程中，系统压力不断递减，天然气物性参数不断发生变化.通过定义拟压力及拟时间因子，化简天然气渗流控制方程，从而得到可将其进行线性解析求解所需形式.

(3)将一维流动模型的研究结果扩展至对有限导流垂直裂缝井的研究方面，利用复合渗流模型，分析垂直裂缝气井在定流量和定流压生产的动态表现特征，绘制不稳态压力及产量曲线，并利用数值模拟结果对该解析结果进行对比验证.在考虑天然气非线性渗流特点时，尤其对具有封闭边界的气藏，在系统达到拟稳态阶段后，不可忽略天然气渗流的非线性特征对计算结果产生的影响.

[1] Fraim M L, Wattenbarger R A.Gas reservoir decline curve analysis using type curves with real gas pseudo-pressure and pseudo-time [J].Formation Evaluation, SPE 14238, 1987.

[2] Wattenbarger R A, Ahmed H El, Mauricio E V, et al.Production analysis of linear flow into fractured tight gas wells [C].SPE 39931, 1998.

[3] Cinco L H, Samaniego V F, Dominguez A N.Transient pressure behavior for a well with a finite-conductivity vertical fracture [C].SPE 6014, 1978.

[4] Cinco L H, Satnaniego V F.Transient pressure analysis for fractured wells [C].SPE 7490, 1981.

[5] Lee W J, Holditch S A.Application of pseudotime to buildup test analysis of low-permeability gas wells with long-duration wellbore storage distortion [C].SPE 9888, 1982.

[6] Lee S T, Brockenbrough J R.A new approximate analytic solution for finite-conductivity vertical fractures [J].Formation Evaluation, SPE 12013, 1986.

[7] Azari M, Wooden W O, Coble L E.A complete set of Laplace transforms for finite-conductivity vertical fractures under bilinear and trilinear flows [C].SPE 20556, 1990.[8] Azari M, Wooden W O, Coble L E.Further investigation on the analytic solution for finite-conductivity vertical fractures [C].SPE 21402, 1991.

[9] Brown M, Ozkan E, Raghavan R, et al.Practical solutions for pressure transient responses of fractured horizontal wells in unconventional reservoirs [C].SPE 125043, 2009.

[10] Meyer B R, Bazan L M, Jacot R H, et al.Optimization of multiple transverse hydraulic fractures in horizontal wellbores [C].SPE 131733, 2010.

[11] Brohi I, Pooladi D M, Aguilera R.Modeling fractured horizontal wells as dual porosity composite reservoirs-application to tight gas, shale gas and tight oil cases [C].SPE 144057, 2011.

[12] Stalgorova E, Mattar L.Practical analytical model to simulate production of horizontal wells with branch fractures [C].SPE 162515, 2012.

[13] Stalgorova E, Mattar L.Analytical model for history matching and forecasting production in multifrac composite systems [C].SPE 162516, 2012.

[14] 程博,刘常红,翟云芳,等.定井底流压下有限导流垂直裂缝井的理论模型[J].大庆石油地质与开发,2003,22(3):55-57.Cheng Bo, Liu Changhong, Zhai Yunfang, et al.Theoretical model for a well with a finite-conductivity vertical fracture on constant bottom-hole pressure [J].Petroleum Geology & Oilfield Development in Daqing, 2003,22(3):55-57.

[15] 严涛,贾永禄,张秀华,等.考虑表皮和井筒存储效应的有限导流垂直裂缝井三线性流动模型试井分析[J].油气井测试,2004,13(1):1-3.Yan Tao, Jia Yonglu, Zhang Xiuhua, et al.Trilinear flow model test analysis of finite conductivity vertical fracture wells taking the effects of skin and wellbore storage into consideration [J].Well Testing, 2004,13(1):1-3.

[16] 李爱芬,刘照伟,杨勇.双重介质中有限导流垂直裂缝井试井模型求解新方法[J].水动力学研究与进展,2006,21(2):217-222.Li Aifen, Liu Zhaowei, Yang Yong.New approach to welltest interpretion model with finite conductivity vertical fracture in double porosity reservoirs [J].Journal of Hydrodynamics, 2006,21(2):217-222.

[17] 张大为,曾昭英.有限导流垂直裂缝双线性流动模型的应用[J].特种油气藏,2007,14(4):72-75.Zhang Dawei, Zeng Zhaoying.The application of bilinear flow model for finite conductivity vertical fracture [J].Special Oil and Gas Reservoirs, 2007,14(4):72-75.

[18] 王海涛,张烈辉.有限导流垂直裂缝产能及影响因素研究[J].西南石油大学学报:自然科学版,2009,31(3):78-82.Wang Haitao, Zhang Liehui.Study on the productivity and affecting factors of finite conductivity vertical fracture [J].Journal of Southwest Petroleum University: Science & Technolygy Edition, 2009,31(3):78-82.

[19] Zhang Liehui, Guo Jingjing, Liu Qiguo.A new well test model for a two-zone linear composite reservoir with varied thicknesses [J].Journal of Hydrodynamics, 2010,22(6):804-809.

[20] 姚军,殷修杏,樊冬艳,等.低渗透油藏的压裂水平井三线性流试井模型[J].油气井测试,2011,20(5):1-5.Yao Jun, Yin Xiuxing, Fan Dongyan, et al.Trilinear flow testing model of fractured horizontal well in low permeability reservoirs [J].Well Testing, 2011,20(5):1-5.

[21] 苏玉亮,王文东,盛广龙.体积压裂水平井复合流动模型[J].石油学报,2014,35(3):504-510.Su Yuliang, Wang Wendong, Sheng Guanglong.Compound flow model of volume fractured horizontal well [J].Acta Petrolei Sinica, 2014,35(3):504-510.

[22] 高杰,张烈辉,刘启国,等.页岩气藏压裂水平井三线性流试井模型研究[J].水动力学研究与进展,2014,29(1):108-113.Gao Jie, Zhang Liehui, Liu Qiguo, et al.Well test model of trilinear flow for fractured horizontal wells in shale gas reservoirs [J].Chinese Journal of Hydrodynamics, 2014,29(1):108-113.

[23] 田冷,肖聪,刘明进,等.考虑页岩气扩散的多级压裂水平井产能模型[J].东北石油大学学报,2014,38(5):93-102.Tian Leng, Xiao Cong, Liu Mingjin, et al.Productivity model for multi-stage fractured horizontal well for shale gas reservoirs taking diffusion into consideration [J].Journal of Northeast Petroleum University, 2014,38(5):93-102.

[24] 王家航,侯晓春,王晓冬,等.河道型低渗透储层有限导流垂直裂缝井动态特征[J].东北石油大学学报,2015,38(4):72-79.Wang Jiahang, Hou Xiaochun, Wang Xiaodong, et al.Performance of vertical fractured wells with finite conductivity in channel-type reservoirs with low permeability [J].Journal of Northeast Petroleum University, 2015,38(4):72-79.

[25] Peng Ye, Luis F, Ayala H.A density-diffusivity approach for the unsteady state analysis of natural gas reservoirs [J].Journal of Natural Gas Science and Engineering, 2012,7(4):22-24.

2015-06-05；编辑：关开澄

国家科技重大专项(2011ZX05009-004)

张笑洋(1991-)，女，博士研究生，主要从事油气田开发方面的研究.

TE348

A

2095-4107(2015)04-0079-09

DOI 10.3969/j.issn.2095-4107.2015.04.010