推广的F/G-展开法及其应用

胡武强，张金良

(河南科技大学 数学与统计学院，河南 洛阳 471023)



推广的F/G-展开法及其应用

胡武强，张金良

(河南科技大学 数学与统计学院，河南 洛阳 471023)

首先推广了F/G-展开法，使之能应用于变系数微分方程的求解中。作为推广的F/G-展开法应用实例，本文在非对称势阱下，求解了(3+1)-维三次-五次 Gross-Pitaevskii 方程。导出了方程含有较多任意参数的双曲函数形式精确解、三角函数形式周期波解，得到了孤波的传播速度及啁啾随时间的变化规律。

(3+1)-维三次-五次Gross-Pitaevskii方程；F/G-展开法；精确解；传播速度；啁啾

0 引言

考虑如下形式的变系数Gross-Pitaevskii方程[1-5]：

(1)

本文首先介绍推广的F/G-展开法；然后，利用推广的F/G-展开法求解方程(1)；最后，得出结论。

1 F/G-展开法的推广

1.1 推广的F/G-展开法

推广的F/G-展开法描述如下。

假定一个变系数非线性方程为：

Ψ(u,ut,ux,utt,uxt,uxx,…)=0，

(2)

其中:u=u(x,t)是一个未知函数；Ψ是u(x,t)及其各阶偏导数的一个多项式且含有最高阶的偏导项、非线性项。

假设方程(2)的解可以用一个含(F/G)的多项式表示为：

(3)

其中:F=F(ξ)、G=G(ξ)满足线性常系数微分方程组

F′=λG，G′=μF，

(4)

其中：αm,αm-1,…,α0；p和q是只含t的函数；λ和μ是常数；ξ0是一个任意的常数；m由方程(2)中出现的最高阶偏导项、非线性项之间的齐次平衡确定[16-19]。

将式(3)代入到方程(2)，并利用微分方程组(4)，合并(F/G)同次幂，方程(2)的左边化成一个(F/G)的多项式，令该多项式的系数为零，得到一组关于αm、αm-1、…、α0、p、q以及常数λ和μ的非线性方程组。解该方程组并将所得结果代入式(3)中，利用式(4)的解，可得非线性方程(2)的精确解。

1.2 方程组(4)的精确解

情形1 若λ>0,μ>0,

情形2 若λ<0,μ<0,

情形3 若λ>0,μ<0,

情形4 若λ<0,μ>0,

2 求解变系数Gross-Pitaevskii方程

令

u(x,y,z,t)=A(x,y,z,t)exp[iB(x,y,z,t)]，

(5)

将式(5)代入式(1)，实虚分离后，得到A(x,y,z,t)、B(x,y,z,t)满足：

(6)

(7)

令

(8)

由式(8)，得到ρ、B满足的方程组：

ρt+β[ρxBx+ρyBy+ρzBz+ρ△B]=2γρ，

(9)

2χ1ρ3+2χ2ρ4+2Vρ2=0。

(10)

由齐次平衡原则[16-18]，假设方程组(9)～(10)的解如下：

(11)

B=a1(t)x2+a2(t)y2+a3(t)z2+b1(t)x+b2(t)y+b3(t)z+e(t)，

(12)

其中：

ξ=k1(t)x+k2(t)y+k3(t)z+ω(t)，

(13)

且f1(t)、f2(t)、a1(t)、a2(t)、a3(t)、b1(t)、b2(t)、b3(t)、e(t)、k1(t)、k2(t)、k3(t)、ω(t)待定，F(ξ)、G(ξ)满足方程组(4)。

将式(11)～式(13)代入方程组(9)～(10)中，令方程组(9)～(10)左边各项的系数等于0，得：

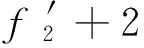
ω′+β(k1b1+k2b2+k3b3)=0；

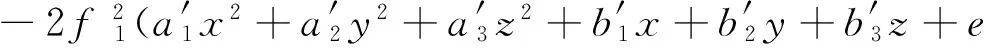
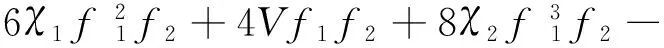
2βf1f2[(2a1x+b1)2+(2a2y+b2)2+(2a3z+b3)2]-

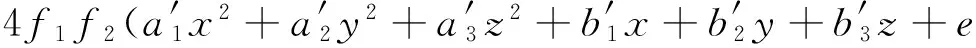
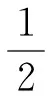
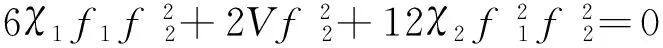
求解以上非线性方程组，得：

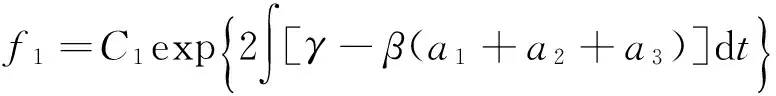
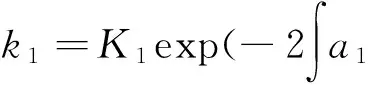
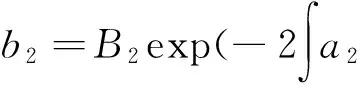
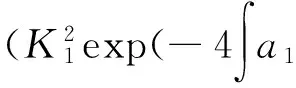
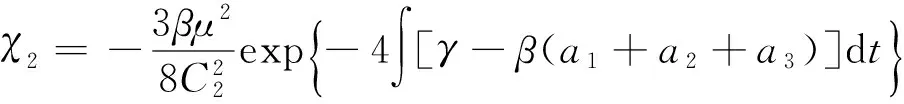
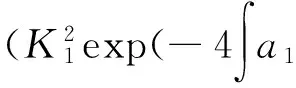
由式(5)、式(8)、式(11)～式(13)及以上结果，得方程(1)的精确解为：

(14)

B=a1(t)x2+a2(t)y2+a3(t)z2+b1(t)x+b2(t)y+b3(t)z+e(t)，

(15)

其中：

ξ=k1(t)x+k2(t)y+k3(t)z+ω(t)。

(16)

啁啾系数随时间的变化为：

令

ξ=Cξ，

即

k1(t)x+k2(t)y+k3(t)z+ω(t)=Cξ，

其中：Cξ为常数。

于是，沿x轴方向孤波的传播速度为：

沿y轴方向孤波的传播速度为：

沿z轴方向孤波的传播速度为：

注1:为了减少篇幅，文中省去了将辅助方程组(4)的解代入式(14)中，得到(3+1)-维三次-五次Gross-Pitaevskii方程(1)含有较多任意参数的双曲函数形式精确解、三角函数形式周期波解。

注2：为了减少篇幅，文中也不再讨论当Gross-Pitaevskii方程(1)的解中参数取定值时，得到Gross-Pitaevskii方程的一些特殊形式解，如亮孤子解、暗孤子解等。

3 结论

本文推广了F/G-展开法，使之可用来求解变系数微分方程的精确解。利用推广的F/G-展开法，导出了(3+1)-维三次-五次 Gross-Pitaevskii 方程含有较多任意参数的双曲函数形式精确解、三角函数形式周期波解，并得到了啁啾系数随时间的变化以及孤波的传播速度。本文提出的推广的F/G-展开法，可以应用于其他变系数微分方程的求解中。

[1] Dalfovo F，Giorgini S，Pitaevskii L P，et al．Theory of Bose-Einstein Condensation in Trapped Gases[J].Reviews of Modern Physics,1999,71:463-512.

[2]Kobayashi M,Tsubota M.Kolmogorov Spectrum of Superfluid Turbulence:Numerical Analysis of the Gross-Pitaevskii Equation with a Small-scale Dissipation[J].Physical Review Letters,2005,94:5302-5306.

[3] Zhong W P，Belicé M R，Lu Y Q，et al.Traveling and Solitary Wave Solutions to the One-Dimensional Gross-Pitaevskii Equation[J].Physical Review E,2010,81:6605-6609.

[4] Duan Y S,Hang P M.Vortex in Generalized Gross-Pitaevskii Theory[J].Nuclear Physics Review,2001,18(4):225-231.

[5] Zhao L,Yang J,Xie Q Y,et al.Topological Aspect of Vortex Lines in Two-dimensional Gross Pitaevskii Theory[J].Chinese Physics B,2012,21:090304.

[6] Dai C Q,Chen R P,Wang Y Y.Spatiotemporal Self-Similar Solutions for the Nonautonomous (3+1)-Dimensional Cubic Quintic Gross Pitaevskii Equation[J].Chinese Physics B,2012,21:030508.

[7] 石玉仁,许新建,吴枝喜,等.含时线性势Gross-Piteavskii方程的孤立波解[J].兰州大学学报:自然科学版,2007,43(4):131-135.

[8] Shi Y R,Wang X L,Wang G H,et al.Analytical Solutions for the Two-Dimensional Gross-Pitaevskii Equation with a Harmonic Trap[J].Commun Theor Phys,2013,59:273-278.

[9] Shi Y R,Liu C B,Wang G H,et al.Application of the Homotopy Analysis Method for the Gross-Pitaevskii Equation with a Harmonic Trap[J].Chinese Physics B,2012,12:120307.

[10] Hu X,Li B.Exact Analytical Solutions of Three-dimensional Gross-Pitaevskii Equation with Time Space Modulation[J].Chinese Physics B,2011,20:050315.

[11] Fei J X,Zheng C L.Exact Solutions and Localized Excitations of a (3+1)-Dimensional Gross Pitaevskii System[J].Chinese Physics B,2012,21:070304.

[12] Mei J Q,Zhang H Q.New Families of Soliton and Periodic Solutions of Bose-Einstein Condensation in Linear Magnetic Field and Time-Dependent Laser Field[J].Commun Theor Phys,2005,44:209-212.

[13] Gao Y,Lou S Y.Analytical Solitary Wave Solutions to a (3+1)-Dimensional Gross-Pitaevskii Equation with Variable Coefficients[J].Commun Theor Phys,2009,52:1031-1035.

[14] 纪庆群,陈浩.(3+1) 维3次-5次 Gross-Pitaevskii 方程在非对称势阱下的精确解[J].华南师范大学学报:自然科学版,2014,46(2):46-49.

[15]Lee Y,An J H.New Exact Solutions of Some Nonlinear Evolution Equations by Sub-ODE Method[J].Honam Mathematical Journal,2013,35:683-699.

[16] Wang M L.Solitary Wave Solutions for Variant Boussinesq Equations[J].Physics Letters A,1995,199:169-172.

[17] Zhang J L,Wang Y M,Wang M L,et al.New Application of the Homogeneous Balance Principle[J].Chinese Physics,2003,12:245-250.

[18] 黄彦辉,张金良,魏鹏波.两个变系数非线性Schrödinger的精确解[J].河南科技大学学报:自然科学版,2013，34(3):83-86.

[19] 李伟,张金良.Klein-Gordon-Schrödinger方程组的精确解[J].河南科技大学学报:自然科学版,2014,35(6):84-87.

河南省基础与前沿技术研究基金项目(092300410179);河南科技大学科研创新能力培育基金项目(2011CX011)

胡武强(1976-),男,河南宜阳人,硕士生;张金良(1966-),男,河南唐河人,教授,博士,硕士生导师,研究方向为非线性数学物理问题.

2015-04-30

1672-6871(2015)06-0091-05

O175.7

A