特征值与特征向量的两例应用

阮春蕾

(河南科技大学 数学与统计学院，河南 洛阳 471023)



特征值与特征向量的两例应用

阮春蕾

(河南科技大学 数学与统计学院，河南 洛阳 471023)

以纤维取向张量及大分子构型张量的两类矩阵为例，对其特征值与特征向量的应用进行了说明。通过采用特征值与特征向量的信息绘制出取向椭球，直观地给出纤维及大分子的形变与取向。数值计算结果表明：该方法是有效的。

特征值；特征向量；取向张量；构型张量

0 引言

特征值与特征向量是线性代数理论中的基本概念，是矩阵理论的重要组成部分，它在线性代数和其他科技领域中占据重要地位。对特征值与特征向量的应用研究，将加深学生对相关理论的理解，提高对线性代数课程的兴趣。

特征值与特征向量具有多方面的应用。例如，文献[1]采用特征值与特征向量的相关理论研究了线性微分方程的求解问题。文献[2]采用方差-协方差矩阵的特征值与特征向量研究了降水对地下水位的影响。文献[3]采用特征值研究了圆柱壳稳定性问题。文献[4]采用能量特征向量对滚锥轴承内圈松动问题进行了探讨。因此，特征值与特征向量在数学、统计学和工程技术等领域发挥着重要作用。

在力学中，惯量张量、应力张量等的分析都可归结为求解矩阵特征值与特征向量的问题。本文仅就工程实际中的两类张量—纤维取向张量和大分子构型张量展开分析，并利用其特征值与特征向量的信息，形象地给出纤维及大分子的可视化显示。需要指出的是，张量可看成是矩阵的特殊推广，二维空间中的二阶张量对应于一个二阶方阵，而三维空间中的二阶张量则对应于一个三阶方阵。

1 纤维取向张量

纤维取向张量往往在研究纤维增强复合材料力学性能时被用到，它反映的是材料在加工时的纤维取向状态，直接影响到复合材料的弹性模量、剪切模量及泊松比等。

在材料制备过程中，纤维取向张量满足下面的运动方程[5]：

(1)

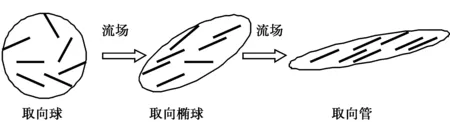
图1 纤维粒子在流场中的描述

准确预测纤维取向并控制加工过程需要对纤维统计状态进行可视化显示。当流体静止，即没有外力的情况下，纤维粒子随机分布，是各向同性的，所有可能的取向组成一个取向球。在流场的作用下，这个取向球会发生变形，形成取向椭球或取向管，如图1所示。

为了表示纤维在流场中的统计状态，需采用二阶纤维取向张量a2的信息。由表达式可知：a2对称正定。因此，可采用椭圆或椭球的方法来获得纤维的取向状态[5-7]，即：在二维时，通过计算a2对应的二阶矩阵获得其特征值及特征向量。特征向量代表主轴的方向而相应的特征值代表其所在主轴上的长度，从而获得相应的取向椭圆。在三维情况下，可通过计算a2对应的三阶矩阵获得相应的特征值及特征向量。类似地，可获得相应的取向椭球。取向椭圆或椭球代表了统计状态下纤维的取向及其概率。

(2)

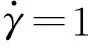
这里，由于a2的对称正定性，采用Jacobi方法[8]来计算a2的特征值与特征向量。Jacobi方法的基本思想是通过引入平面上的旋转矩阵来实现一系列的正交相似变换，并将原实对称矩阵化为对角矩阵，进而求出全部的特征值与相应的特征向量。采用C++语言编制程序，迭代终止的条件设为：变换后的对角矩阵中除对角线上的元素外，其他元素中的绝对值的最大值小于10-5。

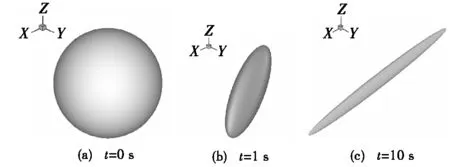
图2 不同时刻的纤维粒子取向状态

图2为不同时刻的纤维取向状态。由图2可知:不同时刻下纤维粒子取向状态相差很大。在初始时刻，由于未受到流场的作用，纤维粒子的统计状态为各向同性的取向球，即此时各向取向概率是相等的，纤维粒子随机分布在流场中。随着流场的作用，纤维粒子的统计状态发生变化，逐渐向流动方向倾斜，呈现出取向椭球和取向管，即此时纤维粒子在流动方向上的取向概率要大于其他方向的概率。这与图1的分析是一致的。采用特征值与特征向量绘制的图形能更加直观地反映粒子的统计状态。

2 大分子构型张量

在研究聚合物材料制备过程中，往往需要用到大分子构型张量。它反映的是大分子链在流场中的取向及形变情况，将直接影响到材料的弹性模量、剪切模量等。

一般而言，熔融状态下的聚合物材料可看成是悬浮聚合物大分子链的牛顿溶剂，而大分子链往往采用弹性哑铃模型来描述，即用弹簧连接两端各一个哑铃球的模型。通过受力分析，可得到哑铃球的运动方程，即Fokker-Planck方程。在假定弹簧弹力满足Perterlin近似的条件下，可得到FENE-P模型，即[9]

(3)

其中:C为大分子构型张量;λ为分子松弛时间;tr(·)为取迹;b为无量纲化的最大拉伸量。式(3)也被称为大分子构型张量的运动方程。

微观尺度上大分子链的拉伸与形变受到学者们的广泛关注。因此，其可视化显得尤为重要。事实上，当流体静止时，聚合物大分子随机分布，是各向同性的，所有可能的构型组成一个构型球。在流场的作用下，这个构型球会发生变形。如果作用力很小，构型球发生弹性形变，变成构型椭球。如果作用力很大，构型椭球将进一步变形，形成构型管，如图3所示。

图3 聚合物大分子在流场中的描述

(4)

其中：λ=0.029；b=5；C0=δ；dt=10-4。由式(4)计算获得不同时刻的C后，再利用其特征值与特征向量作出相应的图谱。

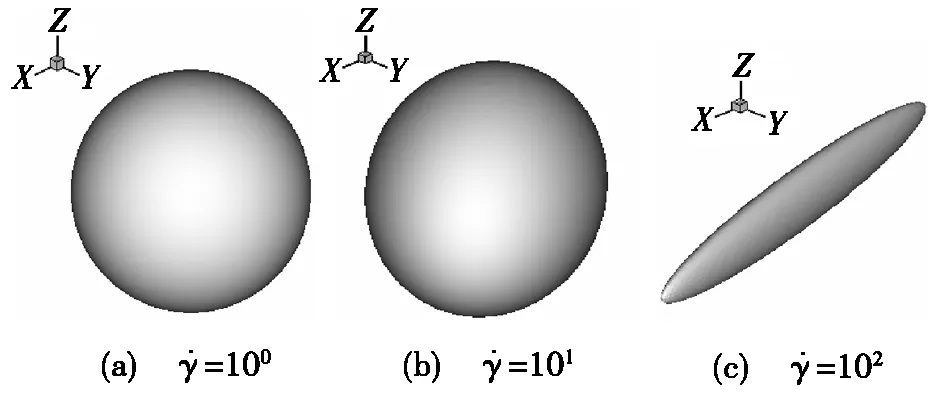
图4 不同剪切速率下的大分子取向状态

这里，由于C的对称正定性，仍然采用Jacobi方法来计算C的特征值与特征向量，迭代终止的误差限同例1。图4为不同剪切速率下的大分子取向状态。由图4可知:在剪切速率较小时，大分子链发生的形变较小，其统计状态仍然类似于构型球；而随着剪切速率的增加，大分子链发生的形变逐渐增大，并向流动方向取向，其统计状态逐渐变为构型椭球与构型管。这与图3的分析是一致的。采用特征值与特征向量绘制的图形将大分子的统计状态清晰地显示出来。

3 结论

特征值与特征向量在工程中发挥着重要作用。本文仅以力学中的纤维取向张量及大分子构型张量为例，通过其特征值与特征向量的相关信息，给出纤维及大分子的可视化显示。该方法也有望推广到更多的工程领域中。

[1] 赵晓花,李灵晓.一个四阶非线性微分算子的特征值问题[J].河南科技大学学报:自然科学版,2007,28(4):78-80.

[2] 郑小菁,刘序俨,韦永祥,等.采用主成分分析方法研究降水对地下水位的影响[J].地震,2008,28(4):91-102.

[3] 杨民献,张淑芬,王彦生.圆柱壳的屈曲荷载最大化设计[J].河南科技大学学报:自然科学版,2003,24(1):71-74.

[4] 蔡海潮,李孟源,陈春朝,等.滚锥轴承内圈松动的声发射诊断[J].河南科技大学学报:自然科学版,2007,28(3):14-17.

[5] Advani S G,Tucker C L.The Use of Tensors to Describe and Predict Fiber Orientation in Short Fiber Composites[J].J Rheol,1987,31:751-784.

[6] Ruan C L,Jie O Y.Microstructures of Fiber Suspensions in Complex Geometry[J].E-polymers,2010,10(1):1088-1100.

[7]Ruan C L,Jie O Y,Zhang H P.Numerical Study on Fiber Suspensions in Non-isothermal Viscoelastic Media[J].International Journal of Numerical Methods for Heat & Fluid Flow,2013,23(3):460-478.

[8] 李庆扬,王能超,易大义.数值分析[M].5版.北京:清华大学出版社,2008.

[9] Beris A N,Edwards B J.Thermodynamics of Flowing Systems[M].New York:Oxford University Press,1994.

国家自然科学基金项目(11402078);河南省科技攻关基金项目(122102210198);河南省教育厅科学技术研究重点基金项目(14B110020);河南科技大学青年科学基金项目(2012QN015)

阮春蕾(1983-),女,浙江临安人,讲师,博士,研究方向为偏微分方程数值解.

2014-10-06

1672-6871(2015)06-0087-04

O151.2

A