基于损伤理论的混凝土Ⅰ-Ⅱ复合型裂缝扩展角

王玉琳，王向东，韩金启，杨 林

(河海大学 力学与材料学院,江苏 南京 210098)



基于损伤理论的混凝土Ⅰ-Ⅱ复合型裂缝扩展角

王玉琳，王向东，韩金启，杨 林

(河海大学 力学与材料学院,江苏 南京 210098)

基于混凝土断裂与损伤的基本理论，进行了Ⅰ-Ⅱ复合型裂缝扩展方向研究，研究结果表明:Ⅰ-Ⅱ复合型裂缝扩展趋势是随着缝端损伤场的变化而变化的。通过缝端损伤场及损伤梯度的计算，分析了Ⅰ-Ⅱ复合型裂缝从起裂至失稳断裂裂缝扩展方向的变化规律，得到了Ⅰ-Ⅱ复合型裂缝的起裂扩展角和失稳扩展角。将其与文献结果进行对比，对比结果表明：用损伤理论研究裂缝的扩展角是可行的。

混凝土；损伤梯度；断裂；Ⅰ-Ⅱ复合型裂缝；扩展角

0 引言

混凝土由粗骨料、细骨料和水泥浆构成，加载前，颗粒和基体之间已经存在着微裂纹和微孔隙[1]。即使在较低的应力水平下，这些微裂纹也会逐渐发展，从而使混凝土的强度劣化直至产生宏观裂缝。为了确保带缝混凝土结构的安全，进行裂缝的扩展方向及其变化规律的研究具有重要的实际意义。

在混凝土裂缝扩展方向的研究中，大多应用断裂理论进行分析，但是断裂理论只能得到裂缝最终的失稳扩展方向，无法反映裂缝扩展方向从起裂至失稳扩展阶段的发展过程。由于裂缝的扩展是缝端损伤积累的结果，因此，将损伤理论应用于混凝土裂缝扩展方向的研究中，并引入损伤梯度的概念，以便得到裂缝扩展方向的变化规律。

目前，在混凝土的损伤研究中，提出了Loland损伤模型[2]、Mazars损伤模型[3]、Kachanov损伤模型[4]和Sidoroff损伤模型[5]等多种损伤模型。对单一型裂缝缝端的损伤场的研究已取得了较多的成果[6-7]。

对于Ⅰ型、Ⅱ型、Ⅲ型及Ⅰ-Ⅱ复合型裂缝的扩展角的研究大多是基于断裂理论的[8-9]，从损伤的角度去研究裂缝的扩展角以及裂缝扩展规律[10]的成果较为少见。本文应用Loland损伤模型，以损伤梯度为切入点，进行Ⅰ-Ⅱ复合型裂缝扩展方向的研究。研究结果表明：Ⅰ-Ⅱ复合型裂缝扩展方向随着缝端损伤场的变化而变化。根据Ⅰ-Ⅱ复合型裂缝从损伤至断裂阶段裂缝扩展方向的变化规律，确定了裂缝扩展角的扩展趋势，并计算得到Ⅰ-Ⅱ复合型裂缝的起裂及失稳扩展角，将其与已有的经典断裂理论和试验所得到的结果进行对比，以验证应用缝端损伤研究裂缝扩展方向的可行性。

1 基于断裂理论的Ⅰ-Ⅱ复合型裂缝的断裂角

根据叠加原理得到Ⅰ-Ⅱ复合型裂缝端区域的应力[11]为：

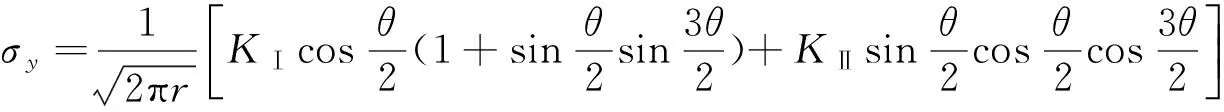
(1)

式中：r为裂缝尖端附近区域内任一点的半径；θ为斜截面的外法线与x轴间的夹角；KⅠ、KⅡ分别为Ⅰ型、Ⅱ型裂缝的应力强度因子。

由式(1)可以得到Ⅰ-Ⅱ复合型裂缝端部区域的极坐标的应力分量[12]：

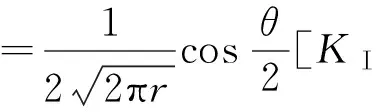
(2)

图1 r=r0的微小圆周上各点的周向应力

基于最大周向应力断裂判据，可以得到计算Ⅰ-Ⅱ复合型裂缝的开裂角θ0的方程，圆周上各点的周向应力如图1所示。

(3)

由式(3)求出Ⅰ-Ⅱ复合型裂缝的扩展角θ0为：

(4)

式(4)即为由断裂理论得到的Ⅰ-Ⅱ复合型裂缝的最终开裂角。

根据文献[9]中的试验，取KⅠ=0.58KⅡ，ν=0.145，可以求得两个扩展角分别为60°和82°。当θ0取82°时，周向应力取得最大值，由此可以确定82°是最终的失稳扩展角。

由式(4)得到的Ⅰ-Ⅱ复合型裂缝的扩展角是裂缝最终的失稳扩展角，而裂缝的发展具有连续性，式(4)并不能反映从起裂至失稳阶段裂缝的扩展趋势及其变化规律。因此，本文应用Loland损伤模型[2]，以损伤梯度为切入点，进行Ⅰ-Ⅱ复合型裂缝扩展方向变化规律的研究。

2 Ⅰ-Ⅱ复合型裂缝缝端损伤场分析

文献[2]在对混凝土等脆性材料的试验结果进行对比研究后发现：当应力将要达到峰值应力时，应力与应变之间的关系不再是线性关系。这表明在达到最大应力以前，材料的内部已经存在一定的损伤。

Loland损伤模型[2]考虑了混凝土材料的初始损伤D0，当应力临近峰值应力时，应变曲线开始偏离直线，标志着初始裂缝已经开始扩展。利用混凝土的拉伸应力-应变曲线，拟合可以得到材料损伤方程[13]：

(5)

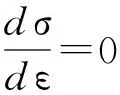
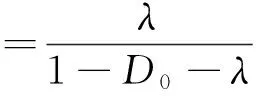
根据文献[9]可知：普通混凝土材料的初始损伤D0可取0.05；混凝土的峰值应力和与之对应的应变可分别取σf=2.5MPa和εf=10-4；拉伸强度为σu=3.0MPa；极限拉应变为εu=5×10-4；弹性模量取E0=3.5×104MPa；泊松比ν=0.145。

由此可得C1=3.13×1014，C2=1 418， β=3.8。把求得的参数代入式(5)得：

(6)

图2 损伤D(ε)与应变ε的关系曲线

根据式(6)可以得到缝端损伤和应变的关系曲线，如图2所示。从图2中可以看出：损伤是随着应变的增大而增大的，即随着荷载的增加，应变随之增大，缝端损伤区域逐渐扩展，裂缝的扩展方向发生改变。

3 基于损伤梯度的Ⅰ-Ⅱ复合型裂缝扩展角

3.1 Ⅰ-Ⅱ复合型裂缝损伤梯度

随着荷载的增加，裂缝损伤区域逐渐扩展，裂缝的扩展角也逐渐扩大[14]。为了更好地描述裂缝扩展角的扩展趋势，将Ⅰ-Ⅱ复合型裂缝简化为平面问题，则Ⅰ-Ⅱ复合型裂缝的损伤梯度表达式可以表示为：

(7)

由式(1)可以得到Ⅰ-Ⅱ复合型裂缝端部区域的主应力方程为：

(8)

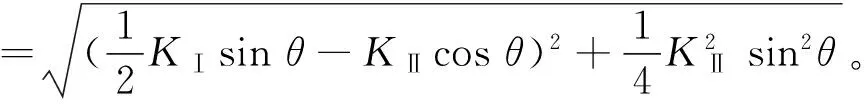
将E0(1-D)εi=σi代入到主应力公式(8)中可以得到：

(9)

根据式(7)和式(9)，计算得到缝尖损伤变化规律的表达式为：

(10)

其中：

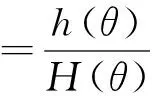
由此，可求得Ⅰ-Ⅱ复合型裂缝的损伤梯度。

图3 G(θ)随扩展角θ变化的规律

裂缝的扩展角即为损伤梯度取极大值时所对应的θ值，由式(10)可知：只需找到G(θ)和g(θ)的极大值就可以找到与之对应的扩展角。根据文献[7]中的试验数据，取α=0.58。通过计算分析可以得到G(θ)-θ对应的关系，如图3所示。最终得到损伤梯度取极大值时所对应的θ值分别为：23°，24°，38°，57°，69°，71°， 81°。

3.2 验证

随着荷载增加，▽D不断变化，裂缝始终沿着其极大值所对应的θ方向扩展。当0°<θ<90°时，上述角度均符合条件，且θ=81°即为裂缝最终的扩展方向，即裂缝的扩展角。根据断裂理论，可以求出最终的开裂角为82°，将两者进行比较，误差为：

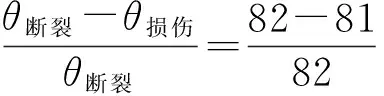
由于经典断裂理论没有考虑材料的初始损伤，所以求得的断裂角偏大。本文采用损伤梯度的方法所得的裂缝扩展角与经典断裂理论所求得的扩展角误差为1.2%(小于3%)，结果较为吻合。

根据Ⅰ-Ⅱ复合型裂缝起裂准则的试验得到裂缝的起裂角平均值为24.52°，与根据损伤得到的裂缝起裂角23°进行对比，两者的相对误差仅为6.1%，小于10%，结果吻合较好，表明应用损伤梯度最大的方法进行裂缝扩展角研究是可行的。

4 结论

(1)本文根据断裂理论计算得到了Ⅰ-Ⅱ复合型裂缝的扩展角表达式及失稳扩展角的数值，将得到的结果与应用损伤理论得到的失稳扩展角进行对比，结果吻合较好。

(2)应用Loland损伤模型，进行Ⅰ-Ⅱ复合型裂缝扩展方向研究，得到的结论是Ⅰ-Ⅱ复合型裂缝扩展方向与缝尖端损伤场的强弱有关。通过缝端损伤场及损伤梯度的计算，分析了Ⅰ-Ⅱ复合型裂缝从起裂至失稳断裂裂缝扩展方向的变化规律，得到了Ⅰ-Ⅱ复合型裂缝的起裂扩展角和失稳扩展角。

(3)将由损伤理论得到的裂缝起裂扩展角与研究混凝土Ⅰ-Ⅱ复合型裂缝起裂准则的试验结果进行了对比，其结果吻合较好，表明应用损伤梯度研究裂缝扩展角是可行的。

[1] 游潇.简析混凝土损伤力学[J].山西建筑,2014,40(8):49-50.

[2]LolandKE.ContinuousDamageModelforLoad-Re-SponseEstimationofConcrete[J].CementandConcreteResearch,1980,10(3):395-402.

[3] 李兆霞.损伤力学及其应用[M].北京:科学出版社,2002:12-20.

[4]KachanovLM.IntroductiontoContinuumDamageMechanics[M].Dordrecht:NijhoffPublishers,1986:97-113.

[5]Sidoroff.DescriptionofAnisotropicDamageApplicationtoElasticity[C]//ProceedingsofIUTAMColloquium.PhysicalNonlinearitiesinStructuralAnalysis.1981:237-244.

[6] 田佳琳,李庆斌.混凝土Ⅰ型裂缝的静力断裂损伤耦合分析[J].水利学报,2007,38(2):205-210.

[7]XuSL,ReinhardtHW.DeterminationofDouble-KCriterionforCrackPropagationinQuasi-brittleFracture,PartⅠ:ExperimentalInvestigationofCrackPropagation[J].InternationalJournalofFracture,1999,98:111-149.

[8] 董伟,何化南,吴智敏,等.光弹贴片法研究混凝土Ⅰ-Ⅱ复合型裂缝扩展过程[J].工程力学,2010,27(9):41-48.

[9] 董伟.混凝土Ⅰ-Ⅱ复合型裂缝起裂准则的试验研究与裂缝扩展过程的数值模拟[D].大连:大连理工大学,2008.

[10] 陈殿华,王向东,邵兵.基于缝端损伤区域的混凝土材料Ⅱ型裂缝扩展角研究[J].河海大学学报:自然科学版,2014,42(3):246-249.

[11] 伍颖.断裂与疲劳[M].武汉:中国地质大学出版社,2008:106-109.

[12] 洪起超.工程断裂力学基础[M].上海:上海交通大学出版社,1997:24-36.

[13] 余天庆,钱济成.损伤理论及其研究[M].北京:国防工业出版社,2001:132-138.

[14] 朱小婷,王向东,吴京,等.基于损伤理论的混凝土构件裂缝的扩展研究[J].三峡大学学报:自然科学版,2014,36(3):75-78.

国家“十一五”科技支撑计划基金项目(2008BAB29B03);国家自然科学基金项目(50878077)

王玉琳(1990-),女,满族,辽宁桓仁人,硕士生;王向东(1965-),女,通信作者，山西运城人，教授,博士,硕士生导师,主要研究方向为工程断裂与损伤.

2015-06-17

1672-6871(2015)06-0051-04

TU528.01

A