深海环境下集体逃逸舱力学特性分析

张 伟，陈 猛，王 政

(河南科技大学 土木工程学院,河南 洛阳 471023)



深海环境下集体逃逸舱力学特性分析

张 伟，陈 猛，王 政

(河南科技大学 土木工程学院,河南 洛阳 471023)

研究了集体逃逸舱耐压结构在深海环境下的力学特性。以新型的变厚度逃逸舱为工程实例，通过有限元计算，分析得到了舱体各不同厚度处的位移、应力分布及其应力最大部位的分布等力学规律。分析结果表明：在静水压力下，舱体的位移以竖向为主，总位移相对较小，刚度满足要求。舱体应力以竖向和切向应力为主，竖向应力以拉应力为主且应力值较大，而切向应力表现为压应力。通过对应力分布规律的分析，所有应力均满足安全要求。

集体逃逸舱；耐压结构；静水压力；位移；应力

0 引言

集体逃逸舱是一种独立的、自成一体的新型脱险装置，应用于深海空间站、潜艇等水下结构，可有效地提高失事水下人员的自救能力，保证脱险过程中人员的安全性，优于过去的任何一种逃生系统[1]。

集体逃逸舱在中国的研究起步较晚，20世纪末才提出了一种通过过渡舱与潜艇对接的可释放的逃逸舱。文献[2]对薄壁球壳耐压体进行了非线性屈曲分析，并对集体逃逸舱的总体结构形式进行了研究。文献[3]通过应用强度稳定综合理论的解析法对深海潜器耐压圆柱壳极限强度进行了分析。文献[4]对集体逃逸舱总体性能进行了研究。文献[5]利用能量法来分析大型圆柱壳体结构的设计,为大型圆柱壳结构的设计提供了重要的参考依据。文献[6]研究了深海载人潜水器耐压球壳，采用接触有限元分析的方法对深海载人耐压球壳的接触问题进行了分析。文献[7-8]分析了带肋圆柱壳结构有限元计算中其强度的影响，并对环肋圆柱壳结构的可靠性进行了计算。文献[9]研究了藕节形切弧连接耐压壳体的强度和稳定性，提出了三藕节切弧连接耐压壳体非线性强度公式和稳定性公式。集体逃逸舱的结构形式是薄壁球壳结构，其主要承压结构是开孔耐压球壳。开孔的存在会产生应力集中,同时也削弱了耐压球壳的极限承载能力[10],为保证开孔球壳的安全性,设计时需要进行强度和稳定性分析。然而，现阶段耐压结构的设计方法依然采用确定性的设计方法，很难将各种不确定性因素影响反映清楚。因此，需要对耐压结构进行进一步可靠性分析，以确定其最危险的失效模式。

本文所研究的集体逃逸舱结构为薄壁耐压球壳，该球壳的变形属于大应变、大变形，考虑应用几何非线性进行计算。本文采用ANSYS软件，对集体逃逸舱在水下静压力作用下的结构强度进行了有限元分析，研究耐压舱体在水下静力作用下舱体各个部位的位移、正应力及其他应力的分布规律，验证了其在水下静压力作用下能够满足安全要求。

1 逃逸舱耐压壳体结构有限元模型建立

1.1 结构材料选取

集体逃逸舱的质量需要严格控制。通过高强度钢和钛合金两种材料的对比分析表明：虽然钛合金的密度比较小，但是钛合金球壳比高强度钢对缺陷更加敏感，从确保安全的角度考虑，选用高强度的980钢作为逃逸舱的材料。980钢：密度ρ=7.85 kg/m3，弹性模量E=2.110 5 MPa，屈服强度σs=785 MPa，泊松比μ=0.3。

1.2 结构模型建立

集体逃逸舱的有限元模型由逃逸舱主体和连接舱体组成，为了减小模型规模，提高计算效率，对结构强度影响较小的部位进行了简化。在ANSYS有限元软件中确立整体坐标系，X轴为径向、Y轴为切向、Z轴为竖向。单元类型采用SHELL93单元，单元需要定义壳体厚度参数，该单元适合于曲壳模型，每个节点都具有6个自由度：沿节点坐标系X、Y、Z方向的平动和沿节点坐标系X、Y、Z轴的转动，变形在两个方向上都是二次的。集体逃逸舱的有限元模型如图1所示。

将耐压体模型的球形壳体和出入口围栏用板单元进行离散，这种板单元具有大变形、塑性功能,能够分析薄壳和中等厚度的壳体,约束了下部出入口围栏的底部节点。出入口围栏的底部与另外的临时连接装置连接,其载荷为均布载荷。经过网格收敛性检查，薄壳处网格尺寸取50 mm×50 mm，其他位置采用30 mm×30 mm。

1.3 模型荷载施加

本文所研究的集体逃逸舱设计水深为1 000 m。静水压力为：

P′=ρgh=1.0 kg/m3×10 N/kg×1 000 m=10 MPa。

根据潜水器规范[11]的要求,计算载荷取对应于1.5倍最大工作深度的压力。因此，文中计算耐压舱体受到的均匀静水压力为:

P=P′×1.5=15 MPa 。

集体逃逸舱承受荷载如图2所示。模型底端采用完全固支的方式进行约束。

图1 集体逃逸舱有限元模型图 图2 集体逃逸舱承受载荷示意图

2 耐压壳体计算结果与分析

本文对集体逃逸舱在水下静压力作用下的结构强度进行了有限元计算，主要从位移、应力等方面分析其不同厚度处的变化规律。

2.1 耐压壳体位移

集体逃逸舱在静水压力作用下，径向、竖向和总位移沿高度的位移值如表1所示。

表1 耐压壳体位移值

从表1可以看出：径向位移值沿高度最大正值为2.10mm，在高度为1.20～1.40m和顶部时出现负值，这两处均为围壁。径向位移最大正值为2.10mm，相对于耐压舱体相应位置处的半径为1.3%;最小值为-1.02mm，相对于耐压舱体相应位置处的半径为0.3%，其相对值均较小。竖向位移沿高度呈增加趋势，在高度为0～1.00m、1.50～2.80m位移的变化较慢，这是由于此处舱体的厚度较大导致的；在舱体顶部位移达到最大，位移绝对值最大为20.00mm，占舱体高度的比例为0.6%，竖向位移相对值较小。总位移大小与竖向位移接近，且变化趋势与竖向位移一致。数值模拟结果显示：耐压舱体的切向位移值基本为0，不考虑其影响，因此，舱体的刚度设计合理。

2.2 耐压壳体正应力

集体逃逸仓在水下静压力作用下，径向、切向、竖向3个方向沿高度的应力值如表2所示。

表2 耐压壳体3个方向应力值

表2表明：在球壳竖向高度1.20～1.60m和2.80～3.06m部位应力值发生了突变，对比耐压舱体的有限元模型图，可知这些部位是围壁的交界处、薄厚球壳交界处、围壁与上围壳交界处、上下围壳交界处等位置，这是因为处于交界处或者壳体厚度变化处，在这些位置出现了应力集中的现象。耐压结构的最大压应力为847.20MPa，最大拉应力为737.43MPa。高强度钢的抗拉抗压强度设计为785MPa。虽然最大压应力大于抗压强度设计值，但是当引入应力因数来验证时，应力因数=最大压应力/抗压强度设计值=1.08，小于规范[11]规定的因数(1.2)，因此耐压壳体满足强度要求。

2.3 耐压壳体的第一、第三主应力和Mises应力

在静水压力作用下，耐压壳体沿高度的第一主应力、第三主应力及Mises应力值如表3所示。

表3 耐压舱体关键部位对应高度的第一主应力、第三主应力及Mises值

表3表明：在静水压力作用下耐压舱体的第一主应力以拉应力为主，局部小范围出现压应力，其最大压应力值较小。在竖向高度为2.60 m时，第一主拉应力值较大，出现应力集中，超过了材料的抗拉强度，这是由于建模时忽略了此处的细部构造导致的，实际耐压舱体在采取一定的构造措施之后应力值会有所降低。在忽略了应力集中处的应力值后，最大主拉应力为604.62 MPa，出现的位置在2.60 m附近，小于高强度钢的抗拉强度值(785 MPa)。

第三主应力在舱体底部应力值较大，呈现出较复杂的变化趋势，且在高度为1.80～2.70 m处应力值接近为0。第三主应力最大值为840.20 MPa，表现为压应力，此值大于高强度钢的抗压强度值(785 MPa)，这是由于施加的荷载为1.5倍实际荷载导致的。因此，不能直接用高强度钢的抗压强度进行校核，其应力因数为1.07，小于规范[11]规定的应力因数，说明抗压舱体的抗压强度符合规范[11]要求。

Mises应力值在舱体底部达到最大值，而后逐渐减小，大约在500 MPa附近波动。Mises应力值最大值为871.11 MPa，此应力值大于高强度钢的屈服强度(785 MPa)，最大拉应力大于抗压强度设计值，但这种现象主要是应力集中的影响，不能直接用高强度钢的抗拉强度进行校核。通过计算应力因数可知：其值为1.08，小于规范[11]规定的因数(1.2)，因此耐压壳体满足强度要求,说明抗压舱体的屈服强度符合规范[11]要求。

表3表明：耐压舱体的强度虽然符合规范[11]要求，但是舱体底部的应力较大，超出了高强度钢的屈服强度，因此须采取相应的构造措施来避免或削弱应力集中的影响，减小此处的应力值。

2.4 耐压壳体强度模拟结果分析

集体逃逸舱作为典型的回转体结构，由耐压球壳和圆柱壳组成，工作时主要承受静水压力。针对此耐压壳体荷载及结构的对称性，文献[1]提出了一种解析单元法计算其强度。对于圆柱壳和球壳这一类在同时承受边界载荷和表面正压力作用下的回转壳，其边界位移和内力关系的表达式的结果形式与由相对应的弹性基础梁推导的结果是一致的。解析单元法是在回转体上选择夹角为dθ的两个纬线剖面内的单元体进行受力分析，可得到回转体平衡方程为：

其中：T、N、M分别为所选单元体上所受拉力、剪力和弯矩；ρ为球壳曲率；p为正压力。

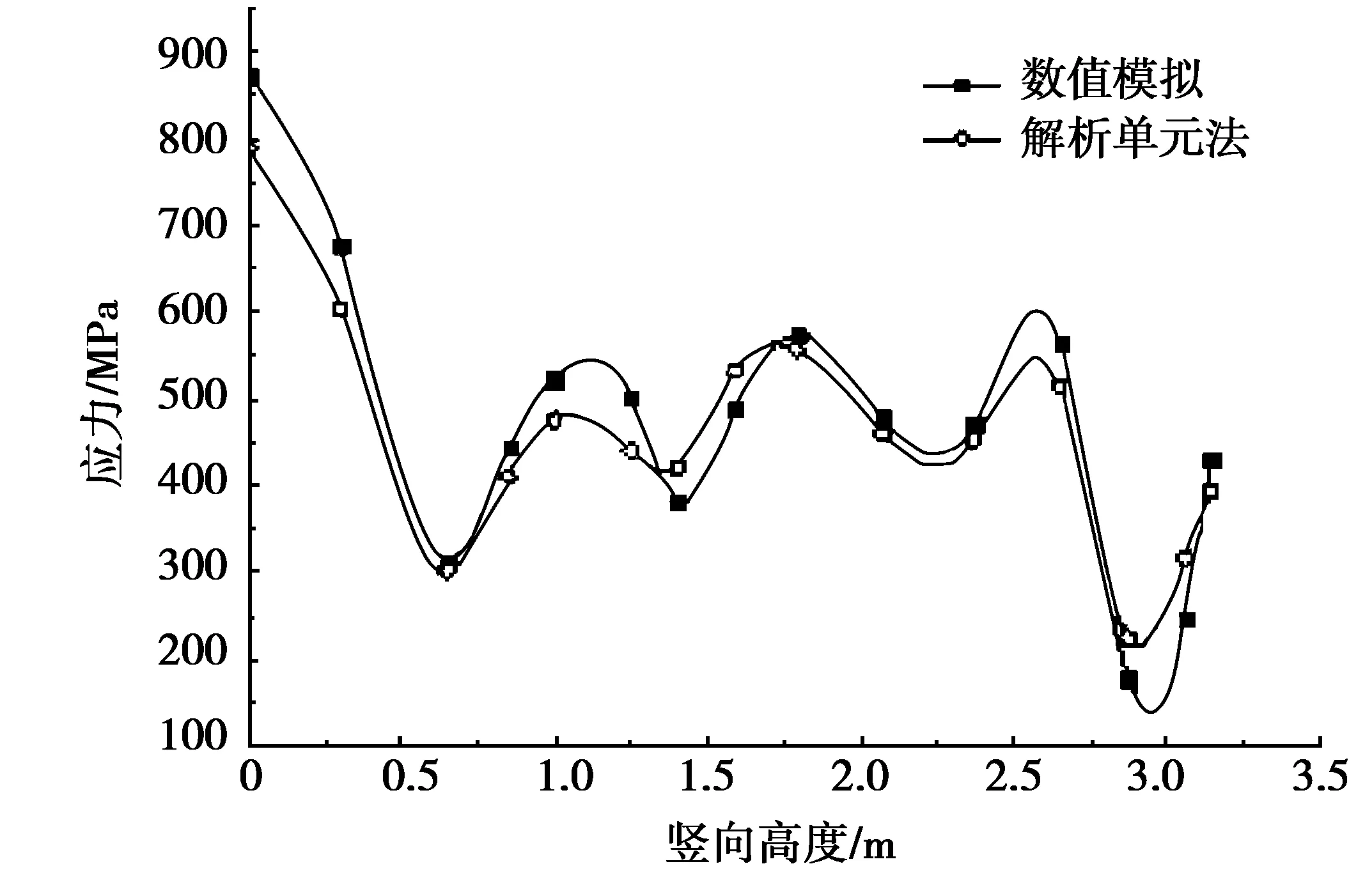
图3 耐压舱体沿竖向高度应力分布曲线

将数值模拟的Mises应力计算结果与解析单元法的计算结果比较，如图3所示。

由图3可见：模拟数据和解析单元法计算数值结果比较吻合，相对误差低于10%。从趋势来说解析单元法计算出的应力值较小，这主要是因为数值模拟中一些部位存在应力集中的现象。通过和解析单元法的对比，从理论上验证了ANSYS数值模拟结果的正确性。

3 结论

(1)耐压舱体的径向和环向位移均较小，以竖向位移为主，竖向位移沿舱体高度呈增加趋势，在舱体顶部达到最大值，最大值占舱体高度的比例较小，耐压舱体的刚度设计合理。

(2)竖向和径向的正压力在舱体厚度变化处虽然出现了局部应力集中，但考虑到建模时对局部的简化处理可以不予考虑，竖向和环向整体应力均小于高强度钢的抗拉抗压强度及规范规定的应力因数。切向应力在舱体底部的应力虽然略大于高强度钢的抗压强度，但小于规范[11]规定的应力因数。抗压舱体的强度符合要求。

(3)抗压舱体的第一、第三主应力及Mises应力值的变化规律较为复杂，第一主应力值相对于第三主应力值及Mises值较小。第三主应力值及Mises值在舱体底部达到最大值，应力值均略大于所用材料的屈服强度，但小于规范[11]规定的应力因数，抗压舱体的强度设计符合要求。

(4)通过ANSYS模拟数据与解析单元法的结果对比可知：耐压舱体沿竖向高度应力分布趋势一致，从而验证了数值模拟结果的正确性。

[1] 余俊.深海空间站集体逃逸舱技术研究[D].上海:中国船舶科学研究中心,2013.

[2] 黄浩才.集体逃生舱总体结构形式研究[D].武汉:武汉理工大学,2006.

[3] 冯亮,佟福山.基于强度稳定综合理论的深海潜器耐压圆柱壳极限强度的解算[J].哈尔滨工程大学学报:自然科学版,2012,33(2):150-154.

[4] 刘明静.集体逃逸舱总体性能研究[D].武汉:武汉理工大学,2006.

[5] 杨民献,张淑芬,王彦生.圆柱壳的屈曲荷载最大化设计[J].河南科技大学学报:自然科学版,2003,24(1):71-74.

[6] Li X Y,Cui W C.Contact Finite Element Analysis of a Spherical Hull in the Deep Manned Submersible[J].Journal of Ship Mechanics,2004,8(6):85-94.

[7] 刘小宛，梁斌.球肋圆柱壳的自由振动特性[J].河南科技大学学报:自然科学版,2014，35(2)：62-66.

[8]Yu Y X,Liu F J,Zhang W.Improving of RSM-FORM and Application to Reliability Calculation of Ring-stiffened Cylindrical Shell[J].Journal of Ship Mechanics,2012,16(3)：271-276.

[9] 伍莉,陈爱志,陈小宁.藕节形大深度潜水器耐压壳体强度与稳定性研究[J].船舶力学,2010,14(1/2):74-83.

[10] 余俊,王永军,潘广善.集体逃逸舱开孔耐压球壳优化设计[J].舰船科学技术,2014,36(1):104-110.

[11] 中国船级社.潜水系统和潜水器入级与建造规范[S].北京:人民交通出版社,1996.

国家自然科学基金项目(51208182)

张伟(1966-),男,河南汝州人,教授,博士后,硕士生导师,研究方向为结构强度和可靠性评估.

2015-01-04

1672-6871(2015)06-0026-04

U662.3

A