倒排索引中的文档序号重排技术综述

2015-04-21刘欣然

中文信息学报 2015年2期

关键词：重排复杂度序号

史亮，张鸿，刘欣然，王勇，王斌

(1. 国家计算机网络应急技术处理协调中心，北京 100029； 2. 中国科学院信息工程研究所，北京 100093)

倒排索引中的文档序号重排技术综述

史亮1，张鸿1，刘欣然1，王勇1，王斌2

(1. 国家计算机网络应急技术处理协调中心，北京 100029； 2. 中国科学院信息工程研究所，北京 100093)

倒排索引作为文本搜索的核心索引技术，广泛应用于搜索引擎、桌面搜索和数字图书馆领域。倒排索引由字典和对应的倒排表组成，倒排表一般采用差值存储和整数编码进行压缩。研究表明，当倒排表具有较好的局部连续性时，上述方法能够获得很高的压缩率。整数编码研究通过不断改进编码算法来充分利用倒排表的局部连续性特征，而文档序号重排正是一种对文档序号重新排列来产生局部连续性的技术。通过文档序号重排，索引压缩率得到显著提高。该文主要介绍近年来文档序号重排技术取得的研究成果：首先介绍索引压缩的基本原理，然后详细介绍文档序号重排技术，包括分析、对比各个方法的优劣；最后对文档序号重排技术进行总结、整理和展望。

搜索引擎；性能优化；索引压缩；文档序号重排；局部连续性

1 引言

随着互联网的快速发展，搜索引擎已经成为人们获取信息的主要手段。在搜索引擎中，倒排索引被证明是最合适并广泛使用的索引格式[1]。随着网络数据和用户规模的不断增长[2-3]，索引存储和查询处理都面临前所未有的挑战。

根据倒排索引的特点，索引压缩(Index Compression)采用文档序号重排技术和整数编码算法对倒排索引进行压缩。通过索引压缩，可以把倒排索引的体积压缩到原始文档集合的15%～25%左右。索引压缩的优势主要体现在以下方面： 1)减少倒排索引占用的磁盘空间，节约存储成本；2)通过压缩，降低了索引从磁盘传输至内存过程中的延迟，提高了查询处理效率；3)在有限容量的缓存中存储更多的索引，提高查询处理过程中的缓存命中率[4]。

本文的目标是介绍索引压缩中文档序号重排技术的研究进展。文档序号重排是索引压缩的一项重要技术。研究表明，倒排表中的局部连续性(局部连续性是指具有连续文档序号的文档在倒排表中多次连续出现)能够有效地提高索引压缩率。

倒排索引一般由字典和倒排表组成，和倒排表相比，字典只占非常小的空间，所以如果不做特别说明，索引压缩一般是指倒排表的压缩。倒排表采用差值存储，然后使用整数编码算法进行压缩。整数

编码算法主要是在不改变初始文档序号分布的前提下，通过改进算法提高索引压缩率。目前主流的编码算法已经能够兼顾压缩、解压速度和压缩率，并且可以根据实际需求选择相应的编码算法。但是受限于文档序号的初始分布，倒排表中的局部连续性往往较差，仅通过优化编码算法来提高索引压缩率的空间已经不是很大。

文档序号重排是一种对倒排索引中文档序号重新分配的技术。相比于初始文档序号分布，重排后的文档序号具有更好的局部连续性，进一步提高了索引压缩率。该方法提出后，在搜索引擎中得到了广泛应用，在研究人员的努力下，其可用性和扩展性都得到了有效的改进。

本文的组织结构如下：第2节介绍了索引压缩的基本原理，第3节介绍了文档序号重排技术的基本原理和方法，第4、5、6节从三个类别整理和总结了近年来文档序号重排技术的研究工作，第7节对本文进行了总结和展望。

2 索引压缩

倒排表的基本形式如式(1)所示：

(1)

词项ti通过文档分词得到，存放在字典中，倒排表存放出现该词项的文档个数fti和长度为fti的文档序号记录表，这里暂不考虑词项ti在每个文档中出现的频率和位置信息。

观察发现，如果把倒排表中的文档序号升序排列，然后仅存储文档序号之间的差值(简称d-gap)，可以有效减少存储倒排表所需空间。这是因为d-gap要远小于原始文档序号，尤其随着文档数目的增长文档序号越来越大时更是如此。更小的数值意味着可以采用更短的编码表示，所以在实际系统中文档序号往往采用d-gap表示，又称倒排表的d-gap形式，如式(2)所示。

(2)

对d-gap压缩，本质上是对整数进行压缩。所以当把倒排表按照d-gap形式存储后，便可以采用整数编码算法作进一步处理。按照码长是否可变，整数编码可以分为定长编码和变长编码。定长编码是指每个整数由固定长度的码字表示，如INT32、INT64等。变长编码会根据整数的大小，选择不同的码长。变长编码又分为变长比特编码和变长字节编码。变长比特编码包括Gamma编码[5]、Delta编码[5]、Rice编码[6]、Simpe9编码[7]、PForDelta编码[8]、IPC编码[9]等，特点是在比特粒度上长度可变；变长字节编码主要指VByte编码[10]，特点是在字节粒度上长度可变。相比于变长字节编码，变长比特编码的优点是能够获得更高的压缩率，但是编码和解码过程都需要大量计算，速度更慢。

举例来说，假如要对1 000篇文档建立倒排索引，其中词项t在4篇文档中出现，文档序号分别是200、407、412和855，文档序号采用Gamma编码。表1将倒排表的基本形式和d-gap形式进行了对比，包括存储方式和所需的编码长度。

表1 倒排表的基本形式和d-gap形式所需编码长度对比

整数X的Gamma编码需要(2×log2X+1)比特，所以表1中倒排表基本形式共需要68比特，d-gap形式共需要52比特。从这个简单的例子可以看出，使用差值存储，d-gap形式总共节约了16比特。在实际的倒排索引中，d-gap形式带来的好处更加明显。

3 文档序号重排技术

倒排表具有较好的局部连续性时，差值存储能够获得更高的压缩率，这是因为好的局部连续性意味着倒排表中存在更多数值较小的d-gap。通过前面的介绍可以知道，更小的数值可以采用更短的编码表示。但在实际情况中，受限于文档序号的分布，倒排表的局部连续性往往不是很好。

近年来，研究人员提出了文档序号重排技术(DocumentIdentifierReassignment)，按照文档之间的相似度，对文档序号重新分配。经过文档重排，显著提高了倒排表的局部连续性。实验表明，文档序号重排技术不仅提高了索引压缩率[11]，而且优化了查询处理的性能[12]。此外，通过对文档序号进行重排，还能够更好地管理新加入的文档[13]。

(3)

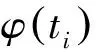
以表1中的倒排表为例，对其进行文档序号重排后得到的倒排表及其d-gap形式如表2所示，采用Gamma编码。在本例中，通过将原始的文档序号200,407,421,855映射到10,13,14,和201，编码长度由原来的52比特减少为26比特。

表2的例子简单演示了文档序号重排技术对单个倒排表的影响。实际情况中，对单个倒排表中的文档序号重排将会影响全局的d-gap分布，所以文档序号重排的过程是一个求全局最优解的过程。

表2 倒排索引的基本形式和重排后d-gap形式编码长度对比

最简单的文档序号重排方法是对所有N篇文档序号进行全排列，然后找出使总的编码长度之和最小的排列，时间复杂度为O(N!)。该方法能够有效解决文档序号重排问题，但仅适用于小规模数据集。RoiBlanco等人指出[14]，该问题的求解类似于PSP(PatternSequencingProblems，模式序列问题)，属于NP(Non-deterministicPolynomial，非确定性多项式)问题，暂无确定性解法，只能通过近似的方法求解。

目前解决该问题的基本做法是将连续的文档序号分配给相似文档，这样做是因为相似度高的文档在倒排表中的共现频率也高，可以产生很好的局部连续性，增加倒排表中小的d-gap出现的频率。

所以文档序号重排问题可以分为三个子问题： 1)如何定义文档相似度；2)如何寻找相似文档；3)如何重新分配文档序号。其中第二个子问题可以认为是最核心的问题。

本文根据寻找相似文档方法的不同，把相关工作分为三类并分成三节进行详细介绍。第4节主要介绍基于聚类的方法，第5节介绍基于TSP(TravelingSalesmanProblem，旅行商问题)的方法，第6节介绍基于排序的方法。

4 基于聚类的方法

基于聚类方法的特点是通过对文档集合进行聚类，寻找相似文档。根据聚类算法的区别，可以分为自顶向下和自底向上的方法。

4.1 自顶向下的方法

自顶向下的方法主要包括B&B、TransactionalB&B和Bisecting算法，这些算法的基本思想是将原始文档集合看成一个整体，然后自顶向下递归地对文档集合进行聚类，每一次聚类将相似文档划分到一个类别中。聚类的同时伴随着调整类别之间先后顺序的过程。

(1)B&B算法

Blandford和Blelloch(以下简称B&B)第一次提出利用聚类算法对文档序号进行重新排列的方法，算法的基本步骤如下(预先已对文档集合建立倒排索引)。

1) 选择中心点：首先对给定的文档集合进行抽样，忽略文档中的高频词，根据文档之间的余弦相似度计算得到DSG(DocumentSimilarityGraph，文档相似图)，然后调用Metis[16]图切分算法将DSG划分为两个子集，这两个子集的中心向量作为新的聚类中心；

2) 划分剩余文档: 剩余未被抽样选中的文档，根据到两个聚类中心的余弦相似度，划分到相应的文档集合中；

3) 文档集合排序：对两个子集进行排序；假设将文档集合S划分为子集I1和I2，令IL为节点S左祖先的左孩子节点，IR为节点S右祖先节点的右孩子节点。之所以要对子集I1和I2排序，是因为需要考虑I1、I2和其前驱文档集合IL及后继文档集合IR的相似度，通过排序，可以将相似度更高的文档集合放在一起；

4) 递归聚类：递归调用上述过程，直到每个文档子集合只包含单个文档为止。

通过对文档集合自顶向下递归聚类得到一个层次聚类树，树的叶子节点是单个文档，然后从左至右遍历树中所有的叶子节点，最后按照遍历的次序对文档分配新的文档序号。

对文档抽样处理，可以降低DSG的规模，减少算法执行的时间；忽略高频词是因为高频词对应倒排表的d-gap已经较小，通过文档序号重排所得提升有限，相比整体优化效果可以忽略不计，而且高频词的存在影响了文档相似度的计算。

(2)TransactionalB&B算法

B&B算法在对文档序号进行重排之前，需要预先对文档建立倒排索引，增加了算法的额外开销。TransactionalB&B[16]算法对B&B算法进行了改进，跳过了建立倒排索引的步骤，并且在中心点选择和文档集合排序上进行了改进，其基本步骤如下：

1) 选择中心点：类似于B&B算法，但是在计算DSG时使用Jaccard相似度；因为没有预先建立倒排索引，所以没有过滤高频词；

2) 划分剩余文档：根据Jaccard相似度划分未被抽样选中的剩余文档；

3) 递归聚类：和B&B算法不同，该方法先进行递归划分至叶节点，然后对文档集合排序。这样做的结果是先得到一个层次聚类树，然后再自底向上对文档集合排序；

4) 文档集合排序：假设对文档子集I1和I2排序，如果I1中最后一个文档和I2中第一个文档的Jaccard相似度大于I1中第一个文档和I2中最后一个文档的相似度，则将保持I1和I2的次序(I1在I2之前)，否则交换两者次序。

最后从左至右遍历层次聚类树的叶子节点，为每个文档分配新的文档序号。

(3)Bisecting算法

Bisecting[16]方法在TransactionalB&B算法的基础上，进行了进一步简化。在选择中心点时，随机地挑选两个文档作为聚类中心，而不像B&B和TransactionalB&B方法一样，使用图切分算法选择聚类中心，从而省去了计算DSG和图切分的步骤，降低了算法的复杂度。当然，这样做牺牲了聚类的准确性，影响了文档序号重排后最终的索引压缩效果。

4.2 自底向上的方法

不同于自顶向下划分文档集集合进行聚类的方法，自底向上的方法从原始文档集合开始，根据文档与聚类中心的相似度，依次将每个文档划分到距离最近的类别中，最后得到k个文档聚类。自底向上的方法主要包括k-means-like算法和k-scan算法。

(1)k-means-like算法

基本的k-means算法是从文档集合中选出k个聚类中心点，然后将剩余文档按照到各个聚类中心点的距离，聚到距离最近的类别。待所有文档分配完成后，重新计算k个聚类的中心点，然后重复上述步骤，直到k个中心点不再变化或者达到给定的收敛条件为止。

k-means算法由于复杂度的原因，在文档序号重排问题中并不适用。Silvestri在文献[16]中提出了一个轻量级的k-means-like聚类算法，该算法在k-means算法的基础上进行了简化，只进行一次中心点选择和文档划分。算法的具体步骤如下：

1) 选择中心点：使用Buckshot[17]方法，选取k个聚类中心点；

2) 划分剩余文档：根据Jaccard相似度，将剩余文档分配到k个类别中；

(2)k-scan算法

k-scan[16, 18]算法是另一种轻量级聚类算法，假设对N篇文档进行序号重排，共有k个类别，具体步骤如下。

1) 文档预排序：对N篇文档，按照文档长度降序排列；

2) 选择中心点：每次选择剩余文档集合中长度最长的文档作为聚类中心；

3) 划分剩余文档：根据Jaccard相似度，从剩余文档集合中选择(N/k-1)个和聚类中心相似度最高的文档添加到该类别；

4) 重复第2)、3)步k次，得到k个文档聚类，每个类别中包含N/k个文档。

在k-means-like算法和k-scan算法运行完成后，得到k个文档类别，最后根据k个中心点产生的顺序和以及每个类别里文档被添加的顺序，给文档分配新的序号。

4.3 方法小结

本节介绍的方法主要是通过聚类算法，将文档集合中相似度比较高的文档添加到同一个类别中，然后给同一个类别中的文档分配连续的文档序号，同时也考虑了类别之间的相似度。基于聚类方法的优点是能够有效地在倒排表中产生局部连续性，提高了索引压缩率；缺点是算法复杂度较高，B&B算法构建、划分DSG的空间和时间复杂度均为O(m2)，其中m为抽样集合的大小；建立层次聚类树的空间、时间复杂度为O(nlogn)。其他基于聚类的算法和B&B相比，在时间复杂度和空间复杂度上进行了优化，但均以牺牲聚类的准确性为代价，最后实际的压缩效果也差一些。

5 基于TSP的方法

TSP又称旅行商问题，是一个最优化问题：有n个城市，一个旅行商要从某一个城市出发，走遍所有的城市仅且一次，再回到他出发的城市，求最短路线。相关研究工作利用了TSP的思想来求解文档序号重排问题。

5.1 基本的TSP的方法

Shieh等人首次提出了文档序号重排问题转化为TSP问题进行求解[19]。根据前面介绍，文档序号重排过程就是寻找文档集合中相似文档的过程，如果把DSG中边的权重定义为文档之间的相似度，则文档重排可以看作从一个文档开始，遍历所有的文档仅且一次，再回到开始文档，求相似度之和最大的路径。找到这样的路径后，再按照路径中文档节点遍历的顺序，重新分配序号。在这里，相似度定义为两个文档之间共现词项的个数。

TSP被证明是NP问题，Shieh等人分别采用了贪心算法和生成树算法求解。贪心算法又包括Greedy-NN(NearestNeighbor)和Greedy-NA(NearestAddition)方法。Greedy-NN算法挑选路径中下一个节点的策略是每次都选择和当前路径的最后一个节点相似度最大的节点，而Greedy-NA算法选择下一个节点的策略是计算剩余节点和当前路径上所有节点的相似度，然后选择相似度最大的节点加入到当前路径的末端。

生成树算法的思路是首先找到DSG的一棵最大生成树，然后使用广度优先(BFS)或者深度优先(DFS)遍历生成树，得到遍历所有文档的一条路径，然后依据路径中节点出现的顺序重新分配文档序号。具体的最大生成树算法可以采用Kruskal算法和Prim算法。

实验结果表明，采用Greedy-NN算法进行文档序号重排后的实验结果要好于Greedy-NA算法和生成树算法，也要优于前面介绍的基于聚类的算法，但是该算法的缺点是时间复杂度和空间复杂度太高，不适合在大数据集上使用。

5.2 结合SVD的TSP方法

上述TSP算法的基本思想是从DSG中寻找最优路径，所以必须保存DSG，而随着文档数量的增长，DSG所需的存储空间急剧膨胀，于是RioBlanco等人提出了利用SVD(SingularValueDecomposition，奇异值分解)对DSG进行降维的方法[20, 21]。

假设有一个t×d维词项-文档矩阵X，其中t代表词项，d代表文档。对该矩阵进行SVD分解，可以得到三个子矩阵，如式(4)所示。

(4)

(5)

则d×d维文档-文档矩阵DSG可以表示为式(6)。

(6)

(7)

经过SVD分解后，文档之间的相似度可以通过矩阵D和S计算得到，所以只需要保存d×k维的矩阵D和对角矩阵S的k个对角线元素即可，而不需要保存完整的d×d维文档-文档矩阵DSG。根据实际应用的需求，k值可以取几十到几百，显著降低了算法的空间复杂度。

另一个关于时间复杂度的优化是把原始文档集合分为c块，在每一块内使用SVD+TSP，块与块之间的次序可以通过从每个块中选取一个文档，然后使用Greedy-NN算法决定。

实验结果表明，当k=200时，可以在时间和文档序号重排效果之间达到较好的平衡点。采用分块的策略时，c=1表示不分块，随着c值增加，程序运行时间减少，序号重排后的压缩效果也逐渐变差，可以根据实际需求选择参数。

结合SVD的TSP方法通过降维和分块，显著降低了TSP求解的空间复杂度和时间复杂度，但是另一方面，由于SVD分解本身就是一项时间复杂度较高的步骤，所以总的来说，该方法适用范围有限，在小规模的文档集合上使用比较合适。

5.3 结合LSH的TSP方法

为了将基于TSP的文档序号重排方法扩展到大规模数据集，Ding等人提出了结合LSH(LocalitySensitiveHash，局部敏感哈希)的TSP方法[22]，该方法基本思路是通过抽样对原始的DSG进行简化，每个节点仅保留k条邻近边(k≪n)，即每个节点仅保留k个邻居节点，在抽样得到的稀疏图上求解TSP。主要步骤如下：

1) 词项抽样：扫描文档集，使用Min-Hash[23]算法从每个文档中选取s个词项(s可以任意取值，这里设为100)；

2) 选择最邻近候选文档：使用LSH[24-25]算法为每个节点挑选k′>k个邻近节点；

3) 过滤候选文档：计算每个节点和选出的k′个候选文档的相似度，仅保留k个相似度最高的文档；

4) 求解TSP：使用Greedy-NN算法求解相似度之和最大的路径。如果出现某个节点的k个邻近节点都已在路径中，导致无路可走的情况，则选择剩余图中权重最大的边，将对应节点加入路径。

在计算两个文档di，dj相似度时，Ding等人实验了多种方法，如表3所示。其中n为文档个数，ft为词项频率。

表3 结合LSH的TSP方法使用的相似度计算方法

除了上面介绍的四种方法，Ding还提出，使用Greedy-NN求解TSP时，每一步都选择和当前路径的尾节点相似最高的文档，这样做的目的是最大化倒排表中1-gap的数目，但是却忽略了其他数值的d-gap。

为了考虑其他数值d-gap的影响，定义词项t对应的倒排表中j-gap的权重为：如果j

如图1所示，假设候选文档是有D1和D2，假设文档D1包含词项a和c，文档D2包含词项a、b和d，所以文档D1对应的d-gap权重之和为a、c对应的倒排表中3-gap和4-gap的权重之和；文档D2对应的d-gap权重之和为词项a、b和d对应的倒排表中3-gap、5-gap和1-gap的权重之和。最后选择权重之和最大的文档作为路径中的下一个节点。

图1 文档d-gap权重的计算(a, b, c, d表示词项，横线上的数字表示d-gap的数值)

实验结果表明，结合LSH的方法可以有效地处理大规模数据，并且得到较好的压缩效果。同时，在进行候选文档选取时，考虑文档d-gap权重影响的方法，其压缩率要高于通过其他四种相似度选取候选文档的方法。

5.4 方法小结

基于TSP的文档序号重排技术被认为是目前比较好的方法，对索引压缩率的提高也最明显。基本的TSP方法，其时间复杂度和空间复杂度均为O(n2)，性能最差，不太适合大规模数据，SVD方法通过矩阵分解将算法的空间复杂度降低到O(nk)(其中k为需要保留的矩阵维度)，但是时间复杂度没有得到优化。LSH方法通过局部敏感哈希将算法的空间和时间复杂度降低到O(nk)(其中k为抽样的文档数)，使TSP算法能够很好地处理大规模数据集，但是抽样造成了精度损失，影响了最后的压缩效果。

6 基于排序的方法

前面介绍的文档序号重排方法，包括基于聚类的方法和基于TSP的方法，都是通过计算文档之间相似度，然后寻找近邻文档，虽然通过降维或者抽样可以降低整个过程的空间复杂度和时间复杂度，但是在大规模数据下，由于聚类、TSP本身的复杂性，算法实用性仍有一定限制。下面要介绍的算法采用排序的策略挖掘文档之间的相似性，其时间复杂度和空间复杂度相比于前面介绍的方法，都得到了进一步降低。

6.1 基于URL排序(URLSORT)的方法

Silvestri提出了基于URL(UniformResourceLocator，统一资源定位器)字典序排序的文档序号重排方法[26]。这样做的依据是URL一般都有层次目录结构，内容相似的文档往往会被人为存放在名称相同或者相似的目录下。利用这个特征，在Web数据集上可以对每个文档对应的URL按照字典序排序，然后按照这个顺序对分配新的文档序号。

实验表明，通过该方法进行文档序号重排的结果和基于聚类的方法的结果相当，而在时间和空间复杂度上，都得到了显著的优化。由于依赖于文档的URL，该方法在桌面搜索、图书搜索等领域有一定的局限性。

6.2 基于词项排序(TERMSORT)的方法

Shi等人在文献[27]中提出了基于词项对文档进行排序的方法，然后按照排序后的文档次序，重新分配文档序号。该方法的基本依据是如果两篇文档相似，那么其中包含的词项重复的可能也比较大。如果按照词项是否出现，对文档进行排序，那么相似的文档由于包含重复的词项，排序后邻近的概率会比较高。该方法就是使用基于排序的方式来挖掘文档集合中的相似文档。具体的步骤为：

1) 选择对文档排序时，词项的比较顺序：作者在文中实验了三种顺序，分别是文档频率升序、降序和原始顺序；

2) 按照第1)步确定的词项顺序，对文档降序排列：文档大小的判断的依据是如果文档A包含词项t而文档B不包含，则文档A> 文档B；

3) 按照排序后的文档，重新分配文档序号。

实验结果表明，当词项按照文档频率降序排列时，该方法能够获得最好的结果，其索引压缩率和基于TSP的方法基本持平，但是算法复杂度明显优于基于TSP的方法。

6.3 方法小结

本节介绍的方法通过排序寻找文档集中的相似文档，进而在倒排表中产生局部连续性。因为不需要计算文档集合中两两文档之间的相似度，基于排序的方法其算法复杂度要好于前面介绍的方法。基于URL的方法由于依赖于文档的URL属性，应用范围具有一定的局限性。基于词项排序的方法依赖于预先对词项按照文档频率排序，所以在重排之前需要对文档集合进行预处理，得到相应的词项信息。

7 总结

本文总结了目前常见的文档序号重排方法。当倒排表采用差值存储并使用整数编码进行压缩时，通过对文档序号进行重排，可以有效地在倒排表中产生局部连续性，显著提高索引压缩率。

表4概括和总结了本文介绍的文档序号重排方法，包括每种方法的步骤、时间复杂度和空间复杂度。

这里需要注意的是，在基于聚类的方法和基于TSP的方法中，为了表示方便，我们把计算两个文档相似度的时间复杂度作为常数时间O(1)，但在实际情况中计算文档相似度需要对两个文档中的词项进行遍历，时间复杂度正比于文档的长度，所以准确的表示应该把表格中的时间复杂度再乘以文档长度。同样，在表示空间复杂度时，我们忽略了文档的长度，将一个文档所需空间看作O(1)。而在基于排序的方法中，我们将比较两个URL的时间复杂度看作是常数时间O(1)，在计算其空间复杂度时，将一个URL占用空间看作是O(1)。

总的来说，基于TSP的文档序号重排技术被认为是目前比较好的方法，对索引压缩率的提高也最明显，但是性能最差，不太适合大规模数据，虽然可以通过优化进一步降低算法复杂度，但是以牺牲压缩率为代价；基于聚类的方法算法复杂度低于基于TSP的方法，适用于各种规模的数据集，但是其压缩效果比较差。这两类文档序号重排方法均需要计算文档之间相似度，而基于排序的方法通过比较寻找相似文档，算法性能优于前两类方法，压缩效果也比较好，在数据规模上没有限制，具有良好的可扩展性。

在实际应用中，可以根据软硬件环境、文档规模和压缩率的要求，选择合适的方法。

此外，从表4可以看出，我们可以综合现有的文档序号重排的方法，比如将基于聚类的方法和SVD分解结合[21]，或者将聚类和排序的方法结合[28]，也都获得了很好的实验结果。

文档序号重排技术仍存在很多开放性问题，比如目前的方法主要是通过寻找相似文档，然后分配连续文档序号的方法。总而言之，这些方法都是通过间接的方法来优化d-gap分布。是否存在一个根据倒排表中的文档特征，直接以最小化d-gap编码长度的文档序号重排方法，是我们下一步要研究的问题。

表4 文档序号重排方法汇总

[1] Witten I H, A Moffat, T C Bell. Managing Gigabytes: Compressing and Indexing Documents and Images[M]. Morgan Kaufmann, 1999.

[2] IDC. Digital Universe Study[OL]. 2011. http://idc-docserv.com/1142.

[3] CNNIC. 第28次中国互联网络发展状况统计报告[OL]. 2012. http://www.cnnic.net.cn/dtygg/dtgg/201107/W020110719521725234632.pdf.

[4] Scholer F, et al. Compression of inverted indexes for fast query evaluation[C]//Proceedings of the SIGIR’05. Tampere, Finland: ACM, 2002: 222-229.

[5] Elias P. Universal codeword sets and representations of the integers[J]. IEEE Transactions on Information Theory, 1975, 21(2): 194-203.

[6] Rice R, J Plaunt. Adaptive variable-length coding for efficient compression of spacecraft television data[J]. IEEE Transactions on Communication Technology, 1971, 19(6): 889-897.

[7] Anh V N, A Moffat. Inverted index compression using word-aligned binary codes[J]. Inf. Retr., 2005, 8(1): 151-166.

[8] Zukowski M, et al. Super-scalar RAM-CPU cache compression[C]//Proceedings of the ICDE’06. 2006: 59.

[9] Moffat A, L Stuiver. Binary interpolative coding for effective index compression[J]. Inf. Retr., 2000, 3(1): 25-47.

[10] Williams H E, J Zobel. Compressing integers for fast file access[J]. Computer Journal, 1999, 42(3): 193-201.

[11] Yan H, S Ding, T Suel. Inverted index compression and query processing with optimized document ordering[C]//Proceedings of the WWW’09. Madrid, Spain, 2009: 401-410.

[12] Manning C D, P Raghavan, H Schutze. Introduction to Information Retrieval[M]. Cambridge University Press, 2008.

[13] Zobel J, A Moffat. Inverted files for text search engines[J]. ACM Computing Surveys, 2006,38(2):6.

[14] Blanco R, A Barreiro. Characterization of a simple case of the reassignment of document identifiers as a pattern sequencing problem[C]//Proceedings of the SIGIR’05. Salvador, Brazil, 2005: 587-588.

[15] Karypis G, V Kumar. A fast and high quality multilevel scheme for partitioning irregular graphs[J]. SIAM Journal on Scientific Computing, 1998, 20(1): 359-392.

[16] Silvestri F, S Orlando, R Perego. Assigning identifiers to documents to enhance the clustering property of fulltext indexes[C]//Proceedings of the SIGIR’04. Sheffield, United Kingdom, 2004: 305-312.

[17] Cutting D R, et al. Scatter/gather: A cluster-based approach to browsing large document collections[C]//Proceedings of the SIGIR’92. 1992: 318-329.

[18] Silvestri F, R Perego, S Orlando. Assigning document identifiers to enhance compressibility of Web Search Engines indexes[C]//Proceedings of the SAC’04. Nicosia, Cyprus, 2004: 600-605.

[19] Shieh W Y, et al. Inverted file compression through document identifier reassignment[J]. Inf. Process. Manage., 2003, 39(1): 117-131.

[20] Blanco R,Barreiro. Document identifier reassignment through dimensionality reduction[J]. Advances in Information Retrieval, 2005: 375-387.

[21] Blanco R, A. Barreiro. TSP and cluster-based solutions to the reassignment of document identifiers[J]. Inf. Retr., 2006. 9(4): 499-517.

[22] Ding S, J Attenberg, T Suel. Scalable techniques for document identifier assignment in inverted indexes[C]//Proceedings of the WWW’10. Raleigh, North Carolina, USA, 2010: 311-320.

[23] Broder A Z, et al. Min-wise independent permutations[C]//Proceedings of the STOC’98. 1998:327-336.

[24] Haveliwala T, A Gionis, P Indyk. Scalable techniques for clustering the web[C]//Proceedings of the Third International Workshop on the Web and Databases. Dallas, Texas, 2000.

[25] Indyk P, R Motwani. Approximate nearest neighbors: towards removing the curse of dimensionality[C]//Proceedings of the STOC’98. 1998: 604-613.

[26] F Silvestri. Sorting out the document identifier assignment problem[C]//Proceedings of the ECIR’07. Rome, Italy, 2007: 101-112.

[27] Shi L, Wang B. Yet Another Sorting-Based Solution to the Reassignment of Document Identifiers[M]//Information Retrieval Technology. Springer Berlin Heidelberg, 2012: 238-249.

[28] Chen C, et al. Optimize document identifier assignment for inverted index compression[J]. Journal of Computational Information Systems 6, 2010: 339-346.

[29] Dan B, Guy B. Index compression through document reordering[C]//Proceedings of the DCC’02. IEEE Computer Society, 2002: 342.

Reassignment of Document Identifiers in Index Compression

SHI Liang1, ZHANG Hong1, LIU Xinran1, WANG Yong1, WANG Bin2

(1. National Computer Network Emergency Response Fechnical Team/Coordination Center of China, Bejing 100029, China; 2. Institute of Information Engineering, Chinese Academy of Sciences, Beijing 100093, China)

The inverted index has been widely used as the core data structure in search engine, desktop search and digital library. by. To best compress it via the d-gap or the integer coding, the algorithm called Document Identifiers Reassignment is usually adopted to achieve a high locality in an inverted index. This paper first introduces the basic principle of index compression, and then focuses on state-of-the-art techniques on document identifiers reassignment with an analysis of the pros and cons. It also summarizes all the related work and discusses the future work of document identifiers reassignment.

search engine; performance optimization; index compression; document identifier reordering; locality