煤矿区应急救援站多目标选址决策
2015-04-21王亚阳王汉斌
王亚阳,王汉斌
(太原理工大学经济管理学院,山西 太原 030024)
煤矿区应急救援站多目标选址决策
王亚阳,王汉斌
(太原理工大学经济管理学院,山西 太原 030024)
煤矿区应急救援站的选址问题是关乎煤矿生产安全的重要一环,决策者需要考虑时间、成本和资源等多个影响决策的因素,尤其是需要优先考虑应急救援的时效问题。首先利用p-center选址模型,基于时间目标选择出应急救援站候选地址;然后通过多目标决策模型,综合考虑时间、成本和资源三个目标进行决策,并利用线性加权法求解模型,最终从应急救援站侯选地址中选择出最合理的煤矿区应急救援站的地址;最后引用实例详细说明了煤矿区应急救援站选址决策的实现过程,指导和帮助煤矿区决策者对矿区应急救援站选址问题做出科学决策。
煤矿区;应急救援站;p-center选址模型;多目标决策
煤炭工业是我国工业生产中伤亡事故最严重的行业之一,煤矿事故一旦发生,就会造成极大的人员伤亡及财产损失[1]。随着我国对于煤矿安全的重视程度不断提高,对于煤矿安全研究的投入也大幅增加,煤矿应急救援工作也越来越受到重视。在无法避免由于人为、技术、自然等因素导致的灾害事故时,通过提高煤矿应急救援能力,增加煤矿人员、资源和环境的突发事故抵抗力,已经逐渐成为煤矿安全工作的关键[2]。
对于煤矿区来说,矿区应急救援站是应对煤矿突发事故很重要的一环,矿区应急救援站的建设已经成为煤矿区安全工作的重要组成部分。煤矿区通常分布有若干个煤矿,矿区应急救援站要求能够对煤矿区内所有煤矿的应急救援工作提供防灾减灾服务和支持。在煤矿突发事故发生后,对于应急救援时效的要求极为严苛,甚至可以说是分秒必争,而且煤矿事故往往是多地点多事故并发,事故地点通常没有规律性。考虑到这些因素,要保证煤矿区应急救援站的服务范围能够涵盖矿区内所有煤矿,则矿区应急救援站的选址就显得至关重要。目前设施选址决策问题的研究,常用的方法有p-中值模型(p-center模型)、集合覆盖模型、最大覆盖模型等。胡德慧等[3]采用p-中值模型来解决物流系统回收中心(非紧急设施)的选址决策问题;江元等[4]利用集合覆盖模型寻求电费缴纳点选址成本最小化;李竞等[5]利用广义最大覆盖模型寻求公路养护应急中心服务范围的最大覆盖化。尽管对选址决策模型的研究已经日趋成熟,但大多数选址研究都只考虑单个决策目标,而煤矿区应急救援站的选址问题需要考虑多个目标的影响。因此,本文采用p-center和多目标决策相结合的模型,综合考虑多方面的影响因素之后决策出煤矿区应急救援站的最佳地址。这种选址决策方法更能适应煤矿区应急救援时效要求高、成本与资源目标兼顾的要求,可以更好地指导煤矿区应急救援站的选址决策工作。
1 基本原理
在社会经济系统的研究中往往面临的是多目标的决策问题,这些目标之间既相互联系又相互制约,使决策过程复杂化,让决策者难以轻易做出决策,只有对多种因素目标进行综合考虑,才能做出合理的决策[6]。煤矿区应急救援站的选址决策问题就是一个多目标决策问题。
由于煤矿突发事故往往无法事先预测,且破坏力大、伤害性强,因此在煤矿突发事故发生后,应急救援具有如下特点:应急救援的效果会随着救援时间的延长而逐渐下降,所以矿区应急救援站与事故煤矿的距离应尽可能地小[7];矿区应急救援站的设立需要投入大量资金和资源,因此要科学合理地考虑应急救援站的建设及使用成本,以免造成资源浪费;一旦有多个煤矿发生突发事故,在短时间内就需要大量应急资源,这时仅凭应急救援站的资源很难满足事故煤矿的应急需求,因此还需要从应急救援站地址附近补充应急资源。本文综合考虑了煤矿应急救援的这些特点,将煤矿区应急救援站的选址决策目标归纳如下:
(1) 时间目标:考虑应急救援问题时间上的紧迫性,要求从应急救援站出发到达事故点的时间要尽可能短,时间目标是煤矿区应急救援站的选址决策问题的首要优化目标[8]。
(2) 成本目标:考虑经济性和预算约束,在满足应急救援需求的情况下,要求应急救援站的数目尽可能少,同时还需要考虑救援站地点的土地成本以及救援站到事故点的单位运输成本[9]。
(3) 资源目标:考虑事故点对资源的需求,对于矿区内的某一煤矿事故点,从理论上最好的措施是从最近的应急救援站进行救援,而且这个救援站的资源能够满足该事故点的资源需求。如果该应急救援站的资源无法满足事故点的需求,那就需要从剩下的应急救援站中找出最近的应急救援站对该事故点进行救援,或者从应急救援站的附近补充新的资源以支援应急救援工作。
本文首先基于时间目标确定煤矿区应急救援站候选地址,建立了p-center选址模型。煤矿区突发事故往往影响的是矿区内多个煤矿的安全生产,因此必须考虑应急救援站对矿区内所有煤矿的“易接近性”。如果应急救援站距离煤矿太远,需要救援的煤矿就要等待过长的时间,影响应急救援的效果。可见,衡量应急救援站位置有效性的重要指标就是所有煤矿到达应急救援站所在位置的平均距离[10]。确定应急救援站候选地址也就是确定p个矿区应急救援站,使p个矿区应急救援站到达各个煤矿的时间符合煤矿安全救援的时间要求。在确定煤矿区应急救援站候选地址之后,再通过多目标模型进行决策,利用线性加权法求解模型,基于时间目标、成本目标和资源目标,综合考虑救援时间、救援成本和救援效果,从应急救援站候选地址中选择出最合理的矿区应急救援站的地址,指导和帮助煤矿区决策者在矿区应急救援站选址问题上做出科学决策。
2 模型构建
2.1p-center选址模型
p-center选址模型定义如下:G为平面内的网络,G=(U,E),其中U=(X,V)为G网络内的点集[X为G内的顶点集,X={x1,x2,…,xp|xi∈G,i=1,2,…,p};V为弧上的非顶点集,称为内点],E为G内任意两个顶点间弧线的集合,弧长为eij;H={hi}为点ui的权重,W={wi}为弧长eij的权重[11]。对于G内的任意两点a、b来说,t(a,b)表示从a点到b点的最短路径所花费的时间,d(a,b)表示从a点到b点的最短路径。由于时间目标无法科学量化,在不考虑运输速率差别的前提下,本文将时间目标转换为距离目标来进行实际计算。
相对而言,如果网络G中某一顶点与其相隔最远的顶点的距离在所有顶点中最近,则称其为G的顶点中心;如果网络G中某一顶点与其相隔最远的点的距离在所有顶点中最近,则称其为G的一般中心;相对应的,如果网络G中某一点与其相隔最远的顶点的距离在所有点中最近,则称其为G的绝对中心;如果网络G中某一点与其相隔最远的点的距离在所有点中最近,则称其为G的一般绝对中心[12]。
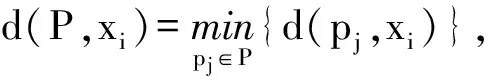
min{max(hi,d(P,xi))}
s.t.|P|=p
当P⊂X时,则模型为顶点p-center选址模型;当时P⊂U时,则模型为绝对p-center选址模型。从理论上来讲,绝对p-center选址模型更为科学,但是基于煤矿区的具体情况,应急救援站设置在煤矿附近可以借用煤矿的一些基础设施,而且很多非顶点的地方其地形地貌并不适合设立应急救援站。所以本文主要研究的是顶点p-center选址模型,根据最长路径O(n)算法,局部中心距离必然为最长路径距离的一半,即给定任意的顶点xi,找出距离xi最远的顶点xj,再找出距离xj最远的顶点xt,xi到xt的路径就是所寻的最长路径。
模型算法如下:
(1) 设距离目标为s。
(2) 若有n个顶点,则根据图中各顶点的最短距离构建n阶最短距离矩阵F和最短路径矩阵L。
(3) 令k=1,k=1,2,…,n。

(6) 令k=k+1,若k (7) 列出局部中心距离d*(xk)统计表,比较d*(xk)与距离目标s,从中找出满足d*(xk)≤s的d*(xk);从小到大排列d*(xk),取最小的p个d*(xk)相对应的顶点。 (8) 若满足条件的d*(xk)的个数小于p,则将符合条件的局部中心距离d*(xk)分别沿相邻顶点方向移动s-d*(xk)距离作为新的顶点,然后从中选出p个顶点。 上述顶点集合即为所求应急救援站候选点集p。 2.2 多目标决策模型 对于p-center选址模型所得出的p个应急救援站候选地点,利用多目标决策模型可以进一步筛选出煤矿区应急救援站的选址地点。 多目标决策问题的一般模型为 minz(x)=[z1(x),z2(x),…,zm(x)] s.t.x∈X (1) 式中:X为决策空间可行域;x为决策问题的m个决策变量,当x∈X时,x也可视为可行解;z1(x),z2(x),…,zm(x)为决策问题的m个目标函数。 由于m个目标之间往往不具备共同度量性,甚至互相矛盾,所以通常无法找到一个能使所有目标同时达到最优的解。因此,本文研究多目标决策问题的目的是寻求一个可行解,利用线性加权法求解模型[13]。 本文构建的煤矿区应急救援站多目标决策模型如下: 设矿区有煤矿集合I,需要从p个候选地点选择应急救援站集合J。 对于时间目标问题,该问题的特点是同时考虑应急救援的公平性和效率性。公平性要求矿区应急救援站能服务所有煤矿的应急需求;效率性要求矿区应急救援站到所有煤矿的平均加权距离最小[14],即 (2) 对于成本目标问题,该问题的特点是在保证应急救援的前提下,尽可能地实现成本最小化。即 (3)式中:Cj表示成本目标;Qj表示应急救援站j处的建设成本(土地、建设及运行等成本);dijcij表示应急救援站j至煤矿i的运输成本,其中cij表示应急救援站j至煤矿i的单位运输成本(同路面条件、交通负荷等有关),dij表示应急救援站j至煤矿i的距离。 对于资源目标问题,该问题的特点是选取离事故煤矿最近的救援站参与应急救援,如果该救援站的全部救援资源无法满足事故煤矿的需求量,则再选取第二近的救援站参与应急救援,如此等等,直到满足应急物资的需求。即 Rj=rj s.t.i∈I,j∈P (4) 式中:Rj表示资源目标;rj表示应急救援站j所在地的资源储备量。 设多目标决策的决策目标为Z,p个候选地点的决策目标分别为z1,z2,…,zp。采用线性加权法求解多目标决策模型,主要是将多目标决策问题转化为单目标决策问题来求解,这样可以基于决策者对各目标的决策偏好确定权重,通过对不同目标赋予不同的权重值来反映不同目标对于综合决策的影响程度[15]。对于本文的成本目标、时间目标和资源目标根据影响度分别赋予权重y1,y2,y3,考虑到成本目标、时间目标对综合决策目标的影响是负相关影响,而资源目标对综合决策目标的影响是正相关影响,则多目标决策函数可表示为 (5) 将z1,z2,…,zp从小到大排列,选择最小的|J|个点作为应急救援站的地址。 本文以某煤矿区应急救援站的选址为例,通过构建煤矿区应急救援站多目标决策模型进行实例分析。该矿区有8个煤矿,矿区分布如图1所示。每一个顶点对应一个煤矿,X1代表1号煤矿,X2代表2号煤矿,以此类推,X8代表8号煤矿。 根据煤矿突发事件的未知性,定义每个煤矿发生事故的概率是相等的,边长代表顶点之间的距离,考虑到煤矿区应急救援的特点,要求最近的应急救援站到煤矿的救援时间在5 h以内,在满足时间目标的前提下,在矿区内选取3个应急救援候选地址,最终确定一个最优的应急救援站地址。 根据各项数据建立p-center选址模型。由于各个煤矿发生突发事故的概率是一样的,所以各顶点的权重相同。为方便模型计算,取各顶点的权重hi=1(i=1,2,…,|I|);由时间目标计算得到距离目标s=8。根据各点之间的边长可以构造出最短距离矩阵F和最短路径矩阵L如下: 根据顶点p-center选址模型的算法,可以计算出各顶点局部中心距离d*(xk),其计算结果见表1。由于算法计算过程繁琐,在此不再赘述。 根据距离目标s=8,符合d*(xk)≤s条件的有X3、X4、X5、X6、X7、X86个顶点,因此选取X6、X7、X83个煤矿作为应急救援站的候选地址,并由多目标决策模型来确定最终的应急救援站地址。 对于时间目标,基于公平性原则所有煤矿在应急救援中应该一视同仁,为方便计算设ai=1,X6、X7、X8这3个候选地址到所有煤矿的加权平均距离见表2。由公式(2)计算得到时间目标结果如下:T6=13.25,T7=12.75,T8=12.625。 表2 3个候选地点到所有煤矿的加权平均距离 对于成本目标,3个候选地址到达不同煤矿的单位运输成本见表3。根据各应急救援站候选地址的相应建设成本(土地、建设及运行等成本),Qj取值如下(单位:万元):Q6=100,Q7=105,Q8=110。由公式(3)计算得到成本目标结果如下:C6=200.8,C7=207.4,C8=205。 表3 3个候选地址到达不同煤矿的单位运输成本 对于资源目标,由各应急救援站候选地址的物资储备量,可计算得各应急救援站候选地址的资源目标结果如下:R6=133,R7=125,R8=129。 对于时间、成本和资源各目标权重的选择,本文根据煤矿应急救援站选址的特点,遵循先考虑时间目标,故各指标权重确定为:y1=0.5,y2=0.3,y3=0.2。 由公式(5)将多目标问题转化为单目标问题,得 由计算结果可知,利用多目标决策模型可以确定煤矿X6为该煤矿区应急救援站建设地址。由于各个候选地址位置相距不远,加之地理地形条件差别不大,因此很多影响最终决策目标的因素之间数据没有太大的差异,这也导致最终各个候选地址的决策目标z值差异不大[16],但这并不影响多目标决策模型在煤矿区应急救援站选址问题上的应用。 煤矿区应急救援站的选址决策问题是一个多目标的决策问题,需要综合考虑时间、成本和资源三个目标[17],但由于应急救援对于时效的严苛要求,因此时间目标需要优先考虑。通过顶点p-center选址模型的应用过程可以看出,顶点p-center选址模型在针对时间目标的选址问题上具有较强的应用性,而运用线性加权法求解多目标选址决策模型更合理,有助于理清各决策目标之间的复杂关系,且计算过程简单明了,计算结果科学明确。通过对具体实例的算例分析表明,基于p-center的多目标选址模型对于煤矿区应急救援站的选址决策具有较强的实用价值。 [1] 张贤凯,周劲松,陈春歌,等.我国煤矿安全生产领域构建保险体系的探讨[J].安全与环境工程,2010,17(6):83-87. [2] 方磊,何建敏.城市应急系统优化选址决策模型和算法[J].管理科学学报,2005,8(1):12-16. [3] 胡德慧,钱瑛,熊琦,等.回收物流系统中回收中心选址模型优化[J].物流科技,2013,36(5):89-91. [4] 江元,王冰,张婷,等.基于集合覆盖模型的电费缴纳点选址研究[J].中国电力,2013,46(2):60-64,71. [5] 李竞,王超.应用广义最大覆盖模型进行公路养护应急中心布局选址研究[J].交通标准化,2013(1):20-23. [6] 陈志宗,尤建新.重大突发事件应急救援设施选址的多目标决策模型[J].管理科学,2006,19(4):10-14. [7] 李创起,景国勋,张永强,等.模糊评价方法在煤矿安全管理中的应用[J].安全与环境工程,2012,19(1):87-89,94. [8] 廖炳英,毕凌岚.应急避难场地“就近布置”规划原则探讨[J].安全与环境工程,2010,17(2):18-21. [9] 方磊,何建敏.应急系统优化选址的模型及其算法[J].系统工程学报,2003,18(1):49-54. [10]蒋慧.应急物流配送中心选址研究[D].成都:西华大学,2010. [11]曹宇峰.不确定环境下应急物流设施选址与运输优化[D].郑州:河南科技大学,2009. [12]赵小明,王利.基于P-中心法的农资配送中心选址研究——以辽宁省昌图县为例[J].安徽农业科学,2012,40(25):12691-12693. [13]安伟刚.多目标优化方法研究及其工程应用[D].西安:西北工业大学,2005. [14]王占武,唐凯,严良,等.基于熵权TOPSIS法的火电厂选址综合决策[J].安全与环境工程,2011,18(5):103-106. [15]张兰,邱贤德,李林,等.浅析安全系统与安全管理系统[J].矿业安全与环保,2004,31(3):21-23. [16]陈志宗.城市防灾减灾设施选址模型与战略决策方法研究[D].上海:同济大学,2006. [17]魏汝营,陈建宏,杨立兵,等.突发事件应急救援设施选址决策模型[J].工业安全与环保,2009,35(11):50-52. Location Selection for Emergency Rescue Station of Coal Mining Area Based on Multi-objective Decision WANG Yayang,WANG Hanbin (SchoolofEconomicsandManagement,TaiyuanUniversityofTechnology,Taiyuan030024,China) The location problem of emergency rescue station is an important part of safety production in coal mine.The decision-makers need to consider the factors,time,cost and resources,especially the efficiency of emergency rescue.In view of the character,this paper firstly selects out the candidate locations of emergency rescue station by p-center model based on the time target;then the paper uses the multi-objective decision model to make a decision with considering three targets including time,cost and resources.Finally the paper applies the linear weighted summation model to determine the address of the emergency rescue station of coal mining area.The paper references instances to detail the implementation processes of the location decision. What’s more,the paper helps decision-makers from coal mining area to choose the right location of emergency rescue station with some instances of the implementation processes of selecting the emergency rescue station in detail. coal mining area;emergency rescue station;thep-center location selection model;multi-objective decision 胡丽琴(1981—),女,博士,副教授,主要从事可靠性与概率安全分析方法等方面的研究。E-mail:liqin.hu@fds.org.cn 1671-1556(2015)01-0121-05 2014-03-15 2014-11-27 王亚阳(1990—),男,硕士研究生,主要研究方向为矿业管理及安全系统工程。E-mail:wy30240@163.com X913.4;X A 10.13578/j.cnki.issn.1671-1556.2015.01.022
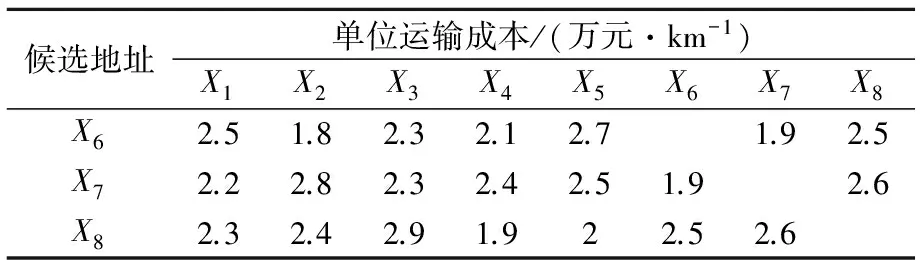
3 算例分析

4 结 论
