Ship hull optimization based on wave resistance using wavelet method*
2015-04-20ZHAOYong赵勇ZONGZhi宗智ZOULi邹丽
ZHAO Yong (赵勇), ZONG Zhi (宗智), ZOU Li (邹丽)
1. Transportation Equipment and Ocean Engineering College, Dalian Maritime University, Dalian 116026, China 2. State Key Laboratory of Ocean Engineering, Shanghai Jiao Tong University, Shanghai 200240, China,E-mail: fluid@126.com 3. State Key Laboratory of Structural Analysis for Industrial Equipment; School of Naval Architecture, Dalian University of Technology, Dalian 116024, China
Introduction
The wave resistance is very sensitive to the ship hull surface, which might be reduced by a large proportion through the hull optimization in a high-speed situation[1-3]. Therefore, the ship hull optimization is of a very important engineering significance. The ship hull surface must be expressed in a form, which is a prerequisite in the optimization. Normally, the hull surface or its derivative function is expressed by the non-uniform rational B-spline (NURBS) in many blocks due to complexity of the hull surface as in Refs.[4-6]. In this paper, we express the whole hull surface by a wavelet expression and then derive a wave resistance formula in the wavelet space and optimize the hull surface aiming to reduce the wave resistance, as a new approach for the hull optimization.
Since the 1980s, the study of the wavelet has made a great progress, especially by the work of Grossmann and Morlet, Dauberchies[7]and Taswell[8].Since then, the wavelet method has found many applications in the field of signal and image processing.Due to wavelet bases’ unique properties, such as the compact support, the multi-scale resolution and the fast decomposition algorithm, the wavelet analysis enjoys great potential advantages in the numerical calculations as compared to the Fourier analysis. By expressing functions into the wavelet series, the information of the multi-resolution and the localization of the function can be easily identified, thus the wavelet can serve as a mathematical microscope. By setting a threshold for the wavelet coefficients, the local structure can be captured, while the global error is controlled by this threshold. The wavelet method is well suitable in solving those problems with its multi-scale propertyand local structure[9-11]. As a preliminary study, we firstly utilize the wavelet method to solve the wave resistance problem based on the Michel theory for a Wigley model and then to optimize the hull in this paper.
1. An outline of wavelet
The wavelet method enjoys such properties as the compact support, the symmetry, the orthogonality, and the bi-orthogonality. Compared to the Fourier transform, the compact supported bases in the wavelet is a significant improvement. The wavelet transformation of a function converts the function into a series of small wave-like bases, allowing the function to be stored in an efficient way. The wavelet method has great advantages in solving the problems characterized by multi-scale and local structures, such as the turbulence and wave resistance problems. Here we will discuss some basic properties of the wavelet bases.
For a given functionf(x), we can measure the component with a scaleaaround the positionbby the following process

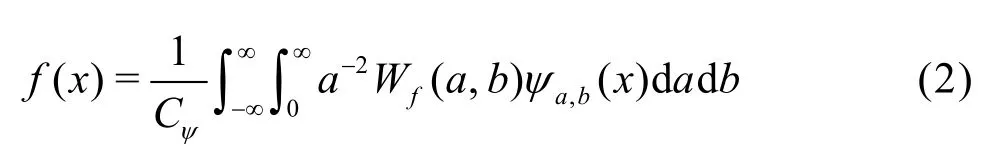
where

Cψ<∞ is called the admissibility condition. The vanishing moment is an important index. The wavelet has anNorder vanishing moment under the condition that

For example, if a polynomial is less thanNorder, its wavelet coefficients are zero if we choose a particular wavelet with anNorder vanishing moment. This property leads to an effective compression in the wavelet method.
In the practical numerical method, we often use discrete wavelet transformations. The bases of the wavelet are formed by dilation and translation of a mother wavelet functionψ(x) as

wherej,k∈Z,jis the scale index,kis the location index. The functionψ(x) has a companion, the scaling functionφ(x), and these functions satisfy the following relations:
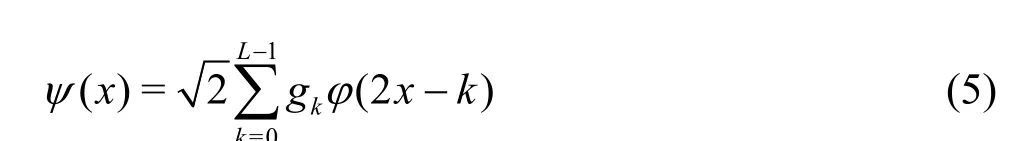
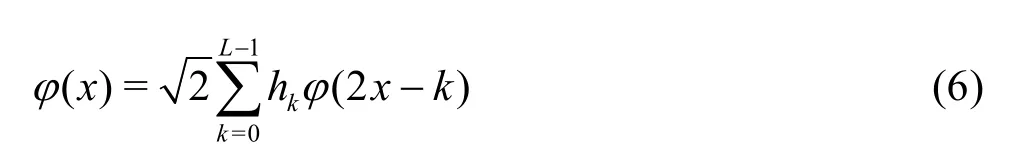

Similarly, the bases of the scale function are formed by dilation and translation of a mother scale functionφ(x)
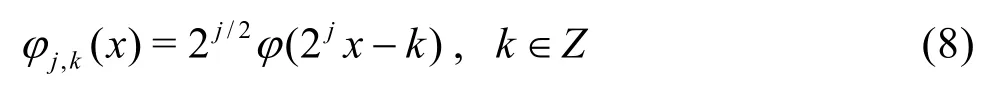
Two-dimensional bases can be formed by the tensor product of one dimensional bases in the following way,


The Dauberchies wavelet does not have an explicit expression, but can be generated at any scale using the scale formula in an iterative manner.
The wavelet bases provide us a multi-scale resolution to express a function. It is assumed that the functionf(x) can be well approached on the finest scaling indexJ, i.e.,, and then it can be decomposed in terms of the sum of a series of wavelet base functions

The coefficients are obtained by the wavelet decomposition formula:

For functions that contain isolated small scales on a large scale background, most wavelet coefficients are small, thus we can retain a good approximation even after discarding a large number of wavelets with small coefficients. This situation can be explained by the wavelet’s vanishing moment. More precisely, if we rewrite the approximation as a sum of two terms composed, respectively, of wavelets with absolutely value beyond and below a prescribed particular thresholdε,
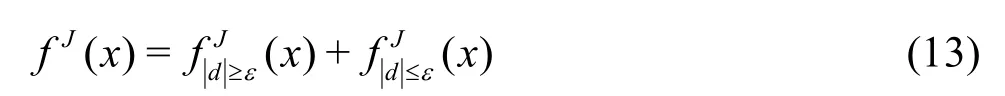
where
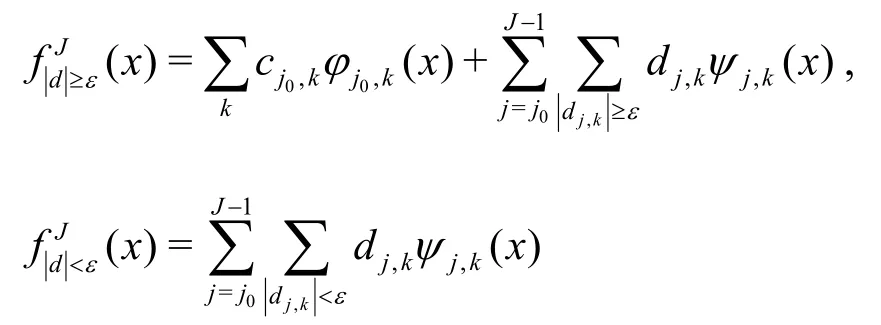
According to Vasilyev and Kevlahan[12], the approximation error by the significant wavelets whose coefficient amplitude is above the thresholdεis bounded by the following restriction:

And the number of the significant wavelet coefficientsKis bound byεand the wavelet’s vanishing momentNas

The coefficients in Eqs.(14) and (15) depend on the wavelet vanishing moment and the functionf(x).The threshold plays two roles: making the approximation adaptive, and controlling the approximation error globally. The similar situation can be simply extended to the multi-dimensional space by the tensor product.In the next section, we will have the ship hull surface’s wavelet expression and verify the accuracy by the Wigley model.
2. Hull surface’s wavelet expression
Assume that the smallest scale information of the hull surface can be identified on scaleJ, denoted byfJ(x,y), with the initial scale coefficients=, we might do the decomposition until the largest scale is reached, which can be expressed by the following multi-scale wavelet expression

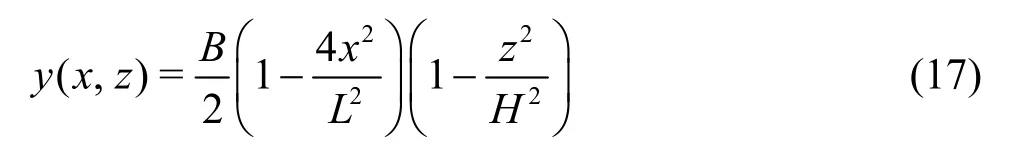
Here we chooseB=0.2m,L=2m,H=0.125 m. We approximate it in the finest scaleJ=6,repeating the decomposition at the coarsest scaleJ0=2 with the Db2 wavelet. We choose the thresholdε=1.0 × 10-3, the resulting 436 wavelet coefficients are kept instead of 4 096, which means that with less then 10% of the coefficients, the complete information can be captured in the finest scaleJ=6 at an accuracy loss in the order ofε=1.0× 10-3, which can be verified by the error distribution as shown in Fig.1.

Fig.1 Error distribution of reconstructed Wigley model
3. Hull optimization based on Michel theory in wavelet expression
Based on the linear theory, the wave resistance can be calculated by the Michel formula in Gotman[13]


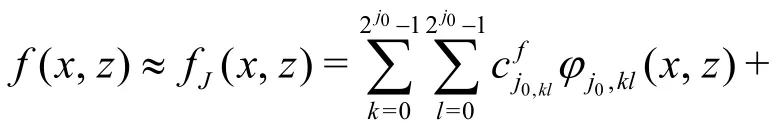

Using the orthogonal property of the wavelet bases of the same scale, we have

And the wavelet space orthogonal property says

The integral calculation can be simplified as the product of the corresponding wavelet coefficients,

The ship hull surface’s wavelet coefficients are used as the optimization variables, according to the property that the wavelet function’s integral is equal to zero

It is concluded that the volume does not change with the optimization variables. Denoting the change of the ship hull surface’s wavelet coefficients as, we obtain the target function

where

In summary, we need to find the optimal solutionto make the following expression minimum if.
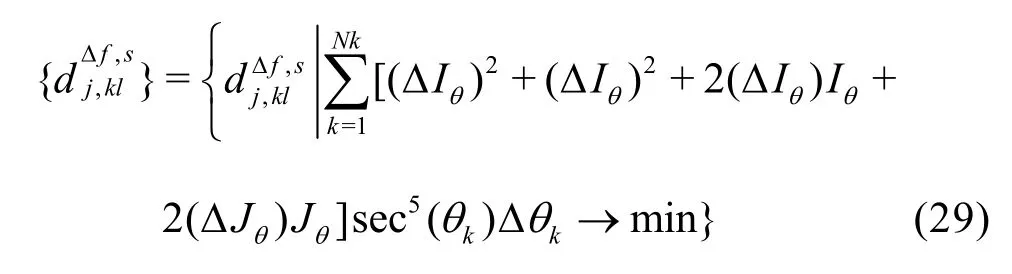
Furthermore, we use the wavelet method’s features of the multi-scale resolution and the spatial localization to analyze each optimization variable’s contribution in the resistance, and then choose those with a significant contribution, thus reducing a large number of optimization variables.

Fig.2 Wave resistance coefficient for Wigley reconstruction at several scales

Fig.3 Wave resistance coefficient by wavelet coefficients on separated scales

Fig.4 The distributions of the quadratic sums of Wigley ship’s wavelet coefficients at j=5,4,3,2
In what follows, we analyze the wave resistance distribution on scales and locations. For the scale indexj, we reconstruct the ship surface on various scales, from the coarsest to the scalej,Substituting it into the wave resistance formula (21),we obtain the relation of the resistance coefficient versus the Froude number, as shown in Fig.2.
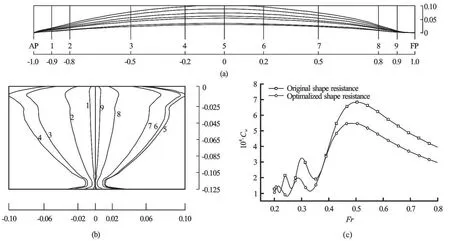
Fig.5 Molded lines of Wigley ship after optimization
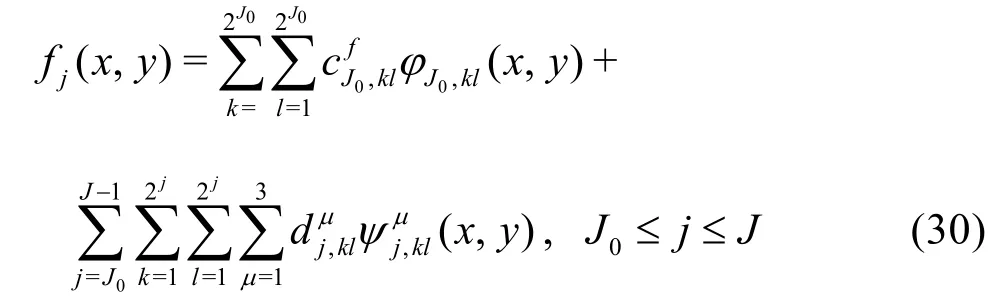
To observe the resistance on a separated scale,we can consider the difference between the resistances of adjacent scales, for example, if we want to see the resistance due to the wavelet coefficients on the scalej=2, we might consider the difference between the resistances on the scalesj=3 andj=2. Figure 3 shows the wave resistance on each scale. It is shown that the wavelet coefficients on the scalej=2 play an important role, thus we choose them as the optimization variables.
Next we analyze the wave resistance’s spatial distribution by the wavelet coefficients’ spatial distribution. Figure 4 shows the sum of the squares of the wavelet coefficients in three directions, i.e., the horizontal, the vertical, and the diagonal directions, and it is found that the large values are localized near the ship head and the waterline, as is consistent with the real situation. Moreover, at the scalej=2, the amplitude is much larger than at other scales, and they are uniformly distributed. Based on the above observation,we select the wavelet coefficients on the scalej=2,totally 48 variables, to be the final optimization variables.
We use the genetic algorithm to optimize these 48 variables on the designedFr=0.3, and the results are shown in Fig.5. The wave resistance is reduced by 49.6%. The resulting hull is flatter near the hull’s bow and stern, convex under the waterline, and then contracted sharply near the the waterline. The bottom is a clear plate and then a sharply inward contraction. The optimized hull transfers a partial volume from the water surface nearby to a certain distance below the waterline. However, this hull does not meet the smoothness requirement in real engineering sense. Also, the frictional resistance should be increased for this kind hull. It should be noticed that we obtain this optimal hull mainly based on the mathematical consideration by the wavelet method.
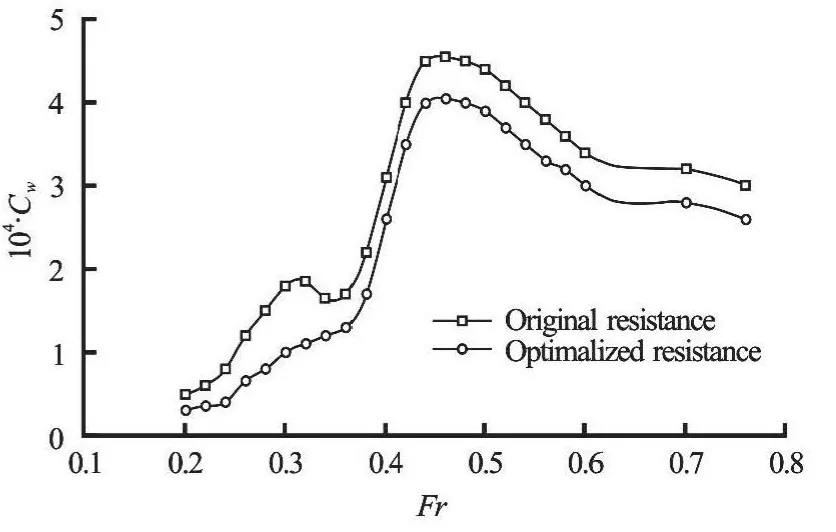
Fig.6 Comparison of wave resistance coefficients of Wigley hull and its optimal hull using wavelet approach by Michel theory calculating by Noblesse theory
In order to check the drag’s reduction, the wave resistance after optimization using the wavelet approach by the Michell theory is calculated by the Noblessewave resistance theory for a slender ship[14], as shown in Fig.6.
In the Noblesse theory, the original hull’s wave resistance coefficient is 1.8×10-4, while the optimized hull’s coefficient is reduced to 1.2×10-4, one third wave drag reduction at the designedFr=0.3. The drag reduction proportion is less than the previous calculation. This result is reasonable due to the different features of the Michel and Noblesse theories. From these consistent results, we may see that the proposed model is rational and the calculation is accurate.
4. Conclusions
Utilizing the excellent mathematical properties of the wavelet, such as the compact bases, the orthogonal subspace partition and the fast algorithm for decomposition and reconstruction[15,16], we find its application in the ship hull surface optimization by reducing the wave resistance in this paper. Firstly, the hull surface is expressed by the wavelets with a fine enough scale,secondly, the expression is approximated by introducing a threshold for the wavelet coefficients, thus a very concise approximate expression is obtained with an error of the order of the threshold, thirdly, the wave resistance formula is derived in the wavelet form, and fourthly, the wavelet coefficients of the hull surface are chosen as the optimization variables, while the hull volume keeps constant. A good understanding of the wave resistance’s distribution is obtained in terms of scales and locations in the wavelet language. The wavelet method provides a new approach for the hull optimization.
As a preliminary study, we adopt the linear wave resistance theory and a simple hull model. The smoothness constraint is not included in the optimization process, so the optimal hull may not meet the actual requirements in ship engineering. We are considering a further research in terms of the non-linear wave resistance theory as in Refs.[17,18], and the practical hull surface and smoothness requirements.
Acknowledgement
This work was supported by the Open Research Fund of State Key Laboratory of Ocean Engineering,Shanghai Jiao Tong University (Grant No. 1402).
[1] ZHANG Bao-ji, MA Kun and JI Zuo-shang. The Optimization of the hull form with the minimum wave making resistance based on Rankine source method[J].Journal of Hydrodynamics, 2009, 21(2): 277-284.
[2] WANG Yan-ying. Fine optimization of ship hull lines in resistance performance by using CFD approach[J].Journal of Dalian University of Technology, 2002,42(2): 127-133(in Chinese).
[3] WANG Zheng, LU Xiao-ping. Research on high speed surface warship with bulbous bow[J]. Journal of Hydrodynamics, Ser. A, 2006, 21(6): 789-795(in Chinese).
[4] KOELMAN H. J., BASTIAAN N. A technical note on the geometric representation of a ship hull form[J].Computer-Aided Design, 2013, 45(11): 1378-1381.
[5] SHAMSUDDIN S. M., AHMED M. A. and SMIAN Y.NURBS skinning surface for ship hull design based on new parameterization method[J]. International Journal of Advanced Manufacturing Technology, 2006,28(9): 936-941.
[6] SHI G., LIU S. and CHEN P. A fast NURBS interpolation method for 3D ship hull surface[J]. Journal of Applied Sciences, 2013, 13(12): 2139-2145.
[7] DAUBECHIES I. Orthonormal bases of compactly supported wavelets[J]. Communications on Pure and Appllied Mathmatics, 1988, 41(7): 909-996.
[8] TASWELL C. The what, how, and why of wavelet shrinkage denoising[J]. IEEE Computational Science and Engineering, 2003, 3(2): 12-19.
[9] HUANG M. C. Wave parameters and functions in wavelet analysis[J]. Coastal Engineering, 2004, 31(1):111-125.
[10] SCHNEIDER K., VASILYEV O. V. Wavelet methods in computational fluid dynamics[J]. Annual Review of Fluid Mechanics, 2009, 42: 473-503.
[11] CAI Jun-meng, YI Wei-ming and HE Fang et al. Research on crude oil thixotropy based on discrete stationary wavelet transform[J]. Journal of Hydrodynamics, Ser.A, 2005, 20(6): 683-688(in Chinese).
[12] VASILYEV O. V., KEVLAHAN N. K. R. An adaptive multilevel wavelet collocation method for elliptic problems[J]. Journal of Computational Physics, 2005,206(2): 412-431.
[13] GOTMAN A. S. Study of Michell’s Integral and Influence of viscosity and ship hull form on wave resistance[J]. Oceanic Engineering International, 2002,6(2): 74-115.
[14] NOBLESSE F. A slender-ship theory of wave resistance[J]. Journal of Ship Research, 1983, 271(1): 19-33.
[15] ZHAO Yong, ZONG Zhi and ZOU Wen-nan. Numerical simulation of vortex evolution based on adaptive wavelet method[J]. Applied Mathematics and Mechanics (English Edition), 2011, 32(1): 33-44.
[16] ZONG Zhi, ZHAO Yong and ZOU Wen-nan. Numerical solution for differential evolutional equation usingadaptive interpolation wavelet method[J]. Journal of Computational Mechanics, 2010, 27(1): 65-69(in Chinese).
[17] YANG C., HUANG Fuxin. and NOBLESSE Francis.Practical evaluation of the drag of a ship for design and optimization[J]. Journal of Hydrodynamics, 2013,25(5): 645-654.
[18] HUANG F., YANG C. and NOBLESSE F. Numerical implementation and validation of the Neumann-Michell theory of ship waves[J]. European Journal of Mechanics-B/Fluids, 2013, 42(1): 47-68.
猜你喜欢
杂志排行
水动力学研究与进展 B辑的其它文章
- A general framework for verification and validation of large eddy simulations*
- Direct calculation method of roll damping based on three-dimensional CFD approach*
- Visualization study on fluid distribution and end effects in core flow experiments with low-field mri method*
- Large-eddy simulation of the flow past both finite and infinite circular cylinders at Re =3900*
- Safe operation of inverted siphon during ice period*
- Flow field simulation of supercritical carbon dioxide jet: Comparison and sensitivity analysis*
