窄波束引信飞行试验启动参数计算精度分析

裴 喆， 杨志群

（92941部队，辽宁 葫芦岛125000）

0 引言

舰空导弹经常采用窄波束定角侧向探测的无线电或激光引信，这类引信在抗干扰和探测导弹类目标方面具有一定优势。由于波束窄，引信在大目标上的探测和启动区域很小。这类引信飞行试验时，计算的主要启动参数是启动部位和启动距离。启动参数是靶场飞行试验结果分析的重要部分，其计算精度直接影响引战配合效果、导弹杀伤概率的分析。启动参数是在实弹飞行条件下，验证引信启动特性的重要依据。关于利用飞行试验数据计算引信启动参数的方法，未见文献进行专题研究。本文研究窄波束引信启动参数计算方法，并仿真分析相关误差因素影响下的计算精度。

1 引信启动参数计算方法

1.1 窄波束引信启动参数计算原理

地面坐标系oxyz中的遭遇段弹目交会姿态及窄波束侧视引信探测模型如图1所示。图中F表示引信，Ω 表示波束主瓣倾角，R 表示启动距离，目标上的Tj点表示引信启动部位。引信波束绕弹轴360°形成一个空心圆锥。oMxMyMzM为弹体坐标系，导弹尾部发动机喷口火焰为光测点，将其设为弹体坐标系的原点。

图1 窄波束侧视引信探测模型

引信启动参数计算步骤：首先利用弹目几何参数、拟合处理后的试验光测外弹道数据，计算引信和目标的运动轨迹；然后根据引信倾角固定、波束窄、探测区域小的特性，并利用遥测记录的引信启动时间，计算引信启动部位和启动距离。

当引信探测到目标，但未构成启动条件时，可根据遥测记录的引信回波信号，计算出引信探测部位和距离，用于分析引信探测灵敏度或靶标散射特性。

1.2 同侧双站光学外弹道测量模型

舰空导弹海上飞行试验时，要利用经纬仪进行光学外弹道测量。经纬仪通常沿海岸同侧布站。测量弹目遭遇段数据时，常采用双站同帧画幅法，该方法可有效减小测量误差［1，2］。在地面坐标系oxyz 中建立同侧双站光学外测模型［2］，如图2所示。图中，O1和O2表示双站经纬仪，坐标分别为（xO1，yO1，zO1）和（xO2，yO2，zO2）；M和T表示导弹和目标，光测点坐标分别为（xM，yM，zM和（xT，yT，zT）。

图2 同侧双站光学外测模型

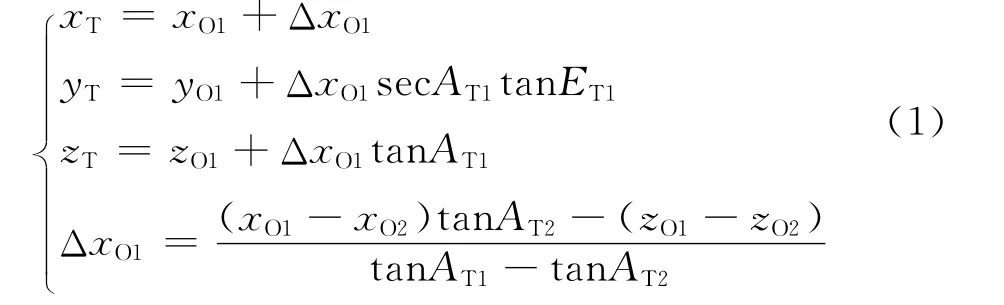
经纬仪测量误差包括系统误差和随机误差。系统误差包括时间误差、跟踪部位误差、大气折射误差等，这些误差一般可以进行修正［3-4］。本文不讨论系统误差的修正，只讨论随机误差对计算精度的影响。随机误差主要包括测角误差和事后画幅光点判读误差。测角误差无法修正，通常服从均值为零的正态分布［3-4］。当跟踪目标成像较好时，事后判读结果平稳且精度较高；目标成像不好时，判读结果摆动且精度较低。多次判读得到的测量值是以算术平均值为中心集中分布的［5］，可以认为判读误差也服从均值为零的正态分布［6］。

由于弹目遭遇时间很短，可认为弹目均作匀速直线运动。因此，可利用最小二乘直线拟合的方法对弹目三维方向光测数据分别消除误差，拟合得到的弹目光测点运动轨迹分别为［xMn（t），yMn（t），zMn（t）］和［xTM（t），yTM（t），zTM（t）］。下标“n”表示拟合。

1.3 飞行试验引信启动参数计算方法

（1）计算引信运动轨迹

首先，将引信F 处的弹体坐标（xMF，yMF，zMF）转换为地面坐标（xF，yF，zF），表达式为［7］

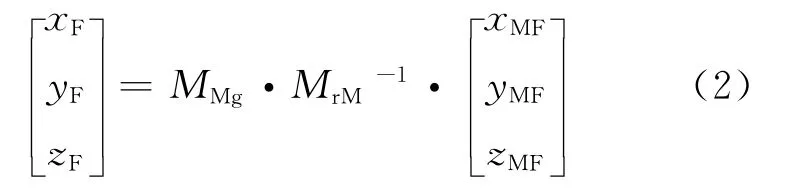
其中：

式中：MMg为导弹速度坐标系与地面坐标系的转换矩阵；φM和θM分别为速度偏角和弹道倾角，可在弹体坐标系计算得到［7］；MrM为导弹速度坐标系与弹体坐标系的转换矩阵；α 和β 分别为攻角和侧滑角。

高喷防渗板墙布置在闸室基础中，立面呈矩型，全长65.6m，其顶部插入闸室底板中，底部伸入闸基下-10.0m，高程-12.2m。

由于引信波束为轴对称的空心圆锥，可以不考虑导弹滚动角的影响。

然后，将 导 弹 原 点 坐 标［xMn（t），yMn（t），zMn（t）］与引信坐标（xF，yF，zF）对应相加，即得引信运动轨迹［xFn（t），yFn（t），zFn（t）］，记 为 直 线lF（t）。

（2）计算目标特征点的运动轨迹

首先，建立目标特征点模型。在目标表面上取大量特征点近似模拟目标，当某一特征点的运动轨迹与引信波束相交时，认为引信探测到该特征点［8］。

反舰导弹类靶标外形通常近似为细长圆柱体，可简化为直杆。将尾部发动机火焰喷口作为目标机体坐标系原点，从原点开始向头部方向，选取各特征点Tj（j＝1，2，…，n），机体坐标分别记为（xTj，yTj，zTj），将（xTj，yTj，zTj）转换为地面坐标（xTj0，yTj0，zTj0），坐标变换与式（2）同理。由于反舰导弹类靶标结构上多为轴向对称，可不考虑滚动角的影响。计算目标航向角φT和目标飞行轨迹倾角θT的方法与计算φM和θM相同。

然后，将目 标 原 点 坐 标［xTn（t），yTn（t），zTn（t）］与特征点Tj坐标（xTj0，yTj0，zTj0）相加，即得特征点运动轨迹［xTjn（t），yTjn（t），zTjn（t）］，记为直线lTj（t）。

（3）计算引信启动参数

首先，计算引信启动角，记t时刻引信F和目标各特征点Tj之间的直线为lFTj（t），其方向数［mFTj（t），nFTj（t），kFTj（t）］为

直线lF（t）和直线lFTj（t）的夹角记 为ΩFTj（t）。已知直线lF（t）方向数为（vxM，vyM，vzM），则ΩFTj（t）表示为

然后，确定引信启动参数。引信启动时间tΩ由试验导弹遥测参数精确记录，则由ΩFTj（tΩ）＝Ω 对应的目标特征点（xTj，yTj，zTj）即为引信启动部位，引信到启动部位的距离即为引信启动距离R（tΩ）。

2 引信启动参数计算精度仿真

2.1 误差参数设置

引信启动部位和启动距离计算精度定义为误差影响下的计算值偏离其真值的1倍标准差，分别用σTj和σR表示。影响计算精度的误差因素主要包括：双站布设方案、经纬仪测角和事后判读误差、经纬仪采样周期、导弹攻角和侧滑角计算误差。

同测双站在弹目遭遇点的交会角在［60°，120°］范围内测量精度较高［9-10］，为此仿真时采用一种交会角约为90°的布站方案，双站与遭遇点的距离均约为20km。

设方位角和俯仰角测角精度σA＝σE，仿真时取10″、15″、20″。将判读精度σp折算为角度，取5″、10″。且设测角和判读随机误差为加法性误差。

由最小二乘拟合原理可知，光测采样周期T越小，则实际获取的同帧画幅数越多，弹目光测数据拟合精度越高。仿真时Ts取10ms、15ms、20 ms。

导弹攻角和侧滑角通常很难准确实时测量，但可以利用光测数据和导弹制导控制遥测参数计算得到粗略值。由于篇幅所限不再给出详细算法。导弹攻角和侧滑角范围一般为±10°，所以仿真时取2″、4″，且设攻角和侧滑角计算精度σα＝σβ。

2.2 启动参数计算精度仿真

在地面坐标系oxyz 下，设遭遇段弹目运动轨迹真值序列分别如式（7）和式（8）所示。

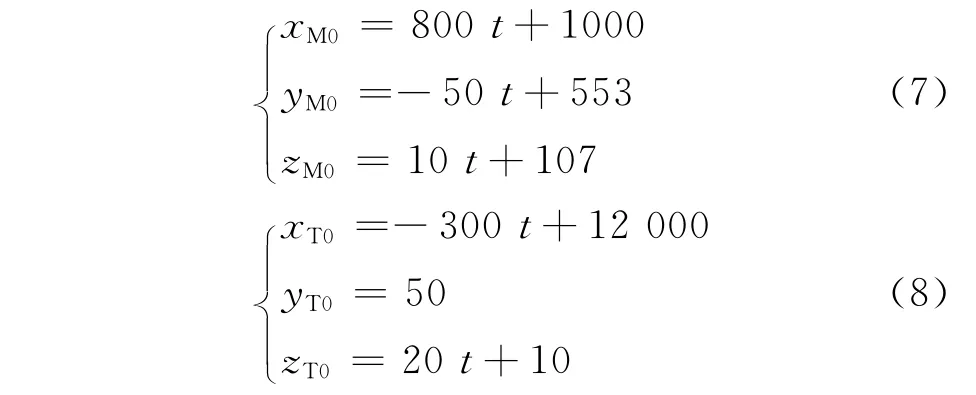
表1 光测误差影响下的引信启动部位计算精度

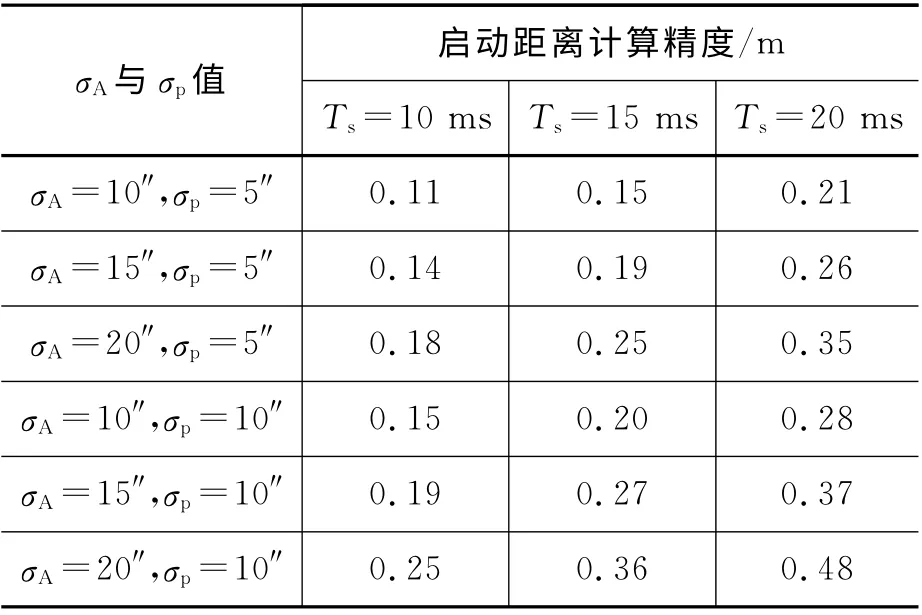
表2 光测误差影响下的引信启动距离计算精度

设引信弹体坐标为（2m，0，0），Ω＝60°，导弹攻角α 和侧滑角β 均为5°，目标攻角和侧滑角均为0°。经计算，引信启动时间为9.992s，启动距离为5m，启动部位的目标机体坐标为（4 m，0，0）。

设同帧画幅光测时间段为［9.800s，10.000 s］。采样周期、测角和判读误差、攻角和侧滑角计算误差取设定值，与弹目真值计算合成仿真光测数据。每次取值采用蒙特卡洛统计法仿真1 000次。设σα＝σβ＝0°，光测误差影响下的启动部位和启动距离计算精度仿真结果分别如表1和表2所示。

分析表1和表2，可得光测误差的影响：

a）测角误差、事后判读误差、采样周期对计算精度影响都很大，当判读精度αp为5″、测角精度σA不大于15″、采样周期TS小于15ms时，可以保证计算精度不大于0.2m；

b）启动部位计算精度σTj与启动距离计算精度σR相当，σTj仅略小于σR。

设T＝10 ms、σp＝5″，导弹攻角和侧滑角计算误差影响下的计算精度统计仿真结果如表3所示。

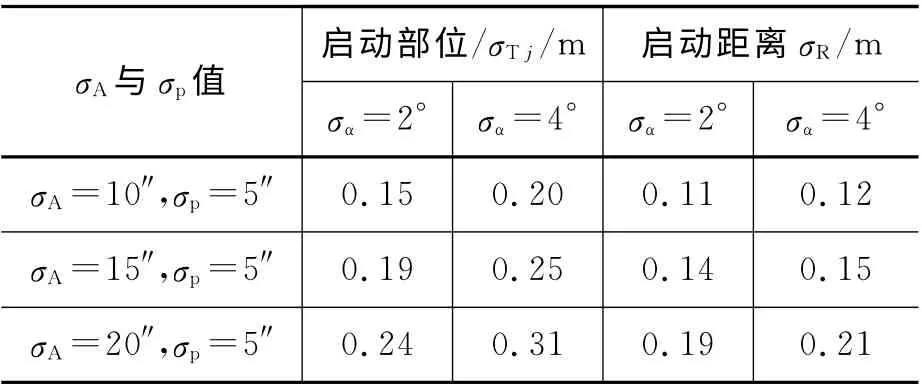
表3 导弹攻角和侧滑角计算误差影响下的引信启动参数计算精度

由表3可知，攻角和侧滑角计算误差对启动距离计算精度影响较小，而对启动部位计算精度的影响较大。这是因为由攻角和侧滑角计算误差引起的启动部位变化与启动距离成正弦关系，启动距离越大，启动部位变化越大。

3 结论

本文研究了舰空导弹飞行试验时窄波束侧视引信启动部位和启动距离的计算方法，并利用蒙特卡洛统计法仿真分析了相关测量因素对计算精度的影响。研究表明：启动参数计算方法正确；只要确保经纬仪测量和处理精度、减小采样周期，提高导弹攻角和侧滑角获取精度，就能达到启动参数计算精度要求，满足导弹试验结果分析与评估需要。

［1］ 李秋顺.光学测量处理脱靶量研究［J］.光子学报，1999，28（3）：255-259.

［2］ 杨璐，张军，裴喆.利用遭遇参数修正遥测与光测时统零点［J］.遥测遥控，2013，34（4）：70-74.

［3］ 刘利生.外弹道测量数据处理［M］.北京：国防工业出版社，2002：295-298，273，225-269.

［4］ 高策，乔彦峰.光电经纬仪测量误差的实时修正［J］.光学精密工程，2007，15（6）：846-851.

［5］ 柴敏，胡绍林，楼琳，等.光电经纬仪判读误差分析技术与应用［J］.飞行器测控学报，2006，25（1）：80-85.

［6］ 杨志群.导弹试验遥外测零点的分析与修正［J］.四川兵工学报，2014，35（3）：5-7.

［7］ 钱杏芳，林瑞雄，赵亚男.导弹飞行力学［M］.北京：北京理工大学出版社，2008：30-36.

［8］ 金光军，王朝志，陈万春.激光引信启动点的简化计算模型［J］.战术导弹技术，2008，（2）：67-70.

［9］ 石彦召，朱新华，郑百源，等.基于光电经纬仪的布站研究［J］.探测与控制学报，2009，31（增刊）：86-89.

［10］ 侯宏录，周德云.光电经纬仪异面交会测量及组网布站优化设计［J］.光子学 报，2008，37（5）：1023-1028.