红外图像改进非局部均值滤波算法研究

张 凡

(河南经贸职业学院信息管理系，郑州450018)

引 言

红外图像相对于一般的数字图像而言分辨率较低、图像中信息量较少，因此，该类图像在滤波过程中，应特别注意保持图像中信息的不丢失［1］。对此，HE等人［2］构建了一种基于曲波变换的红外图像去噪模型，对经过曲波变换后的图像系数，采用新的阈值函数进行处理，成功地去除了图像中的噪声;SHA等人［3］提出了一种改进型小波阈值函数模型，实现对红外图像中噪声的有效抑制;KANG等人［4］针对红外图像同时受到加性和乘性噪声的干扰，通过反复执行两次小波变换，去除了图像中的混合噪声;XIA等人［5］对经过小波变换后的图像系数采用最小二乘算法进行估计，对估计后的图像系数实现重构，从而有效地“过滤”了噪声;KANG等人［6］针对红外图像的噪声，结合图像自身统计特性，将小波去噪与自适应维纳滤波有机结合，实现对噪声图像的多级滤波。由此可见，变换域去噪是当前红外图像滤波的主流方法。该类方法尽管能够滤除图像中的一部分噪声，但图像的分解与重构过程非常耗时，无法胜任实时化要求较高的红外图像处理。与上述滤波思路不同的是，非局部均值滤波算法(nonlocal means filtering，NLMF)将图像中噪声点的滤波放到整幅图像中进行考虑，而非局限于有限的图像区域，通过充分挖掘图像中所有与噪声点区域相似的信息，使其全部参与到噪声点的滤波过程中去，使得滤波后的图像信息失真程度较小［7－9］。对此，本文中对该算法进行适当地改进，将其应用与去除红外图像中的噪声。

1 NLMF算法及其改进

1.1NLMF 算法

NLMF算法通过在整幅图像中寻找与该噪声点具有结构相似的像素区域，通过计算这些区域与噪声点所在图像块的欧氏距离，并将该距离值的负指数函数值作为权重，通过对各图像块的像素灰度值进行加权运算，从而获得噪声点的滤波值。对于一幅红外视频监控噪声图像(I表示图像的坐标域)而言，对于图中任一噪声点a，NLMF对该点的滤波结果为:式中，w(a，a')为权重值，其作用在于衡量图中像素点a'与噪声点a的相似程度，且w(a，a')∈［0，1］。

记像素点a'和a所在的图像局部方形区域灰度矩阵分别为Na'和Na，则该两点的相似程度决定于Na'和Na相似程度，Na'与Na的相似性可由两者灰度值向量的欧氏距离确定:

式中，φ(Na)，φ(Na')分别为 Na'与 Na灰度值向量。

经过(2)式计算后，图像中灰度值矩阵间欧氏距离越小，则说明两者相似度较高，那么在滤波时赋予较大的权重值，权重值计算公式为:

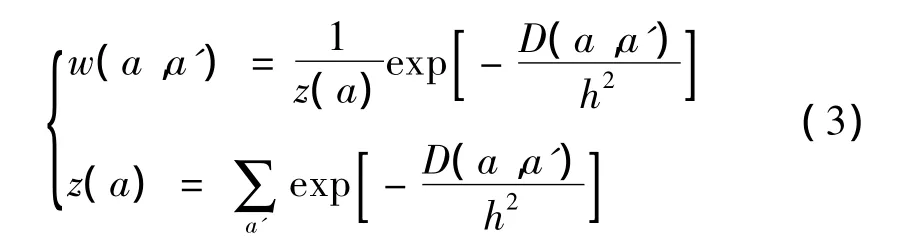
式中，h为调节因子，其作用在于控制权重值w(a，a')相对于D(a，a')的衰减程度。

1.2 改进NLMF算法

NLMF算法存在如下问题:(1)图像块一般设定为方形，对于获取图像中细节信息，如道路、河流、建筑物边缘等连续性信息时，会将一些无关的像素点囊括至图像块中，导致所获取的图像块间相似度不高;(2)图像块间的相似性主要是通过两者间的像素灰度值向量的欧氏距离来进行衡量，而对于图像中结构相似信息相似的区域，可能由于其与噪声点区域的欧氏距离较大，而被赋予较小的权重值，从而导致最终的滤波结构没有较好地顾及图像结构信息。因此，本文中尝试从以上两个方面对NLMF算法进行适当地改进。

1.2.1 基于灰度信息的相似图像块划分方法 该方法是通过将NLMF搜索区域内的像素点根据各自灰度值的相近程度，通过设定一定的阈值，来进行划分，在某种程度上实现相似像素点的动态聚类，从而有效划分出图像中的相似的图像块。使得划分出的相似图像块，不再局限于固定尺寸，而是随着像素点灰度值的实际分布情况，自适应地调整图像块的形状和尺寸。为了便于论述，将噪声图像的搜索区域尺寸简化为9×9，相似图像块提取具体步骤如下。

步骤1:统计搜索区域内所有像素灰度均值。

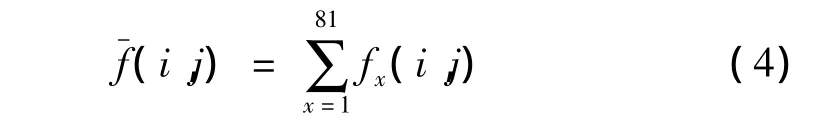
式中，fx(i，j)为区域内任意一点灰度值。

步骤2:记(i，j)为阈值A，将区域内所有像素点灰度值与该阈值进行比较，将小于该阈值的区域像素点记为目标信息点(记为子区域Ω1);大于该区域的区域像素点记为背景信息点(记为子区域Ω2)。

步骤3:若Ω1中，存在孤立的像素点，那么保持该类该类像素点不变，各自作为一个图像块存在;若存在2个获以上的像素点“聚集”区(记为子区域Ω1-1)，那么，将该类区域中像素点灰度值组成集合Q:

式中，fn(i，j)为区域Ω1-1中的任一像素点灰度值。统计集合Q中的灰度中值:

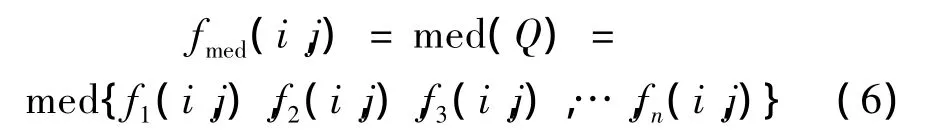
式中，med(·)为取中值运算。将fmed(i，j)记为阈值AΩ1-1，对Ω1-1中的像素点进行进一步划分。

步骤4:参照步骤3对Ω2进行处理，完成对该区域内像素点的划分。

步骤5:重复执行步骤1～步骤4，完成整幅图像相似图像块的划分。

1.2.2 滤波权重值计算方法 NLMF算法仅通过衡量图像块间欧氏距离的大小来作为衡量其余待滤波像素点的相近程度，如果距离较大，则相近程度较小，从而导致距离待滤波点的图像信息在滤波过程中比较少或者不考虑，这对于细节信息丰富的红外图像而言，处滤波效果不佳。结构相似度(structural similarity，SSIM)将图像中的亮度、结构、对比度等信息进行有效结合，对图像质量进行整体评价，可通过下式评价以像素点a和a'为中心的图像块的相似性:

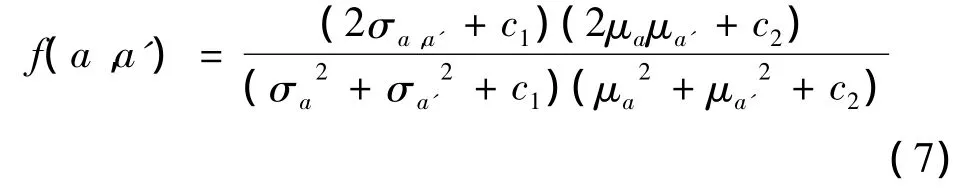
此时，图像块间相近程度越高，s(a，a')越小，且s(a，a')∈［0，1］，其单调性与(2)式保持一致。将(2)式与(8)式相结合，从而有:

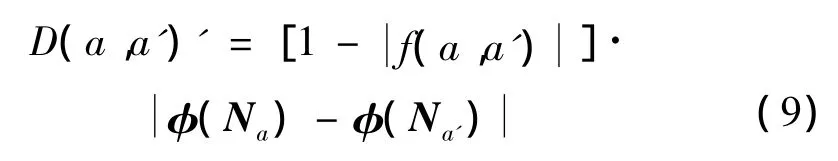
将(9)式代入(3)式，则新的权重计算公式为:

2 实验结果与分析

本文中选取随机拍摄的两幅红外图像，分别采用NLMF算法(算法1)、两种改进NLMF算法(算法2［8］、算法3［9］)与本文中的INLMF算法(算法4)进行滤波效果比较分析，结果分别见图1、图2。对算法1～算法4滤波结果分别采用峰值信噪比(peak signal－tonoise ratio，PSNR)［10］和结构相似度指标(SSIM)［11］进行客观的评价，结果分别见表1和表2。

Fig.1 Comparison of the filtering results of the first infrared image

Fig.2 Comparison of the filtering results of the second infrared image

由图1和图2可知，经典NLMF算法对于受到该水平高斯噪声污染的红外图像滤波效果不理想，尽管滤除了图像中的一部分噪声，图像中的人物信息仍无法辨认(见图2b左侧”人物”，“道路边缘”)。参考文献［10］中提出的改进型NLMF算法滤波结果分别如图1d和图2d所示，相对于前者，图像中的噪声抑制程度有所提高，这是因为该算法中，加入了高斯滤波环节，使得改进后的NLMF算法噪声抑制能力有了一定程度的提升。参考文献［11］中提出的基于K均值聚类的改进NLMF算法去噪结果分别见图1e和图2e，该算法通过采用K聚类算法实现对图像中信息的预先分类，在此基础上进行滤波，从整体上看，该算法的去噪效果与参考文献［10］中算法较为相近。INLMF算法去噪结果如图1f和图2f所示，图中“人物、道路、汽车”等信息基本从噪声中恢复出来，且图中的残留噪声较少，在清晰度方面，与各自的原始图像(见图1a和图2a)最为接近。由表1和表2可知，INLMF算法PSNR和SSIM值最高，说明该算法能够有效去除红外图像中的噪声，其滤波性能不但优于经典NLMF算法，而且相对于两类已有的改进型NLMF算法而言，也具有一定的优势。

Table 1 Quantitative evaluation results of the filtering results of the first infrared image

Table 2 Quantitative evaluation results of the filtering results of the second infrared image

3 结论

针对红外噪声图像，提出了一种改进型非局部均值滤波算法(INLMF)，该算法分别从相似图像块划分和权重计算方法两个方面对经典NLMF算法进行了改进。实验结果表明，INLMF算法对于红外噪声图像去噪效果较好。

［1］ YU W J，GU G H，YANG W.Fusion algorithm of infrared polarization images based on wavelet transform［J］.Laser Technology，2013，37(3):289－292(in Chinese).

［2］ HE Y J，LI M，LÜ D，et al.Novel infrared image denoising method based on Curvelet transform［J］.Computer Engineering and Applications，2011，47(32):191－193(in Chinese).

［3］ SHA J M，LIU Z Q，PANG Sh，et al.The application of an improved wavelet threshold algorithm in infrared image denoising［J］.Journal of Projectiles Rockets Missiles and Guidance，2012，32(3):35－38(in Chinese).

［4］ KANG Zh L，XU L J.An algorithm study on infrared image denoising based on wavelet transform［J］.Computer Simulation，2011，28(1):265－267(in Chinese).

［5］ XIA D F，LUO D Sh，LU J Zh，et al.Wavelet adaptive denoising method for faulty insulators infrared thermal image based on total least squares estimation［J］.Computer Engineering and Applications，2012，48(25):198－202(in Chinese).

［6］ KANG Ch Q，CAO W P，HUA L，et al.Infrared image denoising algorithm via two－stage 3－D filtering［J］.Laser ＆ Infrared，2013，43(3):261－264(in Chinese).

［7］ SHREYAMSHA KUMAR B K.Image denoising based on non－local means filter and its method noise thresholding［J］.Signal，Image and Video Processing，2013，7(6):1211－1227.

［8］ ZHANG L G.Fast non－local mean for image denoising［J］.Singal Processing，2013，29(8):1043－1049(in Chinese).

［9］ QIAO Z L，DU H M.NL means algorithm based on K－means clustering for ultrasound image denoising［J］.Computer Engineering and Design，2014，35(3):939－942(in Chinese).

［10］ WANG X B，SUN J Y，TANG H Y.Adaptive filtering algorithm for mixed noise image based on wavelet transform［J］.Microelectronics＆ Computer，2012，29(6):91－95(in Chinese).

［11］ ZUO P，WANG Y，SHEN Y Ch.Image denoising algorithm based on wavelet packet transform and total variation model［J］.Journal of Jilin Unversity(Science Edition)，2014，52(1):81－85(in Chinese).