基于BP网络的面曝光成形系统制作参数优化研究*

□ 巨孔亮 □ 胥光申

西安工程大学机电工程学院 西安 710048

快速成形技术的工业化应用推广，必须解决制作精度这一关键问题，同时，制作精度也是面曝光快速成形技术研究的重点。面曝光快速成形系统制作工艺参数影响着制件的制作精度，不合理的制作参数组合会降低制件的形位精度，或者在保证制件可固化的前提下，延长制作时间，降低制作效率，而针对小尺寸制件，严重时会产生较大的翘曲变形[1]。因此，为了提高曝光平面内制件的制作精度，必须对曝光平面内的制作工艺参数进行优化研究。

近年来，为了提高光固化快速成形制件的制作精度与质量，许多国内外学者将扫描间距、过固化深度、涂层时间、分层厚度及刮刀间隙作为主要影响因素，以提高制件的尺寸精度为目标，进行工艺优化。其中，G Weheba等[2]将固化深度、过固化深度及Z向等待时间作为控制因子，以制件的尺寸精度、平整度及表面粗糙度为目标，采用Box-Behnken试验设计方法对光固化快速成形工艺进行优化；Shih-Hsuan Chiu等[3]将固化时间、等待时间、浸没深度、光通量及工作台移动速度作为可控变量，采用一种基于中心组合设计的响应曲面的方法，以提高制件的尺寸重复性精度为目标，进行工艺参数优化；Schaub D A等[4]考虑了层厚、过固化深度、制件方向及光斑重叠率4个因素，以制件尺寸精度、强度与表面粗糙度为目标，进行工艺优化；胥光申等[5]将扫描间距、扫描速度、线宽补偿以及树脂收缩补偿因数作为控制因素，并考虑扫描速度与另外三个因素之间的交互作用对制件精度的影响；文献[6]将辐照度、曝光时间间隔、曝光时间与面收缩补偿因数作为影响制作精度的主要因素，运用田口方法，对参数进行优化组合，从而提高制件的制作精度。与前人相比，笔者针对40 mm×30 mm图幅大小的成形系统，将面收缩补偿因数、曝光时间间隔、曝光时间、辐照度、双向交错曝光宽度及交错曝光时间间隔作为主要控制因素，以制件的制作精度作为优化目标，采用BP神经网络方法，对各主要因素进行优化，确定出最佳的工艺制作参数组合，为制作高精度制件奠定了坚实的基础。

1 样本数据的获取

1.1 试验因素

影响面曝光快速成形系统水平面内制件制作精度的主要因素，分别是面收缩补偿因数、曝光时间间隔、曝光时间、辐照度、双向交错曝光宽度及交错曝光时间间隔，将这6个因素作为控制对象，每个因素各取4个水平。表1列出了每个因素在不同水平时的取值。

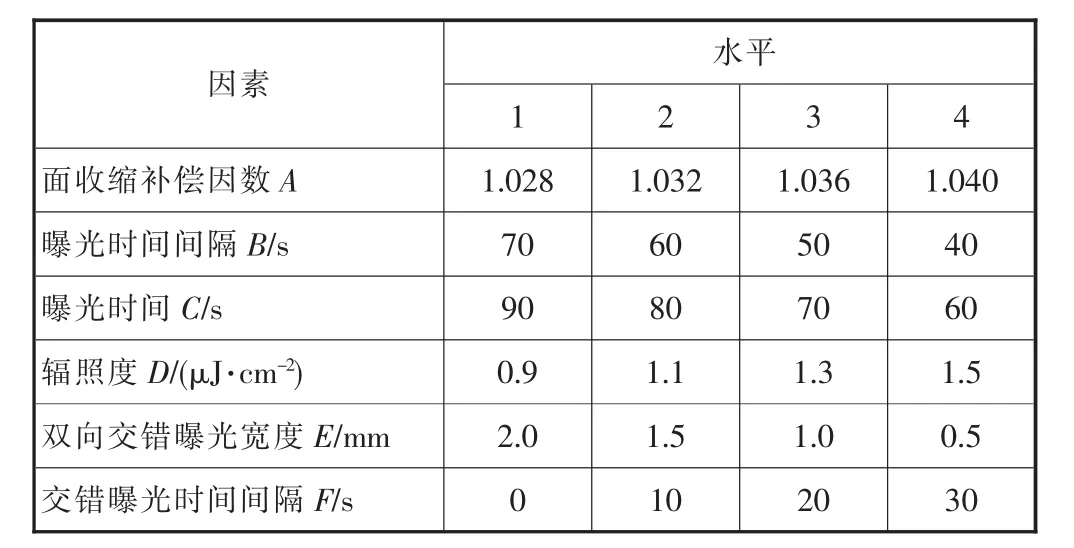
表1 因素水平表

1.2 利用正交试验获取样本

正交试验法[7]是利用正交性原理与数理统计学来合理安排多因素试验的一种科学方法。采用该方法可减少试验次数，提高试验制作效率，并且能够迅速确定出最佳的试验方案。为了获取较多的样本数据点，笔者采用自由度为64的L64（421）型正交表，表头设计见表2，其中，第n列为每个因素所对应的正交表列号。

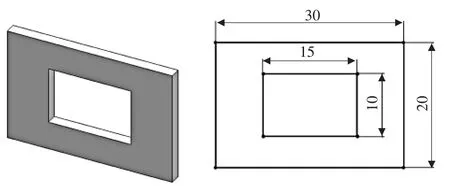
▲图1 测试件的三维模型与尺寸/mm

▲图2 部分测试件

为了获取BP网络训练所需的样本数据，利用自主开发的面曝光快速成形系统，选用aidi-UV2230型光敏树脂为成形材料，针对40 mm×30 mm大小的图幅，按照L64（421）型正交表，在64组不同制作条件下，制作如图1所示的测试件。为了保证试验结果的可靠性，每个测试件制作2个，制作结束后，经酒精清洗及后固化处理，得到如图2所示的测试件，在小型工具显微镜下测量测试件的实际外长宽及内长宽尺寸。每个测试件的长宽尺寸分别测量3次，取平均值作为实际尺寸，将两组试验的理论尺寸与实际尺寸相减得到相应的误差，作为网络的输出变量。而网络的输入为6个因素按照试验计划取不同水平时所对应的试验设定值，结果见表2。

2 基于BP神经网络的制作参数优化

2.1 BP神经网络

BP（Back Propagation）网络[8]是一种多层前馈神经网络，它能够建立输入与输出间的任意非线性映射，利用反向传播学习算法来调整网络的权值。笔者采用三层的前馈神经网络，对面曝光快速成形系统制作参数进行优化研究。如图3所示，该网络结构一共有3层，分别是输入层、隐层与输出层。其中，隐层与输出层的神经元分别采用非线性阈值函数tansig和线性函数purelin作为激励函数。以面收缩补偿因数A、曝光时间间隔B、曝光时间C、辐照度D、双向交错曝光宽度E及交错曝光时间间隔F作为网络的输入变量，而将试验所测量的理论尺寸与实际尺寸相减得到的误差作为网络的输出变量，建立BP神经网络模型。

2.2 网络的训练

获取样本数据后，首先对表2中的样本数据进行归一化处理，将处理后的结果作为网络的实际输入与输出，同时，网络训练的目标均方差设定为0.01 μm，最大迭代次数设定为1 000，权值和阈值的初始值在[0，1]范围内随机选取[9]。 其次，根据算式（1）计算出网络结构所需要的隐层单元数，再利用trainlm函数对网络进行多次训练，得到6-12-4的网络结构，即隐层单元数为12时，均方差最小，结果见表3。

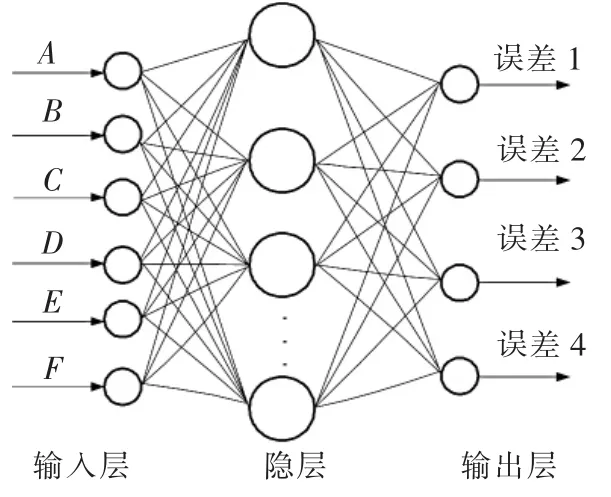
▲图3 BP神经网络模型

式中：n1为隐层单元数；n为输入层神经元数目；m为输出层神经元数目；a为区间[1，10]内的常数。

最后，利用6-12-4的网络结构进行网络训练，得到网络训练误差结果，如图4所示。从图中可以看出，当最大迭代次数为33时，均方差小于0.01 μm，满足BP神经网络训练的要求。

2.3 参数优化的结果

网络训练结束后，得到网络的输出值，再通过MATLAB计算得到网络输出值与网络目标输出值之间的误差值，并且根据算式（2）计算出均方差（RMSE）。表4给出了均方差最小的一组，即正交设计表中编号为38的试验，它的参数组合最佳，其最佳组合是：A3B2C2D1E4F3。

计算隐层单元数：

式中：ei为网络输出值与网络目标输出值之间的误差值，n 取 4。

3 验证性试验

为了证明最佳参数组合的合理性，进行了试验验证。表5列出了非最佳参数组合条件下与最佳参数组合条件下所对应的尺寸误差。表5表明，在非最佳参数组合（A1B3C1D3E4F2）的制作条件下，误差最大可以达到320 μm，而最佳参数组合下的误差在80 μm之内。试验结果表明，选择合理的参数组合，才能够提高制件的制作精度。

表4 网络输出与目标输出之间的误差及均方差（部分）/μm

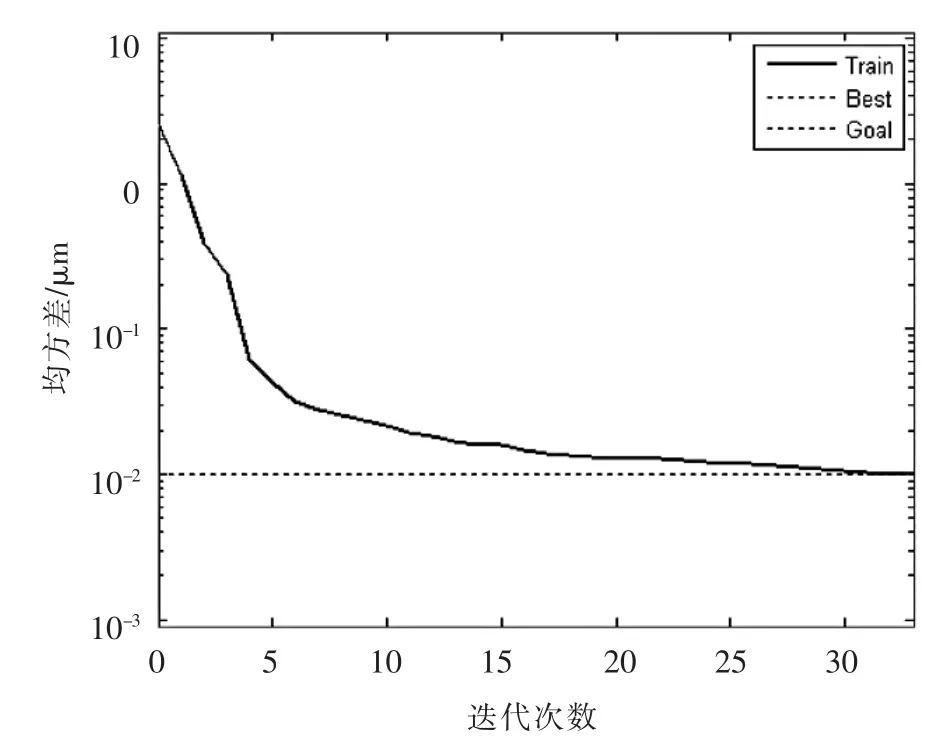
▲图4 网络训练误差结果

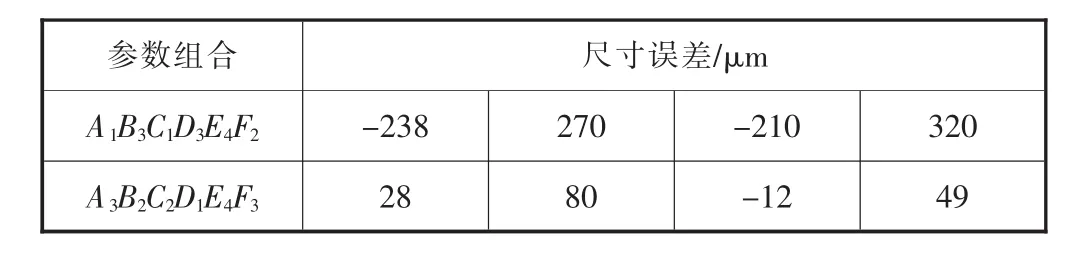
表5 验证试验结果

4 结论

对面曝光快速成形系统曝光面内的制作参数进行工艺优化，利用BP神经网络方法，确定了最佳制作参数组合。通过验证性试验表明，在非最佳参数组合的制作条件下，误差最大可以达到320 μm，而最佳制作参数组合下的误差在80 μm之内，明显提高了制件的制作精度。

[1]宫静，胥光申.面曝光快速成形技术的变形 [J].纺织高校基础科学学报，2011，24（4）：585-589.

[2]G Weheba ，A Sanchez-Marsa.Using Response Surface Methodology to Optimize the Stereolithography Process[J]．Rapid Prototyping Journal，2006，12（2）：72-77.

[3]Shih-Hsuan Chiu， Kun-Ting Chen， Sigit Tri Wicaksono，et al.Process Parameters Optimization for Area-forming Rapid Prototyping System [J].Rapid Prototyping Journal，2015，21（1 ）：70-78.

[4]Schaub D A，Montgomery D C.Using Experimental Design to Optimize the Stereolithography Process [J]. Quality Engineering，1997， 9 （4）：575.

[5]胥光申，赵万华，卢秉恒.高分辨率快速成形系统的光固化实验研究[J].西安交通大学学报， 2005（1）：66-69.

[6]Xu Guangshen，Yang Gen， Gong Jing．Optimizing Build Parameters for Integral Stereolithography System [J]．Advanced Materials Research，2012， 424-425：52-55．

[7]马成良，张海军，李素平.现代试验设计优化方法及应用[M].郑州：郑州大学出版社，2007.

[8]董长虹.MATLAB神经网络与应用（第二版）[M].北京：国防工业出版社，2007.

[9]巨孔亮，胥光申，王亚宁，等.基于BP神经网络的面曝光快速成形系统掩模图像的畸变校正研究 [J].机械制造，2013，51（11）：37-40.