考虑摩擦接触的沥青路面坑槽补缝处力学响应研究*

张 倩 李 泽 温志广 杨永红

(西安建筑科技大学土木工程学院1) 西安 710055) (包头市交通运输局2) 包头 014030)

考虑摩擦接触的沥青路面坑槽补缝处力学响应研究*

张 倩1)李 泽1)温志广2)杨永红2)

(西安建筑科技大学土木工程学院1)西安 710055) (包头市交通运输局2)包头 014030)

为了给沥青路面坑槽结构修补设计提供科学的理论支持，针对坑槽补缝处力学响应的影响因素修补厚度和修补料与原路面材料的模量比，采用Goodman零厚度单元模型，运用非线性有限元软件ABAQUS计算了不同修补厚度、不同模量比与荷载耦合作用下补缝处的力学响应，分析了补缝处力学指标随接触摩擦系数的变化规律.研究结果表明：不同接触模型对补缝最大拉应力和最大剪应力计算结果影响较大；不同修补厚度和模量比条件下，横缝最大拉应力无显著变化；而纵缝处，一定修补厚度和模量比条件下最大拉应力出现峰值，且由顶部到底部呈先减小后增大趋势，各补缝处最大剪应力关系是纵缝顶部>补块表面>橫缝底部，模量比为0.5时出现峰值0.32 MPa.

道路工程；接触摩擦系数；Goodman模型；模量比；修补厚度；坑槽修补；力学响应

0 引 言

坑槽修补一直是沥青路面养护维修工作的难点之一，工程实践表明，修补边界是坑槽修补块的最薄弱部位，破损往往从补缝结合面出现.修补料与原路面材料间的结合状态通常既非完全连续也非完全光滑，而是处于这2种极端状态之间，即所谓的半结合状态[1]，以往分析中采用完全连续的理想状态与补缝实际工作状态不符.

文献[2-6]分析了弹性模量及修补厚度等因素对坑槽补缝的力学影响，但都建立在路面结构完全连续的基础上.文献[7]对坑槽修补结构进行了力学研究分析，表明修补材料模量对修补结构力学性能影响显著，但未考虑修补厚度的影响.文献[8]研究表明不同结构层层间接触状态对路面结构力学响应影响很大，但却忽略了修补块材料模量的影响.水平荷载易引起路面剪切变形和修补块破坏，而已有坑槽修补力学研究[9-10]只采用竖向荷载，没有考虑水平荷载对路面的影响，实际上水平剪应力也是导致修补边界失效的重要原因之一.本文运用具有良好接触分析性能的有限元软件ABAQUS进行仿真，计算了坑槽在不同修补厚度、不同模量比与荷载耦合作用下的力学响应，研究了各响应指标随坑槽补缝接触状态变化的规律，解释了考虑修补厚度及模量比时，补缝在不同接触状态下的破坏机理，为坑槽修补材料和结构设计提供依据.

1 模型建立及参数设置

1.1 界面接触模型

为模拟补缝界面接触状态，采用更符合坑槽补缝界面工况的Goodman等[11]提出的零厚度接触面单元模型.

1.2 结构模型及参数

路面结构层由面层、坑槽修补块、基层、底基层及土基构成，各结构层及其材料参数根据某工程设置，见表1.

表1 路面各结构层参数

计算采用标准轴载BZZ-100，轮胎接地压强0.7 MPa.实际轮胎与路面的接地形状并非简单的圆形均布荷载，而更接近于矩形，为便于计算，将轮载简化为正方形均布荷载189 cm×189 cm，接地面积357.21 cm2，双轮中心距为31.9 cm，水平荷载为竖向荷载的一半，即水平力系数取0.5[12]，荷载作用如图1b)所示.补块与原路面材料模量比ζ分别为0.5，1.0，1.7，2.0，3.3，5.8，8.3.坑槽纵、横缝和底面与原路面的接触均采用理想的完全连续状态(用Cont表示)和符合实况的摩擦接触状态，补缝接触状态以摩擦系数μ来表征，其值分别取0，0.2，0.4，0.6，0.8，1.0，其余各结构层接触状态以完全连续定义.

图1 有限元模型示意图

1.3 有限元结构模型及参数

考虑建模分析精度和计算时效性，确定模型几何尺寸为4 m×4 m×4.5 m，补块几何尺寸为1 m×1 m×(0.04，0.06，0.09)m，计算模型如图1所示.为减小计算冗余程度，提高精时比(数据精度与计算所耗时间的比值)，将补块单元网格加密细分为0.05×0.05×h，原路面结构单元划分为0.1×0.1×h，采用线性减缩积分六面体单元C3D8R.

2 计算结果及分析

2.1 修补厚度对补缝处力学响应的影响

分别选取修补厚度为4，6和9 cm 3种工况进行力学响应分析，以便于在工程中根据坑槽破坏程度合理确定修补厚度.

2.1.1 纵、横补缝最大拉应力 修补厚度影响补缝处的拉应力，而拉应力是补缝处发生拉裂破损的主要因素，拉应力愈大，补缝粘结恶化愈严重，最大拉应力计算结果如图2.

由图2可知：(1)与连续接触模型相比，采用摩擦接触模型时各补缝最大拉应力显著增大，μ=1.0时的最大拉应力是连续状态下的5倍左右.坑槽修补的层次性及材料的差异性决定了其边界为不连续接触状态，以更合理的摩擦接触模型对其进行力学分析，才更具指导意义；(2)不同修补厚度下，横缝处最大拉应力无明显变化；但随修补厚度加深，纵缝处最大拉应力由顶部到底部先减小后增大，最大值0.32 MPa出现在修补厚度为4 cm时顶部，分别约为修补厚度为6 cm纵缝顶部、4 cm橫缝底部和9 cm纵缝底部的1.2，2.1和3.1倍，表明补缝拉裂更易出现在修补厚度较薄的纵缝顶部；(3)当补缝接触状态较好(μ≥0.8)时，修补厚度对最大拉应力影响较小；但当μ<0.8时，各补缝处最大拉应力随μ减小呈非线性递增趋势；修补厚度为4，6和9 cm时，其最大拉应力最大增幅分别达到了51%,50%和38%.

2.1.2 纵缝及底面补缝最大剪应力 剪切变形与剪应力密切相关，坑槽补缝处的最大剪应力受修补厚度及水平荷载影响较大，计算结果如图3.

图3表明：(1)不同修补厚度下，各补缝处最大剪应力关系是：纵缝顶部>补块表面>橫缝底部，且纵缝顶部最大剪应力峰值达到0.29 MPa，荷载对纵缝处剪切破坏最显著；(2)随接触状态的恶化，纵缝最大剪应力先增大后减小，修补厚度为4 cm时，其最大降幅达38%左右；(3)当修补厚度为9 cm时，两种接触状态对底面补缝处最大剪应力影响甚微，原因是水平荷载的施加导致最大剪应力由面层底向上移动，间接加强了层底补缝粘结能力；当修补厚度为4 cm时，其最大剪应力变化较大，可见修补厚度太薄时补缝抗剪不利.

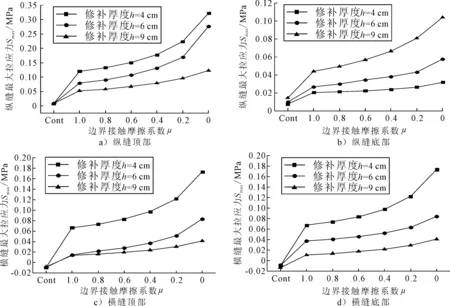
图2 不同修补厚度下各补缝处最大拉应力

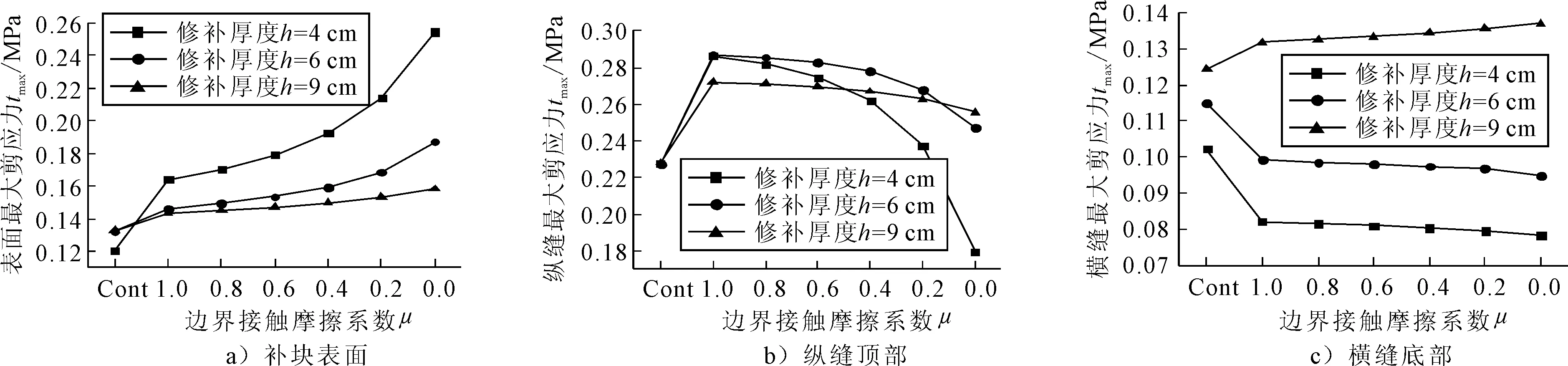
图3 不同修补厚度下各补缝处最大剪应力

2.2 模量比对补缝处力学响应的影响

补块与原路面材料的模量比过小或过大都会导致补缝处产生较大应力集中，计算中模量比以梯度变化，按最不利原则提取应力，得到3种修补厚度时的最大应力，以指导在修补设计中能根据坑槽修补厚度确定较合理的模量比.

2.2.1 纵、横补缝最大拉应力 模量比反映补块与原路面材料模量的差异，其值变动愈大，补缝处拉应力突变愈严重，见图4.

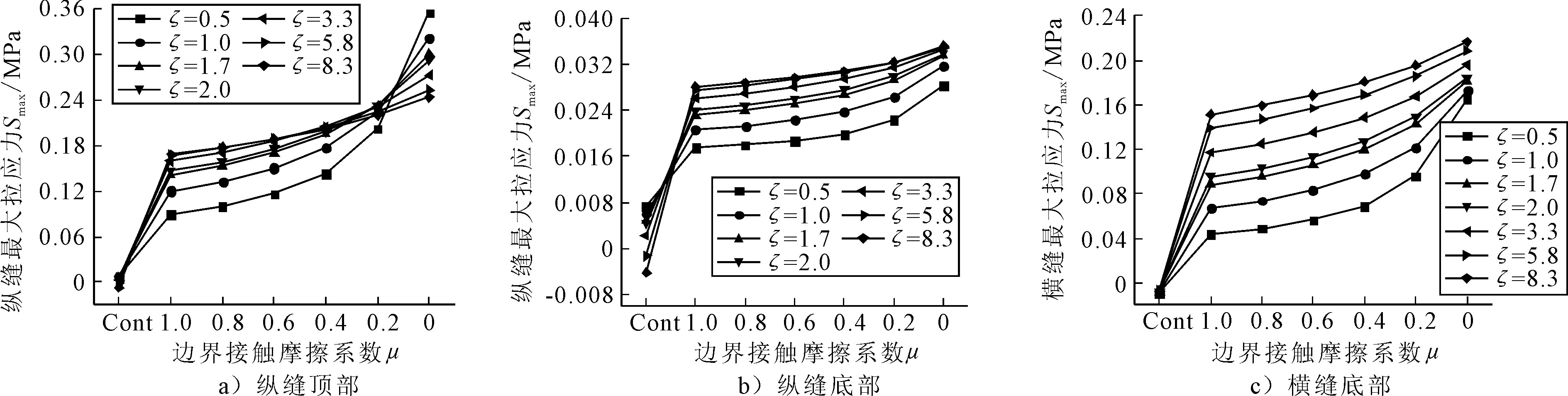
图4 不同模量比下各补缝处最大拉应力

由图4可见：(1) 采用连续接触模型与摩擦接触模型对补缝最大拉应力的计算结果影响较大，从连续模型到接触模型(μ=1.0)变化时，模量比ζ=8.3最大拉应力变化范围是ζ=0.5的2～4倍左右；当μ<1.0时，补缝处最大拉应力随模量比的增加呈非线性递增趋势；(2)各补缝最大拉应力对不同模量比的敏感性有较大差异，模量比越小；敏感性越高，反之，亦然；(3)纵缝顶部拉应力最大，尤其当ζ≤1.0时飙升至最大值0.35 MPa，已接近材料的抗拉拔强度0.36 MPa，考虑到模量比对补缝最大拉应力影响显著，在工程中要合理选择具备足够强度和刚度的修补料和粘结料.

2.2.2 纵缝及底面补缝最大剪应力 模量比变化反映补缝处材料刚度分布，修补块刚度变化对坑槽补缝处剪切破坏影响较大，计算结果如图5.

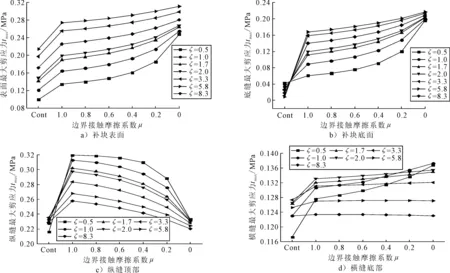
图5 不同模量比下各补缝处最大剪应力

图5计算结果表明：(1)在摩擦接触条件下，模量比分别为ζ=0.5和ζ=8.3时，补缝处有最大剪应力0.32 MPa，可见模量比过小或过大均可引起修补料与原路面材料性能不匹配而使补缝处应力过于集中；(2)随模量比增大，表面和底面最大剪应力呈递增趋势，且其浮动范围在0.25～0.30 MPa和0.19～0.21 MPa之间，可见模量比较大的补块表面是承受最大剪应力的最不利区域；(3)当模量比ζ≤1.0时，补缝处最大剪应力随接触摩擦系数变化显著；在橫缝底部，随模量比增大，最大剪应力呈先增大后减小趋势，最终在两种接触状态下基本趋于一致.

3 结 论

1) 不同修补厚度和模量比条件下，横缝最大拉应力无显著变化；但在纵缝处，当修补厚度为4 cm和模量比为0.5时最大拉应力出现峰值，且由顶部到底部呈先减小后增大趋势，说明坑槽更易在修补厚度较薄的补缝顶部发生拉裂破损，补缝接触状态对最大拉应力影响显著.

2) 补块表面最大剪应力与修补厚度和模量比分别呈负相关和正相关关系，在修补厚度为4 cm和模量比为0.5时最大剪应力变化幅度最大，其峰值已处于重交沥青混合料抗剪强度值域区间.

3) 最大剪应力均发生在纵缝顶部，对于不同的修补厚度和模量比，接触摩擦系数对橫缝最大剪应力影响不明显，相反，对纵缝最大剪应力影响较大.

4) 在坑槽修补设计时合理采用边界修补料和粘结料，加强对受力最不利补缝处的施工控制，可降低坑槽等病害复发的可能性，改善养护效果.

[1]王 凯．层状弹性体系的力学分析与计算[M]．北京：科学出版社，2009．

[2]延丽丽．基于ANSYS的沥青路面坑槽修补结构仿真分析[D]．西安：长安大学，2013.

[3]徐清华．沥青路面坑槽修补技术及其计算机仿真分析[D]．西安：长安大学，2009．

[4]郑木莲，王松根，陈拴发．耐久性沥青路面混凝土基层荷载应力的数值计算[J]．中国公路学报，2008，21(2)：28-33．

[5]李 杰，仲 甡，胡小弟．实测轮载接地压力的沥青路面车辙贡献率研究[J]．华中科技大学学报:自然科学版，2014，42(3)：102-106．

[6]董泽蛟，刘美丽，郑 好，等．考虑横观各向同性特性的沥青路面动力学分析[J]．中国公路学报，2012，25(5)：18-23.

[7]田耀刚，延丽丽，陈长征．材料模量对沥青路面坑槽修补结构力学性能影响分析[J]．武汉理工大学学报，2013，35(11)：58-61．

[8]刘红坡，邱 延．基于层间状态的沥青路面结构响应分析[J]．路基工程，2008(1)：34-35．

[9]李炜光，经冠举，田智仁．基于不同工艺沥青路面坑槽修补结构受力分析[J]．武汉理工大学学报:交通科学与工程版，2013，37(1)：19-22．

[10]KRUNTCHEVA M R,COLLOP A C,THOM N N. Effect of bond condition on flexible pavement performance[J].Journal of Transportation Engineering ASCE,2005，131(11):880-888.

[11]MAYER M H,GAUL L.Segment-to-segment contact elements for modeling joint interfaces infinite element analysis[J].Mechanical Systems and Signal Processing,2007,21(2):724-734.

[12]林绣贤．关于沥青混凝土路面设计中抗剪指标的建议[J]．公路，2004(12)：66-69．

Study on the Mechanical Response of Asphalt Pavement Potholes Considering the Frictional Contact in the Joints

ZHANG Qian1)LI Ze1)WEN Zhiguang2)YANG Yonghong2)

(SchoolofCivilEngineering，Xi`anUniversityofArchitectureandTechnology，Xi`an710055，China)1)(BaotouTrafficandTransportation，Baotou014030，China)2)

This paper aims at providing more scientifically theoretical support for repairing design of asphalt pavement potholes. Repairing depth and the modulus ratio between repair material and the original pavement material are two important factors affecting mechanical response in pothole joints. In order to unveil the relationship between the mechanical properties and contact friction coefficients at the joints, Goodman element model of zero thickness in nonlinear finite element software ABAQUS is introduced to simulate mechanical response under different repairing thickness, different modulus ratio and load combination. It is found that contact model has a great impact on the calculation results of the maximum tensile stresses and the maximum shear stresses at joints. The maximum tensile stress of transverse joints does not change greatly under different repairing thickness and modulus ratio conditions in each contact model. But for longitudinal joints, tensile stress exhibits a peak value. It first decreases and then increases from top to bottom of the joint. Shear stress shows a peak value at the top of longitudinal joints and the lowest value at the bottom of transverse joints. It reaches its highest value, 0.32MPa, when the modulus ratio is 0.5. The mechanical analysis results can guide the selection of repairing material and the design of pothole fill.

road engineering; contact friction coefficient; Goodman model; modulus ratio; repairing thickness; pothole fill; mechanical response

2015-03-20

*内蒙古自治区交通运输科技项目(批准号：NJ-2014-23)、河北省交通科技项目(批准号：Y-2010090)、陕西省教育厅专项科研计划项目(批准号：12JK0795)资助

U416.217

10.3963/j.issn.2095-3844.2015.03.013

张 倩(1971- ):女，博士，副教授，主要研领域为新型路面材料、路面病害机理与防治