基于动态规划和贪婪算法的停车楼智能停车优化方法*
2015-04-19徐良杰姚裔虎王冠云
赵 玮 徐良杰 姚裔虎 王冠云 李 革
(武汉理工大学交通学院1) 武汉 430063) (内蒙古科技大学经济与管理学院2) 包头 014010)
基于动态规划和贪婪算法的停车楼智能停车优化方法*
赵 玮1,2)徐良杰1)姚裔虎1)王冠云1)李 革2)
(武汉理工大学交通学院1)武汉 430063) (内蒙古科技大学经济与管理学院2)包头 014010)
针对各种类型的立体停车楼停车管理系统混乱、无序导致泊车及出车过程费时并易引起停车楼通道阻塞等问题,根据停车楼布局、历史停车数据库及待停车辆的信息,建立了二维背包模型,并将动态规划算法和贪婪算法相融合,提出启发式组合算法,使每一待停车辆进入停车场时即获取泊车位指示以便有序停靠,优化空闲停车资源分配,减少车辆在停车楼内停留总时间和通道阻塞,提高停车楼利用率.
停车楼;贪婪算法;动态规划算法;二维背包问题
0 引 言
我国针对多层停车楼的研究起步较晚,研究成果较少,已有的理论研究成果基本也是借鉴国外的现有成果和实践经验,根据我国停车楼实际情况所做的相关文献很少,文献[1]对停车需求特点和停车管理方式做了系统地介绍,但只定性分析了多层停车楼出现的必要性和作用;文献[2]以实例定量地证明了多层停车楼的发展前景及经济形势都十分乐观;文献[3]提出了人口密集城市和经济发达地区停车模式的发展方向应以机械式立体停车库和自走式停车库结合;文献[4] 采用静态优化方法待停车辆的信息不完整的情况下来探讨一种快速动态停车算法和模型,并且通过仿真模型验证.文献[5]侧重研究自动停车控制系统的实用性,建立基于激光雷达的自动泊车系统并应用于 DARPA 城市挑战赛.文献[6]提出了适用于任何停车场结构,以停车用时最短为目标函数的快速自动停车算法,通过计算机程序实现并进行了验证.本文以动态规划算法和贪婪算法的混合算法解决二维背包问题,考虑了每辆车的进入或驶出后整体停车位状态变化,寻求周期性的整体最优解,最后通过软件实现多层停车楼智能停车优化.
1 模型建立
1.1 建模基本假设
为简化背包问题,作如下假设:(1)停车楼每层可停车空间为矩形,不考虑转弯处的较小奇异型空间、楼内承重柱体面积、护栏厚度、电梯占用空间等;(2)停车位的规格可以容纳各种类型的汽车,忽略特殊车辆的影响;(3)所有汽车均按指示停靠车辆,在停车楼内均按照单行道限速匀速行驶;(4)车道均符合所有车辆的最小平曲线半径标准,忽略车辆出车时间;(5)停车楼已经具备详细的历史泊车信息,并且进入停车楼的车辆要选择预计离开时间段.
1.2 数学模型
在停车位数量有限、通道内车辆保持安全车距,以及不超过停车场最大容量的约束下,建立以既定周期内所有驶离停车场车辆的总驶离用时最少为目标的优化模型.停车楼每一层楼都作为二维背包来看待,横纵坐标分别为i和j,入口和出口分开,分别和图1中上、下方向的旋转坡道相衔接.

图1 停车楼每层车位分布平面示意图
旋转车道共2条单向车道,1条只上不下,另1条只下不上,车辆上、下楼分别通过不同车道.计算每辆车驶离时间时要考虑下楼时间,每下一层楼的用时为固定值,不考虑坡道内突发阻塞用时.目标函数(1)表示在b阶段内停车楼内车辆驶出花费的总时间
目标函数:
(1)
(2)
(3)
(4)
以上变量均为整数,计算为小数时采用向下圆整.
以上各式中:式(3)限制停车楼内停放车辆数不超过停车位数量;式(4)限制停车场内停靠车辆和行驶中车辆的总数不超过停车楼的最大安全容量.T为所有驶出停车场车辆的总用时;将待优化周期内时间以2h为单位分成若干时段,并依序排列,b为排列序号(b=1,2,…,n);Mb为b时段内停车楼内车辆数量的最大值;f为楼层数;i,j分别为某一楼层停车位的横纵坐标;tbfij为b时段f层(i,j)位置的车辆到本层出口的时间;t*为车辆没下一层楼所用时间,单位小时;dfij为f层楼(i,j)位置车辆到本层出口的行驶路程,m;ebfij为0-1变量,当b时段f层(i,j)位置停放车辆时取1,否则取0;v为停车场内匀速行驶速度,km/h;R为停车楼内总停车位数量;L为停车楼长度;W为停车楼宽度;z1为横向安全车距;z2为横向安全车距;k1为横向车道数;k2为纵向车道数;w1为横向车道宽度;w2为纵向车道宽度,以上涉及长度、宽度变量单位均为m.
2 算法设计
本文的停车问题可以看作“二维背包问题”,属于NP难问题.利用动态规划算法为主线思想,每次决策依靠贪婪算法来进行优化.本算法的基础是可获得的详细历史数据平均值作为判断的依据,cb为b时段驶入停车楼的车辆历史平均数;Gb为b时段驶离停车楼的车辆历史平均数;且待驶入车辆取卡时需选择预计离开时段b*(参照b时段的划分).
应用动态规划算法的主要流程如下.
1) 阶段 以时间方式划分阶段,将待优化周期内时间以2 h为单位分成若干阶段.阶段数用b表示.
2) 状态 从b时段开始时停车楼内整体泊车位置为初始状态,b+1时段开始时整体泊车位置为b阶段结束状态.b阶段的可达状态记为Sb,此状态起始时部分位置已经配载完车辆.
3) 决策变量为Xbfij,以贪婪算法为核心的决策集P(Sb)流程图见图2.
4) 动态规划的基本方程
(5)
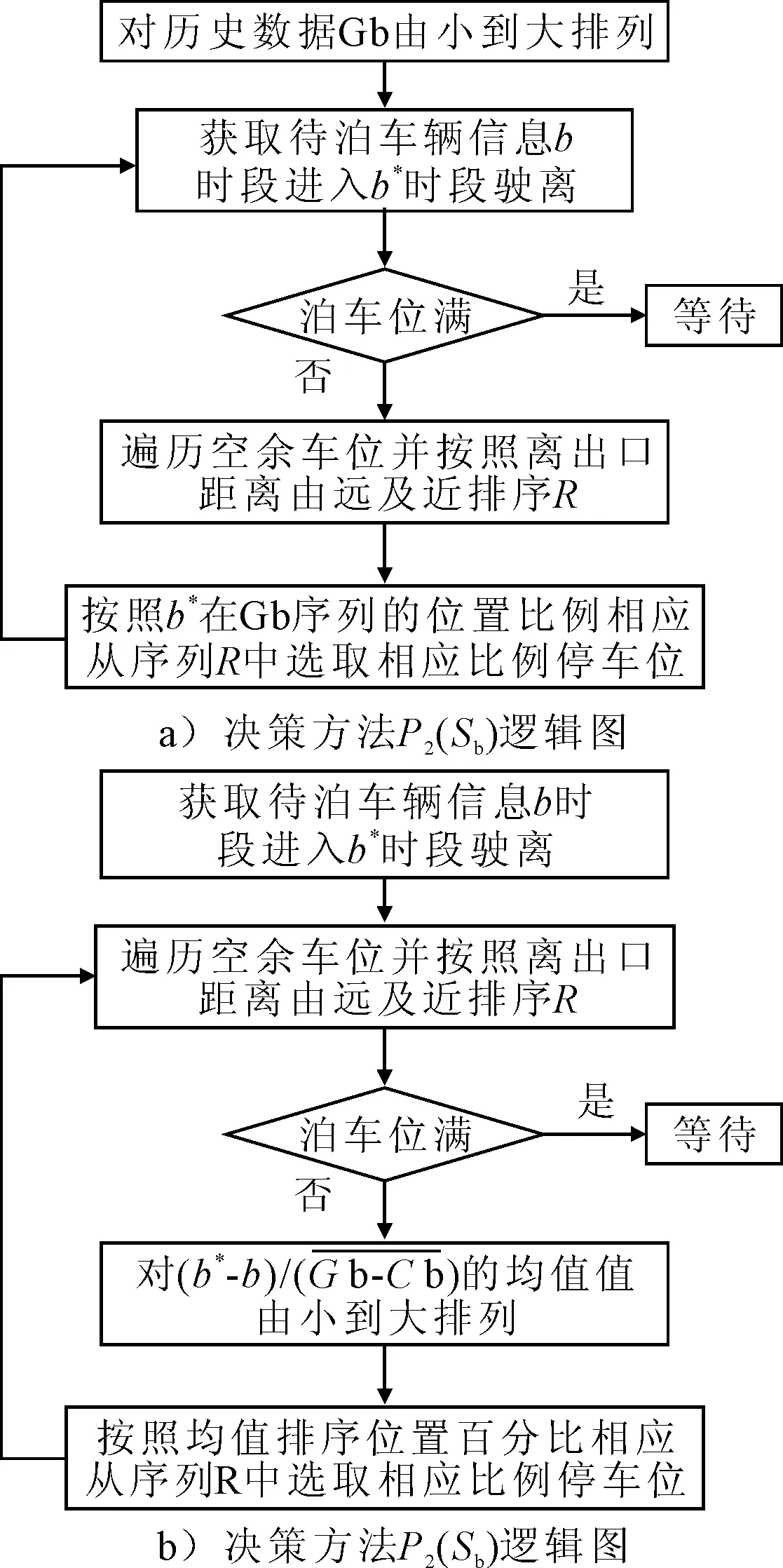
图2 决策方法逻辑图
式中:Xbfij(Sk)=1表示b阶段待停车辆在f层(i,j)位置泊车,否则为0.Ybfij(Sk)=1表示b阶段有车辆在f层(i,j)位置并且驶离,否则为0.
5) 策略 从b阶段开始到终止的所有泊车位置策略的集合.由Pn(Sb)表示,背包问题存在许多备选策略,本文通过贪婪算法确定b阶段每一待停车辆泊车位置的最优策略:Pn(Sb)={x111,x112,…,xfij}.本文选择正序递推法求得最优策略集:Pn(Sb)={P1(S1),P2(S2),…,Pn(Sb)}.实际策略集由实际问题数据计算得出.
3 数值检验
3.1 算例
以现有某停车楼实际数据作为参照,停车楼共有4层,停车位450个,停车楼平面呈1∶2的矩形布置,南北进深50 m,东西跨度100 m,占地面积4 820 m,每层停车位基本平均;建筑层高为3 m,采用旋转式坡道式,车道为3 m的车道.根据历史数据得到历史每天每个时段进入停车场的车辆数的平均值,并按12个时段为周期换算出每个时段进入车辆数占1 d进入车辆数的百分比,见表1.
3.2 结果分析
根据上述混合式启发算法编辑C++程序,其中横向车道数取2,纵向车道数取1,安全车距设定为10 m,平均车速限定为15 km/h,取1 d 12个时段作为计算周期.先对空闲停车楼随机分配即停车辆及其驶离时段信息,然后分别输入共进入200,500及1 000辆车的情况下各个时段分别驶入车辆数的历史平均值,并随机分配给每辆进入车辆驶离时段,见表2.
同时根据相同的初始条件计算采用本文组合优化算法、驶入车辆首选距离出口最近的空位泊车、随机泊车以及驶入车辆首选距离出口最远的空位泊车这4种泊车方式下所有计算时段内驶离停车楼的车辆驶离所耗费总时间,并对结果进行比较分析,见表3.

表1 每天每时段进入停车楼车辆数平均值历史数据

表2 驶离停车场车辆的用时

表3 不同方式驶离车辆总用时比值
根据表3结果可以看出,本方法确实对实际问题达到优化效果,并且对较大数量的停车问题优化效果更为明显,但在更大规模的实验中,由于车位限制,等时过长不具有实际意义,本算法在此算例中的1 000辆车进入规模试验比其他规则减少耗时最为显著,在12.1%~23.6%之间.但更大规模的实验由于车位限制,等时过长不具有优化的实际意义.
4 结 束 语
本文依据历史数据对停车问题通过混合式启发算法进行优化,但是对新型停车设施或者突发性变化适用性不强,需要进一步以自动停车设施及路径跟踪为基础,对已停车辆进行合理自动换位来提高资源利用率,并展开停车楼突发性事件特性研究,提高模型算法的适用性.
[1]张秀媛,董苏华,蔡华民,等.城市停车规划与管理[M].北京:中国建筑工业出版社,2006.
[2]王春洪,查秀萍.停车库投资的可行性分析[J].中外房地产导报,2003(17):40-41.
[3]刘科为,曹麻茹.机械式与坡道式立体停车库横向比较研究[J].南方建筑,2006(3):20-21.
[4]ZIPS P, BÖCK M, KUGI A. A fast motion planning algorithm for car parking based on static optimization[C]∥2013 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS) November 3-7, 2013. Tokyo, Japan.
[5]MING F H, OZGUNER U, A parking algorithm for an autonomous vehicle in proc[J]. IEEE Intelligent Vehicles Symposium. Eindhoven, The Netherlands, 2008(4/6):1155-1160.
[6]KONDAK K, HOMMEL G. Computation of time optimal movements for autonomous parking of non-holonomic mobile platforms[C]∥ Int. Conf. on Robotics & Automation, Seoul, Korea, 2001(3):2698-2703.
Optimization on the Intelligent Parking for a Parking Building Based on Dynamic Programming and Greedy Algorithms
ZHAO Wei1,2)XU Liangjie1)YAO Yihu1)WANG Guanyun1)LI Ge2)
(SchoolofTransportation,WuhanUniversityofTechnology,Wuhan430063,China)1)(CollegeofEconomicsandBusiness,InnerMongoliaUniversityofScience&Technology,Baotou014010,China)2)
Aiming at all types chaos of the multilayer parking management system , time-consuming process and obstruction caused by disorderly parking, according to parking building layout, parking historical database and the information to be parked vehicles, a two-dimensional backpack model is established. A heuristic combined algorithm is proposed by integrating dynamic programming and the greedy algorithm, aiming at making every coming vehicle park in order , optimizing the allocation of resources, reducing parking time and channel blockage and improving parking building utilization.
parking building; greedy algorithm; dynamic programming algorithm; dimensional knapsack problem
2014-11-25
*国家青年科学基金项目资助(批准号:51108361,51208400)
U491.4
10.3963/j.issn.2095-3844.2015.03.012
赵 玮(1988- ):男,博士,讲师,主要研究领域为交通运输规划与管理.
