基于Lyapunov函数的小天体软着陆障碍规避控制方法

胡海静，朱圣英，崔平远

(1.北京理工大学 深空探测技术研究所，北京 100081； 2.飞行器动力学与控制教育部重点实验室，北京 100081)

基于Lyapunov函数的小天体软着陆障碍规避控制方法

胡海静1，2，朱圣英1，2，崔平远1，2

(1.北京理工大学 深空探测技术研究所，北京 100081； 2.飞行器动力学与控制教育部重点实验室，北京 100081)

针对姿轨耦合型探测器控制方法存在工程实现难、计算效率低的问题，提出一种基于Lyapunov函数的小天体自主软着陆障碍规避控制方法。首先，建立了小天体着陆过程姿态和轨道的动力学模型；其次，考虑探测器当前的势能与障碍地形对探测器的威胁选取Lyapunov函数，并根据Lyapunov稳定性原理推导了推力器的开关控制逻辑，能够实现到达目标着陆点的同时进行障碍规避，且该过程不需事先设计参考模型。同时，该控制逻辑具有解析形式，能够实现实时障碍规避。仿真结果表明，该方法能够有效实现规避障碍且满足姿态稳定的要求。

小天体；Lyapunov；障碍规避；姿轨耦合；跟踪控制

0 引 言

随着行星际探测任务的日益增多，探测器在天体表面的安全软着陆已经成为未来深空科学探测的重要任务和课题。为了对有科学价值的区域进行研究和取样，希望探测器能够在危险(岩石、弹坑和陡坡)的区域进行安全着陆。

探测器自主障碍规避是在获取着陆区地形信息前提下，规划满足探测器机动性能的运动轨迹，通过姿、轨控制系统完成推力器开关控制，达到跟踪运动轨迹与稳定姿态的目的。对此，JPL实验室与约翰逊空间中心联合开发了一套基于激光扫描雷达的障碍规避控制算法，用于实现火星表面着陆的障碍规避[1]。另外，为了实现障碍规避过程中探测器6个自由度控制，JPL实验室也做了大量研究[2]。以上过程均利用探测器当前状态和着陆点信息设计多项式轨迹，该方式计算简单，然而，无法避免探测器规避过程中与障碍发生碰撞。采用势函数的制导方法有望解决上述问题，根据探测器当前的势能与障碍地形对探测器的威胁选取Lyapunov函数，并通过Lyapunov稳定性原理推导稳定制导律，因而能够保证探测器到达目标点的同时有效降低碰撞的概率[3]。在实际工程中，障碍规避技术也在我国的“嫦娥3号”探月任务中得到应用，实现避障精度优于5 m[4]。

大行星着陆器往往采用反推发动机和姿态推力喷嘴的构型，而小天体引力较弱，无需采用反推发动机进行减速。在小天体实际任务中采用喷嘴进行姿态和轨道控制能够满足着陆器减速和平稳到达目标点的要求，“隼鸟号”任务中，由于探测器的姿态控制喷嘴出现部分故障，最终同时依靠电推力和喷嘴完成了附着过程的姿态和轨道控制。采用喷嘴实现附着过程的轨道控制和姿态稳定要求探测器具备姿、轨耦合控制能力。然而，目前，姿、轨耦合探测器软着陆障碍规避控制方法积分等效方法存在执行效率低等问题，难以满足实时性要求。另外，文献[5]提出一种姿轨耦合推力器的开关选择方法，能够完成航天器交会对接过程的姿轨控制，然而该方法依赖事先设计的参考模型。

针对上述问题，本文提出一种基于Lyapunov的小天体自主软着陆障碍规避控制方法。首先，建立了小天体着陆过程姿态和轨道的动力学模型；另外，考虑探测器当前的势能与障碍地形对探测器的威胁选取Lyapunov函数，并根据Lyapunov稳定性原理推导了推力器的开关控制逻辑，能够实现到达目标着陆点的同时进行障碍规避，且该过程不需事先设计参考模型。同时，该控制逻辑具有解析形式，能够满足障碍规避过程实时性要求。

1 动力学模型

1.1 坐标系定义

小天体着陆的姿态和轨道参考坐标系如图1所示[6]。

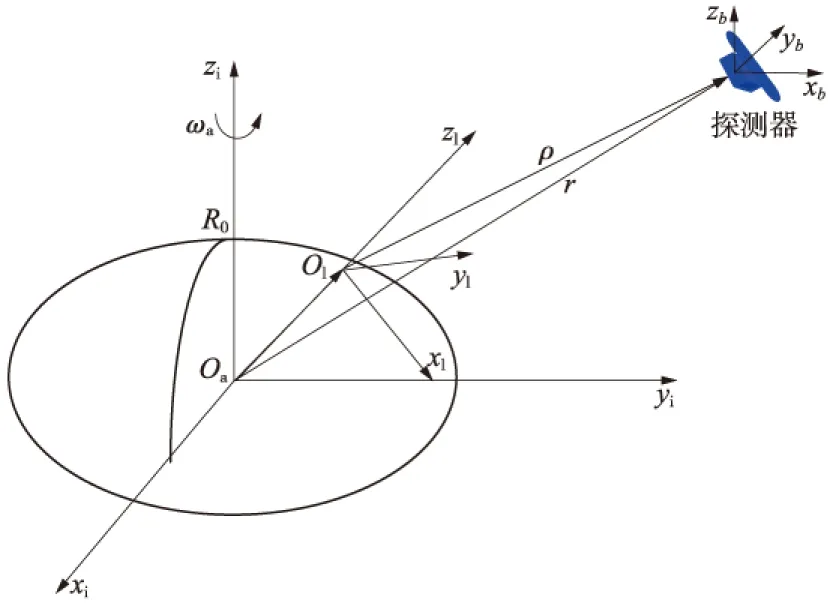
图1 参考坐标系定义Fig.1 Definition of reference system

着陆器本体坐标系为∑b:ob-xbybzb，该坐标系原点ob在探测器的质心处，obxb轴、obyb轴及obzb轴分别与探测器的体轴重合。该坐标系可用来反映着陆过程中探测器的空间姿态。

着陆点固连坐标系为∑l:ol-xlylzl，该坐标系原点ol位于预定的着陆点，olxl沿经线的切线指向南极方向，olzl和从小行星质心指向着陆点的矢量oaol方向一致，olyl与olxl、olzl之间满足右手系法则。着陆器本体坐标系到着陆点固连坐标系的转换矩阵记作LRB。

1.2 姿轨动力学

采用修正罗德里格参数(MRPs)作为姿态表达式，便于将姿态动力学方程写为一般形式的二阶非线性微分方程。着陆器姿态采用MRPs描述，其中，姿态角σ∈R3，角速度ω∈R3，则MRPs参数描述的运动学方程为

(1)

其中

(2)

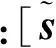
(3)

刚体的姿态动力学方程为

(4)

其中：J=diag(J1J2J3)转动惯量的对角矩阵；M是着陆器本体坐标系中的控制力矩向量。

通过转化，可以将姿态动力学写成二阶非线性微分方程的形式

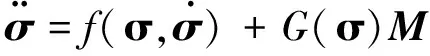
(5)

考虑小天体障碍规避过程距离小天体表面很近，目标天体的自旋角速度对探测器的影响较小，着陆点坐标系下着陆器的动力学方程可以近似表示为如下形式

(6)

其中：SFb为探测器本体坐标系下三轴的控制加速度；LRS为本体系到着陆点坐标系的转换矩阵；gp为目标天体产生的引力加速度。

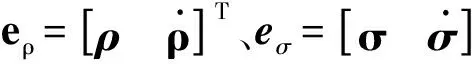
(7)

(8)

令e=[eρeσ]T，则姿轨动力学方程可以表示为

(9)

其中

1.3 探测器构型

为了实现小天体障碍规避过程的平动和转动运动，探测器需要能够同时生成控制力和控制力矩。图2为一种工程中常见的推力器分布构型，在本体坐标系下，其控制力和力矩可以表示为

(10)

其中：ua推力的大小；H为推力器分布构型决定的控制力和力矩的分配矩阵；u=[u1u2… u12]T为推力器的开关状态

(11)

令dx、dy和dz表示推力器的力矩，则分配矩阵HF和HM可表示为

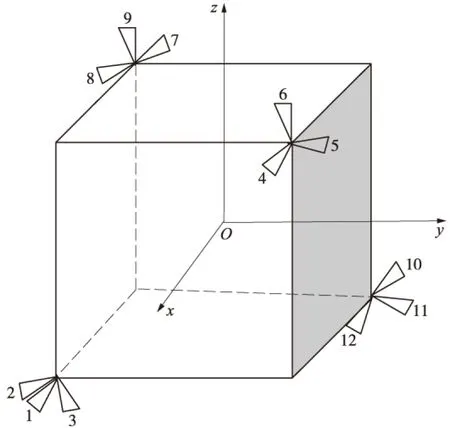
图2 推力器分布结构Fig.2 Thrusters’ configuration of the lander

2 基于Lyapunov函数的障碍规避姿轨控制方法

障碍规避控制系统利用获取的着陆区地形信息，结合导航系统给出的着陆器的位置、速度等信息，产生的控制信号驱动发动机来完成着陆器自主障碍规避。由于未来的科学考察需要，使得着陆区地形复杂，分布着各种障碍，因此在着陆器进行障碍规避时要注意避免与这些障碍发生碰撞。同时，由于星载机运算能力有限，要求障碍规避控制算法简单、可靠，这使得障碍规避控制算法要具有解析表达式。本节给出一种基于Lyapunov函数的障碍规避控制方法，选取的正定Lyapunov函数由状态函数与危险地形势函数两部分组成，通过采用Lyapunov稳定性原理推导了其推力器开关控制方法，能够保证实现障碍规避的同时稳定姿态。

选取正定状态函数为

(12)

选取危险地形势函数为

(13)

其中：xi、yi代表了障碍的位置；zi代表了障碍的高度或深度；k1、σ1是正数；i是障碍的编码。该函数代表了当前所处位置障碍对着陆器的威胁，该函数越大代表当前所处地势越危险，反之越安全。

选取Lyapunov函数

(14)

ΦP和ΦS均为正定，因此

Φ>0

(15)

其中：Δ=Δρ+Δσ+δs

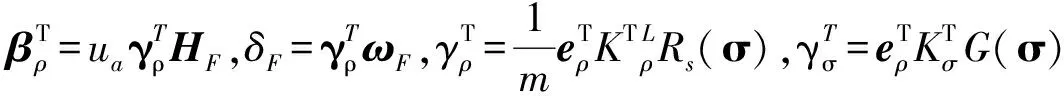
从而，可以得出

(16)

如果Δ<0，则系统将在状态空间平衡点处是一致渐进稳定的。

对于任意一个正定矩阵Q，矩阵P是Lyapunov方程的特解

(17)

根据Lyapunov原理，如果2eTPB(σ)(Hu-ω)≤0，则误差方程渐近稳定。

则可求得

其中

则式(15)可以写成如下形式

(18)

(19)

(20)

然后，βρ和βσ能够写成φ和π的函数

(21)

向量βρ和βσ中的元素如表1所示。

表1 向量βρ和βσ中的元素

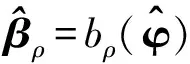
4)计算

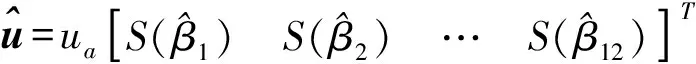
3 仿真结果与分析

为了验证上述算法和公式推导的可行性和可靠性，本文针对小天体障碍规避为例进行了数学仿真。在障碍规避算法中，采用的状态函数的加权系数取值p1、p2、p3取0.002，p4、p5、p6取0.02，地势加权k1为0.2，形状系数σ1取值2，函数下降系数kx=ky=kz=0.2。从初始位置处进行障碍规避，这些障碍信息如表2中所示，选取的目标着陆点为rf=[0，0，0]m，初始位置为[35，80，50]m，初始速度为[0.5，-0.5，-0.8]m/s，小天体引力[0，0，0.001]m/s2，推力大小ua=15N，m=200kg。

表2 障碍信息

图3 三轴位置Fig.3 Position of the lander

图4 三轴速度Fig.4 Velocity of the lander

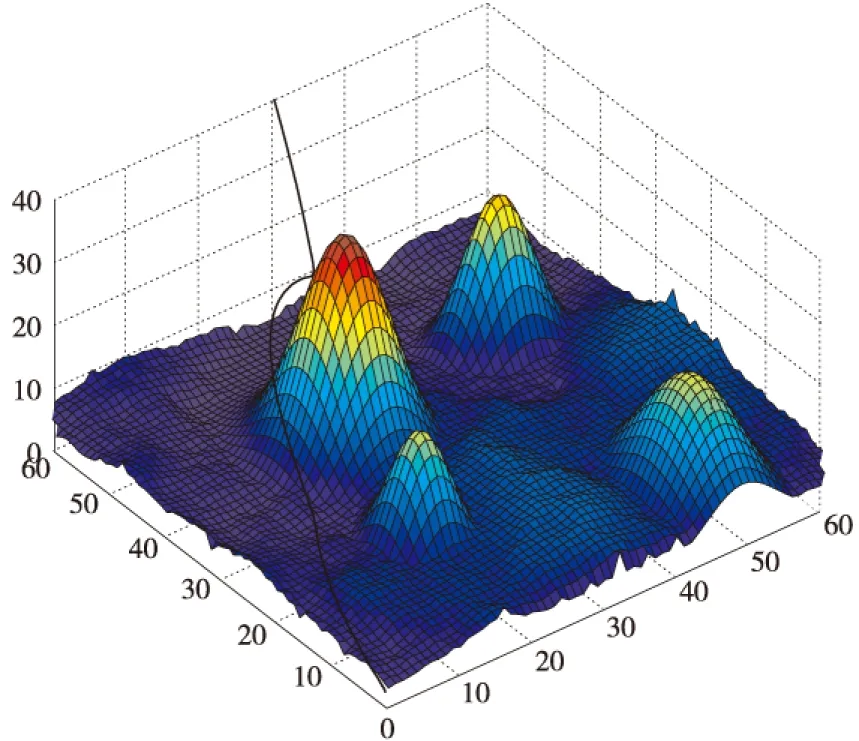
图5 障碍规避轨迹Fig.5 Hazard avoidance trajectory

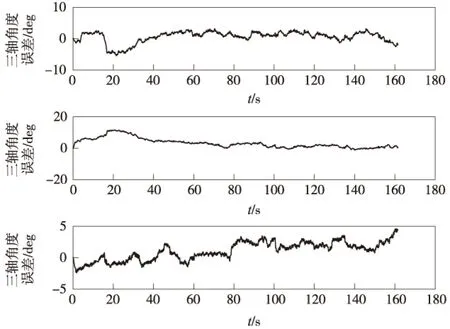
图6 姿态稳定误差Fig.6 Attitude errors

图3为着陆器的三维位置曲线，从中可以看出着陆器的位置逐渐逼近目标点。图4为着陆器障碍规避过程的速度曲线，能够达到在小天体表面软着陆的速度要求。另外，着陆区障碍对着陆器位置和速度曲线的曲率有较大影响，在障碍地形区的着陆轨迹如图5所示，从中可以看出，着陆器能够实现规避障碍的目标。由于障碍规避过程没有涉及姿态机动，在整个过程中姿态稳定误差如图6所示，可以看出在整个障碍规避过程中着陆器姿态保持平稳。以上仿真表明，本文提出的姿轨耦合控制方法能够完成障碍规避的同时实现着陆器姿态稳定，使探测器安全、平稳下降到目标着陆点。另外，由于该推力器开关控制过程具有解析的表达式，因而具有计算效率高的优点。

4 结 论

针对姿轨耦合型探测器控制方法存在工程实现难、计算效率低的问题，本文提出了一种基于Lyapunov函数的小天体自主软着陆障碍规避控制方法。该方法考虑探测器当前的势能与障碍地形对探测器的威胁选取势函数，并根据Lyapunov稳定性原理推导了推力器的开关控制逻辑，能够实现到达目标着陆点的同时进行障碍规避，而且，该过程不依赖参考模型，能够实现自主运行。同时，该控制逻辑具有解析形式，能够满足障碍规避过程实时性要求。

[1] Johnson A E， Klumpp A R， Collier J B， et al. Lidar-based hazard avoidance for safe landing on Mars[J]. Journal of Guidance， Control， and Dynamics， 2002，25(6):1091-1099.

[2] Wong E C， Singh G. Guidance and control design for hazard avoidance and safe landing on Mars[J]. Journal of Spacecraft and Rockets， 2006，43(2):378-384．

[3] Zhu S Y， Cui P Y， Hu H J. Hazard detection and avoidance for planetary landing based on Lyapunov control method[C]∥Intelligent Control and Automation. Beijing: [s.n.], 2012.

[4] 张洪华，梁俊，黄翔宇，等.嫦娥三号自主避障软着陆控制技术[J].中国科学:技术科学，2014，44(6):559-568. [Zhang H H， Liang J， Huang X Y， et al. Autonomous hazard avoidance control for Chang’E-3 soft landing[J]. Sci. China， 2014，44(6):559-568.]

[5] Curti F， Romano M， Bevilacqua R. Lyapunov-based thrusters’ selection for spacecraft control: analysis and experimentation[J]. Journal of Guidance Control and Dynamics， 2010，33(4):1143-1160．

[6] 朱圣英，崔平远，崔祜涛，等.基于路标观测角的星际着陆器自主位姿确定技术[J].航空学报，2010，31(2):318-326. [Zhu S Y， Cui P Y， Cui H T， et al. Autonomous position and attitude determination for interplanetary landers based on landmark observation angles[J]. Acta Aeronautica Et Astronautica Sinica， 2010，31(2):318-326.]

[责任编辑：宋宏]

Lyapunov-Based Hazard Avoidance Control Method for Landing on Small Celestial Bodies

HU Haijing1，2， ZHU Shengying1，2， CUI Pingyuan1，2

(1. School of Aerospace Engineering， Beijing Institute of Technology， Beijing 100081， China； 2. Key Laboratory of Dynamics and Control of Flight Vehicle， Ministry of Education， Beijing 100081， China)

Aiming at the difficulty in designing the coupled attitude and orbit control lander， the lyapunov-based hazard avoidance control method for landing on small celestial bodies is presented. Firstly， the dynamic model is given， and the is selected based on the current potential of the lander and the threat from the hazards. Then， the on-off logic of the thrusters is derived according to the Lyapunov theory. This guarantees that the lander can arrive at the landing site and avoid the hazards， and this process . Since the control logic is analytical， this control method can meet the real-time requirement of hazard avoidance and is easy to be applied in the engineering. The simulation results show that this method can avoid the hazards effectively and stabilize the attitude.

small celestial bodies； Lyapunov； hazard avoidance； coupled attitude and orbit system； tracking control

2014-10-14

2014-12-30

国家重点基础研究发展计划(973计划)资助(2012CB720000)；国家自然科学基金资助(60874094)；高等学校博士学科点专项科研基金资助(20111101110001)；北京理工大学创新团队

V447.2

A

2095-7777(2015)02-0149-06

10.15982/j.issn.2095-7777.2015.02.008

胡海静(1986—)，男，博士生，主要研究方向：行星着陆导航制导与控制。 通信地址：北京理工大学宇航学院22信箱(100081) 电话：(010)68918921 E-mail:bithuhaijing@163.com