飞往日-地动平衡点轨道初始误差敏感度分析

王亚敏，乔栋，崔平远

(北京理工大学 宇航学院， 北京 100081 )

飞往日-地动平衡点轨道初始误差敏感度分析

王亚敏，乔栋，崔平远

(北京理工大学 宇航学院， 北京 100081 )

对从环月轨道飞往日-地动平衡点轨道的转移轨道初始误差敏感度进行了数值仿真与分析。介绍了两种类型的转移轨道：长转移与短转移。建立初始速度误差与轨道末端偏差之间的数学关系式，采用数值计算获得了初始速度误差与轨道末端偏差量之间的线性关系曲线。通过建立轨道初始状态与末端状态量的一阶变分表达式，来说明始末偏差量呈线性关系的原因以及适用范围。研究表明，长转移轨道相较于短转移，对初始速度误差更为敏感，其始末偏差的线性关系适用范围更小。

日-地动平衡点；日-地-月系统；敏感度分析

0 引 言

动平衡点又称拉格朗日点或平动点，是三体系统中的引力平衡点。日-地三体系统共线动平衡点，由于其特殊的空间位置——始终位于日-地连线，是太阳探测、空间环境探测以及空间观测的理想场所。同时，平衡点在低能量转移轨道设计中也起着关键作用[1]。研究表明，月球平衡点和日-地系统共线动平衡点之间存在零消耗或者低消耗转移，这类转移是人类以低能量方式进入近地空间或者探测太阳系大行星、小行星的主要途径[2-4]。

周期轨道、拟周期轨道以及三体系统中的不变流形结构构成了设计低能量转移轨道的主要要素。近十多年来，世界各国的航天器轨道设计者和动力系统理论研究人员对如何应用该低能量要素来设计低能量轨道进行了广泛的研究：例如地-月/日-地系统动平衡点任务轨道设计[5-6]、火星halo轨道的低能量捕获问题[7-8]、三体系统共线动平衡点之间的转移轨道设计问题[9-11]等。然而，当探测器从地-月系统向日-地系统转移时，地球、太阳、月球引力同时作用于探测器，并且任一天体的引力影响都不可忽略，这将为轨道设计带来新的困难：转移轨道设计需要考虑日-地-月系统与探测器构成的四体动力学模型。Koon等(2000，2001)通过将四体动力学模型拆分成两个重合的三体系统：日-地三体系统和地-月三体系统，成功地采用动平衡点轨道及其不变流形来设计两个三体系统之间的转移[12-14]。

针对日-地-月四体动力学模型下的转移轨道设计问题，Koon、Howell、Gómez、Masdemont等对其进行了广泛的研究，包括平面模型、三维模型、halo-halo转移、拟周期轨道之间的转移等[4，12-16]。作为我国探月工程2期的“嫦娥2号”探测器，在世界上首次成功地实现了地-月系统到日-地系统之间的低能量转移[17-19]。针对复杂的工程任务约束条件，Qiao等(2013)在真实星历模型对“嫦娥2号”探测器的转移轨道设计问题进行了研究，通过搜索地-月系统中探测器从环月轨道逃逸的弹道轨道与日-地系统Lissajous轨道的稳定流行在空间Poincare界面的交点来构建低能量的转移[18]。Masaki等(2014)在较为简单的动力学模型——日-地圆形限制性三体模型下对日-地L2点周期轨道的稳定流行与月球轨道相交的情况进行了分析，大致刻画了转移机会存在的区域及其特征[20]。

多体系统的强非线性动力学环境在带来低能量特性的同时，也给轨道控制提出了难题。探测器从月球出发向日-地空间转移时，由于靠近地球和月球(并未远离地球影响球)，同时受到月球、地球、太阳引力的作用，对轨道机动误差极为敏感。本文将对该类转移轨道在逃逸脉冲存在扰动情况下，实际飞行轨迹与标称轨迹偏差进行计算与分析，以加深日-地-月四体动力学模型下，转移轨道对初始扰动敏感度的理解。在之前的研究中，Masaki等(2014)[20]发现，从月球飞往日-地L2点周期轨道的转移轨道存在两种类型，它们被称之为长转移和短转移。这两类轨道各有特点：长转移耗时长，但逃逸脉冲较小；短转移耗时短，但逃逸脉冲较大。本文将对这两类轨道的初始误差敏感度进行分析，为轨道设计工作者对此类型轨道提供一个更全面的认识。

1 动力学模型

1.1 日-地-月动力学模型

本文的研究对象是日-地-月四体动力学模型下的轨道，因此运动方程需要考虑月球、地球和太阳的引力作用。在本文的研究工作中，参考坐标系为月心J2000，探测器的动力学方程为

(1)

其中：μm，μe，μs分别为月球、地球和太阳的引力常数，本文的取值分别为：1.327 12e-11，3.986 004 36e-5，以及4.902 800 07e-3 km3/s2。动力学方程中的位置矢量定义如图1所示，它们的瞬时位置通过JPL实验室的DE405计算获得。本文的积分程序为Runge-Kutta 7/8阶积分器，积分误差为1e-13。

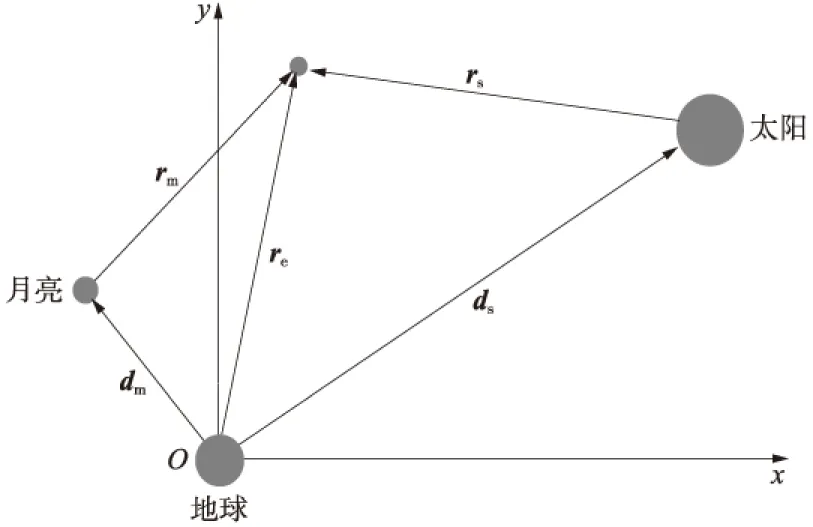
图1 有太阳引力摄动的地心轨道动力学模型Fig.1 Earth-center model with gravities perturbation of Sun and Moon

1.2 动平衡点轨道

众所周知，在圆形限制性三体动力学系统中存在5个拉格朗日点，其中3个为共线动平衡点(位于两个主天体连线上)，L1～L3，另外两个为三角动平衡点L4～L5，分别与L1和L2构成等边三角形。在太阳系中，太阳-大行星所构成的三体系统，其共线动平衡点均为不稳定，三角动平衡点均为稳定。研究表明，在共线动平衡点附近存在这周期轨道和拟周期轨道簇，Lissajous、Halo以及Lyapunov轨道。对于任一Jocabi常数，在动平衡点周围存在一个垂直Lyapunov轨道、一个水平Lyapunov轨道、南向和北向共两条Halo轨道、Lissajous轨道簇和quasi-halo轨道簇。

2 转移轨道及其对初始误差敏感度分析方法

2.1 两种转移轨道

先前的研究表明，从月球环月轨道到日-地动平衡点存在两种类型的转移。若根据逃逸脉冲大小、飞行时间长短以及转移机会聚集区域对转移轨道进行了分类，则存在高脉冲、短飞行时间转移轨道和低脉冲、长飞行时间转移轨道两种轨道簇，我们称之为短转移和长转移。以飞往日-地L2点为例，对于前者，探测器从地-月与地-日矢量夹角约90°方位逃逸，之后直接飞往动平衡点区域；对于后者，探测器离开环月轨道之后，将靠近月球轨道继续飞行一段时间。本文以向日-地L2点转移为例，在两种类型转移轨道中各挑选一条，对其中途修正机动特性进行了分析。转移轨道飞行轨迹如图2～图3所示，其轨道初始参数如表1所示。

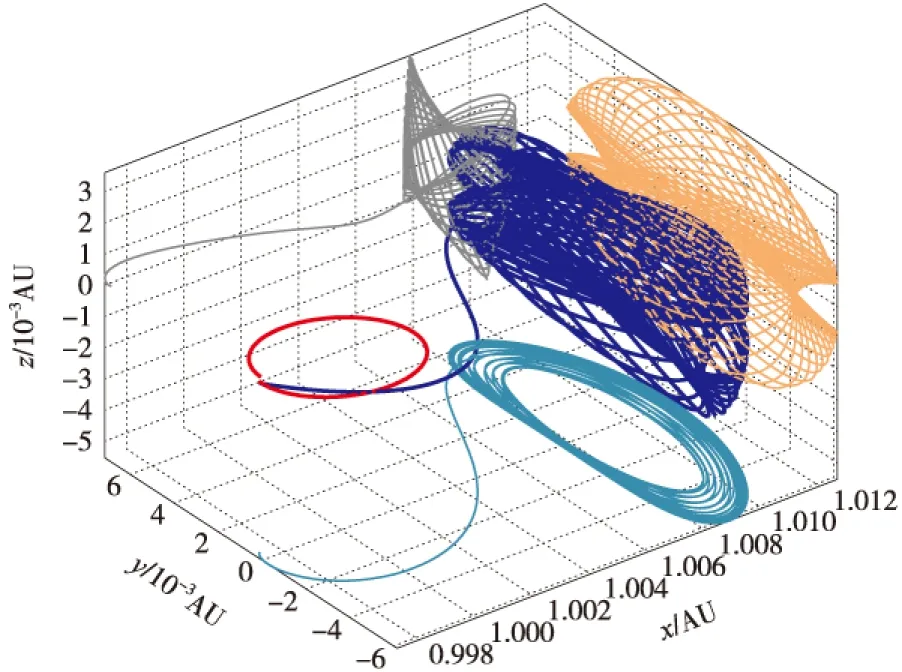
图2 低脉冲、长时间转移轨道(长转移)Fig.2 Small-impulse and long-time transfer

图3 高脉冲、短时间转移轨道(短转移)Fig.3 High-impulse and short-time transfer

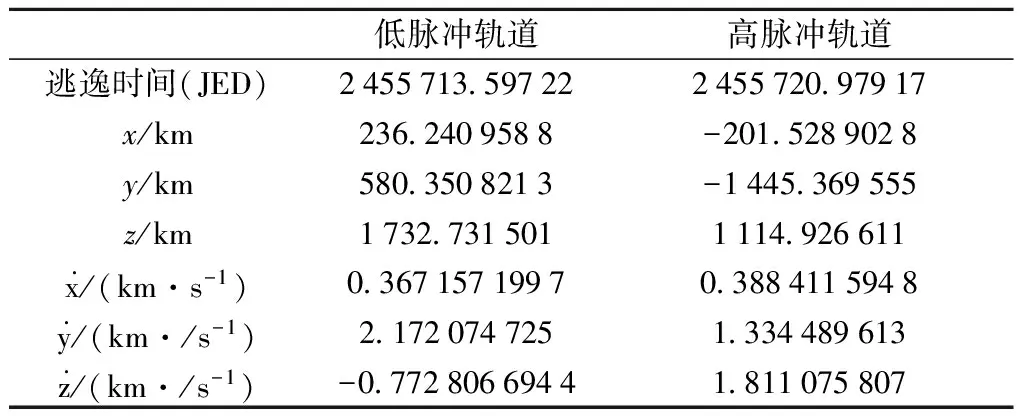
低脉冲轨道高脉冲轨道逃逸时间(JED)245571359722245572097917x/km2362409588-2015289028y/km5803508213-1445369555z/km17327315011114926611x/(km·s-1)0367157199703884115948y/(km·/s-1)21720747251334489613z/(km·/s-1)-077280669441811075807

2.2 初始误差及敏感度分析方法

2.2.1 初始误差

假设探测器在逃逸时刻，执行逃逸脉冲存在误差。本文考虑的误差仅仅改变初始速度大小而不改变方向。我们可以将实际的转移轨道初始速度写为

(2)

2.2.2 敏感度分析

对于转移轨道中途修正而言，由于随着时间递推，轨道机动误差被逐渐放大，对于三体系统低能量转移轨道而言，这种误差放大效果更为明显。因此，应该尽早安排第一次轨道中途修正。通过分析各国深空探测任务，考虑到在逃逸机动之后，轨道精确测量需要一定的时间，第一次轨道中途修正一般被安排在探测器逃逸机动2天之后。本文的主要工作就是分析受到扰动后的航天器在经过2～11天的飞行后，与标称轨道之间的距离。探测器的运动方程可以写为

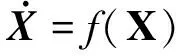
(3)

其中：X为探测器的状态变量。设φ(t，X1)为探测器在初始状态为t1=0，X=X1时的解，那么受到初始速度扰动后的转移轨道与标称轨道之间的偏差可以写为

(4)

以上建立了通过数值积分直接求解轨道末端偏差的数学模型。如若我们将式(4)写成如下形式

(5)

并在X1处泰勒展开，保留一阶，结果为

(6)

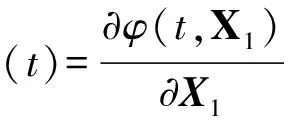
(7)

本文采用式(4)对转移轨道初始误差所导致的末端偏差进行计算，同时借助状态转移矩阵(6)式对结果进行了系统的分析。

3 仿真分析

3.1 两类转移轨道在相同初始速度扰动条件下的响应

对两类转移轨道的初始速度施加相同的速度扰动ε，ε∈[-1，1] m/s，仿真步长为0.2 m/s。轨道递推时间t∈[2，11]天，仿真步长为1天。通过数值计算，速度扰动ε以及时刻t对ΔR的影响，如图4～图5所示。其中图4对应短转移轨道，图5对应长转移轨道。图中x轴为初始速度扰动(m/s)，y轴为末端偏差ΔR(km)，图中每一条曲线代表一个t值。

图4 短转移轨道对初始误差的敏感度分析Fig.4 Sensitivity of short transfer to initial error

图5 长转移轨道对初始误差敏感度分析Fig.5 Sensitivity of long transfer to initial error

从图4与图5可见，短转移和长转移具有以下特性：从末端偏差大小来看，相同的初始速度误差和轨道递推时间，短转移的末端偏差值(不大于5 000 km)要远远小于长转移(最大值约3万km)；从末端偏差与初始误差关系来看，二者为线性关系，末端偏差量正比于初始速度误差；从末端偏差量与飞行时间关系来看，当初始误差一定时，飞行时间越长，末端偏差量越大。因此，对于探测器的实际飞行任务而言，轨道中途修正越早实施越好；相比于短转移，长转移对初始速度误差更为敏感。

3.2 对线性关系的解释

由第3.1节的分析可见，长转移与短转移的末端偏差量与初始速度误差为线性关系，本节将对这一现象进行解释与分析。式(6)给出了初始状态与末端状态之间的一阶差分关系，即ΔXt=φ(t)ΔX1。当飞行时间t一定时，状态转移矩阵φ(t)为一常矩阵，显然ΔXt与ΔX1为线性关系。这就是我们从图4与图5所看到的线性曲线。但是，状态转移矩阵φ(t)表示转移轨道末端状态Xt对初始状态X1的导数关系，即∂Xt/∂X1。式(6)是函数φ(t，X1)在X1附近的一阶展开。由于省略了二阶以上的高阶项，则式(6)的准确性取决于ΔX1取值大小、φ(t，X1)对X1的非线性强度。

在第3.1节中，速度误差最大值为1m/s。这里速度误差取值最大为6m/s。从图6(a)可见，对于长转移而言，当飞行时间t≤6天时，ΔX1与ΔX1之间的线性关系依然保持，即初始误差取值6m/s，一阶泰勒展式依然较为精确；当飞行时间大于6天时，线性关系被破坏，这是由于随着飞行时间的延长，飞行轨道相对于初始状态的非线性程度在增加。从图6(b)可见，对于短转移而言，当飞行时间为80天以内时，6m/s的速度误差依然能采用一阶近似来计算末端偏差量；当飞行时间达到120天时，一阶线性近似已经不能满足始末偏差之间的近似。可见随着飞行时间的增长，泰勒展式(6)的高阶项不能被忽略。相比于长转移，短转移轨道始末偏差量一阶泰勒展开的适用范围更广。另外，我们针对短转移轨道，计算了范围更大的初始速度偏差(最大值50m/s，飞行时间为10天)时的末端偏差量，希望获得在满足始末端状态偏差量的近似线性关系前提下，ΔX1的取值范围，其结果如图7所示。从图中可见，30m/s以内的速度误差依然能保持与末端偏差量的近似线性关系。

图6 速度误差与末端偏差之间的曲线关系Fig.6 Relationship between velocity error and terminal derivation

图7 短转移的50 m/s速度误差与末端偏差之间的曲线关系Fig.7 Relationship between velocity error of 50 m/s and terminal derivation for short transfer

4 结 论

本文针对从环月轨道向日-地L2点动平衡点轨道转移的转移轨道初始误差敏感度进行了仿真计算与分析，获得了如下结论：

1)通过转移轨道数值积分，当初始速度误差较小时，约1 m/s，轨道末端偏差量与初始误差呈线性关系；相较于短转移，长转移对初始误差更为敏感。

2)末端偏差量在初始偏差X1附近的一阶泰勒展开式表明，初始速度偏差与末端位置偏差为线性关系，即结论1)；一阶泰勒展开式由于忽略了高阶项，随着初始速度偏差的增大或者飞行时间的增加，一阶近似(线性关系)并不能准确描述始末状态偏差量的关系。

[1] Canalias E， Gomez G， Marcote M， et al. Assessment of mission design including utilization of libration points and weak stability boundaries[EB/OL].[2014-10-14].http://www.esa.int/act．

[2] Farquhar RW， Dunham D W， Guo Y， et al. Utilization of libration points for human exploration in the Sun-Earth-Moon system and beyond[J]. Acta Astronautica， 2004，55(3):687-700．

[3] Canalias E，Masdemont J J. Computing natural transfers between Sun-Earth and Earth-Moon Lissajous libration point orbits[J]. Acta Astronautica， 2008，63(1):238-248．

[4] Howell K C，Kakoi M. Transfers between the Earth-Moon and Sun-Earth systems using manifolds and transit orbits[J]. Acta Astronautica， 2006，59(1):367-380．

[5] Gómez G， Jorba A， Masdemont J J， et al. Study of the transfer from the Earth to a halo orbit around the equilibrium point L1[J]. Celestial Mechanics and Dynamical Astronomy， 1993，56(4):541-562．

[6] Barden B T， Howell K C， Lo M W. Application of dynamical systems theory to trajectory design for a libration point mission[J]. Journal of the Astronautical Sciences， 1997，45(2):161-178．

[7] Nakamiya M， Scheeres D J， Yamakawa H， et al. Analysis of capture trajectories into periodic orbits about libration points[J]. Journal of Guidance， Control， and Dynamics， 2008，31(5):1344-1351．

[8] Wang Y， Qiao D， Cui P. Analysis of two-impulse capture trajectories into Halo orbits of Sun-Mars system[J]. Journal of Guidance， Control， and Dynamics， 2014，37(3):985-990.

[9] Davis K E， Anderson R L， Scheeres D J， et al. The use of invariant manifolds for transfers between unstable periodic orbits of different energies[J]. Celestial Mechanics and Dynamical Astronomy， 2010，107(4):471-485．

[10] Gómez G，Masdemont J J. Some zero cost transfers between libration point orbits[C]//AAS PAPER 00-177， AAS/AIAA Astrodynamics Specialist Conference. [S.l.]:AAS/AIAA，2000．

[11] Howell K C， Hiday-Johnston L A. Time-free transfers between Libration-Point orbits in the elliptic restricted problem[J]. Acta Astronautica， 1994，32(4):245-254.

[12] Koon W S， Lo M W， Marsden J E， et al. Shoot the Moon[C]//AAS/AIAA Space Flight Mechanics Meeting. Clearwater， Florida: AAS/AIAA， 2000．

[13] Koon W S， Lo M W， Marsden J E， et al. Low energy transfer to the Moon[J]. Celestial Mechanics and Dynamical Astronomy， 2001(81):6373．

[14] Gómez G， Koon W S， Lo M W， et al. Connecting orbits and invariant manifolds in the spatial three-body problem[J]. Nonlinearity， 2004，17(5):1571-1606．

[15] Gómez G，Koon W S， Lo M W， et al. Invariant manifolds， the spatial three-body problem and space mission design[D].[S. l.]: AAS， 2001.

[16] Parker J S，Lo M W.Shoot the Moon 3D[C]//AAS/AIAA Astrodynamics Specialists Conference. Lake Tahoe. California: AAS/AIAA, 2005.

[17] Wu W R， Liu Y， Liu L， et al. Pre-LOI trajectory maneuvers of the Chang’e-2 libration point mission[J]. Science China Information Sciences， 2012，55(6):1249-1258．

[18] Qiao D， Cui P Y， Wang Y M， et al. Design and analysis of an extended mission of CE-2: From lunar orbit to Sun-Earth L2 region[J]. Adv Space Res, 2014,54(10):2087-2093.

[19] 吴伟仁，崔平远，乔栋，等.嫦娥二号日地拉格朗日L2点探测轨道设计与实施[J].科学通报，2012，57:1987-1991.[Wu W R， Cui P Y， Qiao D， et al. Design and performance of exploring trajectory to Sun-Earth L2 point for Chang’E-2 mission[J]. Chin Sci Bull (Chin Ver)， 2012，57:1987-1991.]

[20] Masaki N，Kawakatsu Y. Transfer trajectories from the Moon to Sun-Earth halo orbits[J]. Journal of Guidance， Control， and Dynamics， 2014，37(3):1000-1003．

[责任编辑：高莎]

Sensitivity Analysis of Initial Error for the Trajectory to the Sun-Earth Libration Point

WANG Yamin， QIAO Dong， CUI Pingyuan

(School of Aerospace Engineering， Beijing Institute of Technology， Beijing 100081，China)

The sensitivity of initial error for the transfer trajectory from lunar orbit to the Sun-Earth libration point orbit was calculated and analyzed. First， the short and long transfer trajectories for this kind of transfer issue were proposed. Then， the mathematical relation between initial error and terminal derivation was built. The relation is found to be linear by numerical calculation. Finally， the reason why the linear relation existed and its applicable conditions were explored by the first-order variation expression of initial error and terminal derivation. The result indicated that the long transfer is more sensitive to initial error than short transfer and that the applicable conditions for long transfer is stricter.

Sun-Earth libration point; Sun-Earth-Moon system; sensitivity analysis

2014-10-14

2015-04-30

国家基础研究发展计划(973计划)(2012CB720000)；国家自然科学基金(11102020)；新世纪优秀人才支持计划；北京高等学校青年英才计划项目

V412.4

A

2095-7777(2015)02-0125-06

10.15982/j.issn.2095-7777.2015.02.004

王亚敏(1987—)，男，博士，主要研究方向：深空探测轨道动力学与控制。 E-mail：wangyam09@163.com