基于证据理论优化的态势预测模型

汪永伟，刘育楠，赵荣彩，常德显，邱 卫

WANG Yongwei1，2,LIU Yunan1，2,ZHAO Rongcai1,CHANG Dexian1，2,QIU Wei1，2

1.信息工程大学，郑州450004

2.河南省信息安全重点实验室，郑州450004

1.Information Engineering University,Zhengzhou 450004,China

2.Henan Key Laboratory of Information Security,Zhengzhou 450004,China

1 引言

态势预测是网络安全态势感知的必要环节，能够检验安全措施的有效性，并对网络安全状态的发展趋势进行事前预判、“防患于未然”。因此，态势预测已经成为态势感知领域的研究热点之一。

当前，态势预测研究已取得了一定的研究成果。王慧强等人提出了基于遗传算法优化神经网络模型的态势预测方法[1]。李松等人提出了采用粒子群算法对BP神经网络的权值和阈值进行优化，获得最优BP 神经网络模型进行预测的方法[2]。程绪超等人提出了采用多目标优化算法改进Elman 网络的预测方法[3]。李彩虹等人提出了使用神经网络对误差进行校正的组合预测方法[4]。Yan 等人提出了基于相对误差求最优权重组合的预测方法[5]。Xu 等人提出了通过构建相对误差矩阵和线性方程求解最优组合模型的预测方法[6]。Zheng 等人提出了利用信息熵权法构建组合模型权重的方法[7]。

分析现有的研究工作可以看出，现有预测模型研究主要包括两大类：单一预测模型和组合预测模型。由于单一预测模型都是针对曲线的某种特征而设计的，因此，前一种态势预测方法仅能做到对某种特质的态势曲线的高精度预测，在应用上具有一定的局限性；第二种预测模型的思路清晰，预测模型的适应性也更强。现有的组合模型中，组合权重都是依据误差精度进行调整，即依据单指标建立组合模型。然而，在一些情况下，误差精度指标不能全面反映预测子模型的性能优劣程度。如，在平均误差相同的情况下，预测子模型的误差分布可能会有较大差异，依据不均匀误差分布而建立的组合模型在预测性能上会表现出极大的不确定性；此外，态势曲线的变化趋势也是影响预测精度的重要因素。现有组合模型对上述因素尚未给予充分考虑。

针对上述问题，本文提出一种基于证据理论优化的态势组合预测模型（Situation Forecast Model based on Evidence Theory Optimization，SFM_ETO）。SFM_ETO模型首先对参与组合预测的各子模型进行训练，获得各子模型的多指标性能评价；然后利用证据理论对多指标权重进行融合，获得最优的初始权重组合；在组合预测完成后，再次利用证据理论对指标权重进行折扣，强化高可信指标对权重分配的作用，弱化低可信指标对权重分配的影响，从而优化组合模型。

2 基于证据理论优化的态势组合预测算法

2.1 基本思路

网络安全态势随时间并未表现出显著的规律性特征，在某些情况下表现平稳，在另外一些情况下则表现出周期变化或随机变化，因此，只用一种模型很难精确地刻画预测过程[8-9]。本文将能够精确刻画不同特征曲线的典型态势预测模型进行综合，试图利用不同模型各自在态势预测上的优势，取长补短，从而获得更为精确的预测结果。证据理论具有较强的多目标融合决策能力，能够实现综合多源信息，获得更为精确的决策。因此，本文提出一种基于证据理论优化的态势预测模型SFM_ETO。该模型分为四个阶段：训练准备、权重融合、组合预测和优化演进。SFM_ETO 模型的工作过程如图1 所示。

阶段1训练准备

对组合模型的子模型进行训练，获得态势预测子模型的参数、评价指标和权重分配。

阶段2权重融合

基于证据理论对获得的多重评价指标进行权重融合，获得初始的最优组合权重。

阶段3组合预测

利用组合预测算法对态势进行预测。

阶段4优化演进

基于证据理论对组合权重和评价指标进行优化，强化高可信度指标在预测模型评价和权重分配过程中的作用，降低可信度较低的指标对权重决策的不利影响。

2.2 SFM_ETO 模型的子模型

基于2.1 的分析，SFM_ETO 模型将态势分为平稳变化量、周期变化量和随机变化量。本文选择二次指数平滑法、BP 神经网络模型和ARIMA 三种模型用于分别刻画这三种分量。

2.2.1 二次指数平滑法

二次指数平滑法由布朗（Robert G.Brown）提出，是时间序列平滑法的一种[10]。其基本思想是：时间序列的变化态势具有稳定性或规则性，所以时间序列可被合理地顺势推延，可以将其作为下一期预测的基础。二次指数平滑法强调近期数据对预测值的作用，适用于预测变化不大、变动较为平滑的数据。

2.2.2 BP 神经网络预测模型

BP（Back Propagation）网络是神经网络中采用误差反传算法作为其学习算法的前馈网络[11]。其基本思想是：BP 神经网络通常由输入层、输出层和隐含层构成，层与层之间的神经采用全互连的连接方式，通过相应的网络权系数相互联系，每层内的神经元之间没有连接。BP 神经网络模型的自适应性、自学习能力和抗干扰能力强，适用于预测有周期性特征的数据。

2.2.3 ARIMA 预测模型

ARIMA 模型全称为自回归移动平均模型（Autoregressive Integrated Moving Average Model，ARIMA）[12]。其基本思想是：首先对时间序列做平稳性检验；对非平稳时间序列进行差分使其转化为平稳序列，需要的差分次数就是参数d；然后，对ARIMA 的自回归项p和移动平均项q进行识别；最后，建立ARIMA 模型对时间序列进行预测[9]。ARIMA 模型对噪音数据有很强的预测能力，适用于具有非周期性、突变特征的数据预测。

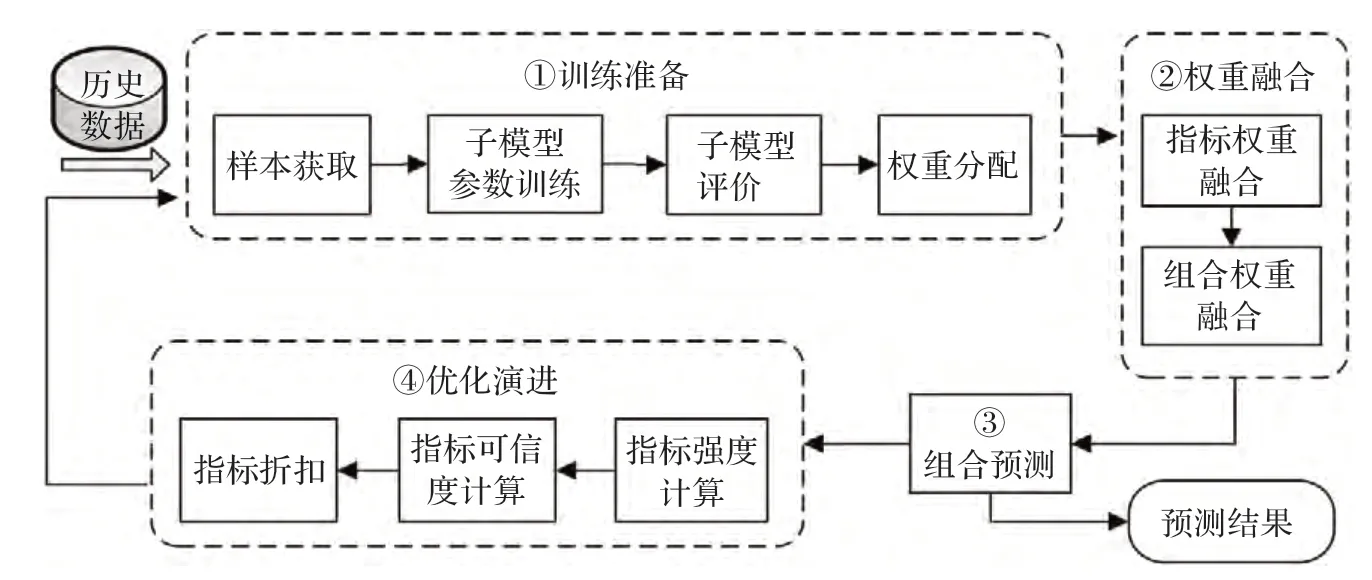
图1 基于证据理论优化的态势预测模型

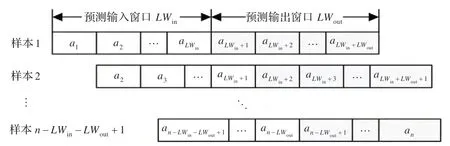
图2 态势预测训练样本集

2.3 训练准备

2.3.1 样本集获取

SFM_ETO 模型采用滑动窗口动态生成样本集。假设已采集的态势样本序列为a1，a2，…，an，预测输入滑动窗口大小为LWin，预测输出滑动窗口为LWout，则第1条训练样本为。预测输入滑动窗口和预测输出滑动窗口依次向右滑动，完成样本集构建。样本集的构建过程如图2 所示。

2.3.2 评价指标与权重分配

2.3.2.1 基于相对误差的权重分配

态势预测一般使用误差来描述预测模型的精度[4]，下面给出相关定义。

定义1绝对误差（Absolute Error，AE）

其中，pi表示预测输出值，ai表示实际输出值。

定义2平均绝对误差（Mean Absolute Error，MAE）

绝对误差的平均值称为平均绝对误差，表示为：

定义3相对误差（Absolute Percent Error，APE）

相对误差可用预测输出值与实际输出值之间的相对差值表示。

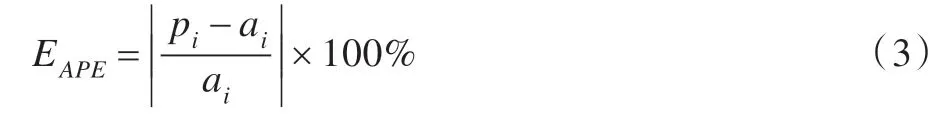
定义4平均相对误差（Mean Absolute Percent Error，MAPE）

相对误差的平均值称为平均相对误差，表示为：

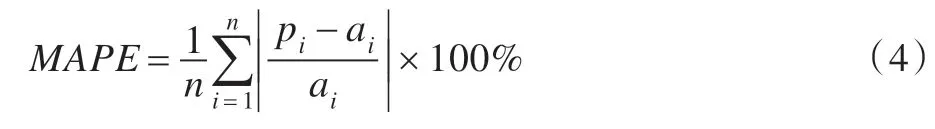
EAPE值越大，表明预测算法的预测精度越低，在组合预测算法中应为其分配越低的权重；反之，应为其分配越高的权重。

通过式（4）计算每个预测算法的相对误差后，对相对误差进行归一化处理，可得每种算法的权重Ew（Error Weight）。

2.3.2.2 基于趋势拟合的权重分配

从数学形式上看，可用连续型时变曲线z=f(t)描述态势的演化过程。对态势数据按照时间间隔τ进行离散采样，得到由采样点(tk，zk)所形成的离散型时间序列。如图3 所示。

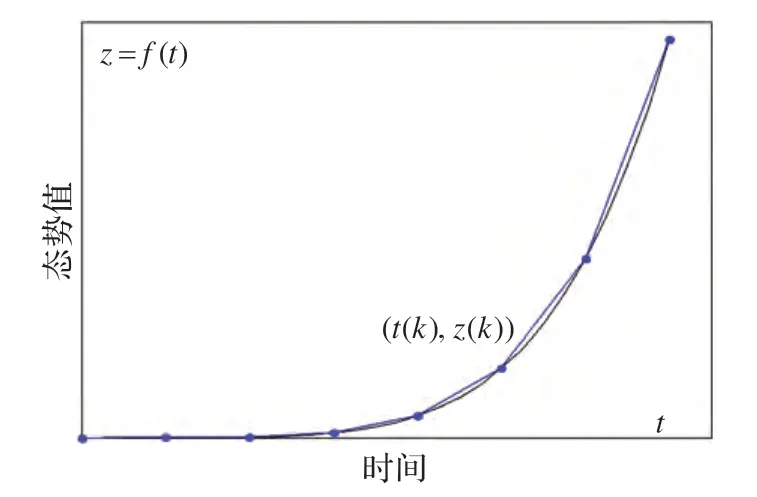
图3 曲线分段拟合

假设，F(i，n)表示从ti时刻开始的由采样点构成的折线子图。每条线段的斜率gk可表示为：

其中，zk表示tk时刻的态势值。依据式（6）可得预测曲线的斜率序列（Prediction Serial，PS）和实际曲线的斜率序列（Actual Serial，AS）。

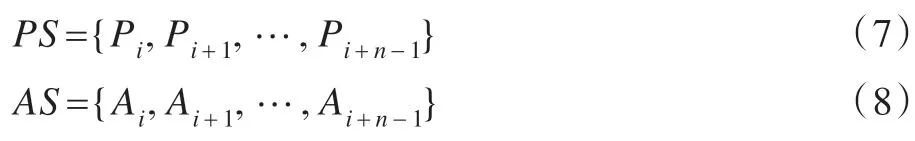
计算PS 与AS 转置的乘积，可得乘积向量MS={Mi，Mi+1，…，Mi+n-1}。即：

向量MS中的元素为正值表示预测曲线与实际曲线变化趋势相同，MS中的元素为负值表示预测曲线与实际曲线变化趋势相反。MS中的元素为正值的个数，m越大，表明预测曲线在大多数时间的变化趋势与实际曲线相似；反之，m越小，表明预测曲线在大多数时间的变化趋势与实际曲线相反。MS中正值的个数从某种意义上反映了预测算法对真实值的预测能力。

定义5趋势一致量TCA（Trend Consistent Amount）

预测序列的趋势一致量用向量MS中正值个数来表示。即：

其中，{∀Mi|Mi＞0}表示乘积向量MS中正值元素所构成的集合，|{ ∀Mi|Mi＞0} |为该正值集合的势，表示其中元素的个数。

定义6趋势拟合度TF（Trend Fitness）

预测曲线的趋势拟合度用预测序列与实际序列中趋势相同序列个数与序列的势之间的比率来表示。

其中，TCA表示乘积向量MS中正值个数，|PS|称为序列PS 的势，表示序列PS 中元素的个数。预测序列与实际曲线的趋势拟合度越高，说明预测算法的预测精确性高的可能性越大，因此在组合预测时应赋予其较高的组合权重；反之，在组合预测时为其分配较低的组合权重。在获得每个算法的趋势拟合度之后，对趋势拟合度进行归一化处理，可将其归一化结果作为其趋势拟合权重Tw（Trend Fitness Weight）。

2.3.2.3 基于信息熵的权重分配

信息熵标志着所含信息量的多少，是对系统不确定性程度的描述，可以用来衡量信息的不确定性程度[13]。对于一组在[0，1]内的且满足归一化的数据，信息熵可以衡量数据的集中程度。如果一个信息系统中n个不确定事件，记为x1，x2，…，xn，每个事件的发生概率记为p1，p2，…，pn，则信息熵的计算公式为：

预测序列中每个分段的相对误差构成相对误差序列（Absolute Percent Error Serial，EAPES）：

EAPES={EAPES1，EAPES2，…，EAPESn}

根据信息熵的含义，EAPES序列的信息熵越大，预测算法对态势真实值的拟合越趋于稳定，其对态势真实曲线的拟合能力越强。因此，能较好地反映预测算法对目标态势曲线的稳定、持续拟合能力。

定义7拟合稳定度FS（Fitness Stability）

拟合稳定度用MAPES 序列的信息熵来表示。定义如下：

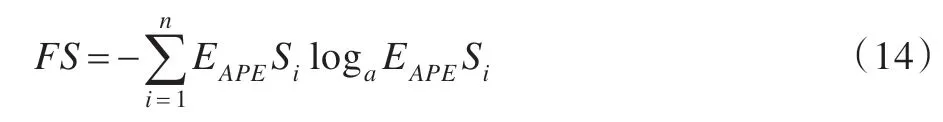
预测序列与实际曲线的拟合稳定度越高，说明预测算法的持续精确预测能力越高，因此，在组合预测时应赋予其较高的组合权重；反之，应为其分配较低的组合权重。

在获得每个算法的拟合稳定度之后，对拟合稳定度进行归一化处理，可将其归一化结果作为其拟合稳定性权重Sw（Fitness Stability Weight）。

2.4 基于证据理论的权重融合

证据理论通过对多源证据的融合，获得对命题的一致性描述，降低信息的不确定性[14-15]。在证据理论中，所有研究对象的全体称为一个识别框架Θ，证据理论的核心是Dempster合成规则[16]。

定义8Dempster合成规则

设识别框架Θ 的n个证据为(E1，E2，…，En)，其对应的基本信任分配函数为mi(i=1，2，…，n)，则n个证据组合后的信度分配函数为：

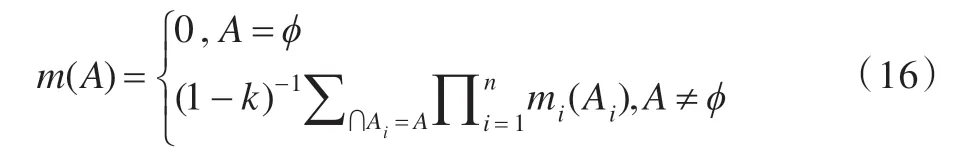
2.4.1Ew权重融合

Ewi是采样序列中第i个采样点计算的权重分配，n个采样点可获得n组权重分配。n个采样的权重分配可看作是n个专家为不同算法的信任赋值。因此，可以利用证据理论在不确定性问题处理上的优势，对n个权重序列进行合成，从而获得更为精确的Ew权重分配。

假设，二次指数平滑、BP 神经网络模型和ARIMA模型的预测值为P1，P2，P3，三种模型的权重分别为w1，w2，w3，识别框架Θ={P1，P2，P3}，采样序列的长度为n，则通过式（17）可将权值分配转化为信任分配：

将三种权值分配的结果转化为信任分配，可获得相对误差证据矩阵Ee：

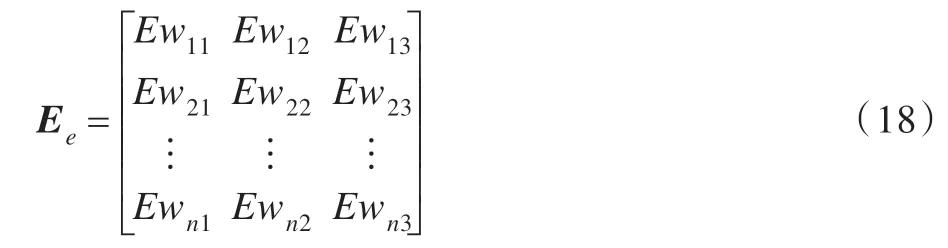
通过证据理论的组合公式（16）对矩阵Ee进行融合，可以获得更为精确的相对误差权值Ewc1、Ewc2、Ewc3。

2.4.2 三种权值分配方案的证据融合

依据相对误差、趋势拟合度和拟合稳定度可以为组合算法模型中的算法赋予不同的权值序列Ewc1，Ewc2，Ewc3、Tw1，Tw2，Tw3、Sw1，Sw2，Sw3。三种权值分配方案从不同的角度评价了子模型的预测精度。类似于Ew的处理，通过式（17）将三种权值分配结果转化为信任分配，可得组合权重证据矩阵Ec：

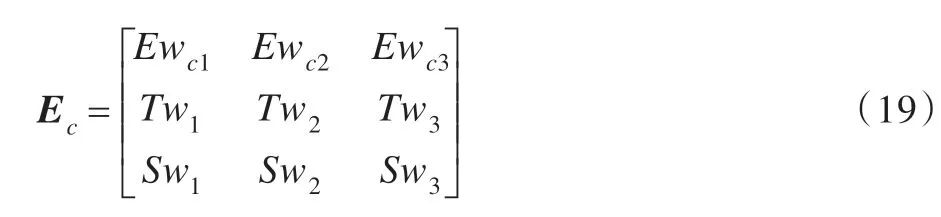
通过证据理论对证据矩阵Ec进行融合，可以获得更为精确的权重分配Fw=(mc1，mc2，mc3)。此时，组合预测结果可表示为：

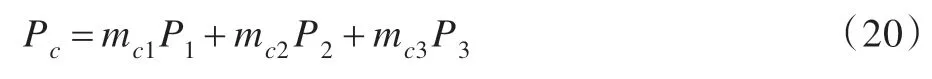
为了后续描述的方便，后文中将由各指标直接获取的权重称之为指标权重，将指标权重证据理论融合的结果称之为组合权重。

2.5 组合预测算法

图4 给出了基于SFM_ETO 的预测算法（SFM_ETO Algorithm，SFM_ETO_A）的伪码描述。

图4 基于SFM_ETO 的态势预测算法

2.6 优化演进算法

本文采用的相对误差、拟合一致度和拟合稳定度指标对刻画预测模型的性能具有一定的普遍性。但是，由于态势曲线的变化是不确定的，因此，在一些情况下，某些指标对态势曲线的表达会出现较大偏差，从而导致较差的预测精度。证据理论一般通过最大信任的方法做出决策，其信任值代表了对决策结果的支持程度。如果指标权重的决策结果与组合权重的决策结果一致，且预测结果达到精度阈值要求，则说明指标权重与精确预测之间具有强相关性。因此，可以利用这种相关性的强弱来表达指标的强弱程度。

定义9指标强度（Index Strength，IS）

假设进行了n次精确组合预测（达到设定的精度阈值），若依据某指标获得的权重分配与组合权重分配有m次保持一致，则该指标的指标强度可表示为：

指标的强度表示了对精确预测的支持程度。指标强度越高，该指标在组合模型中的地位越重要，可信程度越高；反之，该指标在组合模型中的地位越重要，可信程度越低。

定义10指标可信度（Index Confidence，IC）

指标强度的归一化结果称之为指标可信度。

指标可信度较好地刻画了预测指标对预测子模型的评价能力。态势预测模型的优化演进过程应弱化低可信指标的权重分配结果，尽可能地降低低可信指标的负面影响。在组合模型中，指标权重是以证据的形式进行组合的，Shafer 提出的证据折扣法可有效降低低可信证据在融合结论中的影响。因此，每次组合预测完成后，计算证据可信度，在新的预测周期中采用Shafer 的证据折扣法对指标权重进行优化调整。证据折扣法的表达式如式（23）所示。

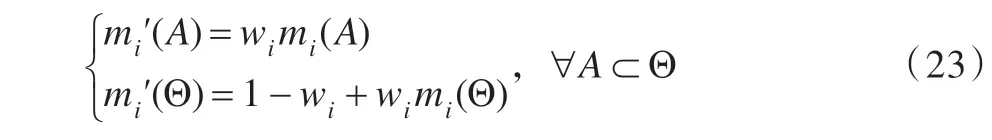
其中，w1，…，wi，…，wn表示证据i的权重，可用指标可信度来代替；mi(A)表示证据中焦元的信任度，可用指标权重代替。

图5 给出了优化演进算法（Optimization Evolution Algorithm，OEA）的伪代码描述。

图5 优化演进算法

3 实验仿真

本文在Matlab2013 下进行了仿真实验，对比本文模型与单预测模型和单指标组合预测模型在性能上的差异。单预测模型选取本文中的子模型：二次指数平滑、BP 神经网络和ARIMA。单指标组合预测模型选取文献[5]中Yan 提出的组合预测模型。实验数据为态势预测领域所使用的经典数据集HoneyNet[4]，选取2000 年12 月1 日到2001 年1 月31 日的数据作为预测样本。由于网络安全态势和网络告警具有正相关性，故本文直接以数据集中网络告警的统计值作为态势。由于在态势评估中，一般取[0，1]为态势的取值区间，因此，本文对所得态势值均作极值标准化处理[4]，处理结果如图6 所示。

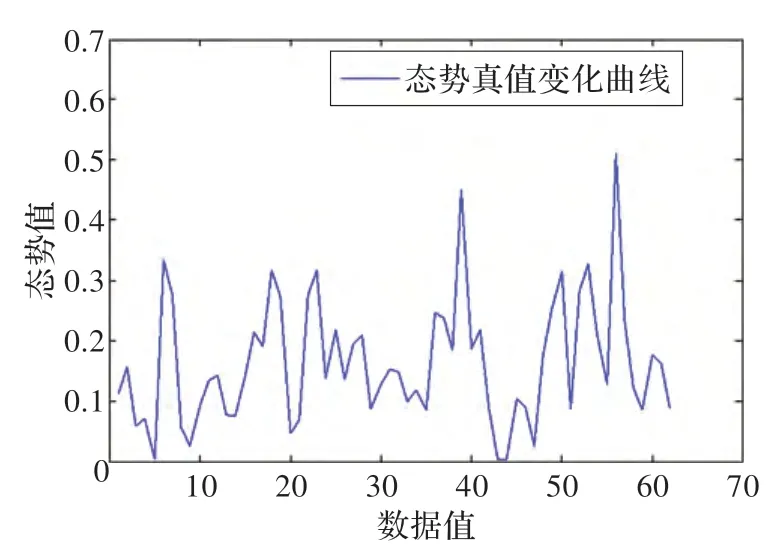
图6 态势真值

3.1 实验设置

设置预测输入窗口LWin=25；为了检测输出窗口对预测精度的影响，预测输出窗口取较大值LWout=5。即，首先，取前25 个数据作为样本进行训练，获得各子模型的合理参数配置；然后，子模型对26～30 个数据进行态势预测，获得子模型的评价，并利用证据理论进行权重分配；最后，利用组合模型对31～35 个数据进行态势预测，并将其结果与典型预测模型的结果进行比较。

实验中的参数设置如表1 所示。

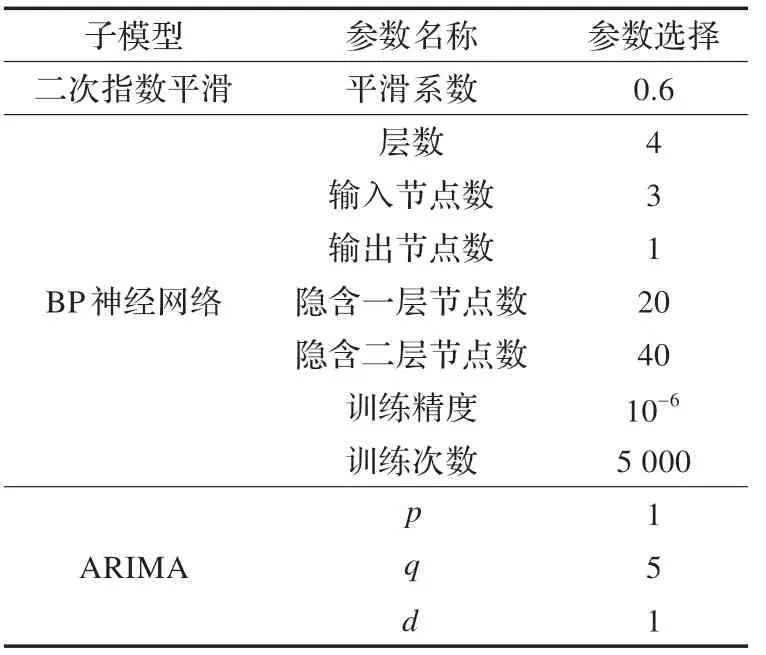
表1 实验参数设置

3.2 实验结果

前25 组态势数据的训练结果如表2 所示。

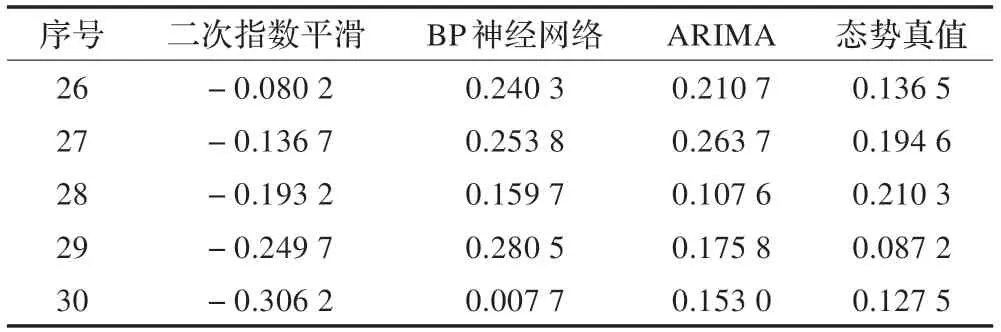
表2 训练获取的单模型预测结果

依据式（5）、（12）、（15）和（19）可得组合权重矩阵为：

利用证据理论对Ec进行证据融合，可得最终的组合预测模型为：

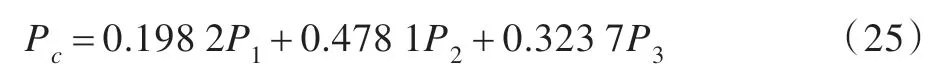
利用该组合模型对第31～35 组数据分别进行组合预测和单模型预测。不同预测模型的实验对比如图7～图9 和表3 所示。

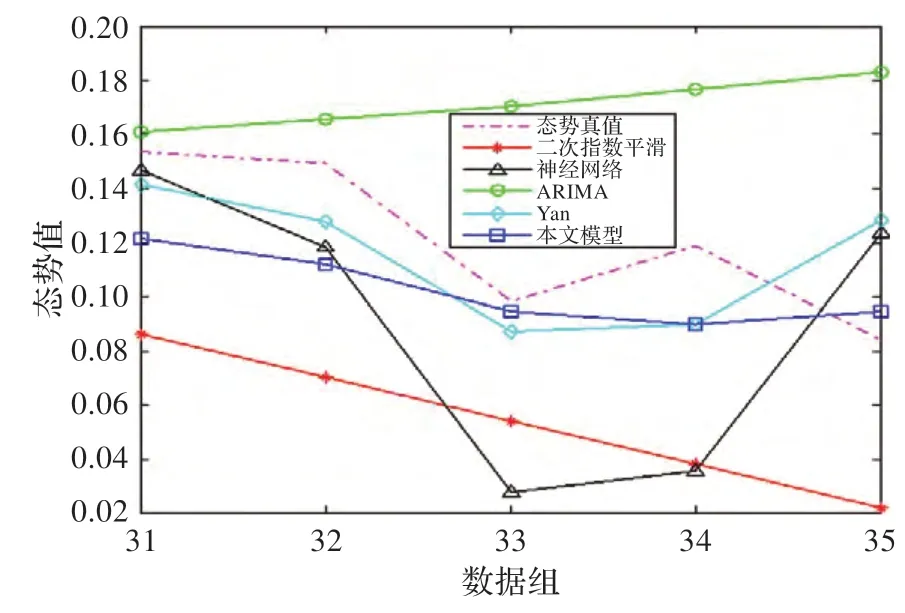
图7 不同预测模型的预测结果对比

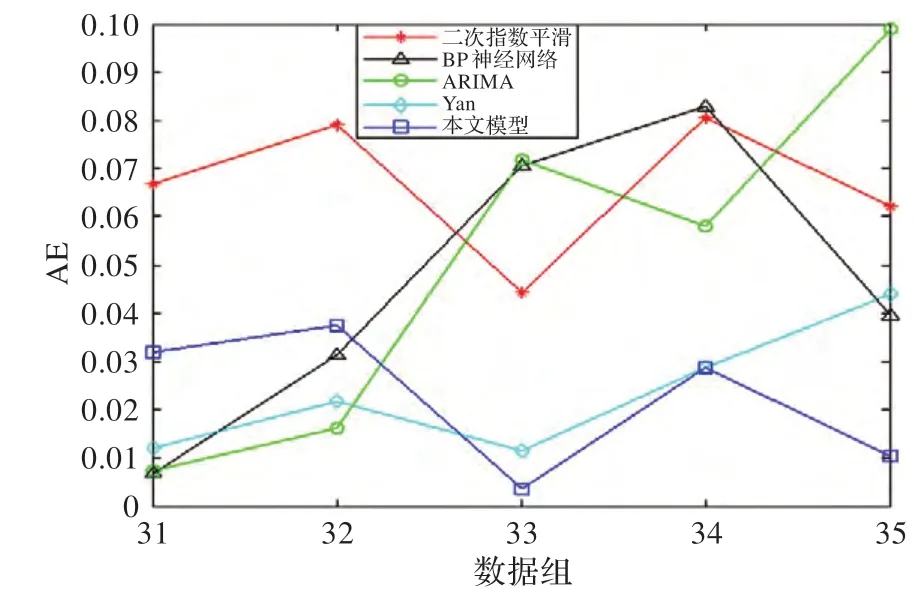
图8 不同预测模型的AE 对比

3.3 实验分析

从图7 中可以看出，本文预测模型与Yan 预测模型的拟合曲线在变化上更趋近于实际的态势曲线。图8和图9 中的绝对误差AE 和绝对相对误差APE 对比表明，在预测窗口较大时，单预测模型的误差变化起伏较大，随着预测步长的增加，预测误差上升较快，而本文模型和Yan 模型在误差稳定性上的表现要优于单预测模型，本文预测模型的误差变化曲线相对更为稳定，主要原因是本文模型在组合权重确定时考虑了曲线趋势变化特征和稳定性特征。表3 中的平均绝对误差MAE 和平均相对误差MAPE 的对比结果表明，本文模型的误差最小，分别为MAE=0.022 4，MAPE=17.26%，其预测精度比Yan 模型高4.91%。

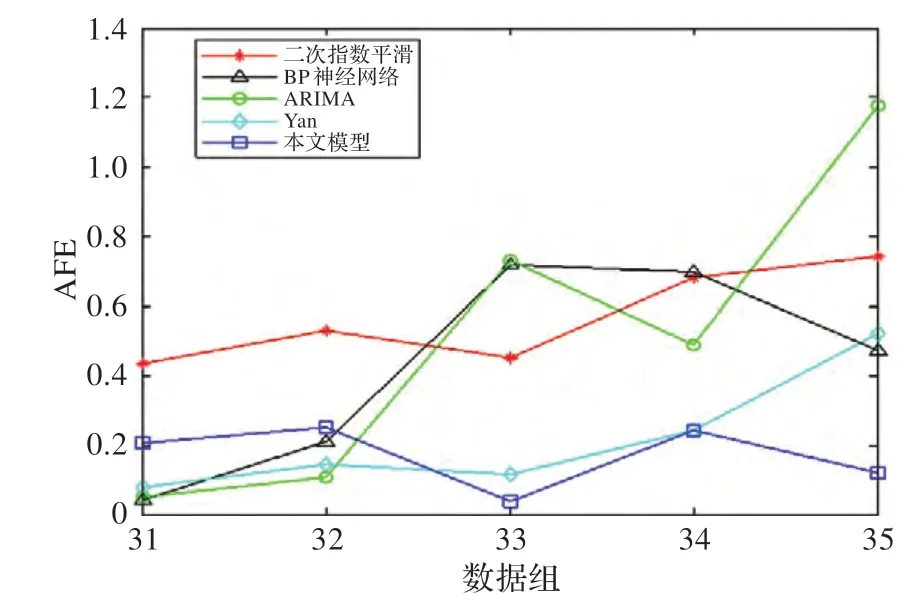
图9 不同预测模型的APE 对比

表3 不同预测模型的MAE 和MAPE 对比

4 结束语

本文研究了多模型态势组合预测问题。通过对现有典型预测方法的分析，提出了一种基于证据理论优化的态势组合预测方法。Matlab 实验仿真结果表明，本文的组合预测模型能够依据态势曲线的变化特征对组合权重进行动态调整，模型的适应性和稳定性较好，且预测精度明显高于典型预测模型。

本文提出的预测模型组合方法和优化演进方法提供了对多个单预测模型进行组合、优化以实现更精确预测的框架，在预测子模型选择上并未刻意寻求性能最优的子模型。因此，SFM_ETO 模型的预测子模型可进一步扩展，或采用性能更优的预测子模型替代本文的子模型，以获得更好的预测效果。如何针对具体的态势类型，如性能态势、传输态势、安全态势等，改进上述模型的子模型构成是下一步工作的重点。

[1] 王慧强，赖积保，胡明明，等.网络安全态势感知关键实现技术研究[J].武汉大学学报，2008，33（10）：995-998.

[2] 李松，刘力军，刘颖鹏.改进PSO 优化BP神经网络的混沌时间序列预测[J].计算机工程与应用，2013，49（6）：245-248.

[3] 程绪超，陈新宇，郭平.基于改进Elman 网络模型的软件可靠性预测[J].通信学报，2011，32（4）：86-93.

[4] 李彩虹.两类组合预测方法的研究与应用[D].兰州：兰州大学，2012.

[5] Yan Bin，Yu Haibo，Gao Zhenwei.A combination forecasting model based on IOWA operator for dam safety monitoring[C]//2013 Fifth International Conference on Measuring Technology and Mechatronics Automation（ICMTMA），2013：5-8.

[6] Xu Yabo，Wang Tong，Song Bingxue，et al.Forecasting of production safety situation by combination model[J].Procedia Engineering，2012，43（2012）：132-136.

[7] Zheng Jianhong，Qiao Jinyou.Application and evaluation on combination forecasting model based on information entropy and Shapley value[C]//2011 International Conference on Consumer Electronics，Communications and Networks（CECNet）.IEEE，2011：1990-1993.

[8] Martins V L M，Werner L.Forecast combination in industrial series：A comparison between individual forecasts and its combinations with and without correlated errors[J].Expert Systems with Applications，2012，39（13）：11479-11486.

[9] 于静，王辉.基于组合模型的网络流量预测[J].计算机工程与应用，2013，49（8）：92-95.

[10] Rodrigues L R L，Doblas-Reyes F J，dos Santos Coelho C A.Multi-model calibration and combination of tropical seasonal sea surface temperature forecasts[J].Climate Dynamics，2013，4（1）：1-20.

[11] Huwiler M，Kaufmann D.Combining disaggregate forecasts for inflation：The SNB's ARIMA model[R].[S.l.]：Swiss National Bank，2013.

[12] Li G，Shi J，Zhou J.Bayesian adaptive combination of shortterm wind speed forecasts from neural network models[J].Renewable Energy，2011，36（1）：352-359.

[13] 寻二辉，任趁妮.一种改进的冲突证据融合方法[J].计算机科学，2012，39（11）：31-38.

[14] Yee Leung，Ji Nannan，Ma Jianghong.An integrated information fusion approach based on the theory of evidence and group decision-making[J].Information Fusion，2012，23（2）：1-13.

[15] 陈金广，张芬.多证据源冲突的组合度量方法[J].计算机工程与应用，2013，49（9）：222-227.

[16] Xu Xiaobin，Feng Haishan.An information fusion method of fault diagnosis based on interval basic probability assignment[J].Chinese Journal of Electronics，2011，20（2）：255-260.