基于主成分-正则化极限学习机的超高密度电法非线性反演

江沸菠, 戴前伟， 董莉

1 中南大学地球科学与信息物理学院， 长沙 410083 2 湖南师范大学物理与信息科学学院， 长沙 410081 3 湖南涉外经济学院信息科学与工程学院， 长沙 410205



基于主成分-正则化极限学习机的超高密度电法非线性反演

江沸菠1,2, 戴前伟1*， 董莉1,3

1 中南大学地球科学与信息物理学院， 长沙 410083 2 湖南师范大学物理与信息科学学院， 长沙 410081 3 湖南涉外经济学院信息科学与工程学院， 长沙 410205

超高密度电法是一种新的地球物理探测技术，它通过多通道数据采集和多装置数据联合反演，极大地提高了电法勘探的成像精度.本文提出一种主成分-正则化极限学习机(PC-RELM)非线性反演方法，该方法针对超高密度电法所获取的高维勘探数据进行反演建模，通过随机设定隐层参数来简化模型的学习过程，通过主成分分析方法来进行高维数据降维，最后引入正则化因子提高反演模型的泛化能力.论文给出了超高密度电法的原理、样本构造方法和非线性反演流程，使用交叉验证方法获得了优化的隐节点数目和正则化参数，构造了优化的反演模型.通过两个经典的超高密度模型的反演结果表明，该方法能够较好地解决超高密度电法反演的高维数据非线性建模问题，能够弥补单一装置数据反演的不足，同时相较其他的非线性反演方法(ELM, BPNN和GRNN)具有更加准确的反演结果.

超高密度电法； 正则化； 极限学习机； 主成分分析

1 引言

超高密度电法是高密度电法在采集方式上的改进，其勘探原理与常规的电法相同，均以岩矿石的电性差异为基础，通过观测和研究人工建立稳定电场的分布规律来解决水文、环境和工程地质问题.然而在传统的高密度电法勘探中，不同排列类型的装置具有不同的分辨率和勘探深度，在相同的地质结构上，不同装置的视电阻率伪截面有着较大的不同.为了重构更加精确的地下地质结构，改进传统的电法勘探采集数据的方式，通过多装置数据融合来提高电阻率成像的分辨率成为了电阻率反演的一个重要方向.Stummer等(2004)较早进行了复杂电法数据采集的实验，该实验给出了一种包含标准装置数据和非标准装置数据的综合电法数据采集方法，可以在多电极系统中获取更多的数据以提高电阻率成像的精度(Stummer et al., 2004).Athanasiou等 (2007)根据不同装置数据的反演特点，提出了一种混合权重的综合反演方法.该方法通过附加权重因子的方式来综合偶极-偶极，单极-偶极，温拿-斯伦贝格，温拿装置的反演结果，从而充分利用各种装置反演中的有效信息，得到更加可靠的地质模型(Athanasiou et al., 2007).Zhe等 (2007)提出了一种多通道，多电极的电阻率采集系统.该系统能够提供一种“泛装置”的数据采集方法，通过提高采集电阻率数据的数量来获取更高精度的反演成像质量，该方法在国内也称为“超高密度电法”或“超高密度电阻率成像”(Zhe et al., 2007).

目前，超高密度电法已在国内多个工程项目中得到了广泛的应用(冯德山等, 2014; 雷旭等, 2009)，但是其反演方法主要沿用传统高密度电法中的2.5维线性或拟线性反演方法(钟韬, 2008)，存在着依赖初始模型、易陷入局部极值、偏导数矩阵求解困难等问题.完全非线性反演方法是电阻率法反演领域新的研究方向，Neyamadpour等(2010)研究了人工神经网络在反演三维直流电阻率成像数据中的应用.他使用有限单元法生成偶极-偶极装置的正演数据，并用其来进行神经网络的训练；针对BP神经网络的不足，他通过优化网络结构，使用动量因子来改善神经网络的反演性能，取得了较好的反演结果(Neyamadpour et al., 2010)；Shaw和Srivastava (2007)评估了粒子群优化算法在地球物理反演中的应用能力，实现了粒子群优化算法对DC数据，IP数据和MT数据的反演(Shaw and Srivastava, 2007). Sharma (2012)使用快速模拟退火算法来解释一维直流电测深数据，并通过概率密度函数来评估所获得的反演模型(Sharma, 2012)；Liu等(2012)提出了一种可控变异方向的遗传算法，该方法使用三维有限元法进行正演建模，在遗传算法的目标函数中加入平滑约束和不等约束，通过该算法在解空间中搜索模型参数，大大地提高了遗传算法的求解速度，并成功地应用于广州地铁的地下勘探中，其反演结果与钻孔资料基本吻合(Liu et al., 2012).

以上非线性方法均在电阻率反演中得到了较为广泛的应用，但应用至超高密度电法反演中均存在不足，一方面，粒子群优化、模拟退火、遗传算法等蒙特卡洛类算法的原理是以一定的规则引导反演算法在全局解空间内搜索最优解，通过反复调用正演算法来评估解的质量，并最终收敛于全局最优解，但由于超高密度电法的解空间规模大、正演算法计算时间长，该类方法的计算效率很低；另一方面，神经网络等机器学习类方法的原理是通过正演算法来产生一系列用于学习的样本，然后使用一种机器学习模型来对样本进行学习，通过学习来调整模型的结构和参数，并最终产生能够正确解释观测数据的反演模型，但由于超高密度电法学习样本的维度大，参数多，其训练过程往往难以收敛并极易陷入局部极值.因此寻找一种合适的非线性反演方法进行超高密度电法数据的反演和解释势在必行.

极限学习机是一种具有高效学习性能的机器学习新算法，已广泛应用于回归与分类(Huang et al., 2012; Luo et al., 2014)、图像识别(Mohammed et al., 2011; Zong and Huang, 2011)和决策支持(Sun et al., 2008)等领域.本文针对超高密度电法反演的高维、非凸及非线性特征，提出了一种主成分-正则化极限学习机算法，该方法通过随机设定隐层参数来简化反演模型的学习过程，通过主成分分析对超高密度电法采集的电位差数据进行降维，提高了反演算法的计算效率.同时极限学习机的Moore-Penrose广义逆计算过程和正则化因子的引入从理论上保证了反演算法的全局最优和泛化能力，较好地解决了超高密度电法的局部收敛问题.本文还给出了超高密度电法的有限体积正演方法及非线性反演模型的设计流程，并通过两个经典的超高密度电法模型反演验证了本文算法的有效性.

2 超高密度电法的原理

传统的电阻率成像勘探中，由于受到不同装置电极排列规律的限制，在同一条件下，用不同的装置进行数据采集实验所得到的原始视电阻率数据图和反演后的电阻率图均不相同.而超高密度电法实际上是一种基于“泛装置”的阵列勘探方法，虽然它仍沿用高密度电法勘探的电极阵列，但突破原有程式化单装置模式的束缚，不再分装置方式观测和反演.以30个电极为例，4极泛装置超高密度电法的工作过程如下：将测线上排列的30个电极分为奇数组15个电极(1, 3, 5,…,29)和偶数组15个电极(2, 4, 6,…,30)2组，然后在这两组电极中各选取一个作为供电电极A和B，在一次通电过程中同时测量其他电极(27个N极)相对于某一电极M的电位差，就可得到27个电位差.奇数组15个电极和偶数组15个电极互相配对(全排列)作为供电电极，即一条测线上的所有电极有15×15种AB电极排列，每种排列可同时采集27个电位差数据，所以总的数据量为15×15×27=6075，远大于传统的高密度电法所获取的数据量.超高密度电法的装置示意图如图 1所示.

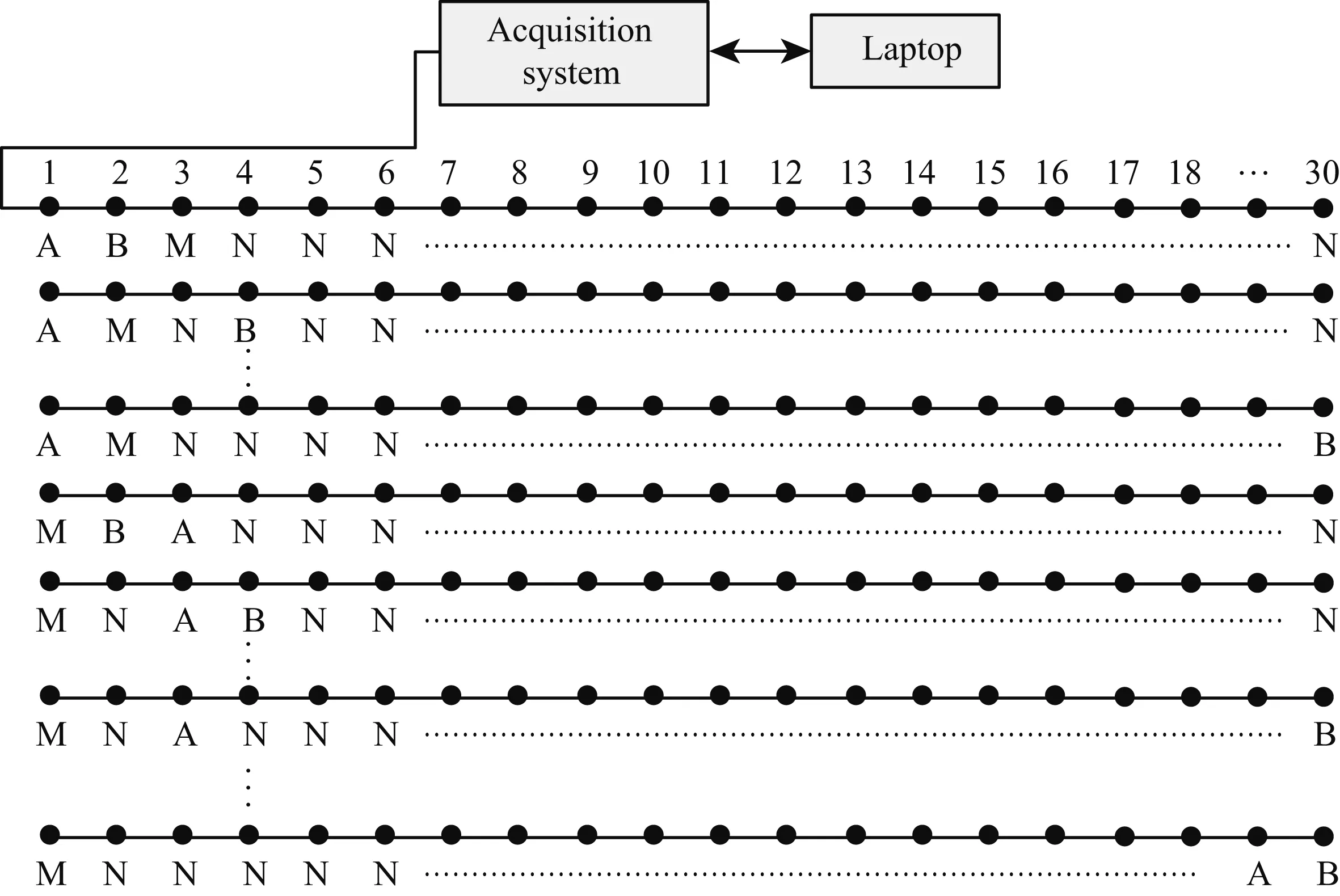
图1 超高密度电法(30电极)的装置示意图Fig.1 Ultra-high density resistivity method equipment (including 30 electrodes)

本文以上述装置为基础，采用有限体积法进行2.5维电阻率成像的正演计算(Pidlisecky and Knight, 2008)，得到各测量电极的电位矩阵，结合图1中超高密度电法4极装置的电极坐标矩阵，即可求解各MN电极之间的电位差，从而实现超高密度电法4极装置的2.5维正演数值模拟，为进一步研究超高密度电法的非线性反演提供支持.同时为测试反演算法的稳定性和泛化能力，在正演数据中加入了3%的随机噪声.

3 极限学习机理论

3.1 标准极限学习机

极限学习机(Extreme Learning Machine, ELM)是Huang提出的一种机器学习新方法(Huang et al., 2006).该方法以单隐层前馈神经网络为模型，对网络的输入权值和偏置进行随机赋值，并在最小二乘准则的基础之上，利用Moore-Penrose广义逆计算输出权值，因此克服了基于梯度下降学习理论的学习机器的固有缺陷，具有收敛迅速、不易陷入局部极值等优点，适合对高维输入输出的超高密度电法反演问题进行建模.标准的极限学习机工作原理如下.

对于给定的训练样本集{(xi,ti)|i=1,2,…,N}，xi=(xi1,xi2,…,xin)T∈Rn，ti=(ti1,ti2,…,tim)T∈Rm.具有L个隐节点并采用激活函数g的单隐层前馈神经网络的数学模型可描述为

j=1,2,…,N,

(1)

式中wi=(wi1,wi2,…,win)T为第i个隐节点与输入节点间的权值向量，βi=(βi1,βi2,…,βi m)T为第i个隐节点与输出节点间的权值向量，bi为第i个隐节点阈值.

为了最小化极限学习机的目标函数

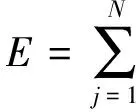
‖oj-tj‖,

(2)

传统的梯度下降学习算法主要采用迭代的方式来更新网络参数，其迭代过程为

(3)

式中W为参数(w,β,b)的集合，η为学习率.但该方法存在收敛缓慢，容易陷入局部极值等问题.

极限学习机通过寻求最优的网络参数以使得目标函数最小，即

‖H(w1,w2,…,wL,b1,b2,…,bL,x1,x2,…,xN)β-T‖,

(4)

因此极限学习机的网络训练过程可等效为一个非线性优化问题，当激活函数无限可微时，网络的输入权值和隐节点阈值可随机赋值，则(4)式等效为

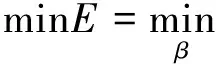
‖H(w1,w2,…,wL,b1,b2,…,bL,x1,x2,…,xN)β-T‖.

(5)

(6)

式中H+为H的Moore-Penrose广义逆矩阵.

3.2 主成分-正则化极限学习机

根据标准ELM算法的基本理论可知，ELM的优点主要体现为以下两点：(1)ELM通过随机赋值的方式指定了隐层参数，仅需对神经网络的输出层参数进行学习和调整，极大地提高了神经网络的学习速度；(2)ELM通过求解广义逆的方式来得到输出层参数的最小范数二乘解，避免了传统梯度算法的局部极值问题.相较于传统的电阻率成像，超高密度电法的反演数据量更大，需要更加复杂的神经网络隐层结构进行非线性映射，而复杂的隐层结构必然导致学习参数的增加以及学习过程的缓慢，同时也更容易产生局部最小值.因此ELM从理论上解决了超高密度电法反演的主要问题，适合进行超高密度电法的非线性反演.

然而标准的ELM算法主要存在两个问题：(1)输出层参数求解采用Moore-Penrose广义逆矩阵的方式，容易导致过拟合现象，影响了ELM的泛化能力；(2)隐节点的个数与学习精度直接相关，在求解复杂的应用问题时，ELM网络的结构往往过于庞大(Luo et al., 2014).为解决过拟合问题，Huang在标准的ELM中引入了正则化参数(Huang et al., 2011)，以增强ELM的稳定性和泛化能力，此时极限学习机的目标函数为

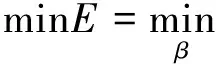
‖Hβ-T‖+λ‖β‖,

(7)

式中λ为正则化参数，此时的β为

(8)

正则化ELM通过引入正则化参数，提高了ELM在小样本学习条件下的泛化能力，符合超高密度电法反演中训练样本的构造特点，然而由于超高密度电法采用“泛装置”进行数据采集，采集的电位差无法根据装置系数转化为视电阻率，反演模型的输入为采集的所有电位差，因此其输入维数过高，以30个电极的超高密度电法装置为例，其输入维数就达到了6075，这对于任何机器学习方法而言都需要庞大的结构对其进行学习，降低了反演算法的效率和可靠性.主成分分析(Principal Component Analysis, PCA)和机器学习模型结合是对高维数据进行机器学习的一种新方法(Ghosh-Dastidar et al., 2008; Ravi and Pramodh, 2008; Reddy and Ravi, 2013).本文结合PCA和正则化ELM技术，提出了一种主成分-正则化ELM(PC-RELM)反演模型，其基本结构如图 2所示.

PC-RELM反演模型分为四层，其中输入层用于采集的超高密度电法的电位差数据输入；PCA层用于对高维电位数据进行降维，按照预先设定的阈值选择合适数量的主成分，从而简化极限学习机的隐层结构；隐层主要用来对超高密度电法的电位差数据和反演的模型参数之间的非线性关系进行学习和拟合；输出层则对反演的模型参数进行输出.本反演模型通过主成分分析进行特征提取和降维，避免了在高维特征空间运算时存在的“维数灾难”问题，适合超高密度电法采集的高维数据在进行反演解释时的ELM结构设计.因此本文采用基于主成分-正则化的ELM进行超高密度电法非线性反演的建模.

图2 含PCA层的ELM结构Fig.2 The architecture of ELM with PCA layer

4 反演建模

本章主要针对超高密度电法进行极限学习机非线性反演的理论研究，其获取样本的正演模型参数设置如下：测量电极为30个，极距为1 m，一条测线上共采集6075个电位差数据.

4.1 样本构造

考虑到极限学习机样本学习的流程与神经网络类似，通过借鉴神经网络反演中对样本的构造方式来完成极限学习机的反演建模.针对电阻率反演的神经网络建模，目前的文献中主要有两种方法，一种是使用视电阻率的水平位置、垂直位置和视电阻率值为输入节点，对应位置的真电阻率值为输出节点，将每次测量的所有数据点设为一个数据集进行训练(Neyamadpour et al., 2009).该方法的特点是神经网络的结构简单、训练迅速.但视电阻率和真电阻率一一对应，无法充分反映视电阻率是电场作用范围内地下电性不均匀体的综合反映这一视电阻率的本质特征；另一种是将所有测量的视电阻率作为输入节点，所有模型参数作为输出节点(Ho, 2009).该方法建立的神经网络输入输出节点数量大，且隐含层结构复杂，如此大规模的神经网络不仅需要通过大量的时间来进行训练和确定隐含层的最优节点数、而且训练和测试需要更多的样本数据.根据超高密度电法的工作原理可知，超高密度电法没有特定的装置，所以无法根据装置系数计算视电阻率，只能使用电位差作为极限学习机的输入，因此本文只能采用第二种方法进行极限学习机的建模，其中极限学习机的输入维度为采集的超高密度电位差数据6075，输出维度为地电模型有限体积法正演网格化后的模型参数数目2880.训练样本和测试样本的构造如图 3所示.

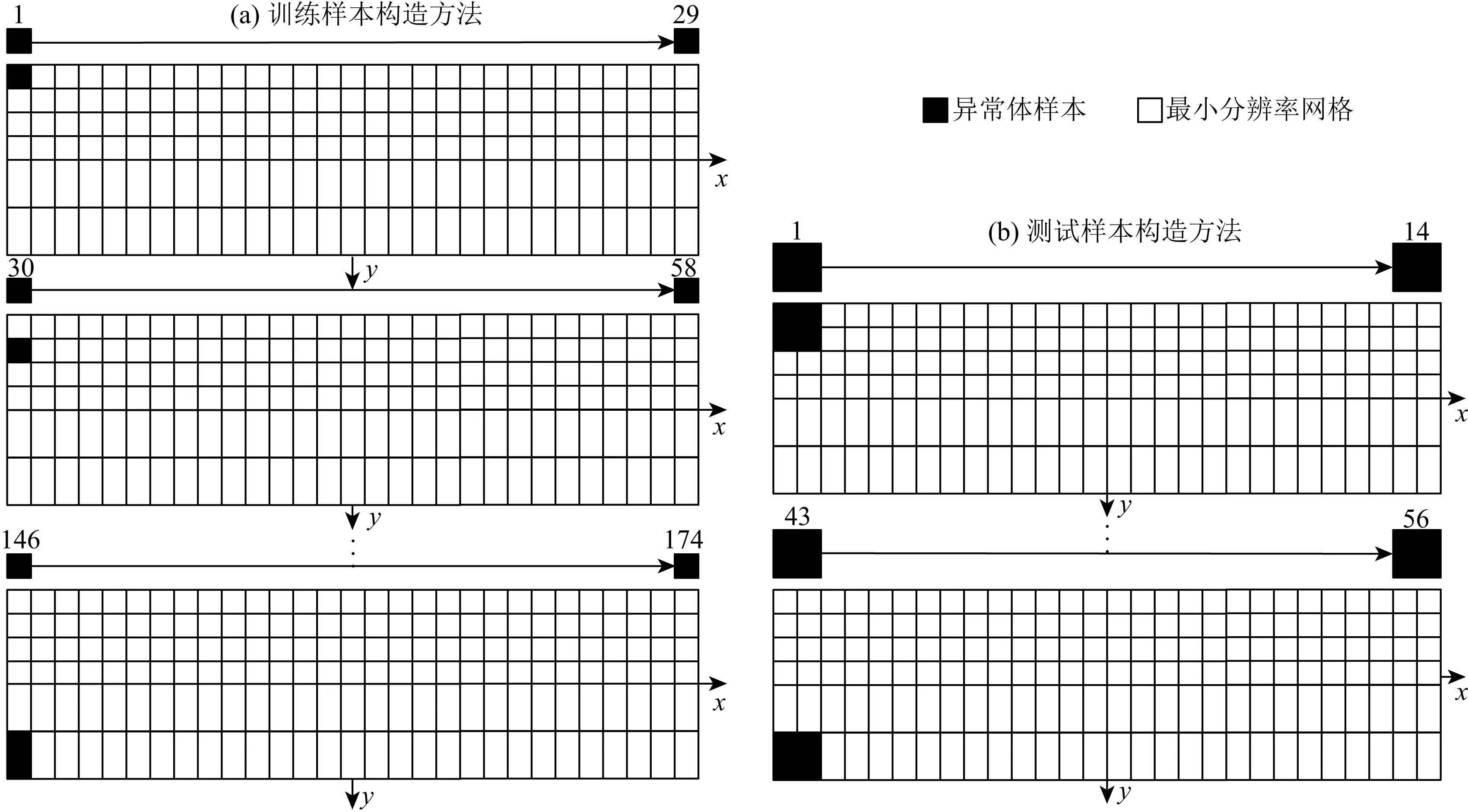
图3 ELM训练样本及测试样本构造Fig.3 The generation of training data sets and testing data sets for ELM

由图3可知，在模型空间上按照测量电极间隔划分构造样本的网格，x轴的网格间隔为1 m，y轴的网格间隔随着深度的增加逐渐递增，本文中y轴的网格间隔依次为1 m,1 m,1 m,1 m,2 m,2 m.然后使用最小分辨率的单异常体遍历模型空间，求解不同位置时的正演数据获得训练样本.同理，参照探测目标大小建立测试异常体，使用测试异常体遍历模型空间，求解不同位置时的正演数据获得测试样本.测试样本不参加训练，仅用来检测算法的泛化能力.

4.2 PCA 降维

Ho(2009)采用上述样本构造方法进行了简单的三维电阻率成像神经网络反演的样本构造.然而该方法直接应用于超高密度电法反演存在两点不足：(1)超高密度电法反演模型的输入为采集的所有电位差，输出为全部模型参数，因此其输入输出的维数过高；(2)采用遍历模型空间产生训练和测试样本的方法，在电极数较多时将产生大量的训练和测试样本.以上缺点直接影响了极限学习机进行非线性建模时的计算效率和稳健性.

虽然在样本构造阶段超高密度电法为机器学习模型提供了大量的高维特征数据和样本，但是这些高维特征数据的特征中存在着大量与目标异常体无关的特征和噪声，同时特征间存在着强列的冗余，因此本文在进行极限学习机反演建模前首先对超高密度电法产生的高维特征数据进行降维处理.针对超高密度电法采集的电位差数据，本文采用PCA层对高维特征数据进行降维.PCA降维的Pareto图如图4a所示，从图4a可知，前7个主成分已经包括了95%左右的原始数据信息，一般情况下只要大于7个主成分，均能够较好地描述超高密度电法所产生的高维特征数据.为了进一步确定降维的主成分个数，仿真了极限学习机随维度增加的训练误差变化曲线，如图4b所示.从图4b可知，在初始主成分较少的情况下，由于降维后的样本无法充分反映高维特征数据的相关信息，极限学习机的训练误差相对较高；随着维度的增加，所选主成分所包含的高维数据特征更加丰富，极限学习机的训练误差迅速下降，到达19维时开始逐渐稳定，同时由Pareto图可知，19个主成分已经包括了99%以上的原始信息，因此为了尽可能地保留高维数据的原始特征，同时兼顾ELM的反演效率，选择前19个主成分作为降维后的输入训练样本.

4.3 参数寻优

在正则化极限学习机学习的过程中，有三个参数影响ELM的学习和反演性能，它们分别是激活函数类型、隐节点个数和正则化参数.因此为构造优化的ELM反演模型，需要对激活函数类型、隐节点个数和正则化参数进行优选.考虑到激活函数类型对ELM的直接影响，优先对激活函数的类型进行选择.常见的ELM激活函数列举如下(Fernández-Navarro et al., 2011)：

(1) Sigmoidal function: Sigmoid(n)=1/(1+exp(-n)).

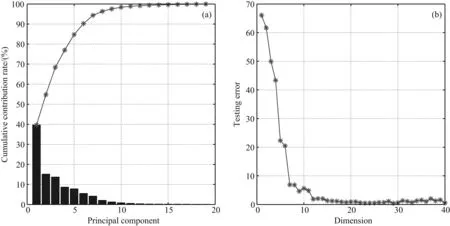
图4 超高密度电法电位数据主成分降维(a)Pareto图；(b)测试误差曲线.Fig.4 PCA dimensionality reduction for the potential data of ultra-high density resistivity method(a) Pareto Chart; (b) Testing error curve.

(2) Sine function: Sine(n)=(ein-e-in)/2i.

(3) Hard-limit transfer function: Hardlim(n)=1 ifn≥0; =0, otherwise.

(4) Triangular basis function: Tribas(n)=1-abs(n) if -1≤n≤1; =0, otherwise.

(5) Radial basis function: Radbas(n)=exp(-n2).

在不同的激活函数下，选择隐节点个数L和正则化参数λ的方法是让L和λ在一定范围内进行取值，在不同的L和λ参数下利用交叉验证(Cross Validation, CV)的方式进行训练，并将取得验证误差最低的那一组L和λ作为ELM的最佳参数.

CV是用来验证分类器性能的一种统计分析方法，基本思想是把在某种意义下将原始数据(dataset)进行分组，一部分作为训练集(train set)，另一部分作为验证集(validation set).其方法是首先用训练集对模型进行训练，再利用验证集来测试训练得到的模型，以得到的拟合误差作为评价模型的性能指标.采用交叉验证的思想可以有效地避免过学习和欠学习状态的发生，最终得到较为理想的拟合模型.本文采用K-CV的方式进行交叉验证，将原始训练数据均分为K组，将每个子集数据分别做一次验证集，同时其余的K-1组子集数据作为训练集，这样会得到K个模型，用这K个模型最终的验证集的验证误差的平均数作为此K-CV下拟合模型的性能指标.综合考虑参数寻优的时间和性能，通过凑试法本文设置K=5，L=[1,2,…,76]，λ=[2-6,2-5.5,…,25.5,26].最后分别求解在不同激活函数下，L和λ的归一化误差曲面如图 5所示.为便于显示，λ在图 5中取log2对数.

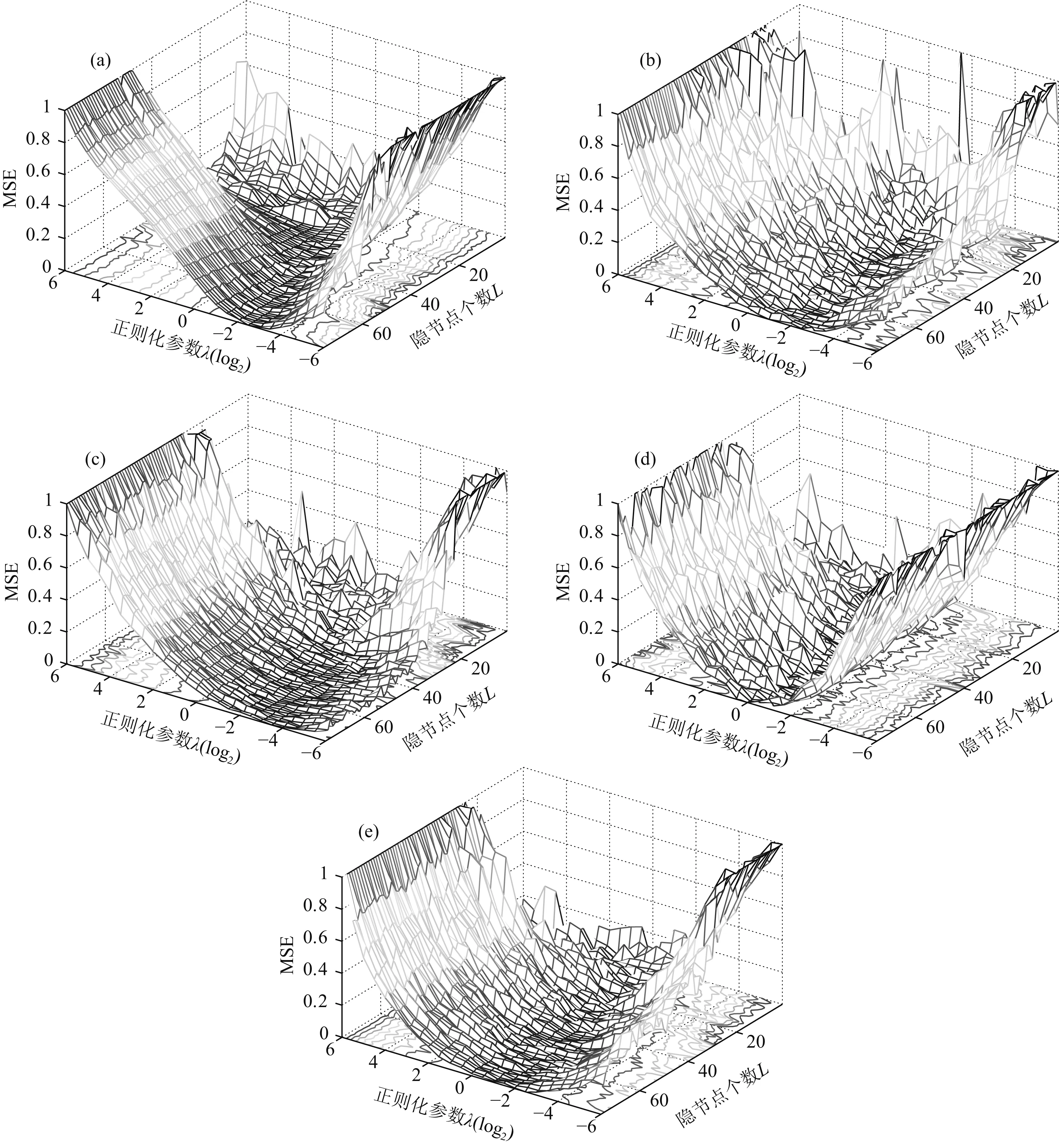
图5 不同激活函数下隐节点数目和正则化参数变化的归一化误差曲面(a) Sigmoid; (b) Sine; (c) Hardlim; (d) Tribas; (e) Radbas.Fig.5 Normalized error surface for hidden unit number and regularization factor value in the transformed space with different activation functions

表1进一步给出了不同激活函数下，最优L和λ参数的训练误差、测试误差和交叉验证计算时间.其中交叉验证计算时间的运行环境如下：CPU为Core(TM)i5-2450，内存为2GB，操作系统为Windows XP SP4.

由图5可知，虽然不同激活函数的误差曲面各异，但随着隐节点数目的增加和正则化参数的减小，交叉验证的误差曲面均开始下降，并逐渐收敛于某一特定区域，该现象表明：(1)随着隐节点数量的增加，使得ELM的隐层结构趋于复杂，非线性学习能力增强，数据拟合能力增加；当隐节点数目过低时(低于20时)，ELM的工作不稳定，误差曲面存在一定的振荡；(2)随着正则化参数的减小，ELM在学习过程中更加偏重于拟合误差，因此误差曲面逐渐下降，但当下降到一定程度时，为保证泛化能力，在交叉验证下，ELM模型的验证误差开始逐渐上升；(3)如果隐节点数量过大，则会产生过拟合；同理，如果正则化参数过小则会产生过约束，因此误差曲面最终收敛于隐节点较大和正则化参数较小的某一特定区域，获得了拟合精度和泛化能力的较好均衡；(4)相较于其他激活函数，Sigmoid函数的误差曲线更为平滑，表明在建模的过程中，ELM的输出随参数的变化更加稳定；其他激活函数由于ELM隐层参数指定的随机性，在收敛过程中均出现了不同程度的振荡.由表1可知，Sigmoid函数在参数L=68,λ=0.0625时取得了最低的交叉验证误差，建模性能最佳，同时几种激活函数的交叉验证计算时间相当，没有太大的差别.综上，本文采用Sigmoid激活参数进行ELM反演建模，其隐节点个数和正则化参数分别设置为68和0.0625.

4.4 反演流程

通过以上的研究和分析，使用PC-RELM反演超高密度电法数据的基本步骤如下：

(1)初始化电极数目、电极距等正演参数和PC-RELM反演参数；

(2)使用有限体积法正演产生电位数据；

(3)根据超高密度泛装置生成电极矩阵，并由电极矩阵和电位数据计算超高密度电法的采集电位差数据；

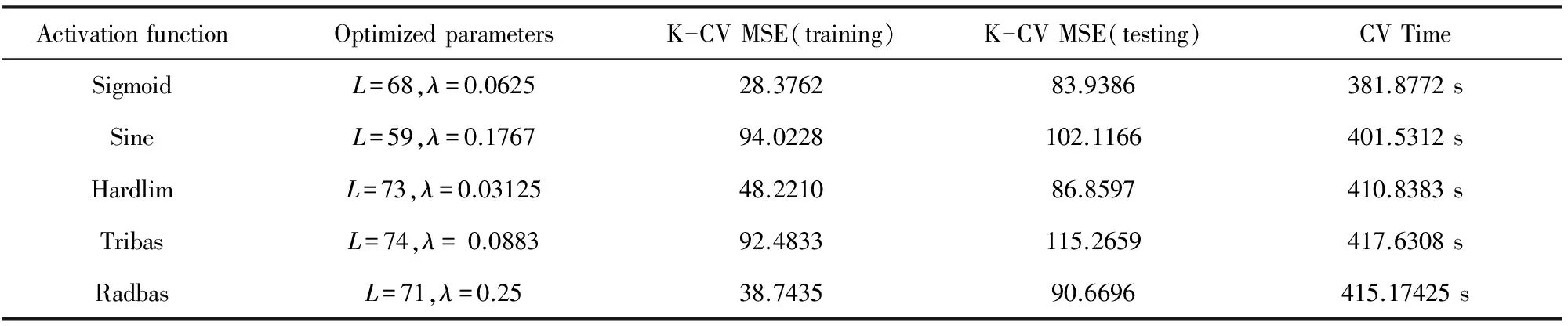
表1 不同参数下ELM反演的性能比较Table 1 Comparison on performance of ELM inversion using different parameters

图6 基于PC-RELM的超高密度电法反演流程图Fig.6 Flowchart for ultra-high density resistivity method inversion based on PC-RELM

(4)根据超高密度电法的采集数据规划训练和测试样本；

(5)对样本中的高维特征数据进行PCA降维，选择满足阈值设定的主成分构成新的训练和测试样本；

(6)输入训练数据集，在当前的训练与测试环境下，通过K-CV方法对ELM的参数进行优选，其主要包括激活函数类型的选择，L和λ参数的寻优；

(7)对参数寻优后的ELM进行训练，并保存训练后的ELM；

(8)输入测试数据集，使用构造好的ELM进行反演，输出并评估反演结果.

上述步骤对应的反演流程如图 6所示.

5 模型反演

为了验证本文所提出的PC-RELM方法的反演性能，本文对两个经典的超高密度电法理论模型进行了反演研究，并比较与分析了本文方法与其他经典反演方法的反演结果.

模型1主要用来检验超高密度电法在垂直方向上对深部异常体的分辨能力，由四个不同深度的高阻异常体构成(Loke et al., 2010; Wilkinson et al., 2006)，引入该模型来验证超高密度电法分辨深部异常的能力.本文通过将超高密度电法的泛装置与Wenner，Wenner-Schlumberger和Dipole-Dipole三种四极装置的反演结果进行比较，验证本文所提出的超高密度成像非线性反演算法的性能.四种装置的参数设置和反演误差如表2所示.超高密度电法装置采用本文的反演方法，其他三种四极装置采用最小二乘法(RES2DINV软件)进行反演.四种装置的反演结果如图7所示.

由图7可知，传统的Wenner，Wenner-Schlumberger和Dipole-Dipole三种装置均能够较好地反演出浅层的三个高阻异常体的位置和形态，但对于5 m以下的高阻异常体，三种装置均无法获得满意的反演结果，而基于PC-RELM方法的超高密度电法反演由于采集的数据量大、信息丰富，为深部异常体的反演提供了更多的依据，能够较好地反演出5 m以下的高阻异常体的位置及形态，其反演结果优于三种传统装置的最小二乘反演.

模型2主要用来检验超高密度电法在高对比度模型下对低对比度异常体的分辨能力，它包含了一个高阻异常体、一个低阻层状介质和一个组合低阻异常体.对该模型进行深入研究表明，传统的Wenner和Dipole-Dipole装置均无法反演出模型2的组合低阻异常体，而基于多电极装置的超高密度电法反演则能够获得较好的反演结果(Stummer et al., 2004; Wilkinson et al., 2006; Zhe et al., 2007).本文在上述研究的基础之上，构建了4种超高密度电法的非线性反演模型，以验证非线性反演方法在超高密度反演中的性能.四种非线性反演方法中，BPNN为BP神经网络方法，已广泛地应用于电阻率成像反演；GRNN为广义回归神经网络，是RBF神经网络的一种改进，在一维电测深中已有初步的应用(Srinivas et al, 2012)；ELM为标准的极限学习机模型，PC-RELM为本文根据超高密度电法反演所提出的主成分正则化极限学习机模型，四种非线性反演方法的参数设置如表3所示.

图7 模型1的模型示意图及不同装置的反演结果(a)模型1示意图；(b)Wenner装置；(c)Wenner-Schlumberger装置；(d) Dipole-Dipole装置；(e)超高密度电法装置.Fig.7 Model one and inversion results by different configurations(a) Model 1; (b) Wenner configuration; (c) Wenner-Schlumberger configuration; (d) Dipole-Dipole configuration; (e) Ultra-high density resistivity method configuration.

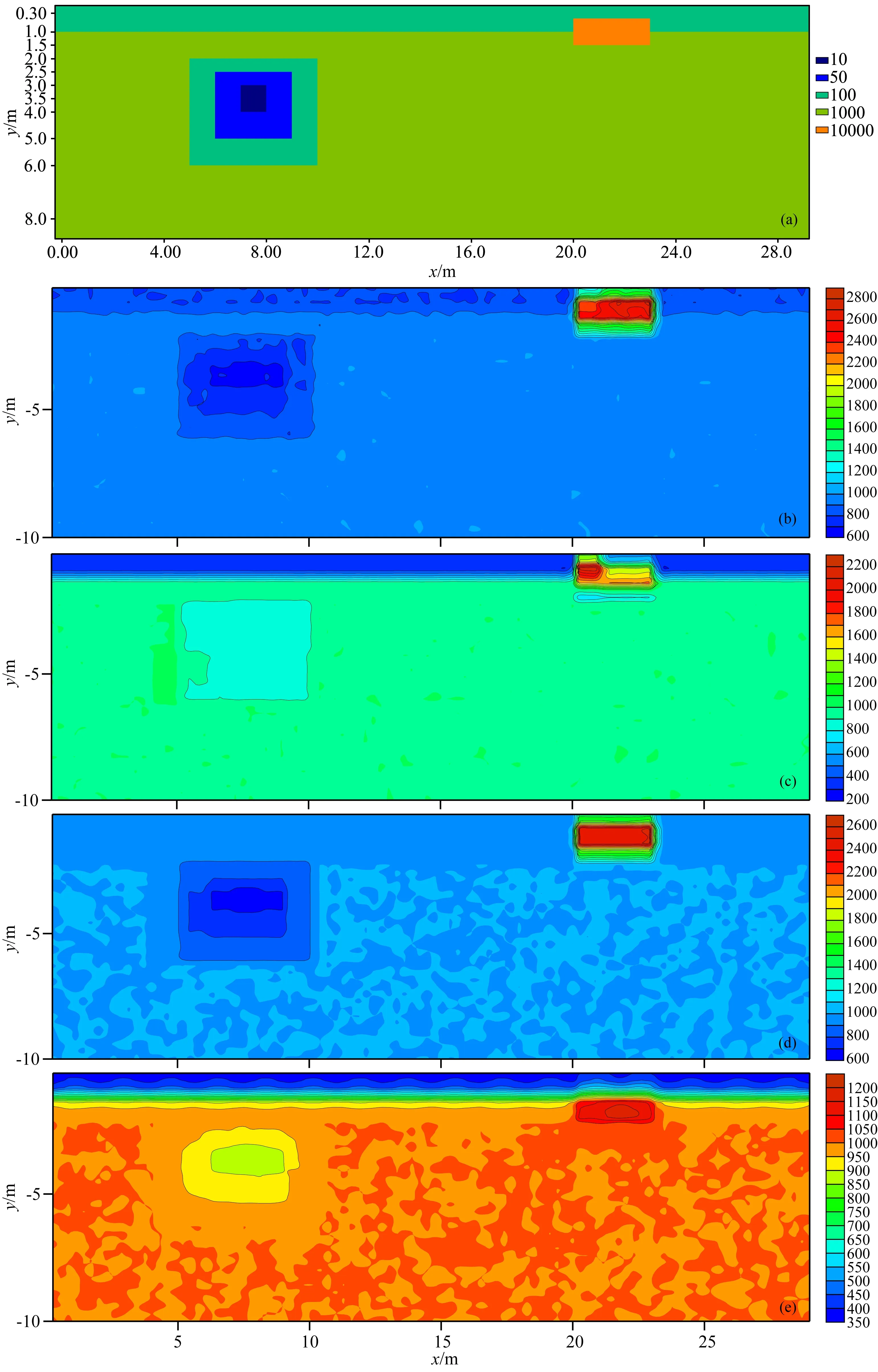
图8 模型2的模型示意图及不同非线性方法的反演结果(a)模型2示意图；(b)PC-RELM；(c)ELM；(d) BPNN；(e)GRNN.Fig.8 Model two and inversion results by different nonlinear inversion methods(a) Model 2; (b) PC-RELM； (c) ELM； (d) BPNN； (e) GRNN.

表2 不同装置反演结果比较Table 2 Comparison of inversion results form different configurations

表3 不同非线性反演方法的参数设置Table 3 Parameters for different nonlinear inversion methods

由图 8可知，四种非线性反演方法均能够在不同程度上反演出组合低阻异常体，相对而言，PC-RELM 和BPNN反演得到的组合低阻异常体其形态更加准确，但是BPNN对低阻层状介质的反演结果不佳，这是因为BPNN的全局响应特性使得低阻层状介质的反演结果受高阻异常体的影响较大而造成的；GRNN也能够获得模型中的各个异常体，但由于网络收敛于样本量聚集较多的优化回归面，因此其反演结果中高低阻异常体的阻值较为接近，与实际模型存在较大误差；标准的ELM因为未考虑正则化因子，受噪声的影响，ELM的反演结果在高低阻异常体的形态上存在一定的失真.本文所提出的PC-RELM算法则能够较好地反演模型中的各个异常体，在形态和电阻率值上均与理论模型更为接近.

表4进一步给出了四种非线性反演方法在训练和测试阶段的均方误差MSE和决定系数R2以及PCA降维(阈值设定为99%)前后的计算时间.其中均方误差MSE代表预测误差，其值越小，表示反演模型的预测误差越小；决定系数R2代表预测值与测量值之间的相关度，其值越大，表示两种数据间存在着越明显的线性相关性；计算时间的运行环境如下：CPU为Core(TM)i5-2450，内存为2GB，操作系统Windows XP SP4.通过PCA降维后的样本因为压缩了输入维度，降低了神经网络模型的复杂度，因此四种非线性反演方法的计算时间均少于降维前的计算时间，同时由于RELM、ELM都是随机获取隐层参数并通过求解Moore-Penrose广义逆矩阵得到输出参数，其计算时间均优于需要计算隐层参数的GRNN和基于迭代的BPNN算法.在训练阶段，由于ELM算法是通过求解广义逆矩阵直接拟合训练样本，因此训练误差最小；RELM虽然引入了正则化因子，但基于和标准的ELM算法同样的训练方式，训练误差也相对较小；BPNN和GRNN的训练误差则相对较大；在测试阶段，RELM表现出较高的泛化性能，得到了最小的训练误差，BPNN由于其全局响应的能力，将误差的影响均分至了各个网络节点，也获得了较小的训练误差，而标准的ELM和GRNN的测试误差则相对较大.以上结论也可以从R2指标中得到进一步验证.

表4 不同非线性反演方法的性能比较Table 4 Comparisons on performance using different nonlinear inversion methods

6 结论

超高密度电法一方面为地质资料的解释提供了更为丰富的高维数据，高维数据中所蕴含的电位差信息能够为高精度的电阻率成像提供信息基础；另一方面维数的增长又带来了“维数灾难”问题，为通过高维数据学习和建立非线性反演模型带来极大的挑战.本文根据超高密度电法的特点，提出了一种基于主成分-正则化技术的ELM非线性快速反演方法，该方面采用ELM学习模型，其隐层参数随机获得，输出层参数通过求解Moore-Penrose广义逆矩阵获得，极大地简化了样本的学习过程；针对超高密度电法采集的高维样本数据，采用主成分分析法对输入样本进行降维，简化了样本的结构；加入了正则化因子，以克服样本中噪声对反演模型的影响，提高ELM学习模型的泛化能力；最后采用交叉验证的方法对建模中的三个核心参数：激活函数类型、隐节点数目和正则化因子进行了优选，得到了优化的PC-RELM非线性反演模型，给出了超高密度电法的正演方法和反演流程.通过两个经典的超高密度电法理论模型的反演结果可知，超高密度电法较传统的四极装置具有更高的分辨率，能够解决一些传统四极装置无法解决的特殊问题；非线性反演方法能够减少对初始模型的依赖，不易陷入局部极值，在超高密度电法反演中具有广泛的应用前景，但同时也需要解决高维样本数据所带来的计算效率问题；本文提出的PC-RELM非线性反演方法实现简单，计算效率高，泛化能力强，其反演结果优于最小二乘线性反演方法以及ELM、BPNN、GRNN等其他非线性反演方法.

Athanasiou E N, Tsourlos P I, Papazachos C B, et al. 2007. Combined weighted inversion of electrical resistivity data arising from different array types.JournalofAppliedGeophysics, 62(2): 124-140.

Feng D S, Wang P F, Yang B K. 2014. Finite element forward simulation and least square generalized inversion of ultra-high density resistivity method.TheChineseJournalofNonferrousMetals(in Chinese), 24(3): 793-800.

Fernández-Navarro F, Hervás-Martínez C, Sanchez-Monedero J, et al. 2011. MELM-GRBF: a modified version of the extreme learning machine for generalized radial basis function neural networks.Neurocomputing, 74(16): 2502-2510. Ghosh-Dastidar S, Adeli H, Dadmehr N. 2008. Principal component analysis-enhanced cosine radial basis function neural network for robust epilepsy and seizure detection.IEEETransactionsonBiomedicalEngineering, 55(2): 512-518.

Ho T L. 2009. 3-D inversion of borehole-to-surface electrical data using a back-propagation neural network.JournalofAppliedGeophysics, 68(4): 489-499.

Huang G B, Wang D H, Lan Y. 2011. Extreme learning machines: a survey.InternationalJournalofMachineLearningandCybernetics, 2(2): 107-122.

Huang G B, Zhu Q Y, Siew C K. 2006. Extreme learning machine: theory and applications.Neurocomputing, 70(1-3): 489-501.

Huang G B, Zhou H M, Ding X J, et al. 2012. Extreme learning machine for regression and multiclass classification.IEEETransactionsonSystems,Man,andCybernetics,PartB:Cybernetics, 42(2): 513-529.

Lei X Y, Li Z W, Zhe J P. 2009. Applications and research of the high resolution resistivity method in explovation of caves,minecned regions and Karst region.ProgressinGeophysics(in Chinese), 24(1): 340-347.

Liu B, Li S C, Nie L C, et al. 2012. 3D resistivity inversion using an improved Genetic Algorithm based on control method of mutation direction.JournalofAppliedGeophysics, 87: 1-8.

Loke M H, Wilkinson P B, Chambers J E. 2010. Fast computation of optimized electrode arrays for 2D resistivity surveys.Computers&Geosciences, 36(11): 1414-1426.

Luo J H, Vong C M, Wong P K. 2014. Sparse Bayesian extreme learning machine for multi-classification.IEEETransactionsonNeuralNetworksandLearningSystems, 25(4): 836-843.

Mohammed A A, Minhas R, Jonathan Wu Q M, et al. 2011. Human face recognition based on multidimensional PCA and extreme learning machine.PatternRecognition, 44(10-11): 2588-2597.

Neyamadpour A, Taib S, Wan Abdullah W A T. 2009. Using artificial neural networks to invert 2D DC resistivity imaging data for high resistivity contrast regions: A MATLAB application.Computers&Geosciences, 35(11): 2268-2274.Neyamadpour A, Wan Abdullah W A T, Taib S. 2010. Inversion of quasi-3D DC resistivity imaging data using artificial neural networks.JournalofEarthSystemScience, 119(1): 27-40.

Pidlisecky A, Knight R. 2008. FW2_5D: A MATLAB 2.5-D electrical resistivity modeling code.Computers&Geosciences, 34(12): 1645-1654.

Ravi V, Pramodh C. 2008. Threshold accepting trained principal

component neural network and feature subset selection: Application to bankruptcy prediction in banks.AppliedSoftComputing, 8(4): 1539-1548.

Reddy K N, Ravi V. 2013. Differential evolution trained kernel principal component WNN and kernel binary quantile regression: Application to banking.Knowledge-BasedSystems, 39: 45-56.Sharma S P. 2012. VFSARES—a very fast simulated annealing FORTRAN program for interpretation of 1-D DC resistivity sounding data from various electrode arrays.Computers&Geosciences, 42: 177-188.

Shaw R, Srivastava S. 2007. Particle swarm optimization: A new tool to invert geophysical data.Geophysics, 72(2): F75-F83.

Srinivas Y, Raj A S, Oliver D H, et al. 2012. A robust behavior of Feed Forward Back propagation algorithm of Artificial Neural Networks in the application of vertical electrical sounding data inversion.GeoscienceFrontiers, 3(5): 729-736.

Stummer P, Maurer H, Green A G. 2004. Experimental design: Electrical resistivity data sets that provide optimum subsurface information.Geophysics, 69(1): 120-139.

Sun Z L, Choi T M, Au K F, et al. 2008. Sales forecasting using extreme learning machine with applications in fashion retailing.DecisionSupportSystems, 46(1): 411-419.

Wilkinson P B, Meldrum P I, Chambers J E, et al. 2006. Improved strategies for the automatic selection of optimized sets of electrical resistivity tomography measurement configurations.GeophysicalJournalInternational, 167(3): 1119-1126.

Zhe J P, Greenhalgh S, Marescot L. 2007. Multichannel, full waveform and flexible electrode combination resistivity-imaging system.Geophysics, 72(2): F57-F64.

Zhong T. 2008. The applied research into the exploration of the gob by multi-channel, full waveform and flxible electrode combination resistivity imaging system [Ph.D.thesis] (in Chinese). Chengdu: Chengdu University of Technology.Zong W W, Huang G B. 2011. Face recognition based on extreme learning machine.Neurocomputing, 74(16): 2541-2551.

附中文参考文献

冯德山, 王鹏飞, 杨炳坤. 2014. 超高密度电法有限单元法正演与广义最小二乘反演. 中国有色金属学报, 24(3): 793-800.

雷旭友, 李正文, 折京平. 2009. 超高密度电阻率法在土洞、煤窑采空区和岩溶勘探中应用研究. 地球物理学进展, 24(1): 340-347.

钟韬. 2008. 超高密度电法在探测采空区中的应用研究[博士论文]. 成都: 成都理工大学.

(本文编辑 胡素芳)

Ultra-high density resistivity nonlinear inversion based on principal component-regularized ELM

JIANG Fei-Bo1,2， DAI Qian-Wei1*， DONG Li1,3

1SchoolofGeosciencesandInfo-Physics，CentralSouthUniversity，Changsha410083，China2CollegeofPhysicsandInformationScience,HunanNormalUniversity,Changsha410081,China3SchoolofInformationScienceandEngineering,HunanInternationalEconomicsUniversity,Changsha410205,China

Ultra-high density resistivity inversion is a complicated non-linear inversion problem, which is high dimensional and non-convex. The traditional approaches suffer from some common drawbacks: they are mostly linear approximations of nonlinear problems and critically depend on the initial models chosen for them. A principal component-regularized extreme learning machine (PC-RELM) nonlinear inversion method for high dimensional ultra-high density resistivity data is analyzed.An additional principal component analysis layer is used for dimensionality reduction of the data to increase the computational efficiency of ELM inversion. Then, random hidden layer parameters are used to simplify the learning process of ELM. Additionally, the regularization factor is introduced to improve the generalization ability of the inversion model.The experimental results demonstrate that the proposed method exhibits high inversion accuracy and can solve the ultra-high density resistivity inversion problem efficiently: (1) The effect of using PCA for reducing the dimensions of ultra-high density resistivity data is obvious, and variance contribution rate of the first principal component reaches up to 40% or more. The ultra-high density resistivity data are reduced to 19 dimensions through the PCA layer with little information loss. (2) Optimized number of hidden nodes and value of regularization factor are obtained by cross validation. ELM with Sigmoid kernel, which reaches the lowest training MSE 28.3762 and testing MSE 83.9386, is used for inversion modeling. (3) The proposed inversion method reconstructs the size, location and sharpness of the anomalous body better than Least-squares inversion results of Wenner, Wenner-Schlumberger and Dipole-Dipole configurations with the same electrode number. (4) The proposed inversion method is also compared with BPNN, RBFNN and GRNN for nonlinear inversion. The results show that the proposed method reaches the lowest testing MSE 128.1303, and achieves the highest testingR20.8508.In this study an implementation framework of PCA dimension compression and ELM modeling with regularization for ultra-high density resistivity inversion is proposed. PCA layer is used for dimension compression and principal component selection, and then an improved RELM with Sigmoid kernel is used for ultra-high density resistivity inversion. The proposed method is accurate, fast, and easy for implementation. Another advantage of our proposed method is the direct approach to the nonlinear task, which avoids linearization and the choice of appropriate starting models necessary for classical minimization methods. Despite this contribution, there are many remaining challenges for the future work. Firstly, the way to optimize the parameters of ELM with optimal structure could be studied more deeply including the examination of theoretical implications of the associated choices. Secondly, the extension of the method to more complex field data set could be of interest, both from theoretical and practical viewpoints. Finally, GPU parallel computation will be introduced to the proposed inversion method to improve calculation efficiency. Our future research will be directed toward the development of fast and effective inversion algorithm for large-scale ultra-high density resistivity data inference.

Ultra-high density resistivity method； Regularization； Extreme learning machine; Principal component analysis

10.6038/cjg20150928.

Jiang F B, Dai Q W, Dong L. 2015. Ultra-high density resistivity nonlinear inversion based on principal component-regularized ELM.ChineseJ.Geophys. (in Chinese),58(9):3356-3369,doi:10.6038/cjg20150928.

10.6038/cjg20150928

P631

2014-11-13，2015-07-03收修定稿

国家自然科学基金(41374118),教育部博士点基金(20120162110015)，湖南省教育厅科研优秀青年资助项目(15B138)，湖南省科技计划资助项目(2015JC3067)，中南大学博士后基金联合资助.

江沸菠，男，1982年生，博士，讲师，主要从事电磁法非线性反演，人工智能工程应用等方向的研究.E-mail:jiangfeibo@126.com

*通讯作者 戴前伟，男，1968年生，博士，教授，1997年毕业于中南工业大学资源环境与建筑工程学院，主要从事电磁法方法及理论、工程地球物理勘探等方向的研究.E-mail: qwdai@csu.edu.cn

江沸菠, 戴前伟,董莉等. 2015. 基于主成分-正则化极限学习机的超高密度电法非线性反演.地球物理学报，58(9):3356-3369,