土壤非饱和区含水层对潮致地下水波动的影响

程博超，罗照阳，严佳伟，孔 俊，2

(1.河海大学港口海岸与近海工程学院，江苏南京 210098;

2.河海大学水文水资源及水利工程科学国家重点实验室，江苏南京 210098)

目前，沿海地下水运动问题研究已成为国内外的热点课题之一［1-2］。传统Boussinesq方程的理论研究［3-5］均假定地下水自由面是饱和含水层和不含水层间的突变界面，实际上这一突变界面并不存在，而是存在一过渡区(又称毛细效应区)［6］。Millham等［7］曾经指出，如果不考虑非饱和流的存在，会严重错估地下水头的时空特征。为了进一步分析2种不同区域的相互影响，Parlange等［8］引入Green等的假定，在方程中添加了高阶项，提出考虑毛细效应的Boussinesq方程。Barry等［9］研究表明，在一般情况下对于长周期波(如潮波)，紧邻饱和区上层的毛细效应作用不明显，但对高频波(波浪)来说，毛细效应的诱发作用较明显，在非饱和区作用下高频波向潜水层传播时，向陆一侧衰减速度会有所减慢，位相偏移减小，传播距离更远。Li等［10-11］通过对高频波动的数值模拟证实了这一现象的存在并将修正项引入中等水深Boussinesq方程，扩展了其在描述高频波传播方面的适用范围。但上述研究考虑的毛细效应区仅仅是位于非饱和区与饱和区交界处较窄的一段饱和负压区，不能完全代表非饱和区的效用。为此，Kong等［12］针对上述不足，提出了一个在有限非饱和厚度区域内、综合考虑水平和垂向流的新型地下水波动控制方程。本文针对该方程通过摄动解析法剖析波动组成和波动的函数表达，进一步分析波动特征并对其影响因素展开分析。

1 控制方程

Kong等［12］基于Richards方程［13］，通过静压法和动压校正法推求的地下水Boussinesq方程可表述为

其中

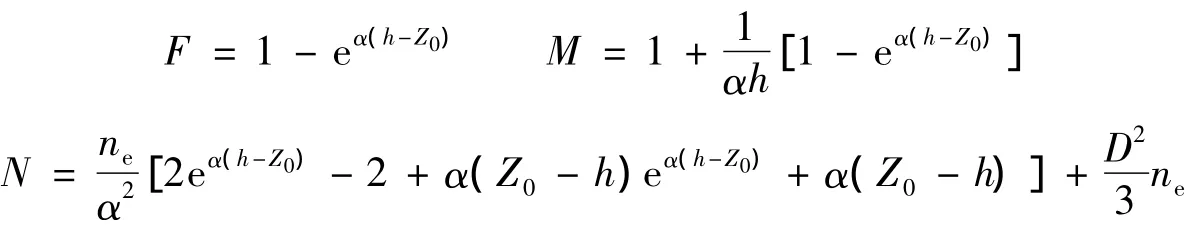
边界条件为

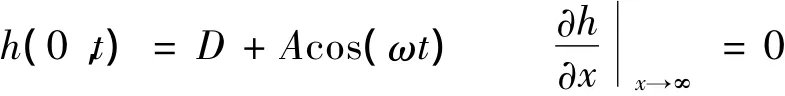
式中:ne——土壤的有效孔隙率;h——地下水水头高度;Ks——土壤的渗透系数;α——与土壤非饱和特性成反比的参数，反映土壤的含水特性;Z0——土壤层顶面高度;D——平均海平面以下的潜水层厚度;A——地下水波动振幅;t——时间;ω——海潮波动频率。

2 解析解

针对上述方程，Kong等［12］通过小参数摄动法推求出方程的解析解，得到1阶主频波和2阶倍频波(弥散波)的解析表达形式，考虑到1阶主频波和2阶弥散波可基本反映潮波传入潜水层后的波动特征，本文重点分析这2个频率的波动特征和影响因素。1阶主频波表述为

2阶弥散波的解析表达式为

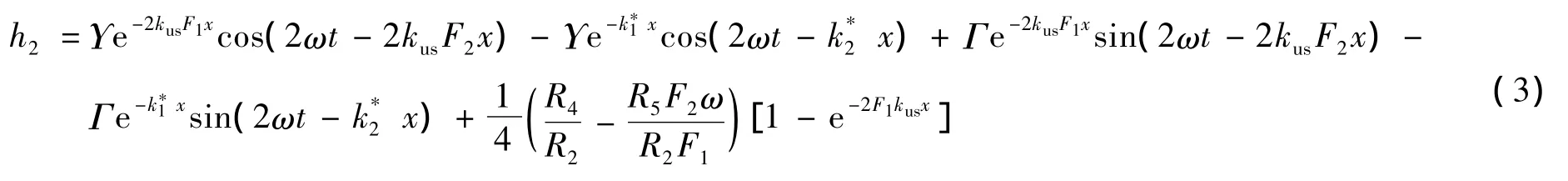
其中

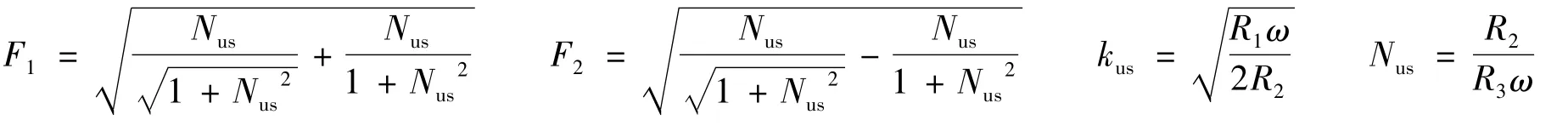
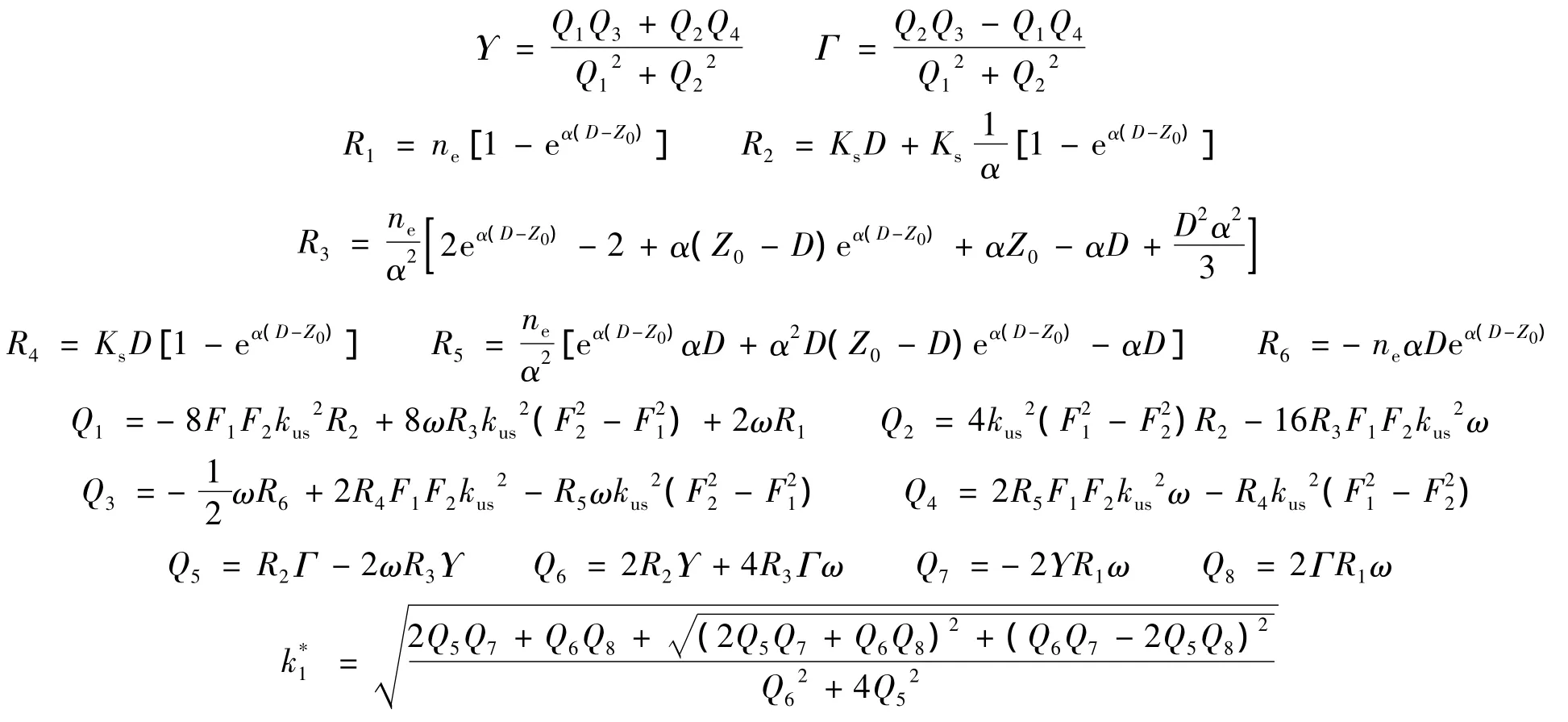
3 波动特征及影响因素分析

由于土壤的非饱和效应，潮波自外海传入潜水层后运动特征发生了明显的改变，在传播过程中，波的振幅出现了一定的衰减，同时产生了高频波。本文基于上述1阶主频波和2阶解析表达形式，分析各阶组成波振幅沿程变化特征及其主要影响因素。

分别将α、Z0、Ks、ne作为研究变量，并对1阶主频波、2阶弥散波波动方程(式(2)、式(3))中各常量参数赋值，得到5种取值方案，进而利用数值模拟方法绘出各取值情况下主频波与弥散波的波幅曲线，从而分析各参数变量对波幅的影响机制。以下是方案的取值情况。方案1:Z0=5.5 m，Ks=4×10-5m/s，T=12 h，D=5 m，ne=0.3，α 为变量;方案2:Ks=4 ×10-5m/s，T=12 h，D=5 m，ne=0.3，α =0.2，Z0为变量;方案 3:Ks=4 ×10-5m/s，T=12 h，D=10 m，ne=0.1，α =0.2，Z0为变量;方案4:Z0=5.5 m，Ks=4 ×10-5m/s，T=12 h，D=5 m，α =0.2，ne为变量;方案5:Z0=5.5 m，T=12 h，D=5 m，ne=0.3，α =0.2，Ks为变量。

3.1 α对波幅的影响

α是反映土壤非饱和持水特征的参数，其与土壤的非饱和程度成反比，其值越小，土壤的非饱和持水性越强。进一步结合已推求的解析解，对比不同α取值情况下各阶组成波振幅的沿程变化趋势，本文主要针对1阶主频波和2阶弥散波进行讨论。对于1阶主频波，沿程振幅呈指数型衰减。当α增大时，土壤的非饱和持水特性减弱，非饱和区持水能力降低，1阶主频波振幅的衰减速度加快，见图1(a)(其中A1、A2分别表示1阶主频波与2阶弥散波的波幅，下同)。对于2阶弥散波，沿程的振幅表现为先递增、后减小，反映了能量从低频波向高频波的迁移过程。当2阶弥散波从1阶主频波获得的能量大于其本身向3阶高频波的输出时，表现为其振幅不断增加;反之则表现为振幅不断减小。从图1(b)可以看出，当α取值越大时，2阶弥散波所能达到的最大振幅越临近海边界，同时振幅也越小。这是由于非饱和区持水能力降低后增加了波动传播的阻尼效应，限制了2阶弥散波的成长;当α减小时这种趋势恰好相反，2阶弥散波成长距离变长，最大波幅增大，表明土壤的非饱和效应有利于让能量更多地从低频波向高频波转移，使高频波的毛细效应更加显著。

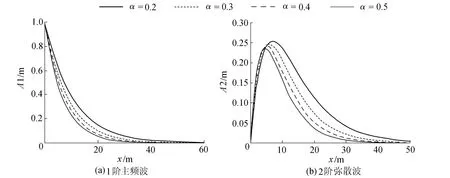
图1 α对波幅的影响(方案1)Fig.1 Impact ofα on amplitude in project 1

3.2 Z0对波幅的影响

Z0越大表明平均水面线高度以上的土壤层越厚。当保持外海潮汐振幅不变时，通过改变Z0，可分析不同非饱和区厚度影响下1阶主频波和2阶弥散波的振幅沿程变化趋势。从图2(a)、图3(a)可见，1阶主频波的振幅呈指数型衰减特征。当非饱和区厚度增大后，1阶主频波振幅沿程衰减速度变快。分析其原因在于随着潜水面上层土壤层厚度的增大，非饱和区持水量也逐渐增大，上层非饱和区与下层饱和区之间垂向水量交换作用加强，由于土壤含水量与气压之间的关系，增厚的非饱和区需要获取更多的水分得以维持，这就迫使1阶主频波在传播过程中不仅需要在水平方向输送水分，同时在垂向上还要不断补给非饱和区，因而就促进了1阶主频波的能量衰减。此外从图2(b)、图3(b)可以看出，非饱和区厚度增大后，2阶弥散波的成长受限，其所能达到的最大振幅也有所减小。这表明，在保持土壤持水特性不变的情况下，非饱和区厚度加大后，由于1阶主频波波能衰减速度加快，部分能量用于维持非饱和区内水体的运动，限制了其本身能量向高频波的迁移，导致高频波的振幅呈现出减弱的趋势。

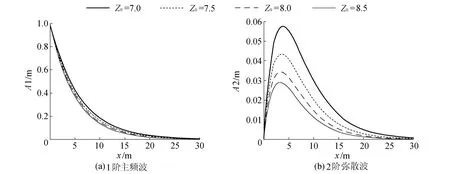
图2 Z0对波幅的影响(方案2)Fig.2 Impact of Z0 on amplitude in project 2

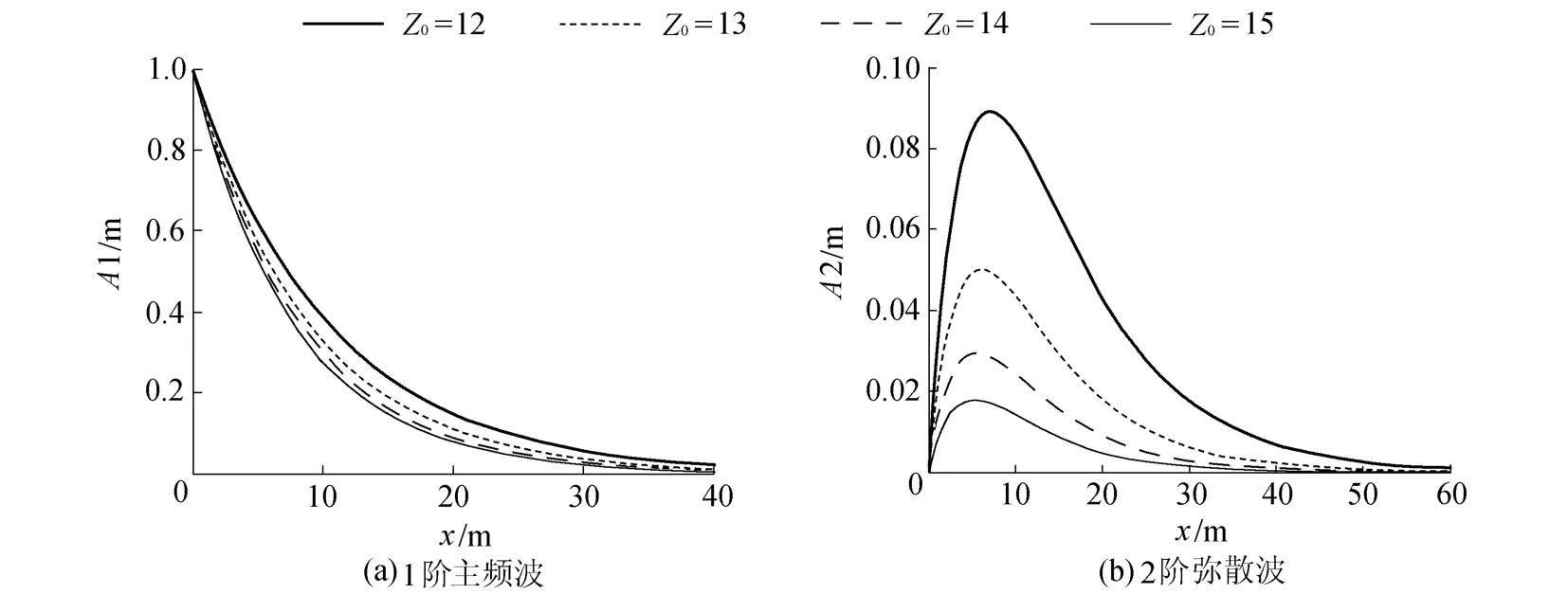
图3 Z0对波幅的影响(方案3)Fig.3 Impact of Z0 on amplitude in project 3

3.3 n e对波幅的影响

从图4可见，考虑非饱和区存在时，随着ne增大，1阶主频波的振幅衰减速度增快，1阶主频波能量转移到2阶弥散波的速度加快，则2阶弥散波达到最大的成长距离变短，所能达到的最大振幅减小。

图4 参数n e对波幅的影响(方案4)Fig.4 Impact of n e on amplitude in project 4

3.4 Ks对波幅的影响

Ks越大，土壤的渗透性越强。从图5可见，当考虑土壤非饱和效应时，随着Ks增大，1阶主频波的振幅沿程衰减速率减慢。对于2阶弥散波，随着Ks增大，能量从1阶主频波转移到2阶弥散波的速度减慢，2阶弥散波所能达到的最大振幅也变大。

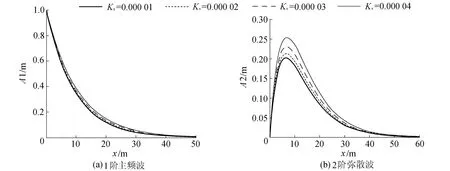
图5 参数Ks对波幅的影响(方案5)Fig.5 Impact of Ks on amplitude in project 5

4 结 论

a.潜水层内1阶主频波的振幅沿程呈指数形式衰减;2阶弥散波的振幅沿程变化特征为先增大、后减小，体现出能量从低频波向高频波迁移的过程。

b.各因素对比表明，非饱和区土壤持水能力越强，土壤渗透系数越大，越有利于高频波的产生和传播。

c.考虑到土壤层的非饱和持水效应，2阶弥散波所能达到的最大振幅比不考虑土壤非饱和效应时大，说明考虑土壤非饱和效应时2阶弥散波所获得的能量较多。因此土壤的非饱和效应对于诱发非饱和区含水层内的高频波起到促进作用，而传统的地下水波动方程忽略了这一物理现象，导致对高阶倍频波的形成认识存在不足。

d.Kong等［12］提出的新型地下水Boussinesq方程中，关于土壤含水量和土壤渗透性的参数指标过于单一，为进一步深入剖析不同土壤环境下的地下水波动特征，还需要对上述控制方程做进一步完善，以期更深入地认识潜水层内的水波运动理论。

［1］陈吉余，陈沈良.中国河口海岸面临的挑战［J］.海洋地质动态，2002，18(1):1-5.(CHEN Jiyu，CHEN Shenliang.Estuarine and coastal challenges in China［J］.Marine Geology Letters，2002，18(1):1-5.(in Chinese))

［2］HORN D P.Beach groundwater dynamics［J］.Geomorphology，2002，48:121-146.

［3］NIELSEN P.Tidal dynamics of the water table in beaches［J］.Water Resource Research，1990，26(9):2127-2134.

［4］LI Ling，BARRY D A，PATTIARATCHI C B.Numerical modeling of tide-induced beach water table fluctuations［J］.Coastal Engineering，1997，30:105-123.

［5］PARLANGE JY，STAGNITTI F，STARR J L，et al.Free-surface flow in porous media and periodic solution of the shallow-flow approximation［J］.Journal of Hydrology，1984，70:251-263.

［6］TURNER I.Water table outcropping on macro-tidal beaches:a simulation model［J］.Marine Geology，1993，115:227-238.

［7］MILLHAM N P，HOWESB L.A comparison of methods to determineKin a shallow coastal aquifer［J］.Ground Water，1995，33(1):49-57.

［8］PARLANGE J Y，BRUTSAERT W.A capillary correction for free surface flow of groundwater［J］.Water Resource Research，1987，23:805-808.

［9］BARRY D A，BARRY SJ，PARLANGE J Y.Capillarity correction to periodic solutions of the shallow flow approximation［M］.Washington，D.C.:American Geophysical Union，1996:496-510.

［10］LI Ling，BARRY D A，PATTIARATCHI C B.Numerical modeling of tide-induced beach water table fluctuations［J］.Coastal Engineering，1997，30:105-123.

［11］LILing，BARRY D A，CUNNINGHAM C，et al.A two-dimensional analytical solution of ground-water responses to tidal loading in an estuary and ocean［J］.Advance of Water Resource，2000，23:825-833.

［12］ KONG Jun，SHEN Chengji，XIN Pei，et al.Capillary effect on water table fluctuations in unconfined aquifers［J］.Water Resource Research，2013，49:1-6

［13］GARDNER W R.Some steady-state solutions of the unsaturated moisture flow equations with application to evaporation from a water table［J］.Soil Science，1958，85(4):228-232.