下凹型内孤立波沿台阶地形演化特征试验

屈子云，魏 岗，杜 辉，靖树一，王欣隆

(解放军理工大学气象海洋学院，江苏南京 211101)

海洋内孤立波是发生在密度稳定层化的海水内部的一种特殊波动，我国南海海域是内孤立波的多发地，内孤立波在吕宋海峡以及吕宋海峡西北方向大陆架区域的动力学特征一直是中外学者十分关注的问题［1-3］。内孤立波在向浅海区域传播的过程中会与海底变化的地形发生相互作用，其过程常伴有反射、透射、分裂以及极性转换(即下凹型转化为上凸型)等非线性演化特征［4-5］。南海北部海域地形复杂、流态格局多变、密度垂向层化特征显著，为内孤立波的产生提供了条件，尤其是东北部海域大振幅内孤立波频发并沿着陆架陆坡地形向东沙群岛方向传播，内孤立波与海底地形相互作用的现象时有发生。另外由于温度、洋流等影响，海洋跃层与海底地形的相对位置也会发生变化，同样会对内孤立波与海底地形的相互作用产生影响。

针对内孤立波与地形的相互作用，很多学者用不同的方法进行了研究。魏岗等［6］基于边缘层理论研究了两层流体中内孤立波在台阶地形上透射、反射及其分裂的演化特征;Xu等［7］通过理论模型和试验研究相互验证，证明了KdV方程在研究内孤立波沿地形传播时的适用性;另外，用数值模拟结合实测资料以及卫星图片的方法也被广泛采用［8-10］。由于内孤立波与地形相互作用的复杂性，理论研究和数值模拟对作用过程中的细节无法准确测量，试验研究仍是目前研究大振幅内波变形、破碎、混合等复杂过程的有效方法。自20世纪80年代以来，在分层流水槽中研究内孤立波与地形相互作用一直是认识海洋内孤立波沿海底地形传播的重要手段。贾村［11］研究了上凸型内孤立波在两层流体中的分裂，证明了两层流体中内孤立子分裂理论的有效性;Chen等［12］研究了两层流体中内孤立波经陡坡时的能量耗散，讨论了各种因素对能量耗散的影响;Carr等［13］通过内孤立波在波浪地形上传播的试验和数值研究，阐述了内孤立波与地形作用产生混合及耗散的机理;Cheng等［14］完成了内孤立波在陡坡地形上传播的试验，探讨了下凹型内孤立波在突变地形上的极性转换以及影响内孤立波演化的因素;Ermanyuk等［15］进一步研究了水下圆柱与内孤立波相互作用问题。

目前，由于多数实验室所用的分层流水槽横截面面积狭窄，导致壁面效应显著，限制了人们对内孤立波沿地形演化的三维结构特征的认识。另一方面，内孤立波在台湾吕宋海峡产生后继续向西北方向的东沙群岛海域传播，该海域地形突变特征明显，其变化是近年来学者们关注的重点。鉴于上述，笔者从我国南海海底地形分布特点出发，将海洋内孤立波在水深急剧变化地形上的实际传播情形简化为其在台阶地形上的演化模型，借助大型分层流试验水槽，改变分层情况，采用染色标识和内波动态测量技术，对内孤立波与台阶地形的相互作用问题进行试验研究，以期深入了解分层效应对内孤立波沿海底地形传播特性和表观特征的影响。

1 试验装置和测量技术

试验在解放军理工大学大型重力式分层流试验水槽中进行。水槽主尺度为1 200 cm×120 cm×100 cm(长×宽×高)，采用“双桶”原理获取分层水环境。在水槽的两端分别安装内孤立波造波装置和内波消波装置。内波造波采用旋转百叶门重力式内孤立波造波装置［16］，该造波机利用重力塌陷式造波原理，可在任意跃层位置产生下凹型或上凸型内孤立波;内波消波采用三角楔形装置，可根据试验过程中分层流体界面位置与内孤立波振幅大小进行调节，用以获得最佳消波效果。

图1为试验装置示意图，取x轴正方向为水槽长度方向(水平向左)，z轴正方向为铅垂方向(垂直向上)，坐标原点O(0，0)位于水槽右端跃层位置。H为总深度，h1、ρ1和h2、ρ2分别为上下流体层的厚度和密度，h3为台阶顶部距跃层距离，λ、a和c分别为内孤立波波长、波幅和传播速度，η0和L0分别为重力塌陷式造波原理中的势阱深度和势阱宽度(势阱指塌陷式造波原理中初始扰动的矩形区域［16］)。台阶高度为h0=50 cm，由1块长400 cm、宽150 cm的水平板和1块高度为50 cm的竖直板(密度大于盐水)拼接组成。

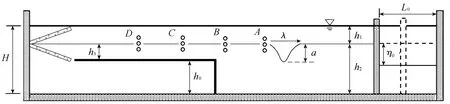
图1 试验装置示意图Fig.1 Schematic of experimental device

内孤立波与台阶相互作用的演化特征由染色界面的扰动显示，并由高分辨摄录系统记录。密度剖面和内孤立波要素的测量由多通道内波动态测量系统完成，通过记录若干垂向排列探头的时间序列密度值获得等密度面变化的空间分布，继而确定内孤立波的波高和波长;通过记录相邻两探头间的距离和扰动峰值之间的相关时间来确定内孤立波的传播速度。在图1中A(500，0)、B(590，0)、C(700，0)、D(800，0)处分别布置若干垂向分布的电导率探头阵列，可以获得不同位置处的内孤立波结构，从而分析得到其演化特征。

2 试验结果和分析

2.1 内孤立波演化特征

为模拟分层效应的影响，将分层流体上下层厚度比例分为3种情况进行试验，即h1/h2=10/70，20/60和15/65，则台阶地形相对跃层位置对应有3种情况，即h1＜h3，h1＞h3和h1=h3。根据两层流体理论，当上层流体厚度小于下层流体厚度时，所形成的稳定孤立波为凹型波;反之，内孤立波为凸型波。对于h1/h2=10/70，在台阶前后，上层流体厚度始终小于下层体流厚度，该种分层情况下凹型内孤立波始终是稳定的;对于h1/h2=20/60，在台阶前部表现为上层流体厚度小于下层流体厚度，在台阶上表现为上层流体厚度大于下层流体厚度，故该种分层情况可导致稳定的下凹型内孤立波向上凸型转化;对于h1/h2=15/65，在台阶前部，上层流体厚度小于下层流体厚度，而在台阶上，上下两层流体厚度相同，该种分层情况对应临界分层状态［6］。

2.1.1h1/h2=10/70

取不同的势阱深度，观察不同波幅的内孤立波与台阶地形相互作用的情况，以典型的势阱深度η0=15 cm为例，当h1/h2=10/70时，在试验观测中，下凹型内孤立波与台阶地形无直接作用，受地形的实际影响较小，波形保持良好，未发生极性转换现象。

由电导率探头阵列数据可进一步分析内孤立波与台阶地形相互作用的定量信息。图2是相同势阱深度条件下不同位置探头测得的波形。从不同位置(A、B、C、D)的探头阵列实测波形可以更清楚地看到:初始内孤立波保持较好的对称性(图2(a));当内孤立波传播至台阶附近，其前部与台阶接触，波形逐渐变陡，波幅逐渐增加(图2(b));内孤立波继续传播至台阶上，其波形依然保持较好(图2(c))，但随着传播距离增加，内孤立波开始逐渐消散，波幅明显减小(图2(d))。

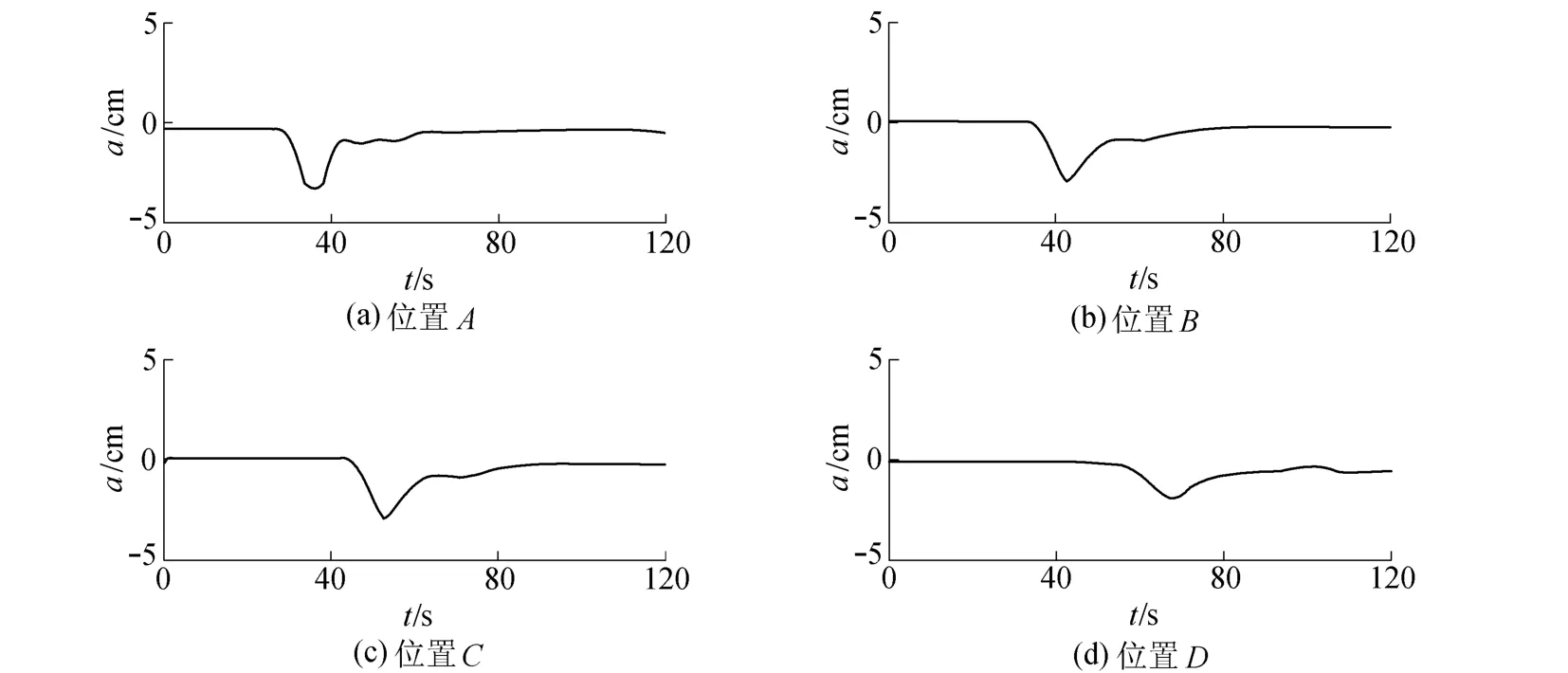
图2 h1/h2=10/70时内孤立波在4种不同位置的波形Fig.2 Profiles of ISW at four positions when h1/h2=10/70

2.1.2h1/h2=20/60

图3为h1/h2=20/60时内孤立波沿台阶地形演化的过程。试验结果表明:当内孤立波前部刚与台阶接触时，出现明显的水流从台阶上向下流动(图3(a));当内孤立波波谷抵达台阶时，波谷下方出现明显的涡旋(图3(b));当内孤立波传上台阶时，发生明显的极性转换，即内孤立波由凹型波转变为凸型波(图3(c)(d))。

从探头阵列实测波形可进一步看出:初始内孤立波保持较好的对称性(图4(a));在内孤立波即将接触到台阶地形时，波形变尖，波幅增大(图4(b));当内孤立波刚接触到台阶地形时并没有立即发生极性转换，但其波形前部变缓、后部变陡;随着内孤立波沿台阶的继续传播，其发生极性转化，由凹型波变为凸型波(图4(d))。2.1.3h1/h2=15/65

图3 下凹型内孤立波沿台阶地形传播的试验图片Fig.3 Interaction of ISW of depression and step topography

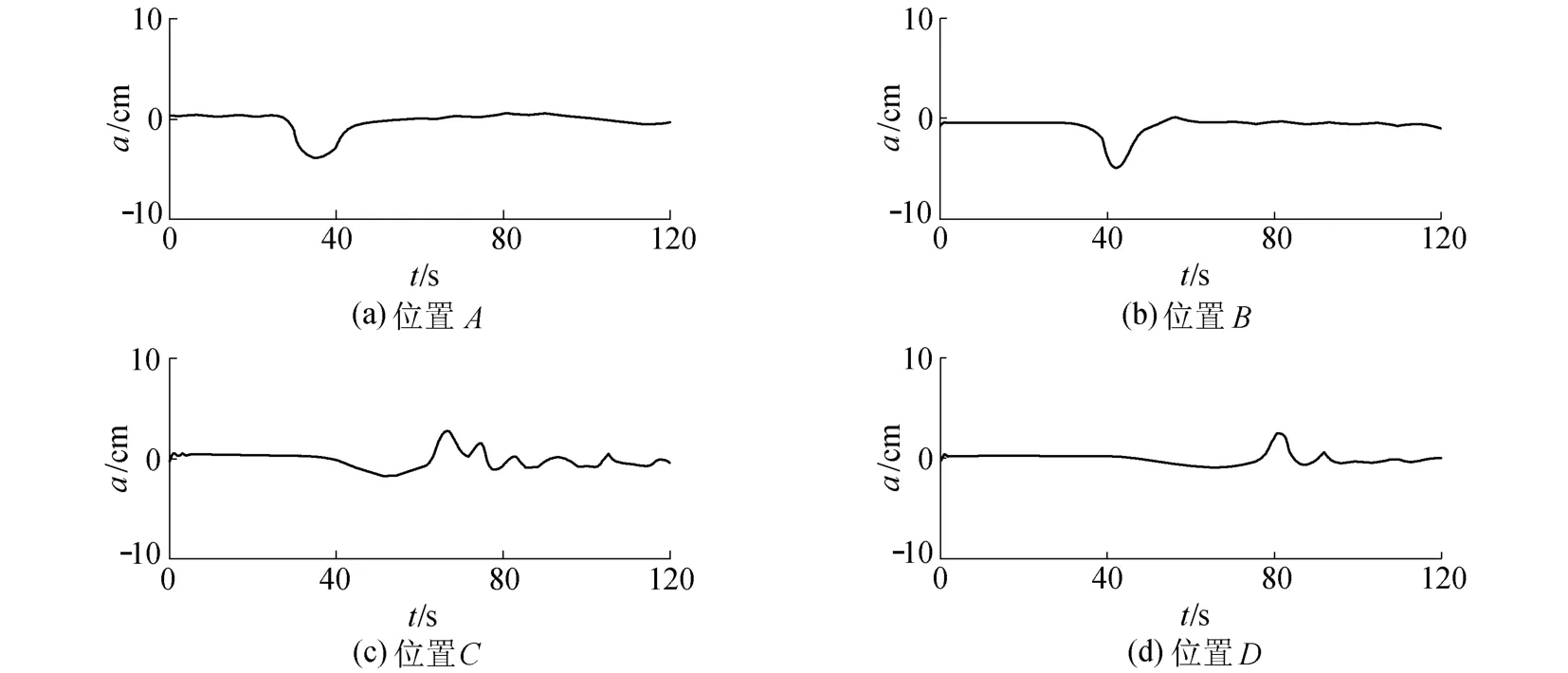
图4 h1/h2=20/60时内孤立波在4种不同位置的波形Fig.4 Profiles of ISW at four positions when h1/h2=20/60

试验观测发现:当内孤立波传播至台阶附近时，波谷与台阶相互作用，在其下方产生了一个顺时针方向旋转的涡旋，类似于图3(b)的情形;当内孤立波传播至台阶上时，涡旋在原处发展并逐渐扩散，使波的背部抬升;在整个传播过程中，并未发生极性转换现象。从探头阵列实测波形可进一步看出，内孤立波经过台阶地形时会出现频率较高的振动，即产生尾部波列效应(图5(b)(c))，界面处于不稳定状态，能量耗散明显，波幅衰减更快(图5(d))。

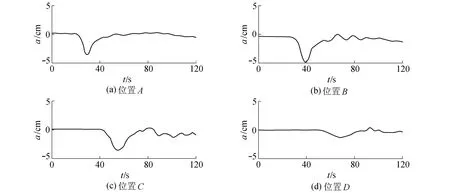
图5 h1/h2=15/65时内孤立波在4种不同位置的波形Fig.5 Profiles of ISW at four positions when h1/h2=15/65

2.2 内孤立波波幅变化特征

图6为3种不同分层情况下内孤立波与台阶地形作用前后的波幅变化情况。

图6 内孤立波传播过程中的波幅变化Fig.6 Amplitude variations of ISW in propagating process

a.对于h1/h2=10/70的情况，在内孤立波遇到台阶之前，由于台阶对内孤立波的“遮拦效应”，出现了波幅增大的现象，但随着内孤立波在台阶上的传播，能量耗散作用使波幅减小，在590 cm≤x＜800cm范围基本呈逐渐减小的趋势，但波幅仍然可以保持初始入射波波幅的水平，在x≈800 cm处的波幅与x≈500 cm处初始入射波幅基本一致。

b.当h1/h2=20/60时，在内孤立波遇到台阶之前依然出现波幅增大现象，在500cm＜x＜590cm范围波幅明显增大;随着极性转化的发生，波幅明显减小，台阶上传播至位置x≈700 cm处的内孤立波波幅明显小于入射波波幅;由于浅水效应，在700 cm＜x＜800 cm范围，台阶上转化为凸型波的内孤立波波幅继续增加。

c.对于h1/h2=15/65的情况，在500 cm＜x＜590 cm范围内孤立波波幅明显增大，随着内孤立波在台阶上的传播，由于能量耗散较快，在590 cm≤x＜800 cm范围波幅衰减较快。

3 结 论

a.内孤立波与台阶地形作用过程中，台阶作用可导致内孤立波发生波形变陡、尾部波列和极性转换现象。当台阶上的上下两层流体厚度相等时(h1=h3)，内孤立波在台阶上传播最不稳定，能量耗散效应更明显。

b.内孤立波与台阶地形作用过程中波幅变化较大，尤其内孤立波与台阶地形相遇的初始阶段，波幅增加最明显，验证了实际海洋中突变地形会导致内孤立波能量聚集的观测结论。

c.通过考察分层流体中不同上下层厚度比h1/h2下的内孤立波沿台阶地形传播的演化特征，证明了分层效应对内孤立波沿台阶地形传播的影响，获得不同分层环境下内孤立波的传播规律。

［1］CHEN Chenyuan.An experimental study of stratified mixing caused by internal solitary waves in a two-layered fluid system over variable seabed topography［J］.Ocean Engineering，2007，34:1995-2008.

［2］赵国君，邵利民，陈旭.内孤立波过山脊地形演化实验研究［J］.海洋工程，2013，31(4):42-47.(ZHAO Guojun，SHAO Linmin，CHEN Xu.An elementary research on the evolution of internal solitary wave crossing ridge topography［J］.The Ocean Engineering，2013，31(4):42-47.(in Chinese))

［3］MADERICH V，TALIPOVA T，GRIMSHAWR，et al.Interaction of a large amplitude interfacial solitary wave of depression with a bottom step［J］.Physics of Fluids，2010，22(7):0766021-07660212.

［4］BAINESP G.Topographic effects in stratifies flows［M］.Cambridge:Cambridge University Press，1995:325-329.

［5］CHENG Minghung，HSU JR，CHEN Chenyuan.Modelling the propagation of an internal solitary wave across double ridges and a shelf-slope［J］.Environ Fluid Mech，2009，9:321-340.

［6］魏岗，尤云祥，缪国平，等.分层流体中内孤立波在台阶上的反射和透射［J］.力学学报，2007，39(1):45-53.(WEI Gang，YOU Yunxiang，MIAO Guoping，et al.Reflection and transmission of an internal solitary wave over a step in stratified fluid［J］.Chinese Journal of Theoretical and Applied Mechanics，2007，39(1):45-53.(in Chinese))

［7］XU Zhaoting，XU Hao，SHEN Guojin.Evolution of interface soliton over topography［J］.China Ocean Engineering，2007，21(1):39-49.

［8］沈国瑾.陆架陆坡区初始内孤立波分裂的研究［D］.青岛:中国海洋大学，2004.

［9］孙丽，杜涛，李群.内孤立波的研究与数值模型［J］.海洋湖沼通报，2006(4):1-8.(SUN Li，DU Tao，LI Qun.A study of internal solitary waves and their numerical models［J］.Transactions of Oceanology and Limnology，2006(4):1-8.(in Chinese))

［10］孙丽.南海内孤立波的生成、演变及对桩柱的作用［D］.青岛:中国海洋大学，2006.

［11］贾村.孤立波在单层和两层流体中分裂的研究［D］.青岛:中国海洋大学，2006.

［12］CHEN Chenyuan，HSU JR，CHEN H H，et al.Laboratory observations on internal solitary wave evolution on step and inverse uniform slopes［J］.Ocean Engineering，2007，34:157-170.

［13］CARR M，STASTNA M，DAVIESPA.Internal solitary wave-induced flow over a corrugated bed［J］.Ocean Dynamics，2010，60:1007-1025.

［14］CHENG Minghung，HSU JR，CHEN Chenyuan.Laboratory experiments on waveform inversion of an internal solitary wave over a slope-shelf［J］.Environ Fluid Mech，2011，11:353-384.

［15］ERMANYUKE V，GAVRILOV N V.Experimental study of the dynamic effect of an internal solitary wave on a submerged circular cylinder［J］.Journal of Applied Mechanics and Technical Physics，2005，46(6):800-806.

［16］WEI Gang，DU Hui，QU Ziyun，et al.Experimental investigation of the generation of large-amplitude internal solitary wave and its interaction with a submerged slender body［J］.Science China:Physics，Mechanics＆ Astronom，2014，57(2):1-9.