测力平台系统输出压力中心参数的校正*

张文成,肖金壮,王洪瑞

(河北大学电子信息工程学院,河北 保定 071002)



测力平台系统输出压力中心参数的校正*

张文成,肖金壮*,王洪瑞

(河北大学电子信息工程学院,河北 保定 071002)

目前使用的应变式测力平台,其检测的压力中心都是以力平台初始标定数据作为依据。由于生产测力平台的工艺及技术问题,随着测力平台使用时间增加、工作环境变化,传感器参数随之改变,很大程度影响了测力平台测量精度。针对这种情况,本研究通过对测力平台静态标定,建立了输出特性校正模型,利用最小二乘法求解该模型参数,并应用软件补偿实现对测力平台的校正。基于实验结果,讨论了最优模型结构参数,表明了此方法能够补偿测力平台的非线性,可在一定的温度和压力内实现测量准确度优于1 mm,使测力平台满足人体COP测量评定要求。

测力平台;校正;压力中心;最小二乘法

压力中心COP(Center Of Pressure)是指人体向足底施加压力的合力作用点位置。已有研究表明,压力中心轨迹变化可直接反应脚踝肌肉的神经控制和施力模式。通过检测设备获取人体压力中心的变化,可以提供有关常态或病理状态下人体对姿势控制的相关信息,在评价人体站立平衡、步态分析中尤为重要[1-2]。生物力学研究对于压力中心测量的精度有着非常高的要求。例如,人体姿态描记时,测量仪器要求其精度优于0.1mm[3]。

然而在实际使用测力平台时,测量精度往往被忽视,影响人体研究的准确性。目前,国外对于应用测力平台检测压力中心的精确性的检验研究较多。如Harrison对Wii平衡板的测量准确度做了研究[4],Steven对测力平台进行线性校准[5]使其测量精度达到3mm。但是,通常采用的检测仪器较为复杂,一般条件较难实施,而且校正后的精度和稳定度也很难长时间保证。

基于以上考虑,本文研究得到了测力平台高精度、简易校正技术。通过对测力平台COP标定值的实验,建立了输出特性校正模型,并求解该模型最小二乘解中范数最小的唯一解[6]。然后运用软件编程,使测力平台每次开机时,系统根据输出校正模型对输出进行自动校正。实验结果表明,本设计改善了测力平台输出特性,且使用方法简便,可应用于实践。

1 研究对象与方法

1.1 力平台描述及COP算法

如图1所示,力平台包括两个圆形树脂刚性平台,直径为400 mm。在两个刚性平台之间有3个应变式拉压力传感器,且等边分布,构成边长为2a(a=115 mm)的等边三角形。每个传感器的输出电荷量与所受压力值成线性关系,经过16位A/D模块将电压值转化为数字量,滤波后通过串口传至PC/104[7]。然后力平台软件对这些值计算与分析得到压力中心[8-9]。

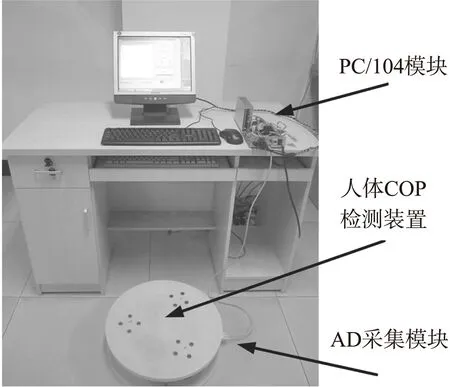
图1 测力平台系统构成

图2 测力平台系统原理图

由于力作用点P(px,py,pz)在测力平台表面,所以pz=0,只需求出力作用点在x轴坐标和y轴坐标。根据力矩守恒原理可得压力中心坐标P(px,py):

(1)

(2)

2 误差分析及校正方法

测力平台选用由恒流源供电的应变式传感器,它的工作参数,如温度、恒流源电流值等的波动,均会影响传感器的准确度,从而影响测力平台的精度,式(3)是在力传感器1产生ΔF误差时px的结果;测力平台在安装时,由于安装不够精密也会产生误差,比如力传感器安装位置的准确度,式(4)为在传感器安装时产生Δa误差时py的结果。

(3)

(4)

根据误差产生的原因,可以得出,测力平台的输出值与其标定值满足一定的非线性关系[10-11]。因此,为消除上述干扰因素的影响,可根据测力平台的静态特性标定试验数据集{pxi,pyi}拟合其输出特性[12]:

(5)

(6)上式中:px、py为测力平台待测压力中心标定位置坐标值,ox、oy为测力平台输出的测量值。在测量中,测力平台校正前的输出O(ox,oy),利用式(5)和式(6)可计算出消除各干扰项后的待测位置坐标,即测力平台校正后的输出值。首先对测力平台进行静态标定实验,将实验数据的标定值集{pxi,pyi}和其对应的测力平台输出值集{oxi,oyi}代入式(5)和式(6)中,得到其线性方程组,简洁表示成下列矩阵等式:

px=Oxa

(7)

py=Oyb

(8)

求解出两个方程组的未知量a=(a0,a1,…,am)T和b=(b0,b1,…,bn)T,可得校正后测力平台的压力中心COP值的输出特性。由于两式解法相同,这里仅对式(7),压力中心x轴方向上的坐标px进行分析。为求得方程(7)的数值解,本文采用最小二乘法,计算范数‖px-Oxa‖2值最小情况下的最优解。采用奇异值分解法解方程组,得最小二乘范数最小的唯一解[13],可得系数a构成的列向量a=(ATA)-1×ATpx[13-14]。则对任意待测压力中心COP,其校正后的输出值R(rx,ry)可以通过以下多项式求得:

(9)

(10)

式(9)和式(10)即为用标准压力中心拟合的输出。取m=0和n=0时,仅对测力平台的零点进行校正。当输出曲线为线性时,可取m=1,n=1,不仅校准零点而且也适当调整校正灵敏度。当输出曲线为非线性时,可适当选取n值,这样除了零点校正值a0和b0,灵敏度校正系数a1和b1外,还考虑了二次系数a2和b2,使其满足非线性补偿要求。

3 测力平台标定值和输出值的测量

本测量设计了自制加载装置如图3所示。它包括一个质量为5kg长为1.5m的钢杆,钢杆末端为钢珠。钢杆可以负载各种重量的哑铃。加载装置与力平台接触确保为垂直,减少相间干扰。此时加载重量的压力中心为钢杆与力平台接触的位置坐标。当钢杆与力平台接触面积越小时,压力中心的精确度越高。为此在钢杆的底端,即与测力平台平面接触面,采用钢珠接触,保证加载物品的压力中心的精度[15]。

力平台主要用于对人体COP的测量,而人的体重大多都在40kg～100kg之间,因此本研究主要围绕40kg～100kg的范围进行检测和校正。通过实验发现,对同一点用不同重量测量,其COP显示结果不大于0.01mm,说明重量的大小对测量的结果影响不大,这里选择了60kg重量对力平台进行检测和校正。通过试验发现,2cm左右间隔的测量点得到的校准结果最优。根据力平台工作面积,本校准过程均匀地选取40个点,测量其COP值。首先在测力平台表面准确安装好精度为0.1mm的坐标

纸,它可以准确标出测力平台的压力中心位置坐标。每次测量时,记录本次测量点在平面坐标纸上标定的位置坐标{pxi,pyi}及测力平台输出的相应位置坐标{oxi,oyi},得到实验数据集。

利用上文提到最小二乘拟合输出的方法,对实验数据集进行处理,即可得到校正模型。

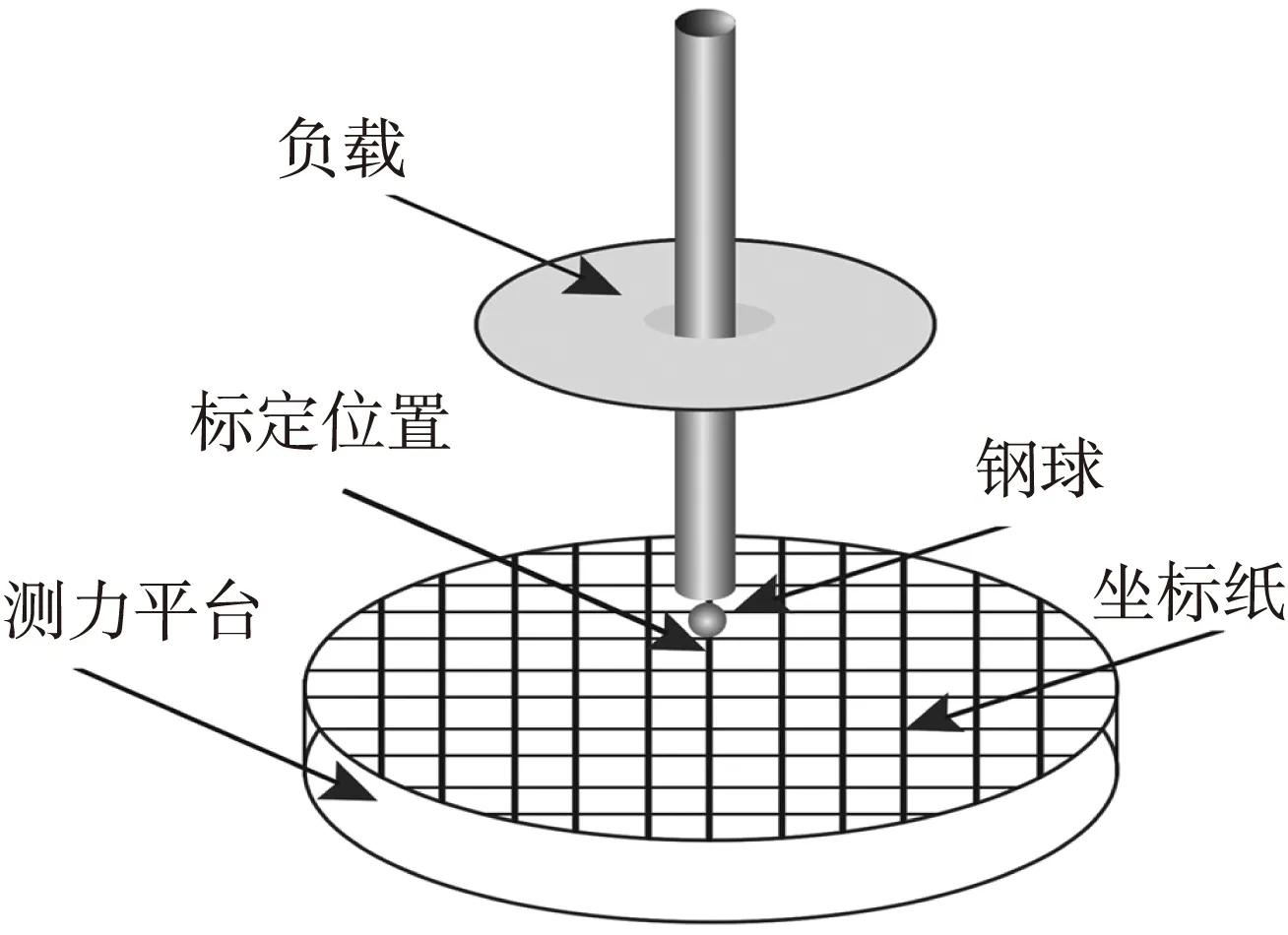
图3 加载装置示意图

4 结果与分析

根据所提出的校正方法和测量方法,对测力平台上已测几个位置坐标进行校正。当灵敏度m和n取不同值时,校正结果列于表1。可见,m和n的取值对校正结果影响明显,应选取适当。

表1 m,n不同值时校正结果

图4 m取值对压力中心x方向上校正的影响

如图4和图5所示,当m,n取不同值时,压力中心x轴和y轴方向上的最大绝对误差和均方根误差分布。当m=2时,压力中心x轴方向上校正效果最好,最大绝对误差降低了92%,由校正前的12.5mm减小到1mm;均方根误差降低了93%,由校正前的11.5mm减小到0.8mm。当n=2时压力中心y轴方向上校正效果最好,最大绝对误差降低了96%,由校正前的21.5mm减小到0.8mm;均方根误差降低了96%,由校正前的16.8mm减小到0.7mm。因此,当m=2、n=2时的校正模型最佳,对测力平台的校正精度最高。

图5 n取值对压力中心y方向上校正的影响

图6 压力中心输出值和标定值对比图

选取好最佳校正模型后,对测力平台进行了验证性检测。图6为测力平台坐标标定值和校准后的输出值对比效果图。可见,检测位置随机均匀地分布测力平台表面,且校准后的输出的位置坐标值与力平台坐标标定值误差均小于1mm,说明该校正模型有效地消除了测力平台的误差,显著提高了测量精度。

5 结论

本文对测力平台的压力中心进行标定实验,得到数据集,然后根据这些数据集建立压力中心的输出校正模型。利用最小二乘法求解该模型中的参数,并通过软件编程把最优校正模型写入测压力平台系统,使测力平台每次开机时,系统根据输出校正模型对输出进行自动校正。该校正方法有效地消除了测量误差,显著补偿了测力平台的非线性。

校正后的测力平台压力中心有很高的精确性,可为各群体人体站立平衡、步态分析提供检测依据,可进一步推广使用[3]。

本文提出的校正方法也可以应用到其他测力平台,进行周期性地评测和校正,确保测力平台测量的精度,以免测量的数据误差太大而影响压力中心检测结果。

[1] Cornwall M,Mcpoil T. Velocity of the Center of Pressure during Walking[J]. J Am Podiatr Med Assoc,2000,90(7):334-338.

[2] James B,Eric P. Center of Pressure of Trajectory Differences between Shod and Barefoot Running[J]. Gait and Posture,2014,40:504-509.

[3] Fabio S,Roberto C,Michele G. Clinical Stabilometry Standardization Basic Definitions-Acquisition Interval-Sampling Frequency[J]. Gait and Posture,2014,39:290-292.

[4] Harrison L,Lena H T,Jeffreey T B. Accuracy of Force and Center of Pressure Measures of the Wii Balane Board[J]. Gait and Posture,2014,39:224-228.

[5] Steven H C,Peter G A,Daniel P F. A Simple Method for Calibrating Force Plates and Force Treadmills Using an Instrumented Pole[J]. Gait and Posture,2009,29:59-64.

[6] 程秀芝,朱达荣,张申,等. 基于RSSI差分校正的最小二乘-拟牛顿定位算法[J]. 传感技术学报,2014,27(1):123-127.

[7] 肖金壮,睢少坤,王洪瑞. 基于随机视觉刺激的人体平衡能力评测系统研究[J]. 中国生物医学工程学报,2014,33(4):498-502.

[8] 殷代宗. 基于QNX实时操作系统的嵌入式测试系统的开发[D]. 西安:西北工业大学,2007.

[9] 张蓉,邓浩,王磊. 基于PC104的时序控制系统设计[J]. 计算机工程,2005,37(1):251-253.

[10] 刘渊. 误差理论与数据处理[D]. 辽宁:大连理工大学,2008.

[11] 范建英,李杰,陈文蓉,等. 高精度数字陀螺仪安装误差标定与补偿方法[J]. 传感技术学报,2013,26(4):525-529.

[12] 田垅,刘宗田. 最小二乘法分段直线拟合[J]. 计算机科学,2012,39(6):482-484.

[13] 贾小勇,徐传胜,白欣. 最小二乘法的创立及其思想[J]. 西北大学学报,2006,36(3):507-510.

[14] 鲁铁定,周世健. 总体最小二乘的迭代解法[J]. 武汉大学学报,2010,35(11):1351-1354.

[15] 孟昭莉,元文学,刘海斌. 压电式测力平台系统输出压力中心参数的实验研究[J]. 医疗卫生装备,2010,31(4):21-23.

张文成(1991-),男,河北大学电子信息工程学院硕士研究生,主要研究方向为信息处理与智能测控;

肖金壮(1976-),男,博士,河北大学副教授,硕士生导师,主要从事康复机器人方面的研究,robot@hbu.edu.cn。

A Method for Calibrating the Center of Pressure of Force Plate*

ZHANGWencheng,XIAOJinzhuang*,WANGHongrui

(College of Electric and Information Engineering,Hebei University,Baoding Hebei 071002,China)

In order to reduce the center of pressure(COP)errors from force plate,this paper proposes an effective method termed the Least-Squares calibration. In practical measurement,due to the properties of components of the sensor or the ambient environment,errors could occur,which make the force plate inaccuracy. Thus,this paper uses the Least-Squares to calibrate the output characteristics. At first,a self-made pole is needed to measure load locations through marks on the rigid platform of force plate. Of course,by manually applying it to the rigid platform in arbitrary locations,a series of reference locations can be obtained. Based on the reference location data and imperfect force plate signals output data,a nonlinear model to calibrate the output characteristic of the COP is developed. Then,in view of least square error,the optimum solution of the model can be got. At last,the model is applied to the force plate through the software design. The results show that the calibration procedure reduces COP max absolute error and root-mean-square error by more than 90%,and the accuracy of the force plate is better than 1 mm.

force plate;calibration;center of pressure;least squares method

项目来源:国家自然科学基金项目(61074175)

2015-01-06 修改日期:2015-03-11

C:7230

10.3969/j.issn.1004-1699.2015.06.028

TP393

A

1004-1699(2015)06-0943-04