牺牲层二维腐蚀修正模型的研究*

俞佳佳,方玉明,蒋文涛,吉新村

(南京邮电大学电子科学与工程学院,南京 210003)



牺牲层二维腐蚀修正模型的研究*

俞佳佳,方玉明*,蒋文涛,吉新村

(南京邮电大学电子科学与工程学院,南京 210003)

针对氢氟酸腐蚀氧化硅,深入研究了牺牲层腐蚀的原理。牺牲层腐蚀主要受扩散机制影响。把二维扩散方程中的扩散系数看作溶液浓度和温度的函数,建立了二维腐蚀修正模型。利用有限差分算法求解扩散方程,并使用C语言编程实现了对单开口、内外拐角等多种复杂组合结构腐蚀过程的模拟,使用MATLAB软件绘制腐蚀图形,最后将模拟结果与实验结果进行了对比,验证了模型的合理性。

牺牲层腐蚀;二维腐蚀模型;扩散系数;计算机模拟

牺牲层技术是MEMS加工技术中的关键技术之一,通过牺牲层的释放形成空腔上膜或其他悬空结构,在MEMS器件加工中得到广泛运用。牺牲层工艺的优势在于与CMOS(Complementary Metal Oxide Semiconductor,互补金属氧化物半导体)工艺兼容,大批量制作可以降低加工成本[1-2]。同时,表面牺牲层技术不需要额外的掩膜版和光刻工艺,工艺简单,成本较低[3]。为了缩短研发周期和节约成本,计算机辅助设计变得越来越重要。由于MEMS器件结构和制造工艺的特殊性,MEMS与传统的电子系统在设计上存在很大差别,而现有的CAD(Computer Aided Design,计算机辅助设计)技术主要注重器件级和系统级仿真,对工艺级仿真涉及较少[4-5]。因此,牺牲层释放技术的模拟研究有着重要的意义。

现阶段典型工艺为在硅片上淀积氧化硅或者掺杂的氧化硅作为牺牲层,再通过牺牲层技术去掉牺牲层并形成自由悬空结构[6]。针对HF腐蚀氧化硅,前人建立了多种基于扩散方程的模型,多数是在一维空间进行研究的。Li Wen J在Liu[7]模型的基础上把模型从一维空间扩展到二维空间,实现了对单开口bubble结构的模拟[8]。但这些模型一般都只能模拟一些特殊结构,应用范围比较局限。此外,这些模型往往把扩散系数当作常数,这会造成一定的误差。

本文研究了基于二维扩散方程的二维腐蚀模型,并利用Topography模型[9]判断前端腐蚀情况,计算前端面的移动轨迹,实现了对多种复杂结构的模拟。同时,本文还将扩散系数是温度和腐蚀液浓度的函数运用到模型中去,得到更为精确的二维腐蚀修正模型。通过实验结果与模拟结果的对比证实了修正模型的合理性。

1 二维腐蚀模型

腐蚀机制由扩散机制和化学反应共同决定。腐蚀液从开口处扩散到前端面,再与前端面材料发生化学反应完成腐蚀。实验证明,一段时间后腐蚀主要受扩散机制的影响[9]。Masato Fujinaga的文章解释,化学腐蚀系统可分为三大部分,如图1(a)[9]:①腐蚀液层,②化学反应层,③材料层。在腐蚀液层中腐蚀主要受溶液扩散支配;化学反应层中腐蚀同时受溶液扩散和化学反应支配;材料层中,扩散与化学反应都被忽略。Masato Fujinaga的研究表明,区域②的化学反应非常快,近似于腐蚀液扩散到材料的前端面,材料即刻被腐蚀掉,因此腐蚀液层的浓度扩散等高线近似于腐蚀前端面行进的轨迹。

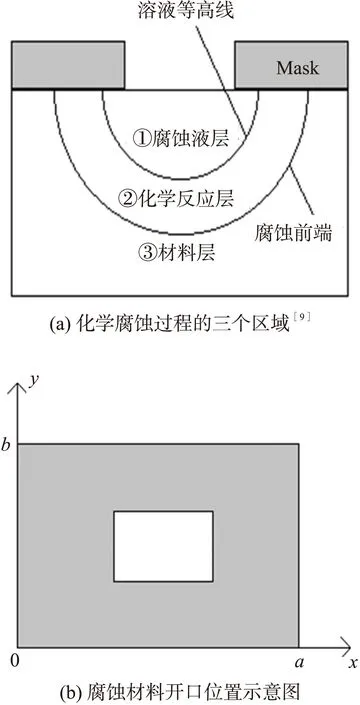
图1 化学腐蚀开口示意图

图1(b)为二维平面腐蚀示意图,待腐蚀材料的长度和宽度分别为a、b,中间白色区域为开口区域,注入腐蚀液。根据示意图,将一维扩散方程扩展到二维平面[10]:

(1)

式中:C=C(x,y,t)为腐蚀液t时刻,在(x,y)位置处的浓度;t≥0,0≤x≤a,0≤y≤b。D为腐蚀液的扩散系数。

求解此偏微分方程,需要给定方程的初始条件和边界条件。

初始条件为:

C(x,y,0)=0,(x,y)为不是开口位置的点坐标;

C(x0,y0,0)=C0,(x0,y0)为开口位置的点坐标,C0为开口处溶液浓度。

边界条件为:

C(0,y,t)=0,C(a,y,t)=0,C(x,0,t)=0,C(x,b,t)=0

(2)

由于开口处腐蚀液浓度是恒定的,腐蚀液在腐蚀二维平面呈余误差分布[11]:

(3)

式中:Cp为前端已经被腐蚀掉的单元的浓度。

为了便于分析,先从一维的情况进行研究。在一维空间内,溶液的分布为[10]:

(4)

溶液等高线的运动为

(5)

式中:erfc-1为余误差函数的逆。对上式两端进行求导,可以得到等高线的运动速率:

(6)

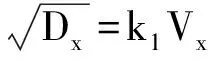
(7)

(8)

式中:k1,k2为常量。

溶液等高线向前推进的过程可以近似于腐蚀前端面的移动过程。由式(5)和式(6)可以得到等高线推进的距离为

(9)

对于二维空间上式同样适用[11],并且由于Dx,y=D,Vx,y=V,前端面移动的距离为

(10)

将上式代入式(3)可得[10]

(11)

上式表明,当腐蚀前端面溶液的浓度与已经被腐蚀掉的单元浓度的比值大于或等于0.32时,可以判定此单元已经被腐蚀掉,这样腐蚀前端面就向前推进了一步。

2 二维腐蚀修正模型

现有的多数模型把扩散系数D看作常数。大量实验表明,这种假设在较短的腐蚀时间(或者腐蚀长度)内和实验结果吻合较好,当腐蚀时间较长时,会和实验结果存在较大误差。扩散系数D可以看作温度和腐蚀液浓度的函数,但由于模拟过程中的温度不明确,本文主要对溶液浓度进行研究。

对于扩散系数和浓度的关系,Gordon提出了一个经验公式[12]:

(12)

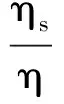
因此,式(12)可简化为:

(13)

根据Harned的研究[13]:

设溶液体积为1L,质量浓度为c,故有以下关系[14]:

(15)

(16)

故式(14)可化为:

(17)

于是:

(18)

故任意温度和浓度下的扩散系数为:

(19)

把上式运用到扩散方程(1)中去,可以得到更为精确的二维腐蚀修正模型。

3 实验验证和分析

对腐蚀模型的求解主要是对二维扩散方程(1)的求解。求解此偏微分方程,需要先把腐蚀平面划分为网格,求解每个小单元的量。本文采用交替方向隐式格式(ADI格式)求解。编程实现时,首先将腐蚀平面划分为网格,并对每一个单元进行标记,已经被腐蚀掉的单元记为0,没有被腐蚀掉的单元记为1。通过每一单元的浓度值计算扩散系数,再对扩散方程进行求解,得到下一时刻的浓度分布。根据式(11)判断此单元是否被腐蚀掉,更新标记。由此得到前端面的轨迹。

腐蚀实验结果引用自其他论文[10],腐蚀测试硅片的实验过程:首先,将硅片放置于丙酮中浸泡一段时间,去掉硅片上的光刻胶;然后用质量百分比浓度为30%的HF溶液对芯片进行腐蚀;腐蚀一定时间后用去离子水冲洗,酒精脱水晾干后置于显微镜下观察腐蚀轮廓。

将腐蚀平面划分为150×150的网格,时间步长为5s,空间步长为1μm。通过给定的参数和时间条件,用C语言编程,对腐蚀过程进行模拟,运行程序后输出数据文件,再使用MATLAB将输出的数据文件转化为模拟轮廓图。下面对实验结果和模拟结果进行了对比。

图2为单孔90μm×90μm的牺牲层结构,在开口尺寸分别为10μm、20μm和30μm,腐蚀20min的实验照片(a)、(b)、(c)和模拟结果(d)、(e)、(f)的对比图。表1为此结构腐蚀20min时的实验结果、二维腐蚀模型模拟结果,以及二维腐蚀修正模型的腐蚀结果对比。图3、图4分别是内拐角和外拐角腐蚀25min的模拟结果和实验结果对比图。表2列出了内外拐角腐蚀腐蚀25min时的实验结果、二维腐蚀模型模拟结果,以及二维腐蚀修正模型的腐蚀结果对比。

图2 边长分别为10 μm、20 μm和30 μm的方形开口结构腐蚀20 min的实验照片(a)、(b)、(c)和模拟结果(d)、(e)、(f)的对比

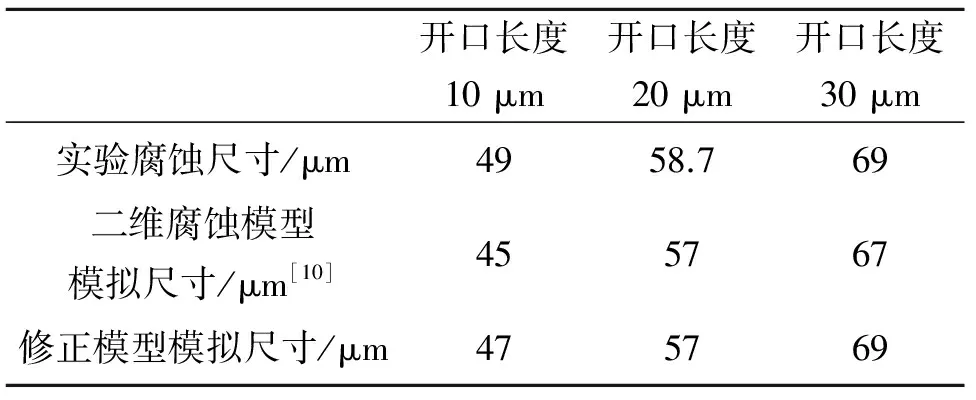
开口长度10μm开口长度20μm开口长度30μm实验腐蚀尺寸/μm4958．769二维腐蚀模型模拟尺寸/μm[10]455767修正模型模拟尺寸/μm475769

图3 内拐角腐蚀25 min结果示意图

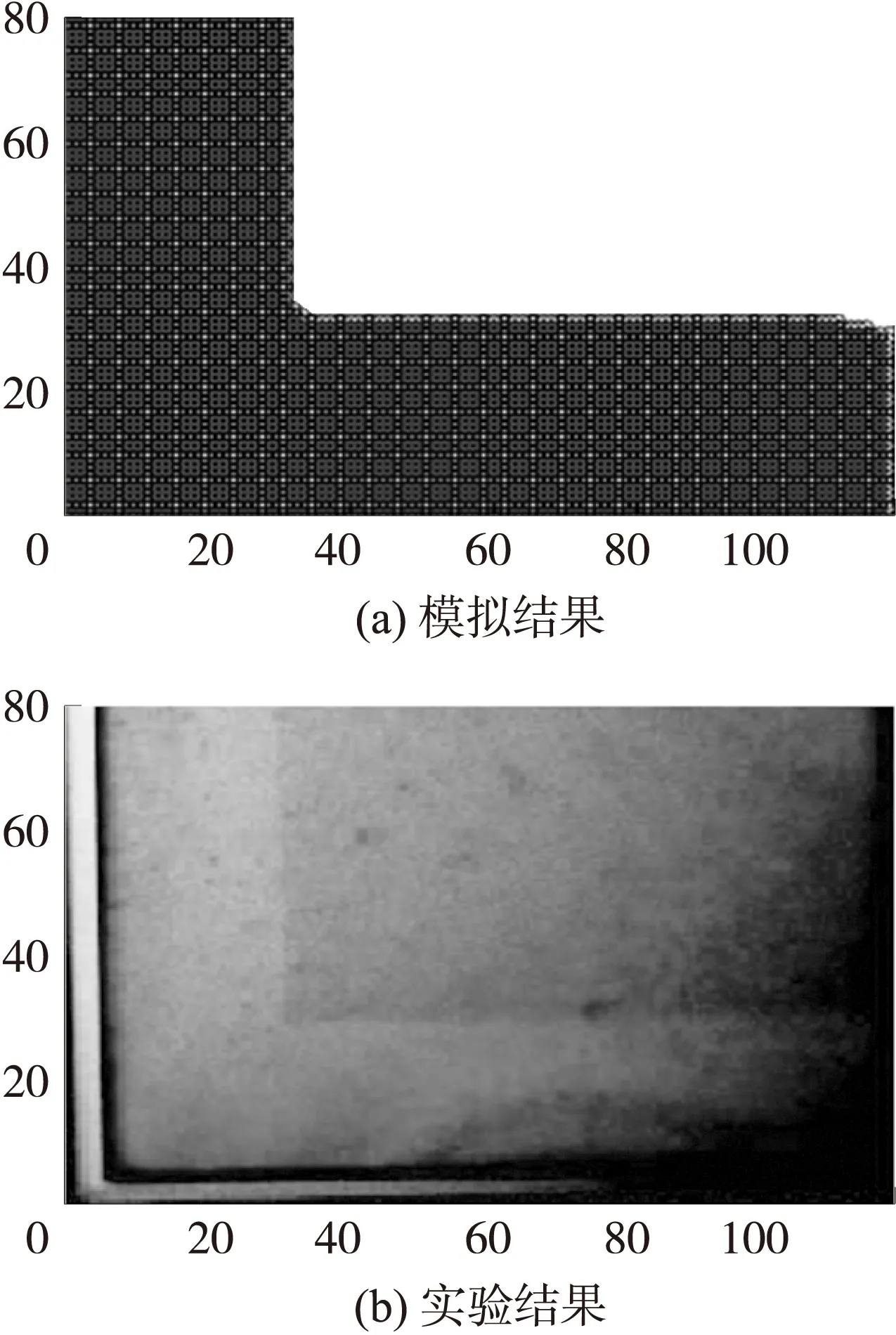
图4 外拐角腐蚀25 min结果示意图

从实验结果可以看出,修正模型比之前的二维腐蚀模型更为精确,与实验结果吻合更好,但腐蚀尺寸还存在一定的误差。主要原因是模型忽略了牺牲层材料和腐蚀溶液的化学反应对腐蚀的影响。而且本文只把扩散系数是溶液浓度的函数运用到了模型中,对于温度对扩散系数的影响没有考虑。此外,由于空间步长设为1 μm,模拟的精度也受到了影响。因此,要提高模拟的精度要从以上几个方面入手,建立更为精确的模型。

4 结论

牺牲层腐蚀主要受溶液扩散机制影响,扩散系数随着溶液浓度的变化而变化。本文基于现有的二维腐蚀模型,加入了溶液浓度对扩散系数的影响,建立了二维腐蚀修正模型,比原有模型更符合实际情况。文中利用有限差分算法求解扩散方程,并由Topography模型计算腐蚀前端面推进的情况。修正模型使用C语言编程实现对牺牲层腐蚀情况的模拟,并使用MATLAB软件输出腐蚀前端面的轮廓。通过腐蚀实验照片与模拟结果的对比,验证了修正模型的准确性。

[1] 黄占喜,吴亚明. 三维掩膜硅各向异性腐蚀工艺释放微悬空结构[J]. 微纳电子技术,2011,48(5):326-332.

[2] 徐永青,杨拥军. 硅MEMS器件加工技术及展望[J]. MEMS器件与技术,2010,47(7):425-431.

[3] 申宁,余隽,唐祯安. 基于CMOS工艺钨微测辐射热计阵列集成芯片的设计与制作[J]. 传感技术学报,2014,27(6):725-729.

[4] Li J,Liu Y,Ling H. Development of Solid-Based Modeling System for Surface Micromachined MEMS[C]//International Conference on Computer Research and Development. Shanghai:IEEE,2011:297-301.

[5] 胡伟,胡国清,魏昕. 微机电系统CAD研究及发展现状[J]. 压电与声光,2010,32(4):682-691.

[6] 揣荣岩,王健,代全,等. 基于牺牲层技术的高过载压力传感器芯片[J]. 传感技术学报,2014,27(12):1615-1621.

[7] Liu J,Tai Y,Lee J,et al. In Situ Monitoring and Universal Modelling of Sacrificial PSG Etching Using Hydrofluoric Acid[C]//Micro Electro Mechanical Systems,1993,MEMS’s93,Proceedings An Investigation of Micro Structures,Sensors,Actuators,Machines and Systems. IEEE. IEEE,1993:71-76.

[8] Li Wen J,Shih Jack C,Mai John D. Nμmerical Simulation For The Sacrificial Release of MEMS Square Diaphragms[C]//Technical Proceedings of the 1998 International Conference on Modeling and Simulation of Microsystems,UC-Los Angeles:NSTI,1998:59-64.

[9] Fujinaga M,Kotani N,Kunikyo T,et al. Three-Dimensional Topography Simulation Model:Etching and Lithography[J]. IEEE Transactions on Electron Devices,1990,37(10):2183-2192.

[10] 李艳辉. 牺牲层腐蚀模型与模拟研究[D]. 南京:东南大学电子科学与工程学院,2006.

[11] Salo T,Vancura T,Baltes H. Modelling of Sacrificial Aluminium Etching in Complex Geometries[J]. Journal of Micromechanics and Microengineering,2004,14(9):123-127.

[12] Gordon A R. The Diffusion Constant of an Electrolyte,and Its Relation to Concentration[J]. The Journal of Chemical Physics,1937,5(7):522-526.

[13] Harned H S,Owen B B. The Physical Chemistry of Electrolytic Solutions[J]. Journal of Chemical Education,1944,21(7):363.

[14] 吴昌聚. 微纳结构牺牲层腐蚀及其模型研究[D]. 浙江:浙江大学信息科学与工程学院,2006.

俞佳佳(1991-),女,硕士研究生,主要研究方向为MEMS工艺的研究与模拟,yogaaa@163.com;

方玉明(1975-),女,汉族,江苏人,博士,毕业于东南大学电子科学与工程学院MEMS教育部重点实验室,南京邮电大学电子科学与工程学院微电子技术系教授。主要研究方向为微电子学及MEMS系统研究,fangym@njupt.edu.cn。

Study of Amended 2-D Model of Sacrificial Layer Etching*

YUJiajia,FANGYuming*,JIANGWentao,JIXincun

(Electronic Science and Engineering,Nanjing University of Posts and Telecommunications,Nanjing 210003,China)

Aimed at silicon oxide etched by HF,deeply study is carried on on sacrificial layer etching. Sacrificial layer etching is affected mostly by the diffusion of etching solution. The paper regards the diffusion coefficient as a function of solution concentration and temperature,and constructs the amended 2-D etching model. The numerical algorithm of finite-difference method is given for the diffusion equation. The simulation program which can simulate different complex sacrificial structures including single open,inside corner and outside corner is implemented. Language C is used to simulate the etching process,and MATLAB is used to graphing. Through contrasting the simulation results and the experiment ones,the rationality of the model is verified.

sacrificial layer etching;2-D etching model;diffusion coefficient;simulation with computer

项目来源:江苏省普通高校专业学位研究生科研实践计划项目(SJLX_0372);江苏省自然科学基金项目(BK20131380,BK20130880)

2015-01-08 修改日期:2015-02-26

C:2550

10.3969/j.issn.1004-1699.2015.06.006

TN402

A

1004-1699(2015)06-0809-05