基于PSO算法集成神经网络的多元有害气体检测系统*

龚雪飞,刘 萍,简家文

(宁波大学信息科学与工程学院,浙江 宁波 315211)



基于PSO算法集成神经网络的多元有害气体检测系统*

龚雪飞,刘 萍,简家文*

(宁波大学信息科学与工程学院,浙江 宁波 315211)

针对目前常见的多元有害气体检测问题,搭建了一套基于传感器阵列和集成神经网络相结合的多元有害气体检测系统。为了提高该系统的稳定性和预测精度,提出使用粒子群算法(PSO)优化集成神经网络的权重系数的方法,即利用PSO的全局搜索能力,对该系统的集成神经网络权重系数进行全局优化,再以优化后的权重系数实现多个神经网络的结论结合。该系统对传感器阵列的4种混合有害气体的响应信号进行回归分析。结果显示,该系统PSO算法的集成神经网络预测的平均相对误差小于1%,网络具有更强的稳定性和泛化能力。

集成神经网络;PSO;传感器阵列;多元有害气体检测

随着近代工业规模不断扩大,在此过程中产生了大量的NOx、CO、CO2等有毒、有害气体,O2作为衡量大气的有效标杆,因此,检测上述气体浓度对改善大气环境具有现实意义[1]。传统传感器气体检测都是基于单一气体的主成分特征,但是当多种有害气体发生混合时,气体之间相互干扰造成主成分特征丢失,导致检测无法正常完成[2]。针对这一缺陷,将气敏传感器阵列和模式识别技术相结合构建的多元有害气体检测系统,既能够同步检测多元气氛又能够很好地解决气敏传感器的交叉敏感问题[3-5]。

为了提高模式识别的预测精度,神经网络集成已成为一个研究热点,近几年对神经网络集成的研究主要集中在两个方面,即如何构造集成中的各个神经网络以及如何集成各个体神经网络的输出[6-8]。本文提出使用PSO优化集成神经网络的权重系数的算法,以实现集成多个神经网络的输出。并对比经典Adaboost算法的集成神经网络和PSO算法的集成神经网络预测的精确度,分析两种网络的性能。

1 检测系统与实验

1.1 检测系统

本文中的有害气体检测系统是模拟人的嗅觉系统对被测气体进行感知、分析和识别,由气敏传感器阵列、传感器信号预处理、阵列信号采集和模式识别4部分组成的检测系统,其原理如图1所示。

图1 检测系统原理图

图2 检测系统硬件模块

本文选用A2-O2氧气传感器、TGS4160二氧化碳传感器、TGS2201一氧化碳传感器、NO2-AE二氧化氮传感器、HTG3515温湿度传感器组成阵列,如图2(a)所示。利用动态配气的方法将4种的标准气体经过4台精密流量控制器进行流量调节、配比、混合,模拟实现多元有害气体混合的环境,后流入封闭的测试装置,如图2(b)所示。

为了便于对传感器信号的采集,需对传感器信号进行预处理,预处理后输出的信号均为模拟电压。之后使用美国NI公司的PCI 6221采集板卡实现传感器阵列信号采集。

由于选取的传感器输出参数不同,因此针对每个传感器设计信号预处理电路,主要将传感器输出信号进行流压转换,信号放大,滤波等处理。图3(a)是电化学传感器(氧气传感器、二氧化氮传感器),图3(b)是半导体传感器(二氧化碳传感器、一氧化碳传感器)传感器信号预处理电路。

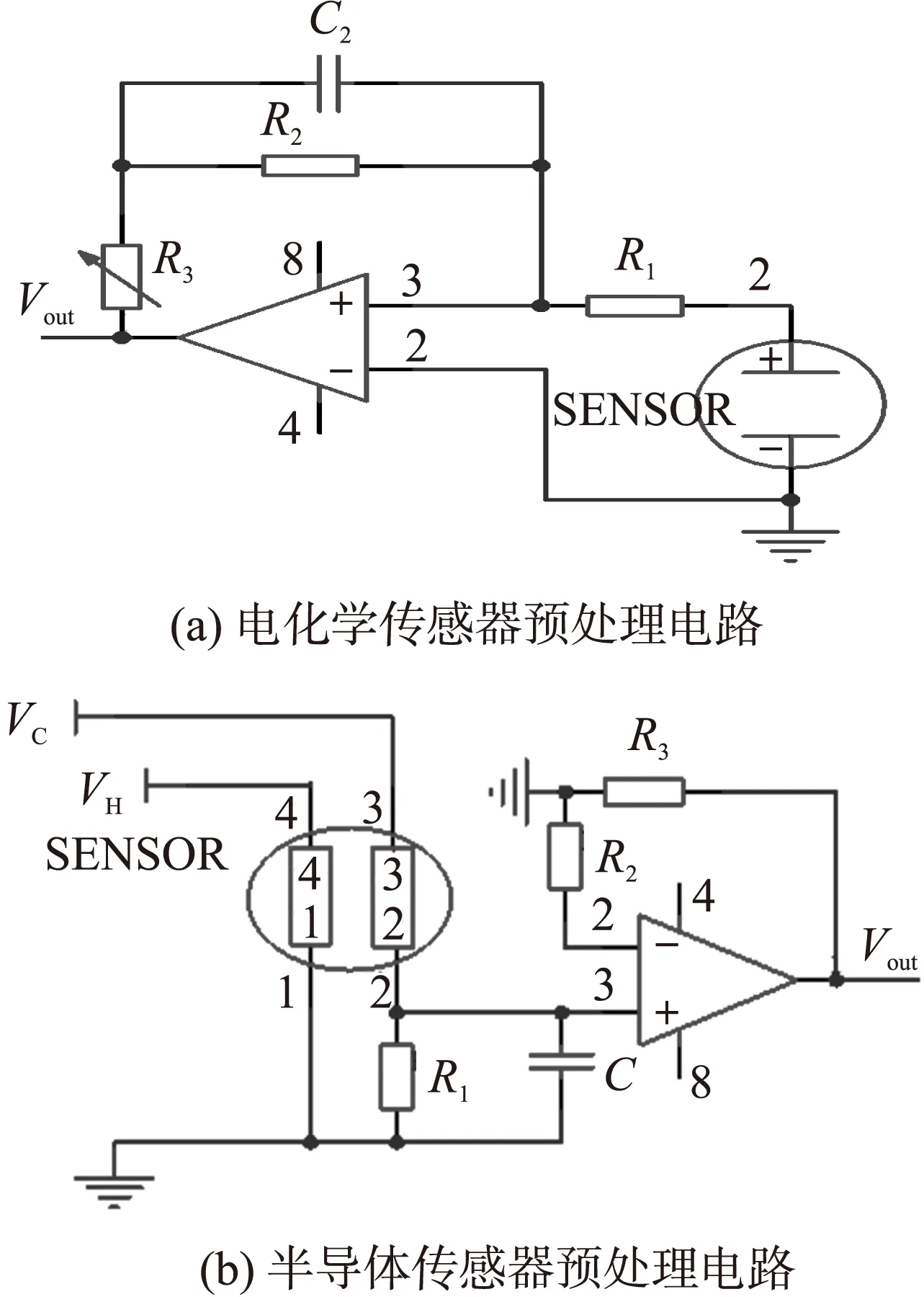
图3 传感器预处理电路

图3(a)中,传感器输出电流信号Iin,R2为一个定值反馈电阻,R3表示可调电阻,R2、C2构成低通滤波器,R2、R3及运算放大器构成反向放大电路并进行流压转换:

Vout=-Iin*(R2+R3)

(1)

图3(b)中,VC表示整个回路电压,VH是传感器上加热电压,R1与传感器内阻Rs构成分压电路,R2、R3及运算放大器构成电压放大电路:

Vout=VC*R1*(R2+R3)/(R1+Rs)*R2

(2)

1.2 实验过程

本文根据工业排放规定及传感器敏感范围选定气体体积分数范围:O2[18%～22%]、NO2[0～2.5×10-4]、CO[0～1.0×10-3]、CO2[0～5.0×10-3],配制了510组混合气体,尽可能覆盖整个被测空间。将配好的气体逐一通入测试装置,气体与传感器阵列反应,采集传感器响应信号,得到510组样本数据:X(气体浓度)-Y(传感器响应值)。

2 PSO优化集成神经网络算法

2.1 PSO算法

粒子群(PSO)是一种新颖的演化算法,该算法通过粒子间的相互作用在复杂搜索空间中发现最优区域,具有训练精度较高、收敛性良好等优点[9-10]。粒子群算法的具体实现如下:假设在一个D维的目标搜索空间中,有m个粒子组成一个群体,其中第i个粒子的位置为xi=(xi1,xi2,…,xiD) i=1,2,…,m;其速度也是一D维向量:vi=(vi1,…,vi2,viD) i=1,2,…,m;第i个粒子迄今为止搜索到的最优位置为pi=(pi1,pi2,…,piD) i=1,2,…,m;整个粒子群搜索到的最优位置为pg=(pg1,pg2,…,pgD) g=1,2,…,m;粒子更新公式如下:

vid(t+1)=

w*vid(t)+c1r1(pid-xid(t))+c2r2(pgd-xid(t))

(3)

xid(t+1)=xid(t)+vid(t+1) d=1,2,…,D;

(4)

式中:c1、c2均为学习因子,非负常数;r1、r2均为服从[0-1]的均匀分布随机数;vmax为非负数;w为惯性权重函数;STEP、STEPmax分别为当前迭代步数和最大迭代步数。

图4 PSO算法的集成神经网络算法流程图

2.2 PSO优化集成神经网络

1990年,Hansen和Salamon证明:可以简单地通过训练多个神经网络并将其结果进行合成,显著地提高神经网络系统的泛化能力。1996年Sollich和Krough的定义,神经网络集成是用有限神经网络对同一个问题进行学习,集成在某输入示例下的输出由构成集成的各神经网络在该示例下的输出共同决定。神经网络集成研究的关键问题是:在确定集成神经结构后,如何集成各个体神经网络的输出[11-12]。

因此,本文首先通过改变BP神经网络隐藏层神经元数来构造具有差异性的集成神经网络的个体网络;其次,优化集成神经网络的集成度;最后,使用PSO算法优化集成神经网络的权重系数,以实现集成多个BP神经网络的输出,构建一个性能极好的集成神经网络。PSO优化集成神经网络算法流程,如图4所示。

3 实验结果与算法性能分析

3.1 交叉敏感性测试

将本测试系统的NO2传感器分别在4.0×10-5～2.0×10-4NO2+余N2和参杂有一定浓度(CO、CO2)的4.0×10-5～2.0×10-4NO2+余N2混合气体中进行测试,呈现出如图5所示的特性曲线。

图5 NO2传感器在不同气氛中输出对比图

从图5可以得到,虽然CO2对NO2基本不产生干扰,但不同浓度的CO对NO2表现出不同的干扰特性。因此可以得出采用单一传感器由于交叉干扰的问题无法实现对多种共存气体的精确测试。

3.2 PSO优化集成神经网络参数学习

对样本数据进行归一化,随机取450组样本数据作为训练样本输入上文所构建的集成神经网络进行训练,训练完成后保存集成神经网络参数,完成集成神经网络的建立。剩余60组样本数据测试该网络性能,计算网络的预测误差。通过不断训练学习,调整集成神经网络参数,从而得出一个针对本实验数据能够快速收敛并且进行准确预测的集成BP神经网络。下面将分别介绍几个参数的调整实验。

3.2.1 BP神经网络参数调整

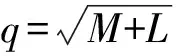
网络集成时,既要保证个体网络的预测精度,又要保证个体之间的差异性,由表1可知,在隐藏层神经元数大于7时,各组气氛能达到较小的平均相对误差较小。因此,构建集成网络时将BP神经网络隐藏层神经元数设成不同数值(8～14),以保证网络组中个体网络的差异性。

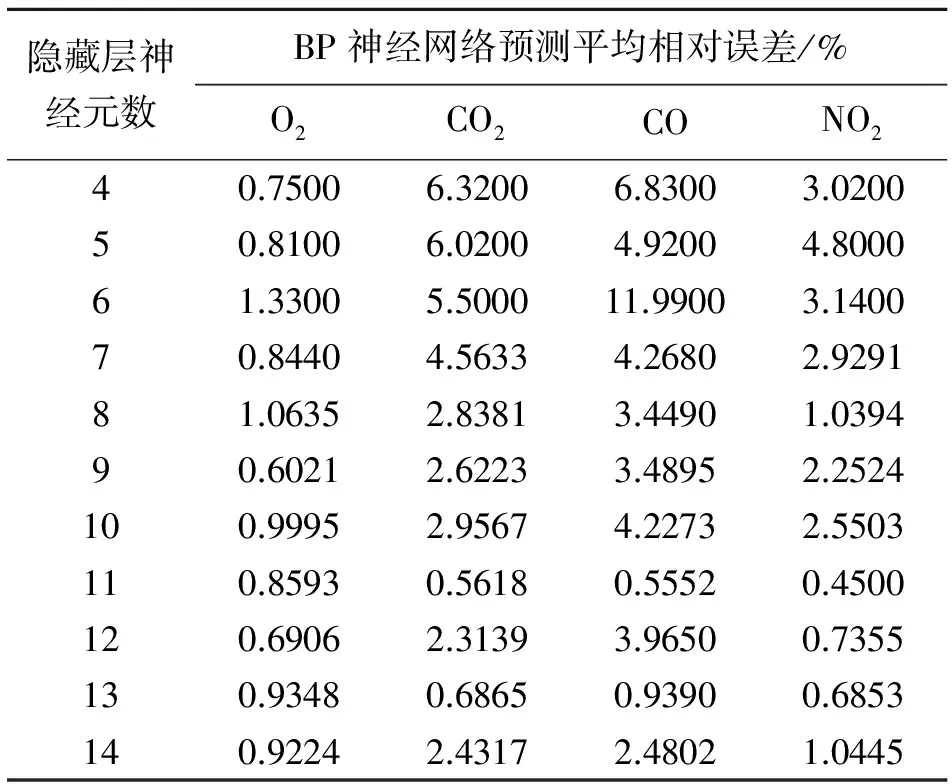
表1 隐藏层不同神经元数的网络预测平均相对误差

注:平均相对误差=(|网络实际输出-期望输出|)/期望输出×100%;

3.2.2 网络集成度参数调整

上文对集成神经网络的差异性个体网络组建进行了阐明,接下来介绍集成神经网络的集成度参数调整。在神经网络集成的规模较大,即个体网络较多时,对结论的权进行优化没有好处,适于使用简单平均等结论合成方法;而在神经网络集成的规模较小,即个体网络较少时,对结论的权进行优化将提高学习系统的泛化能力。因此网络的集成度要选择恰当,这就需要在训练过程中,调整网络集成度。表2为网络集成度取不同值的条件下,所得到的预测平均相对误差。

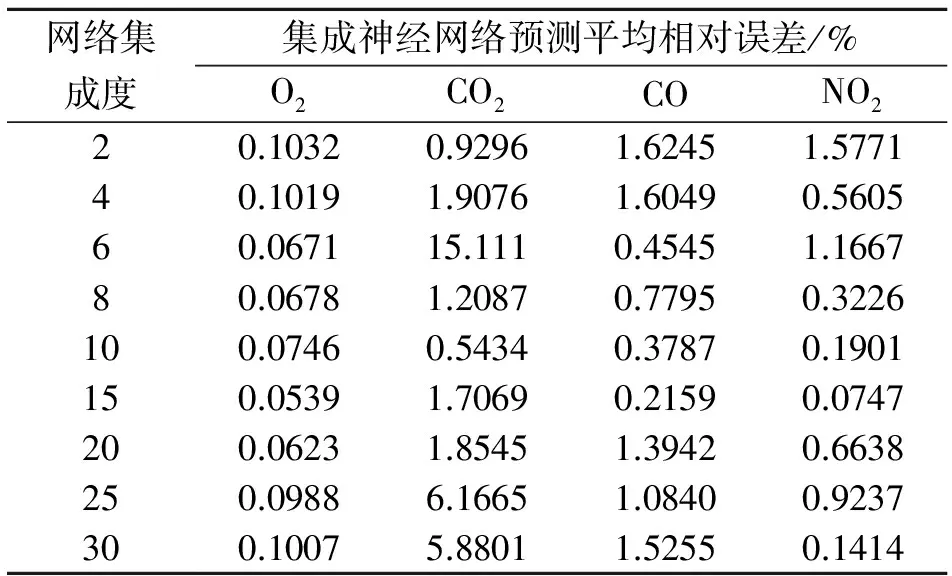
表2 不同网络集成度的网络预测平均相对误差

由表2可知,在集成神经网络集成度为10时,各组气氛的预测平均相对误差最小。

3.2.3 PSO参数调整

为了提高集成神经网络的泛化能力和预测精度,本文利用PSO的全局搜索能力,对该网络权重系数进行全局优化,再以优化后的权重系数实现多个神经网络的结论结合。随机初始化粒子并形成粒子群体,将粒子映射为集成神经网络权重。由于粒子群的规模,不仅影响搜索精度,还影响算法的收敛速度,因此,在保证搜索精度的情况下,尽量取较小规模的粒子群[14]。本实验通过改变粒子群体规模,寻找最优的粒子群的规模。表3为PSO不同粒子群规模时,网络所得到的预测平均相对误差。

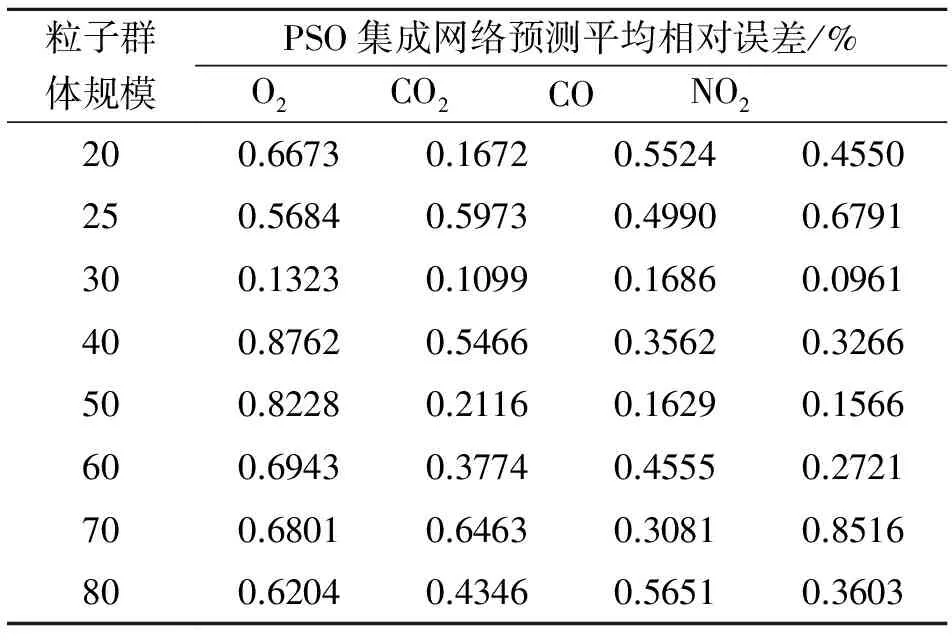
表3 不同粒子群体规模的网络预测平均相对误差

由表3可知,在PSO粒子群规模为30时,既保证了各组分气体具有较小的相对误差,又保证了较快了收敛速度。

3.3 实验结果及对比分析

将3.2学习好的参数保存,并建立PSO算法的集成神经网络,取上节450组训练样本输入网络训练,训练完成后保存该网络参数,使用剩下的60组样本进行测试,记录测试结果。为了比较网络的性能,本文同时采用经典Adaboost集成神经网络在相同情况下进行训练。即采用同样的样本数据进行训练网络,同样的测试样本进行测试。两种神经网络测试的结果见表4。

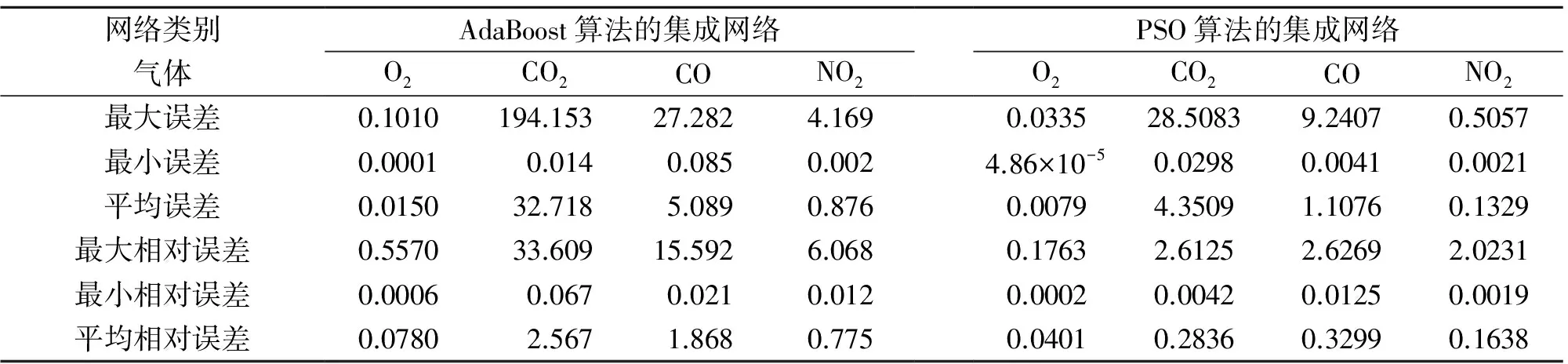
表4 AdaBoost、PSO算法的集成神经网络预测结果误差比较

注:①误差=|网络实际输出-期望输出|;②相对误差=(|网络实际输出-期望输出|)/期望输出×100%。

从表1中可以得到:在相同的训练样本时,PSO算法的集成神经网络较经典Adaboost集成神经网络具有更小的预测误差,PSO算法的集成神经网络预测的平均相对误差均小于1%;在网络训练时,有效避免训练时进入局部最优解,提高了预测系统的稳定性。

4 结论

针对多元有害气体检测问题,本文利用PSO算法优化集成神经网络的模型来实现对传感器阵列信号分析,从实验结果可以得到如下结论:使用传感器阵列检测多元气体能够消除气体交叉响应的影响,摄取更多混合气体组分信息和浓度信息;将集成神经网络和传感器阵列技术组合的检测系统对多元有害气体的检测取得了较好的效果,在定量检测实验中,预测的平均误差百分比均小于1%;PSO算法的集成神经网络的算法要较经典Adaboost集成神经网络的算法能够达到更小的预测误差,并且建模稳定性高。

[1] Yamazoe N,Miura N. Development of Gas Sensors for Environment Protection[J]. IEEE Tran on Comp Pack and Manuf,1995,18(2):252-256.

[2] 郑杰. 混合有毒气体检测算法研究[J]. 计算机仿真,2011,28(8):413-416.

[3] Belhouari S B,Bermak A,Wei G,et al. Gas Identification Algorithms for Microelectronic Gas Sensor[J]. Instrumentation and Measurement,2004(5):584-587.

[4] 张覃轶. 电子鼻:传感器阵列、系统及应用研究[D]. 华中科技大学,2005.

[5] 尤丽华,吴静静,王瑶. 基于模拟退火优化BP神经网络的pH值预测[J]. 传感技术学报,2014,27(12):1643-1648.

[6] 孙凌逸,黄先祥,蔡伟,等. 基于神经网络的无线传感器网络数据融合算法[J]. 传感技术学报,2011,24(1):127.

[7] 周志华,何佳洲,陈世福. 神经网络国际研究动向[J]. 模式识别与人工智能,2000,13(4):415-418.

[8] Zhou Zhihua,Wu Jianxin,Tang Wei. Ensembling Neural Networks:Many could be Better Than All[C]//Artificial Intelligence,2002,137(1-2):239-263.

[9] 孙艳梅,刘树东,苗凤娟,等. 基于PSO的BP神经网络在压力传感器温度补偿中的应用[J]. 传感技术学报,2014,27(3):342-346.

[10] Wang Hongfeng,Wang Na,Wang Dingwei. A Memetic Particle Swarm Optimization Algorithm for Multimodal Optimization Problems[C]//Chinese Control and Decision Conference,2011,3839-3845.

[11] 周志华,陈世福. 神经网络集成[J]. 计算机学报,2002,25(1):1-7.

[12] 傅强,胡上序,赵胜颖. 基于PSO算法的神经网络集成构造方法[J]. 浙江大学学报:工学版,2004,38(12):1596-1600.

[13] Dong C,Dong L,Yang M. The Application of the BP Neural Network in the Nonlinear Optimization[J]. Advances in Intelligent and Soft Computing,2011,78:727-732.

[14] 张雯雰,王刚,朱朝晖,等. 粒子群优化算法种群规模的选择[J]. 计算机系统应用,2010,19(5):125-128.

龚雪飞(1989-),男,宁波大学硕士研究生,主要研究方向为传感器阵列信号融合,1025500740@qq.com;

简家文(1967-),男,宁波大学教授、博士生导师,主要研究方向为气体敏感材料与传感器制备、传感器信号处理以及智能仪表,jianjiawen@nbu.edu.cn。

Based on the Integrated Neutral-Network Optimized byPSO Multiple Harmful Gas Detection System*

GONGXuefei,LIUPing,JIANJiawen*

(School of Information Science and Engineering,Ningbo University,Ningbo Zhejiang 315211,China)

Aiming at the common multiple harmful gas detection problem,a gas detection system was developed by combining a sensor array with the integrated neutral-network. In order to improve stability and prediction accuracy of the system,put forward using particle swarm optimization(PSO)to optimize the weight coefficient of integrated neutral-network,namely,utilizing the global search ability of PSO to global optimization of the network weight coefficient,then use the weight coefficient implement multiple conclusions combination of neural network. This system is performing regression analysis on the response signal of four harmful gases mixture measured by sensor array. The results show that the prediction average relative error of the integrated neutral-network optimized by PSO was found to be within 1%,and the network has better stability and generalization ability.

integrated neutral-network;PSO algorithm;sensor array;mix harmful gas detection

项目来源:国家自然科学基金项目(61471210);浙江省科技厅重大科技专项重点工业项目(2011C16037);浙江省宁波市科技局自然科学基金项目(2013A610002)

2014-12-15 修改日期:2015-03-03

C:1295;6150P;7230

10.3969/j.issn.1004-1699.2015.06.027

TP183;TP212

A

1004-1699(2015)06-0938-05