某铁矿无底柱分段崩落法最优结构参数研究

冯浩楠，舒太镜，郭建来

（河北邯邢矿冶设计院有限公司，河北邯郸056001）

某铁矿无底柱分段崩落法最优结构参数研究

冯浩楠，舒太镜，郭建来

（河北邯邢矿冶设计院有限公司，河北邯郸056001）

分段高度、进路间距及崩矿步距是影响无底柱分段崩落法的三个重要因素。结合江西某铁矿生产条件，运用PFC3D数值模拟软件，对通过正交组合试验确定的9组不同的结构参数模型进行放矿模拟。对试验结果进行分析，推荐该铁矿采场采用的最优结构参数为分段高度14m、进路间距16m、崩矿步距3m。

无底柱分段崩落法；正交试验；数值模拟；采场结构参数；PFC3D

无底柱分段崩落法是一种广泛应用于金属矿山尤其是铁矿山的高效安全的采矿方法。该采矿方法的核心是采场结构参数的选取与覆岩下的放矿管理［1］。此二者的关系是相辅相成的，一般情况下，我们需要根据崩落矿岩的移动规律，结合矿体的赋存条件，获得满足采场的最优结构参数，减小矿石的损失贫化。为了提高矿山的生产能力，当前研究及发展趋势表明［2－5］，无底柱分段崩落法的结构参数正朝着高分段大间距方向发展。江西某铁矿属变质火山—沉积型铁矿床，倾角50°～70°，矿层沿走向呈带状，平均厚度14m。本文作者以该铁矿为例，对几组高分段大间距结构参数进行正交组合试验设计，然后采用数值模拟方法，对设计所选择的采场结构参数进行研究，以期获得满足该矿山的合理结构参数值。

1 正交组合试验设计

正交组合试验设计是在各因素试验范围内选取试验点，根据均衡和正交试验原理，采用最合理的试验组合获得满意的试验效果。大量研究［6－8］表明，影响无底柱分段崩落法回收指标的主要因素为分段高度、进路间距和崩矿步距。

本次模拟试验选定分段高度（x1）、进路间距（x2）和崩矿步距（x3）三个因素进行试验，考虑到矿山设备的综合利用能力及放矿管理能力，选取三组不同的正交试验因子水平，见表1。据各因子水平的正交组合设计，需进行三因素三水平L9（34）即9组模型试验。

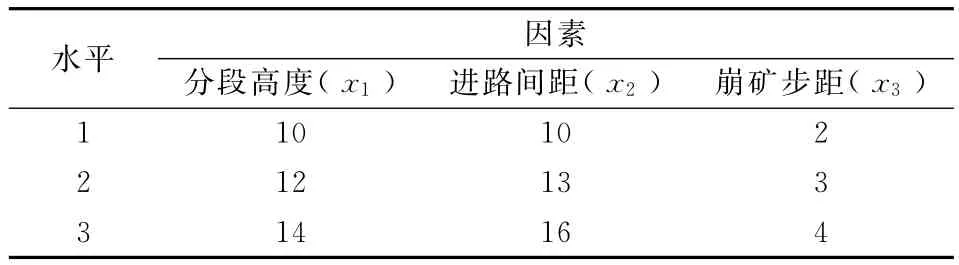
表1 正交试验因素水平表Table 1 Orthogonal experiment factor level

2 数值模拟试验

2．1 模拟软件

PFC是著名学者Cundall根据离散元理论开发的用于分析细观结构力学性态的一款数值模拟软件，其基本的思想是利用粒子及粒子间最基本的力学关系即牛顿第二定律来描述介质的力学性态［9］，通常采用圆形或球形的离散单元来模拟颗粒介质的运动及其相互作用。无底柱分段崩落法崩落的矿石及覆岩可以近似看作离散的球形颗粒介质，其放矿形式便可以利用PFC软件进行模拟。目前，PFC软件包括PFC2D和PFC3D，为了全面分析分段高度、进路间距及崩矿步距等因素的影响，并详细清楚地展示无底柱分段崩落法放矿时矿石的运动规律，本文利用PFC3D软件进行无底柱分段崩落法的放矿模拟。

2．2 数值建模

由正交组合设计可知需建9组不同结构参数模型并进行数值计算，模型按采场的实际大小而定，现根据该矿的矿体赋存条件及设备生产能力，以其中的一组结构参数模型详细介绍：分段高度10m，进路间距13m，进路尺寸（宽×高）取3m×3m，采场宽度14m。按照PFC3D的命令形式，建立该组的多分段立体模型，模型结构如图1。

2．3 颗粒参数选取

根据矿山实际情况，通过查阅资料及一定的室内测试和计算，并参考相似的研究成果［10－11］，获得本次模拟所需要的颗粒参数值。本次模拟生成的球形颗粒有岩石和矿石两种，其中首采分层的岩石和矿石界面可近似为水平接触。该模型需要用到的建模参数主要有颗粒半径；颗粒或墙的法向刚度；颗粒或墙的切向刚度；颗粒间或颗粒与墙之间的摩擦因数；颗粒密度大小及颗粒颜色，计算参数见表2。

表2 数值模拟计算参数表Table 2 Numerical simulation parameters

2．4 放矿模拟

本次模拟采用20%的现行截止品位作为控制条件进行多孔放矿，放矿初期放出的基本为纯矿石，矿岩界面随着平缓下移，下移到某一高度后，开始出现凹凸不平的现象，随着放矿的继续，凹凸不平现象愈加明显，当矿岩界面到达漏孔水平时，在漏孔间形成脊部残留，此脊部残留高度即为岩石开始混入高度，再继续放矿时，矿石出现贫化，放到截止品位后停止放矿。放矿截止品位计算公式见式（1）。

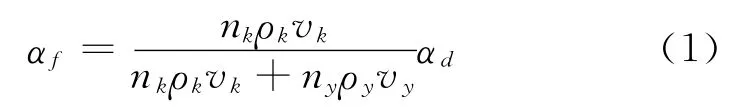
式中：αf—放矿截止品位；nk—矿石颗粒个数；ny—岩石颗粒个数；ρk—矿石密度；ρy—岩石密度；vk—矿石颗粒体积；vy—岩石颗粒体积；αd—矿石地质品位。

据表2中的矿岩颗粒半径计算出矿岩的颗粒体积，放矿截止品位αf为20%，矿石地质品位αd为35%，由此得用矿石颗粒与岩石颗粒个数之比表示的放矿截止条件为nk∶ny＝4∶1。在模拟放矿的过程中，放矿顺序是同一分段的放矿口同时放矿，当该分段放出矿石颗粒与岩石颗粒之比达到4∶1时，停止该分段放矿，进行下一分段放矿，每一组试验结果将根据两个分段的放矿数据，获得平均的矿石回收率与贫化率。为了提高计算机的运行速度，本次模拟矿岩颗粒各自采用了平均半径，模拟时，先生成上下两层小直径的岩石与矿石颗粒，然后利用膨胀系数扩大半径，此过程将在模型内产生初始应力场，模型内的非均匀应力可通过循环来消除。装矿及放矿过程图如图2～4。

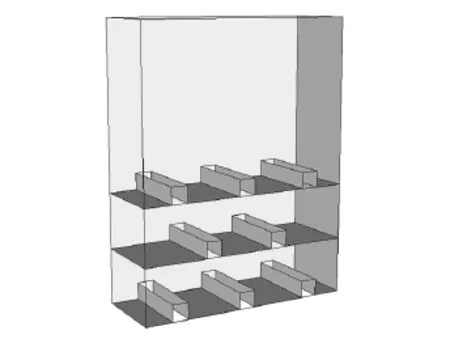
图1 数值模拟立体模型Fig．1 Numerical simulation three－dimensional model

3 试验结果分析

图2 初始装矿模型Fig．2 Initial mining model

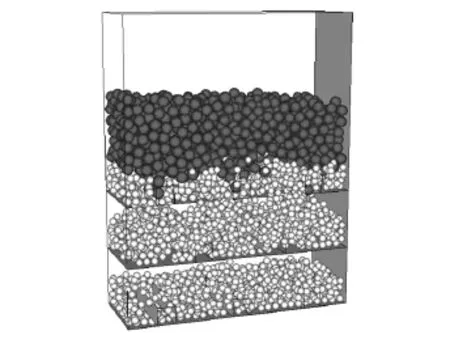
图3 第一分段放矿模拟Fig．3 Ore drawing simulation of the first sublevel

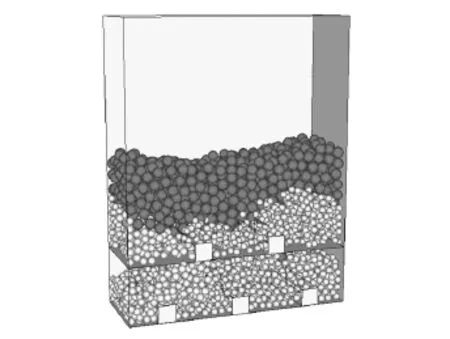
图4 第二分段放矿模拟Fig．4 Ore drawing simulation of the second sublevel

在实际生产过程中，由于进行原位试验是比较困难的，因此考虑利用数值模拟方式来探讨无底柱分段崩落法放矿效果，虽然每种因素对放矿效果都会产生一定的影响，但是在模拟的过程中同时考虑到所有影响因素也是不现实的，现只对分段高度、进路间距和崩矿步距三个重要因素进行组合模拟试验。通过对9组模型进行试验，经统计获得了9组不同的矿石回收率及贫化率数据，试验结果详情见表3。对9组试验的矿石回收率与贫化率数据进行分析比较，见图5。

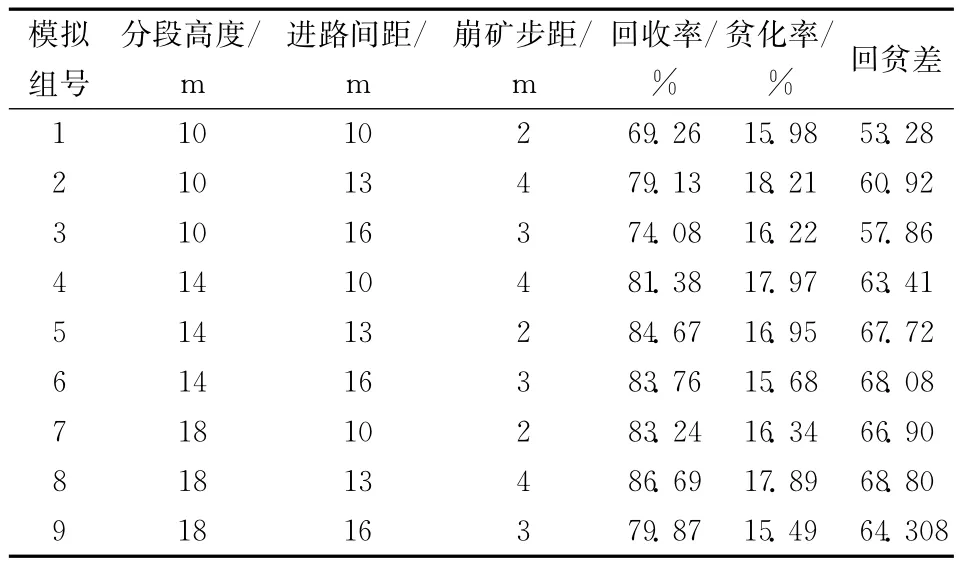
表3 数值模拟放矿结果表Table 3 Numerical simulation ore drawing result

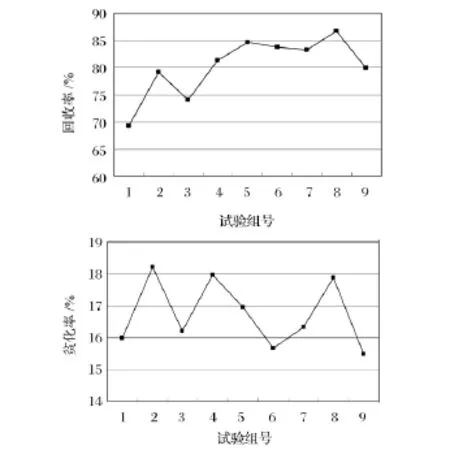
图5 9组模拟试验回收率与贫化率比较Fig．5 Comparison of recovery rata and dilution rate in 9groups of simulation test

通过对9组试验的矿石回收率与贫化率数据分析比较，其中不同参数结构的模型矿石回收率变化范围较大，但大部分回收率仍然为80%～85%，与一般国内采用无底柱分段崩落法的矿山回收率相符；贫化率较25%～30%的国内贫化率小。造成该结果的主要原因一是在实际的生产过程中，矿体中是含有夹石的，而在数值模拟中这部分夹石是没有考虑到的，因此贫化率较小；二是在实际生产过程中，有大量小颗粒岩石的混入矿体及小颗粒矿石损失，而模拟采用的是大小均质的球体，这也使得模拟获得的贫化率会较实际生产中小。

该9组模型除了结构参数不同，模拟过程中的球体的初始条件、球体的物理力学参数及放矿步骤都是相同的，因此模拟结果的变化基本是由结构参数引起的，模拟结果具有可比性。首先，根据回贫差（回收率与贫化率的差值）大小判断采场结构参数的优劣，一般情况下，回贫差越大，则结构参数越优。通过对比9组试验的矿石回收率可知，采场的分段高度与矿石的回收率具有一定的递增趋势，因此结构参数考虑分段较高的4至9组；在4至9组中，第4、5、6、7、8组回贫差较大，结构参数较优，但考虑到该铁矿设备条件及采准工程情况，剔除第7、8两高分段组；分析比较第4、5、6三组，第4组贫化率太大，可以剔除，尽管第6组回收率稍小一些，但无论是矿石贫化率还是回贫差，第6组都占优势，剔除第5组。综上所述，推荐采用分段高度14m、进路间距16m、崩矿步距3m的采场结构参数。

4 结论

1）数值模拟结果中，矿石回收率基本满足国内一般指标范围而贫化率指标偏低，其原因是放矿过程中未考虑矿体中夹石的影响，且模拟采用的是均匀大小的球体，未考虑小颗粒岩石的混入及小颗粒矿石的损失，但总体上不影响多组方案的比较分析。

2）在一定范围内，随着分段高度的增大，矿石回收率总成增大趋势，分段高度对无底柱分段崩落法的影响较进路间距及崩矿步距更大。

3）运用PFC3D数值模拟对9组三因素不同结构参数模型进行放矿模拟，结合该铁矿的实际生产情况，获得满足该矿山最优采场参数值为：分段高度14m、进路间距16m、崩矿步距3m。

［1］乔登攀，汪亮，张宗生．无底柱分段崩落法采场结构参数确定方法研究［J］．采矿技术，2006，6（3）：233－236．

［2］金闯，董振民，贡锁国，等．梅山铁矿无底柱分段崩落法加大结构参数研究［J］．金属矿山，2000（4）：16－19．

［3］黄泽，盛建龙，李迅．无底柱分段崩落法高分段与大间距结构参数分析［J］．采矿技术，2011，11（1）：11－13．

［4］郭雷，熊靓辉．无底柱分段崩落法现状及发展趋势［J］．中国矿山工程，2010，39（6）：44－48．

［5］朱卫东，原丕业，鞠玉忠．无底柱分段崩落法结构参数优化主要途径［J］．金属矿山，2000（9）：12－16．

［6］吴爱祥，武力聪，刘晓辉，等．无底柱分段崩落法结构参数研究［J］．中南大学学报，2012，43（5）：1846－1850．

［7］董鑫，邓红卫．夏甸金矿无底柱分段崩落法采场参数优化［J］．采矿技术，2009，9（3）：4－6．

［8］黄兴益．尖山铁矿无底柱分段崩落法结构参数研究［J］．金属矿山，2012（4）：5－7．

［9］朱焕春．PFC及其在矿山崩落开采研究中的应用［J］．岩石力学与工程学报，2006，25（9）：1927－1931．

［10］刘志娜，梅林芳，宋卫东．基于PFC数值模拟的无底柱采场结构参数优化研究［J］．矿业研究与开发，2008，28（1）：3－5．

［11］程爱平，许梦国，王平．金山店铁矿低贫化放矿数值模拟［J］．金属矿山，2011（1）：31－34．

Study on stope structural parameter optimization of non－pillar sublevel caving in an iron mine

FENG Haonan，SHU Taijing，GUO Jianlai
（Hebei Hanxing Institute of Mine ＆Metallurgy Design Co．，Ltd．，Handan Hebei 056001，China）

Sublevel height，between－access space and caving step space are three important factors affecting sublevel caving．Combined with the production conditions of an iron ore in Jiangxi，using numerical simulation software PFC3D，9different sets of structural parameters of the model are simulated，which are determined by a combination of orthogonal design．The test results are analyzed．It is recommended that the optimal structural parameters of iron mine are parameters with sublevel height 14m，between－access space 16mand caving step space 3m．

non－pillar sublevel caving；orthogonal test；numerical simulation；stope structural parameters；PFC3D

TD853．36

Α

1671－4172（2015）04－0024－04

10．3969/j．issn．1671－4172．2015．04．006

冯浩楠（1978－），男，工程师，采矿工程专业，主要从事矿山设计工作。