基于最小二乘法的高速列车位置估计

王丽娟，陈德旺，贾桂文

WANG Lijuan,CHEN Dewang,JIA Guiwen

北京交通大学 轨道交通控制与安全国家重点实验室，北京100044

State Key Laboratory of Rail Traffic Control and Safety,Beijing Jiaotong University,Beijing 100044,China

1 引言

预计到2020 年，我国的四纵四横铁路客运专线网络总里程将达到16 000 km。客运专线运行时速可以达到300 km/h 或者以上，而客货混跑线路上的客运列车运行时速达到200 km/h 到250 km/h。列车定位是列车运行控制系统的重要组成部分，定位精度的高低对列车的安全和运行效率有着重要的影响[1]。随着列车运行速度的提高，运输密度的进一步加大，列车运行控系统对列车定位精度的要求越高。依照中国列车运行控制系统CTCS 技术规范，查询应答器在200 km/h 及以上的高速铁路中仍然起着列车定位校核的作用[2-5]。

在高速铁路中，列车的每经过一个定位应答器组，列车的位置将进行一次校正[6-9]。列车距离最近相关应答器越远，列车的定位误差越大。定位误差的增大使得列车的行车安全得不到保证，同时也影响了运行效率[10-13]。针对列车定位问题，本文首先建立了高速铁路列车位置计算的数学模型，然后建立了列车位置计算模型，速度平均法模型和最小二乘法模型，最后利用武汉-广州高铁实际运行数据对计算模型进行训练和验证，结果表明使用列车位置计算的最小二乘模型估计的列车位置误差更小，估计结果更可靠。

2 列车位置计算模型

列车位置报告消息包中主要包括位置报告点处的列车速度，报告点的时间和最近相关应答器编号[14-16]，本文提取相关数据建立列车位置计算的数学模型如图1所示，列车的运行方向为应答器1 到应答器2。假设编号为1 和2 的应答器之间有n个位置报告点信息，列车在位置报告点j处的时间和速度分别为tj和Vj，列车在监测点j-1 和j之间的测量走行距离为Dj。

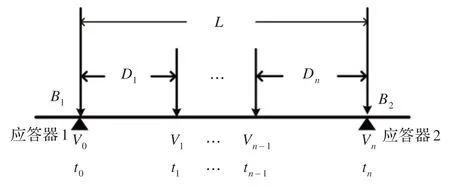
图1 列车位置的计算模型

通过应答器编号1 和2 查询得到应答器的公里标，分别为B1和B2，由此可以得到应答器1 和2 之间的实际距离L为：

由图1 的计算模型可得，车载设备报告的列车在任意位置报告点处的位置为：

其中，m=0 时，P0=B1。

3 两种列车位置估计算法

3.1 速度平均法

由于相邻位置报告点间的时间间隔最长不超过7 s，因此可以认为列车在这一时间段内作匀速、匀加速或者匀减速运动。由此可以应用速度平均法来计算列车在相邻位置报告点间的走行距离。速度平均法可以快速的估算出列车在相邻两应答器之间的位置，具有计算量小的特点。使用这种方法，可以很容易得到列车在应答器1 与应答器2 之间任意相邻两位置报告点间的计算走行距离为：

因此，速度平均法估算的列车在任意监测点处的位置为：

累计列车在相邻应答器间的所有位置报告点的计算走行距离可以得到应答器1 与2 之间的距离为：

3.2 最小二乘法

最小二乘法（Least Square Method）是一种数学优化技术，它以最小化误差的平方和为原则，找到与一组数据相匹配的函数的最佳参数。

列车在相邻两监测点间的走行距离只与两监测点处列车的速度即Vj、Vj-1和运行运行时间Δtj-1,j有关。因此，建立列车在相邻位置报告间的估算模型如下：

其中，[α1,α2]为待求参数。那么，累计n个监测点间的走行距离，则相邻应答器间的距离可表示为：

假设存在N个应答器组间的监测点数据，则列车位置的最小二乘估计模型的优化目标函数为：

其中，Li表示应答器i到i+1 之间的实际距离；表示最小二乘法估计的应答器i到i+1 的距离。由此得到2个未知数，N个方程的方程组，运用最小二乘法计算出模型参数[α1,α2]。

4 结果分析

本文使用的的数据来源于武汉-广州高铁中咸宁北到乌龙泉东的实际运营数据。文中使用的数据包括133个列车位置报告点信息，其中包含39 个应答器位置信息，从而构成了132 组位置报告间信息和38 组应答器间距离信息。根据训练集数据应多于验证集数据的原则，本文将应答器组数据中的25 组应答器间信息，87 组位置报告间信息作为训练集，剩余13 组应答器间信息，45组位置报告间信息作为验证集。

为了更好地比较列车位置计算算法，本文定义了3个评价指标来进行说明：误差百分比（Percentage Error）、误差均值（Mean Error）以及均方根误差（Root Mean Square Error）。这3 个指标用来评价列车位置估计模型与算法的有效性，计算公式分别如式（9）、（10）、（11）所示：

其中，ΔLi表示应答器i与i+1 之间的实际距离与算法模型估算的距离之差。

在相同的实验环境下，采用速度平均法和最小二乘法数据进行实验，计算得到[α1,α2]=[0.464 6,0.510 2]，训练集各项评价指标结果如表1 所示。表1 的数据表明最小二乘模型较好的拟合了训练集的数据并且定位误差减少了64%。40 组应答器间误差如图2 所示。

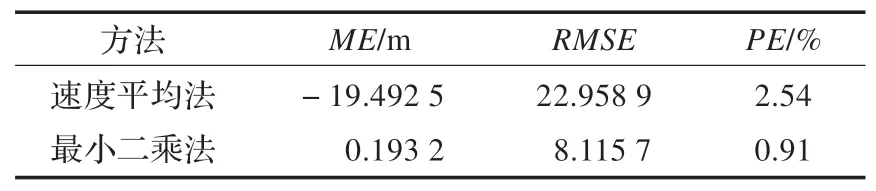
表1 训练集各项评价指标

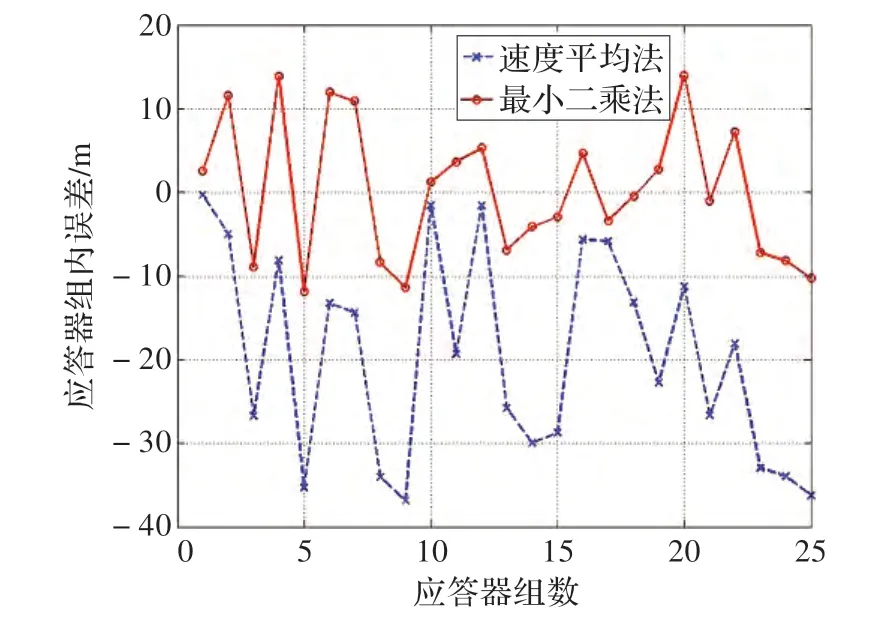
图2 训练集各应答器间误差图

将训练得到的最小二乘模型应用到验证集中得到验证集的各项指标，如表2 所示。从表中可以看到最小二乘模型平均误差上优于速度平均法很多，进一步的说明了最小二乘模型的无偏性，而平稳性方面也比速度平均法好很多。在决定方法的优劣性的指标误差百分比上，最小二乘法定位误差减少了63.8%。35 组验证集应答器间误差如图3 所示。

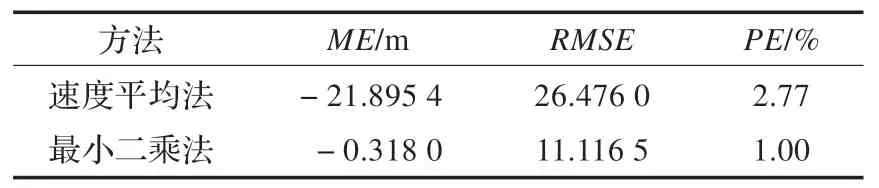
表2 验证集各项评价指标

图3 验证集各应答器间误差图

5 结论

精确的列车定位对于保障列车的安全有着重大的意义，也有助于提高列车的通过能力以及提高铁路网的运行效率。本文首先建立了列车位置计算的数学模型，然后利用速度平均模型和最小二乘模型对列车位置进行估计和分析，结果表明最小二乘模型估计的列车的位置精度比速度平均模型高，最小二乘模型具有简单、计算量小的特点，适用于工程中使用，但仍需在实际中加以验证和改进。

[1] 钱立新.世界高速铁路的发展水平和中国高速铁路的技术进展[J].铁路采购与物流，2009（10）：19-21.

[2] 李秀明，杜赟睿.中国高铁发展分析[J].科技致富向导，2010（5）：34-35.

[3] 徐俊岐.高速铁路应答器运用分析与探索[J].科技资讯，2011（17）：20-52.

[4] 闫剑平，步兵.高速铁路列车定位技术的研究[J].北方交通大学学报，1999，23（5）：73-76.

[5] CTCS-3级列控系统与GSM-R接口规范V1.0[S].2009-08-09.

[6] Kurt W.High speed railway：U S，2，228，800[P].1941-01-14.

[7] Cheng Tao，Qiu Jiahui，Chen Houjin，et al.Position-based modeling for wireless channel on high-speed railway under a viaduct at 2.35 GHz[J].IEEE Journal on Selected Areas in Communications，2012，30（4）：834-845.

[8] 周儒，钱路路，孙中东，等.查询应答器原理及其应用[J].铁道通信信号，1995，31（12）：3-6.

[9] 李向红，李永善，曹进.高速铁路中的查询应答器[J].铁路通信信号，2004，40（10）：5-7.

[10] 胡东源.GSM-R/CTCS 在中国铁路的应用与发展战略[J].铁道通信信号，2003（1）：7-l1.

[11] Uhlirz M.Concept of a GSM-based communication system for high-speed trains[C]//Proceedings of IEEE 44th Vehicular Technology Conference，1994.

[12] Kastell K.Improvments in railway communication via GSM-R[C]//Proceedings of Vehicular Technology Conference（VTC 2006），2006.

[13] Zeng Jing，Wu Pingbo.Stability analysis of high speed railway vehicles[J].JSME International Journal Series C，2004，47（2）：464-470.

[14] Xia He，Zhang Nan，De Roeck G.Dynamic analysis of high speed railway bridge under articulated trains[J].Computers & Structures，2003，81：2467-2478.

[15] Dhahbi S.Study of the high-speed trains positioning system：European signaling system ERTMS/ETCS[C]//Proceedings of 4th International Conference on Ogistics（LOGISTIQUA），2011.

[16] Guo Hu，Zhu Wenfa.Train positioning based on strap-down inertial system[C]//Proceedings of IEEE Eleventh International Symposium on Autonomous Decentralized Systems（ISADS），2013.