基于灰度-梯度二维对称Tsallis交叉熵的阈值分割

朱 磊，吉 峰，白瑞林

ZHU Lei1,JI Feng2,BAI Ruilin1

1.江南大学 轻工过程先进控制教育部重点实验室 信息与控制实验教学中心，江苏 无锡214122

2.无锡信捷电气股份有限公司，江苏 无锡214072

1.Information and Control Experiment Teaching Center, Key Laboratory of Advanced Process Control for Light Industry（Ministry of Education）,Jiangnan University,Wuxi,Jiangsu 214122,China

2.Xinje Electronic Co.,Ltd.,Wuxi,Jiangsu 214072,China

1 引言

图像分割是机器视觉检测系统的前期处理技术，其目的是从复杂的背景中分离出感兴趣的目标区域，以便后续目标识别。其中，阈值分割是一类简单实用的图像分割方法。根据分割的空间特性，可以把阈值分割分为全局阈值和局部阈值两大类。全局阈值分割法因其实现简单、实时性较高等特点，得到了广泛的应用[1-2]。基于信息熵概念（例如最大熵[3]、最小交叉熵[4]、Tsallis 熵等）的阈值分割法是近来研究的热点。Albuquerque 等[5]首先利用Tsallis 熵的非广延性，提出带有调节参数的一维Tsallis 熵阈值分割法，该方法具有较强的普适性且比传统最大熵更为有效。唐英干等[6]把最小交叉熵与Tsallis 熵相结合，同时考虑目标和背景之间的信息量差异和相关性信息，提出一维最小Tsallis 交叉熵阈值分割法，取得了良好的分割效果。但是基于一维直方图的方法对背景复杂或者噪声较强的图像分割效果往往较差，因此研究人员开始不仅考虑像素点的灰度信息还考虑像素点邻域的均值、中值等信息，即通过二维直方图搜寻最佳阈值。Sahoo 等[7]将一维Tsallis 熵阈值分割法拓展到灰度级-平均灰度级二维直方图上，利用图像的邻域空间信息，提高了算法的分割效果，但是二维运算量呈指数上升，难以满足实时性。为了解决这一问题，朱炜等[8]提出基于粒子群优化算法的二维Tsallis 熵阈值分割法。吴一全等[9]则提出基于斜分策略的二维Tsallis 熵阈值分割法，采用与主对角线垂直的斜线按灰度级与平均灰度级之和大小来进行分割，提高了分割效果，并引入递推算法加快了运算速度，但此斜分法普遍性不强[10]。唐英干等[11]不仅考虑像素之间的空间邻域信息，而且考虑了目标和背景之间的相互关系，提出二维Tsallis 交叉熵阈值分割法，并采用粒子群优化算法寻找最佳阈值，大大提高了算法的分割效果和实时性。

然而，二维Tsallis 交叉熵阈值分割法存在着如下不足之处：（1）通过灰度级-平均灰度级直方图来计算最佳阈值，只考虑了沿主对角线的两个区域，忽略了其他两个区域应予考虑的目标点和背景点，势必影响分割效果，甚至造成错分；（2）基本粒子群算法搜寻最佳阈值存在后期收敛速度慢和精度低等特点，并且在迭代计算适应度函数时存在着大量冗余计算，因此运行效率仍有待进一步提高。对于第一个问题可以引入其他变量构建二维直方图，尽可能多地考虑所有的目标点和背景点，提高图像分割的效果；对于第二个问题可以采用搜索精度更高和速度更快的优化算法，并在计算适应度函数时采用某种快速运算方法，以其降低计算的复杂度。

基于以上考虑，引入梯度变量构建新的二维直方图，并在一维对称Tsallis 交叉熵的基础上导出二维对称Tsallis 交叉熵阈值选取公式。采用新的灰度-梯度二维直方图，充分考虑像素之间的邻域梯度信息，摒弃传统二维直方图的近似假设，使图像分割更为准确，同时缩小遍历的解空间，提高算法的运行效率。另外，采用基于tent 映射的混沌小生境粒子群优化算法搜寻二维最佳阈值向量，克服基本粒子群算法的缺陷，并在计算适应度函数时引入快速递推算法，进一步提高了算法的实时性。

2 基于灰度-梯度二维对称Tsallis交叉熵的阈值分割

2.1 灰度-梯度二维直方图

设一幅大小为M×N图像的灰度级f(x,y)取0,1,…,L-1，采用8邻域模板滤波得到平均灰度级g(x,y)。传统的二维直方图都是由灰度级f(x,y)和平均灰度级g(x,y)构建而成。如图1（a）所示，主对角线区域0 和区域1 分别对应目标点和背景点；而区域2 和区域3 对应边缘点及噪声点。基于该传统直方图的二维Tsallis 交叉熵阈值分割法假设二维直方图中远离主对角线的分量近似为0，即忽略区域2 和3 这两个部分的目标点和背景点。这样的二维直方图必然会丢失少量或者部分目标点和背景点。若采用灰度-梯度直方图及其区域划分方式可以弥补这一缺陷，提高分割阈值的准确性。如图1（b）所示，横坐标为像素的灰度级与平均灰度级的均值，即为[f(x,y)+g(x,y)]/2，纵坐标则取该像素的邻域梯度，这里用像素灰度级和平均灰度级的绝对差|f(x,y)-g(x,y)|表示。可见，这种二维直方图既对噪声图像有平滑作用，又可以使图像边缘及细节分割的更加准确。若用h(i,j)表示该二元组([f(x,y)+g(x,y)]/2=i,|f(x,y)-g(x,y)=j|)出现的频数，则发生的联合概率为：

图1 传统与灰度-梯度二维直方图

{p(i,j)}即为灰度-梯度二维直方图。这里M×N为图像的总像素点数；i=0,1,…,H；j=0,1,…,W，H和W分别为最大的平均值和最大邻域梯度。

若(t,s)是待选取的阈值向量，(t,s)把灰度-梯度二维直方图划分为四部分，如图1（b）所示。区域0 和区域1 的邻域梯度较小，即灰度级与平均灰度级相近，因此分别对应目标点和背景点；区域2 和区域3 的邻域梯度较大，即灰度级与平均灰度级相差较大，因此对应边缘点及噪声点。如图1（c）所示，为Lena 图像的灰度-梯度二维直方图，在区域0 和1 存在联合概率高峰，因目标点和背景点的邻域梯度较小，数量在图像中占较大比例；区域2 和3 则存在联合概率低谷，因边缘点和噪声点的邻域梯度较大，数量在图像中占较小比例。可见，这种新的灰度-梯度二维直方图比传统直方图更加全面地考虑了背景类和目标类的内部点，可以提高分割的效果，而邻域梯度的最大值W往往远小于最大灰度级L-1，所以遍历的解空间大大缩减，可以进一步提高了算法的运行效率。

2.2 对称Tsallis交叉熵的阈值分割

将新的灰度-梯度直方图运用到对称Tsallis 交叉熵阈值选取中，导出算法的相关计算公式。设(t,s)为灰度和梯度构成的阈值向量，二维直方图1（b）中区域0（目标类）和区域1（背景类）的概率分别为po(t,s) 和pb(t,s)，则

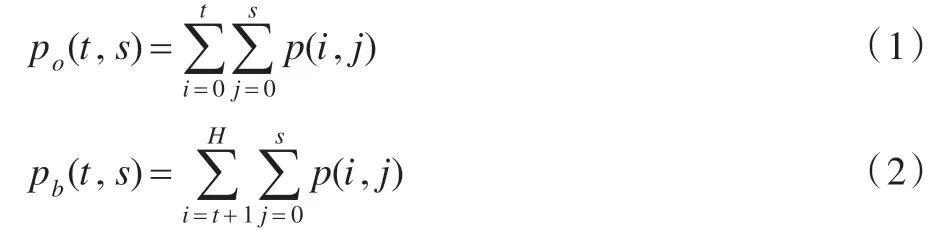
式中，t为灰度（均值）分割阈值，s为邻域梯度分割阈值，且0 ≤t≤H，0 ≤s≤W。区域0 和区域1 的均值向量μo(t,s)和μb(t,s)分别为：

将文献[12]中一维对称Tsallis 交叉熵的准则函数推广到二维，则基于灰度-梯度直方图的二维对称Tsallis交叉熵的阈值选取准则函数Φ(t,s)为：

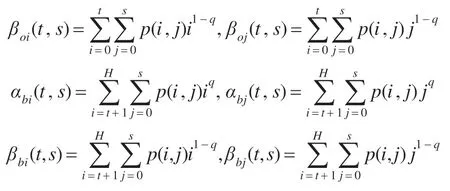
其中参数q通常取0.8 最佳，准则函数Φ(t,s)越小，分割前后图像之间的差异性就越小。当二维对称Tsallis 交叉熵达到最小时，取得最佳阈值向量(t*,s*)，即

基于灰度-梯度直方图的二维对称Tsallis 交叉熵阈值分割法求解二维最佳阈值向量，其优点在于不仅考虑了目标和背景之间的信息量差异，使分割前后图像之间的误差最小，而且考虑了相关性信息，使类内灰度更加均匀，因此提高了分割的准确性。但是从上面准则函数公式Φ(t,s)可以看出，该方法和基于传统二维直方图的Tsallis 交叉熵阈值分割法同样具有较高的计算复杂度。因此，本文引入快速递推算法对其相关量进行计算，以此减少其运算量。

从上述公式（5）、（7）以及（8）可知，实际需要计算的相关量为以及。由于涉及的相关量较多，在此以po(t,s)和αoi(t,s)两个量为例给出快速递推计算公式。

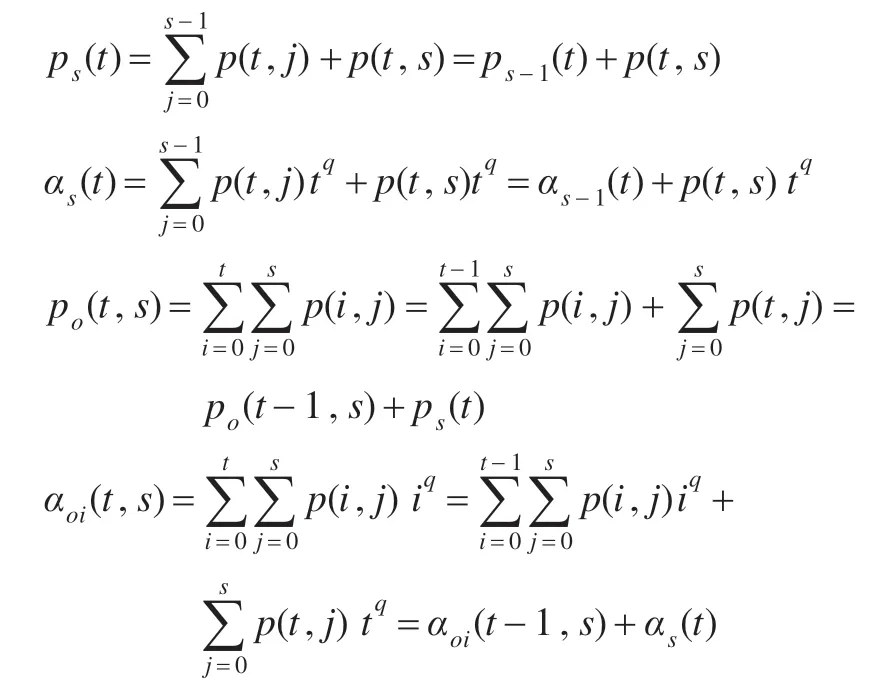
对于每次计算po(t,s)和αoi(t,s)两个量可以利用前面已经得到的po(t-1,s)和αoi(t-1,s)以及当前的ps(t)和αs(t)，而ps(t)和αs(t)是通过计算每一列值累加算出，总共H+1 列，不用每次重新逐点计算。类似地，可以递推计算以及。通过这样的快速递推计算，可以降低目标准则函数的计算复杂度，提高了算法的运行效率。

3 对称Tsallis 交叉熵的阈值分割的混沌小生境粒子群优化算法

粒子群算法是模拟鸟集群飞行觅食行为的群智能演化方法，它能够以较大概率搜索到目标函数的全局最优解。设在n维搜索空间中，向量Xi=(xi1,xi2,…,xin)表示为第i个粒子位置，向量Vi=(vi1,vi2,…,vin)表示为第i个粒子速度。对称Tsallis 交叉熵准则函数Φ(t,s)作为评价粒子优劣的适应度函数，迭代搜索整个解空间。在迭代搜索过程中，粒子通过两个最优解更新当前的位置和速度，设Pi(k)为粒子i的历史最优解，Pg(k)为当前粒子群的全局最优解。基本粒子群算法的位置和速度迭代公式如下：

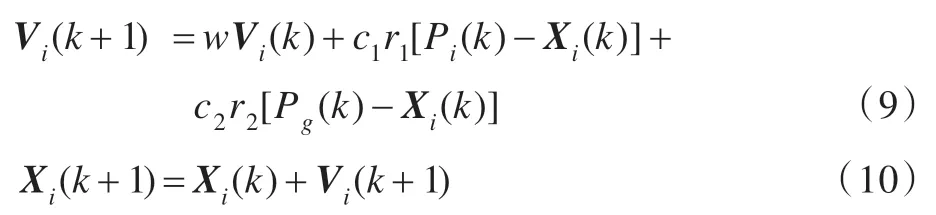
其中，k为迭代次数；c1和c2为学习因子，一般取c1=c2=2；r1和r2为（0，1）上的随机数；w为惯性因子，它对粒子的全局和局部搜索能力有着较大的影响，因此本文采用线性递减方式来调节惯性因子：

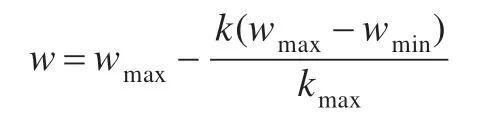
其中，kmax为最大迭代次数，设最大惯性因子wmax=0.95，最小惯性因子wmin=0.40，迭代时粒子速率取值范围为[Vmin,Vmax]，Vmin=Vmax=10。

上述基本粒子群算法虽简单，但是容易陷入局部最优解，难以保证收敛到全局最优解。此外基本粒子群算法还存在着后期搜索精度低和收敛速度慢等缺陷。为了弥补基本粒子群算法这一缺陷，结合小生境进化策略与混沌变异的随机性和遍历性，以提高搜索的精度以及速度。小生境进化策略是把粒子群分为几个子种群，通过子种群之间的欧式距离来控制其竞争，形成各个子种群局部极值同步搜索，避免粒子的早熟；同时在搜索过程中引入混沌变异，使粒子快速跳出局部极值。由于tent 映射具有相对较高的寻优效率，因此本文采用基于tent映射的混沌小生境粒子群优化算法搜寻二维最佳阈值向量。tent映射方程表示为：

由于上述tent 映射存在小周期点和不稳定点的不足，当达到小周期点(0.2,0.4,0.6,0.8) 或者不稳定点(0,0.25,0.50,0.75)时，再次采用如下扰动方程：

其中，λ为收缩因子，e为粒子群的进化代数，u为控制收缩速度，一般取2。

基于tent 映射的混沌小生境粒子群优化算法搜寻二维最佳阈值向量步骤如下：

步骤1初始化混沌小生境粒子种群。随机产生K个粒子（本文取12），并把这些粒子分成C（本文取4）个子种群，粒子位置是像素灰度和梯度构成的向量，粒子速度在[Vmin,Vmax]范围内随机产生。

步骤2根据式（5）计算每个粒子的适应度函数值，该适应度函数值由快速递推算法计算得到，然后找出每个小生境种群中的最优粒子和全局最优粒子。

步骤3计算两个子种群最优个体之间的欧式距离D。当D＜R（R为小生境半径，本文取）时，对小生境最优个体的适应度函数值低者置零，并对置零和最劣粒子重新初始化，直至任意两个小生境最优个体之间的距离D≥R。

步骤4按式（11）至（13）对所有小生境最优个体进行tent映射的混沌迭代变异，重新计算其适应度函数值，若大于原适应度函数值，则更新当前最优个体的位置。

步骤5按式（9）和式（10）更新每个粒子的位置和速度。

步骤6当达到最大迭代次数，得到最佳阈值进行图像分割；否则返回步骤2。

4 实验结果及分析

为了验证算法的有效性，本文针对大量各种典型图像进行了仿真实验，并将本文方法分别与基于灰度级-平均灰度级直方图的二维Tsallis 交叉熵法、二维斜分对称Tsallis交叉熵法[12]以及最近提出的二维Otsu 准分法[14]在分割效果和运行时间上进行对比。这里，算法的硬件运行环境为Intel Pentium®CPU E6700 3.2 GHz，2 GB内存，软件编程语言为Matlab2011b。

选取五幅图像加以说明，这五幅图像分别为米粒图像（257×257）、辣椒图像（200×200）、建筑图像（600×600）、火焰图像（309×226）以及红外图像（210×192）。如图2～6所示，从上至下依次是原始图像、文献[11]的分割结果、文献[12]的分割结果、[14]的分割结果以及本文方法的分割结果。相应的分割阈值向量和运行时间见表1。

图2 原始图像

图3 文献[11]分割结果

图4 文献[12]分割结果

图5 文献[14]分割结果

图6 本文分割结果

（1）图像分割效果对比。对于背景光照不均匀的多目标米粒图像，二维Tsallis 交叉熵法和二维Otsu 准分法虽然较为准确地分割出了下半部分目标，但是在上半部分都存在着严重的错分，抗噪性能较差，从而无法识别米粒目标，二维斜分对称Tsallis 交叉熵法却丢失了下方米粒目标，而本文方法准确得分割出了各个米粒，分割效果较好；对于背景较为复杂的辣椒图像，二维Tsallis交叉熵法和二维斜分对称Tsallis 交叉熵法分割出了较大的辣椒目标，但是局部较小辣椒目标分割效果不佳，二维Otsu 准分法优于上述方法，但是前景中的较大辣椒目标边缘分割不够准确，而本文方法对辣椒边缘分割更加准确，特别是对局部小目标的辣椒；对于灰度分布不均匀的建筑图像，二维Tsallis 交叉熵法分割效果不好，在墙壁上产生了大面积的错分，二维Otsu 准分法效果有所改善，但是在图像上方产生阴影，同时图像右侧的墙壁并未有效地分割出来，而二维斜分对称Tsallis 交叉熵法和本文方法比较准确地分割出了房屋的边界，不足之处在于瓦片纹理未能分割出来；对于模糊的火焰图像，二维Tsallis 交叉熵法丢失了左上方火焰目标，且对火焰的边缘分割不够准确，二维斜分对称Tsallis 交叉熵法和二维Otsu 准分法分割效果相对较为优秀，而本文方法对火焰的分割更为精确；对于红外小目标图像，二维Tsallis交叉熵法和二维斜分对称Tsallis 交叉熵法均未能准确提取出图像中的人物，存在大量的误分现象，二维Otsu准分法分割效果较差，产生大面积阴影部分，而本文方法十分准确地提取出了三个人物目标，分割效果良好。从上述实验得出，本文方法在分割性能上有着明显的优势，尤其是对米粒、红外等这样的小目标图像。

（2）运行时间对比。在本文测试中，基于灰度级-平均灰度级直方图的二维Tsallis 交叉熵法采用粒子群算法搜寻二维最佳阈值向量，其迭代次数为50 次，而经过多次运行，本文基于tent 映射的混沌小生境粒子群优化算法仅需迭代20 次就可以搜寻到全局最优解。由表1可以看出，本文方法的运行时间比基于传统直方图的二维Tsallis 交叉熵法运行时间提高了30 倍，比二维斜分对称Tsallis 交叉熵法快了1 倍左右，比二维Otsu 准分法快了至少40%以上。可见本文方法在实时性方面有很明显的优势。这是因为：（1）在灰度-梯度二维直方图中，邻域梯度的最大值与最大灰度级相比很小，大大缩减了解空间的搜索范围；（2）采用了混沌小生境粒子群优化算法，提高了阈值搜索的速度。同时，快速递推算法在迭代计算适应度函数中降低了计算的复杂度，使得算法的实时性进一步提高。

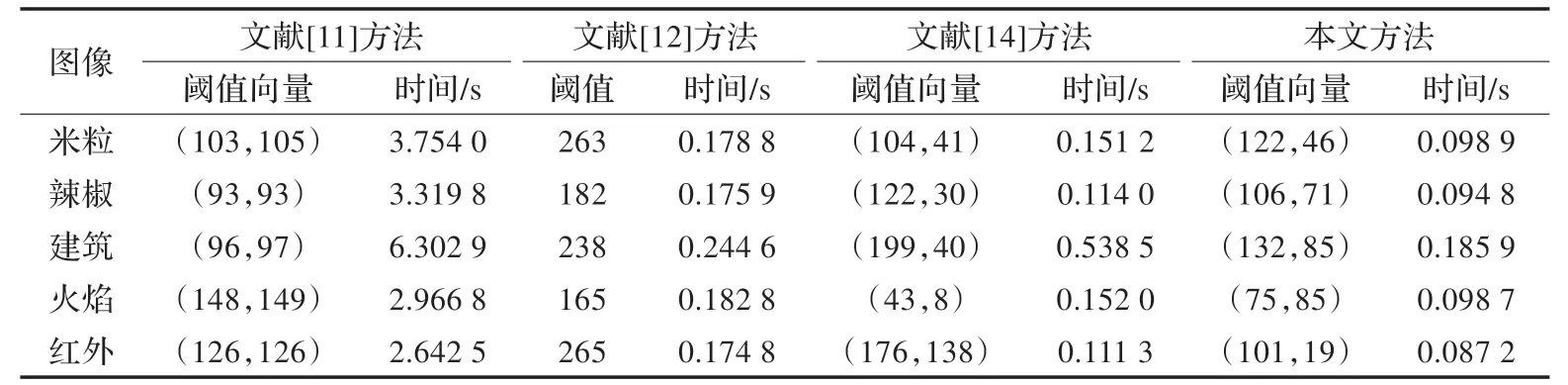
表1 四种算法的阈值向量和运行时间

（3）图像分割质量评价。本文采用均匀性测度作为衡量图像分割结果的性能评价标准。在阈值分割中，均匀性测度是衡量两个区域内部的均匀性程度，其大小在一定程度上反映了阈值分割方法的优劣，认为测度越大，分割效果越好。基于灰度级-平均灰度级的二维Tsallis 交叉熵法和二维Otsu 准分法的二维阈值向量采用向量中较小的一个作为关键阈值，对其进行均匀性测度的计算，而本文灰度-梯度二维对称Tsallis 交叉熵阈值分割法采用阈值向量中的第一个为关键阈值。四种算法相应的均匀性测度位于表2，在表中可以看出从评价准则角度可以得出本文方法优于其他三种方法，同时也说明了该方法使得类内的灰度更加均匀。

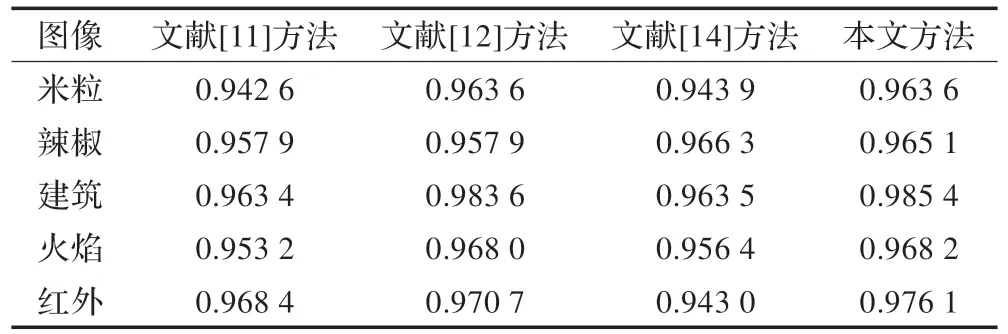
表2 四种算法的均匀性测度

5 结论

本文提出的基于灰度-梯度二维对称Tsallis 交叉熵的阈值分割法充分利用了邻域像素的灰度信息，也考虑了与边缘轮廓相关的邻域梯度信息，在一定程度上弥补了传统灰度级-平均灰度级直方图的近似错分问题，并且通过混沌小生境粒子群优化算法在迭代计算适应度函数值时，引入快速递推算法，提高了实时性。仿真结果表明，本文方法不仅提升了算法的实际分割效果，而且提高了算法的运行效率，因此该方法具有较高的实用价值。此外，本文方法还可以推广到其他二维阈值分割方法中中去。为了进一步满足实际应用，实现对非均匀光照、灰度分布不均匀图像的有效分割还可以将该方法引入到局部阈值法中，这是下一步的研究工作。

[1] 张新明，党留群，郑延斌，等.一种改进的二维最小交叉熵图像分割方法[J].光电工程，2010，37（11）：103-109.

[2] Fan Jiulun，Lei Bo.A modified valley-emphasis method for automatic thresholding[J].Pattern Recognition Letters，2012，33（6）：703-708.

[3] Kapur J N，Sahoo P K，Wong A K C.A new method for gray-level picture thresholding using the entropy of the histogram[J].Computer Vision，Graphics，and Image Process，1985，29（3）：273-285.

[4] Brink A D，Pendock N E.Minimum cross-entropy thresold selection[J].Pattern Recognition，1996，29（1）：179-188.

[5] Portes De Albuquerque M，Esquef I A，Gesualdi Mello A R.Image thresholding using Tsallis entropy[J].Pattern Recognition Letters，2004，25（9）：1059-1065.

[6] 唐英干，邸秋艳，关新平，等.基于最小Tsallis交叉熵阈值图像分割方法[J].仪器仪表学报，2008，29（9）：1868-1872.

[7] Sahoo P K，Arora G.Image thresholding using two-dimensional Tsallis-Havrda-Charvát entropy[J].Pattern Recognition Letters，2006，27（6）：520-528.

[8] 朱炜，徐玉如，秦再白.一种新的基于二维Tsallis 熵的阈值分割方法[J].计算机工程与应用，2007，43（27）：54-58.

[9] 吴一全，潘喆，吴文怡.二维直方图斜分Tsallis-Havrda-Charvát熵图像阈值分割[J].光电工程，2008，35（7）：53-58.

[10] 吴一全，张金矿.二维直方图θ-划分Tsallis 熵阈值分割算法[J].信号处理，2010，26（8）：1162-1168.

[11] 唐英干，邸秋艳，赵立兴，等.基于二维最小Tsallis 交叉熵的图像阈值分割方法[J].物理学报，2009，58（1）：9-15.

[12] 吴一全，沈毅，刚铁，等.基于二维对称Tsallis交叉熵的小目标图像阈值分割[J].仪器仪表学报，2011，32（10）：2161-2167.

[13] 贾东立，张家树.基于混沌变异的小生境粒子群算法[J].控制与决策，2007，22（1）：117-120.

[14] 张新明，孙印杰，郑延斌.二维直方图准分的Otsu 图像分割及其快速实现[J].电子学报，2011，39（8）：1778-1784.