FPGA 的高性能暗原色先验算法设计

蒋守欢，汪荣贵，王 晶，张冬梅，李 想

JIANG Shouhuan,WANG Ronggui,WANG Jing,ZHANG Dongmei,LI Xiang

合肥工业大学 计算机与信息学院，合肥230009

School of Computer and Information,Hefei University of Technology,Hefei 230009,China

1 引言

雾天退化图像的处理一直以来是图像增强研究的热点，特别是近几年北京等地区出现雾霾，严重影响了户外交通的安全。近年来，He 等[1]提出地暗原色先验去雾算法，对雾天图像有很好的处理效果。该算法基于一个先验规律，即大多数户外无雾图像的局部区域的R、G、B三个通道中，至少存在一个通道的值很低几乎为零，该值称为暗原色值。由暗原色值可以初步估计出透射率，接着用软抠图的方法进一步对透射率求精，得到恢复后的图像。该算法使用软抠图来细化透射率，耗费了大量的运行时间和资源，不满足实际的应用。

针对上述问题，研究人员提出了一些基于暗原色先验的改进算法，其中杨靖宇等[2]用内插值的方法对透射率求精，但这种方法仅针对航空影像特有的环境进行处理；很多学者用双边滤波对透射率进行处理[3-9]，但是双边滤波的二维实现方式和浮点型空间临近度因子不利于硬件实现，且计算量大，实时性难以得到满足。引导滤波[10]是He 等提出来的一种新型滤波算法，主要应用在图像平滑和图像细节增强。引导滤波在图像平滑时，具有较好的保边去噪的效果。本文用引导滤波器对透射率求精[10]，采用自顶向下[11-15]的设计方式，把暗原色先验算法划分为两个模块：透射率模块和引导滤波器模块，其中引导滤波器模块是设计的重点，它的核心模块是均值滤波，通过保存局部窗口最左边与最右边两列的值，加上/减去其相应列中某个像素的点的值，设计出了一种资源占有率低、延迟低的均值滤波器。与传统的均值滤波相比，文中提出的快速算法可以消除很多冗余的计算，能有效地降低计算复杂度，达到每个时钟周期处理一个像素，模块的设计具有并行流水的特点，适合FPGA的设计方式，有效提高了系统的性能。用Altera 公司CycloneII 系列的EP2C70 的FPGA 开发板实现提出的快速算法。综合实验结果表明，快速暗原色先验算法的逻辑资源使用量和内存资源使用量较低，低端FPGA 可满足要求，系统最大运行频率可达107 MHz。另一方面，把FPGA 实现的快速方法处理结果与Matlab 结果作比较，最大误差率不大于0.8%，并且每秒可以处理1 024×1 024 大小图像100 帧，完全满足实时性要求。

2 暗原色先验算法

2.1 暗原色先验模型

大气散射模型[10]是由McCartney 首次提出，该模型描述了雾天图像的退化过程，可用如下公式表示：

I表示观测图像，J是需要恢复的图像，A为全球大气光，t为透射率，去雾的目标就是从I中恢复J。

暗原色先验理论是He 等对大量户外无雾图像做统计试验得到的，该理论认为在大多数非天空的局部区域内，总是存在某些像素点，其R、G、B三个通道中至少有一个通道的像素值趋近于0，即：

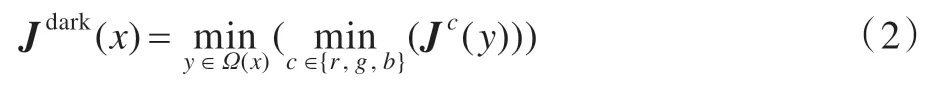
Jc即像素J的某一颜色通道，Ω(x)是以像素x为中心的一块方形区域，Jdark是图像J在Ω(x)区域内的暗原色。

在公式（1）中，首先假设A 为常量，t在一个局部区域内的值为固定值～t，那么对公式（1）两次取最小值运算，为使还原后的图像更有真实感和深度感，引入一个常量ω，表达如下：

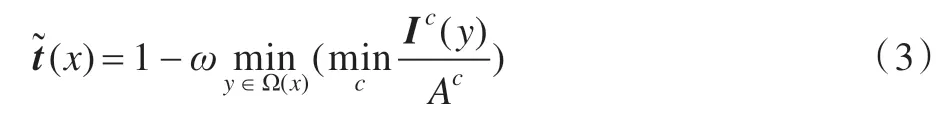
最后由下式计算去雾后的清晰图像：

2.2 引导滤波器对透射率求精

由于基于暗原色先验假设求出的透射图存在伪影或者块状效应，因此采用引导滤波器对透射图作进一步处理。

图像引导滤波是一个线性平移可变的滤波过程，基本思想为：引导图像与平滑后的图像之间存在局部线性的关系，设引导图像为I，输入图像为p，则输出图像q为：

其中ak、bk为线性系数，且在局部窗口wk中为常数；Ii为引导图像中的一个像素点；qi为输出图像中的一个像素点。为确定以上公式中的线性系数，并满足使得q与p的差别最小，可将该系数的确定转化为最优化问题进行求解：

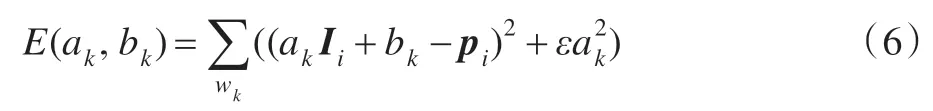
其中ε为防止ak取值过大的调整参数，则ak、bk求解表达式为：

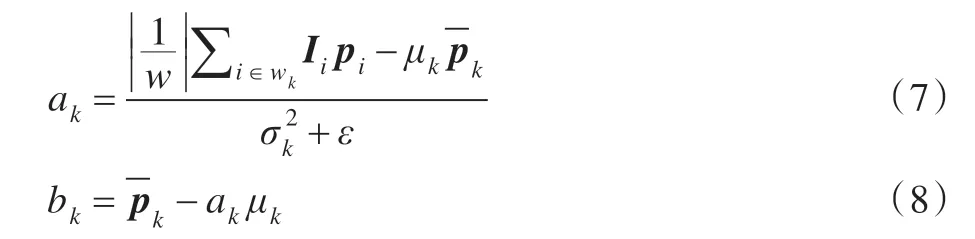
其中μk和分别表示引导图像I中局部窗口wk的均值和方差；|w|表示局部窗口wk的像素个数；表示输入图像p在局部窗口wk的均值。结合公式（7）和（8）得到：

本文选取的引导图像为t，则公式（7）和（8）可以简化为：

最终处理后的透射率图为：

3 引导滤波的快速计算

由2.2 节所述，本文引导滤波图像的选取和待处理的图像是同一幅。其中公式（9）是一个典型的线性变换，其线性变换系数，可由公式（7）和（8）得出；而公式（10）、（11）需计算每个窗口内的均值和方差，由方差公式可得：

3.1 传统均值滤波计算方法

传统的均值滤波计算方法是对每一个新的像素点计算其邻域内(2W+1)×(2W+1)个像素点的和。这样每一次的计算复杂度为Ο((2W+1)2)，对于大小为M×N的图像，其复杂度为Ο(MN(2W+1)2)，若图像窗口(2W+1)较大，不仅使得计算复杂度增加，同时不符合FPGA 的并行流水的处理方式，会耗费很大的逻辑资源，降低系统的最大运行频率，不利于硬件的实现。

3.2 改进的均值滤波计算方法

针对传统均值滤波计算复杂度高的问题，本文设计一种与计算复杂度和窗口大小无关的均值滤波器，优化后的滤波器其时间复杂度不依赖于窗口的大小，节省资源的同时，提高了系统的频率。

一幅图像I中，I(x,y)表示像素点(x,y)的亮度值，定义SUM(x,y)表示以(x,y)为中心(2W+1)2个像素点的和，SUM(x,y)表示第x列，行坐标范围为[y-W,y+W]共2W+1 个像素点的和，mean(x,y)表示以(x,y)为中心(2W+1)2个像素点的均值。图1（1）为SUM(x-1,y)，图1（2）为SUM(x,y)，二者的区别是图1（2）所示的标记为“ + ”和“ - ”的部分。其中：

（1）SUM(x+W,y)通过标记为“ + ”的2W+1 个像素计算；

（2）SUM(x-W-1,y) 通过标记为“ - ”的2W+1个像素计算。

SUM(x,y)和mean(x,y)可通过下式求得：

图1（2）中，标记为“-”的且有阴影线部分共2W个像素的和存储在sum buffer 中，这个和的计算可以通过SUM(x-W-1,y)减去左上角标记为“ - ”的亮度值I(x-W-1,y-W)得到。通过这种方法，SUM(x,y)的时间复杂度降低为O(2W+1)。

当一行中所有的像素都计算完成，此时要产生下一行以(x,y+1)为中心，(2W+1)2个像素的和SUM(x,y+1)，如图1（3）所示。SUM(x,y+1)的计算同样可以使用上述所描述的方法。回顾在计算SUM(x+2W+1,y)时，由于阴影部分带有“+”标注的和已经存储到sum buffer中，通过读取阴影部分的sum buffer，加上I(x+W,y+W+1)，就能得到SUM(x+W,y+1)。同理SUM(x-W-1,y+1)可由计算SUM(x-2W-1,y+1)时，存储在sum buffer的值加上左上角“- ”标注像素得到。

图1 改进的均值滤波器方法

图2 窗口的扫描方式

综上且由公式（14），把得到的SUM(x-W-1,y+1)和SUM(x+W,y+1)存储到temporal sum buffer 中，分别用来计算SUM(x,y+1)和SUM(x+2W+1,y+1)，如图1（4）所示。通过这种优化，算法的时间复杂度为常数，与窗口的大小无关。

上述方法中，为了计算所有的SUM(x,y)，需要扩大扫描范围得到对应的SUM(x+W,y)和SUM(x-W-1,y)。如图2（1），当扫描窗口进入图像第一个点的时候，虽然这时的I(-W,-W) 超出图像范围，仍需要计算SUM(0,-W)。图2（2）中随着窗口沿着x轴移动，超出图像一列时，被访问的I(X,0)用来计算SUM(X,-W)。此时，实际上是I(0,1) 代替了I(X,0)，计算得到的是SUM(0,-W+1)，由于I(X,0)已经超出图像范围，在计算SUM(x-W,-W)时不需要加上SUM(X,-W)的值，SUM(0,-W+1)的值用来计算SUM(-W,-W+1)。图2（3）为两个不同窗口交替进行处理。当窗口移动到图2（4）时，已经扫描了X×(Y+W)个像素，但是此时仍需要多扫描W个像素如图2（5）所示，即扫描窗口到达图2（6）时共扫描了X×(Y+W)+W个像素。当W远小于Y时，最后的W个像素可忽略，但是在实际应用中一般不忽略。

4 暗原色先验算法的FPGA 实现

由前文对算法的理论分析，整个算法的流程是先求透射率，然后对透射率求精，最后得出处理结果，因此本文按照自顶向下的设计方式，暗原色先验算法的模块如图3 虚线框内所示。整个算法模块由透射率模块和引导滤波器模块两部分组成，其中透射率模块主要是求暗原色的值，引导滤波器模块主要是均值滤波器的设计。

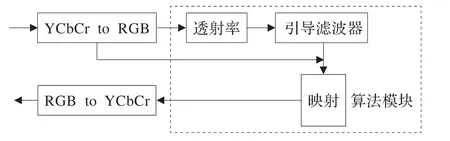
图3 算法模块框图

4.1 透射率t 模块

由公式（2）和公式（3）可知，透射率t的计算首先是求暗原色即局部窗口内3 个通道的最小值，然后由暗原色的值与大气光A 作乘加运算。因此该模块主要的设计是2W+1 行数据的存储(2W+1 表示局部窗口的大小），以及局部窗口内像素的比较。以3×3 窗口为例，设计的投射率模块如图4 所示。

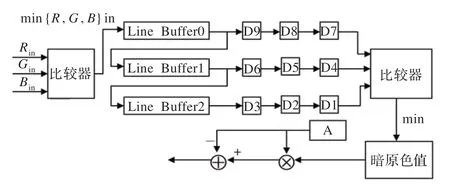
图4 透射率t 的电路结构

其处理流程如下：第一行的数据到来时，先经过空间转换，变换到R、G、B空间，由比较器对3 个通道的数据作比较，得到一个最小值，将其存入Line Buffer0 中；当第二行数据到来时，把Line Buffer0 存储的第一行数据读出，存入到Line Buffer1 中，同时把第二行的数据写入Line Buffer0 中；当第三行的数据到来时，作同样的操作，并将三行的数据进入其后的9 个寄存器中，经过比较器比较，得出暗原色的值。暗原色的值再与大气光A 作乘加运算，求得透射率t。

4.2 引导滤波器模块的实现

由第3 章分析可知，引导滤波器的实现就是要设计4 个均值滤波器，其结构框图如图5 所示。

图5 引导滤波器结构框图

4.2.1 提出的快速均值滤波器实现

在3.2节提出的均值滤波器改进方法，可将滤波器电路设计如图6 所示。假设SUM(x,y)，SUM(x+W,y)，SUM(x-W-1,y)分别存放在寄存b（或b′），bp，bm中。如图2（2）图2（3）所示，当两个不同窗口（当前行和下一行）同时对图像扫描时，寄存器b′用来存放当前行局部窗口中心点超出图像范围，并且局部窗口中心点还未到达下一行图像时局部窗口的和，寄存器b用来存放当前行局部窗口中心点未超出图像范围的局部窗口的和。分别用mask_p，mask_m，reset 清零控制信号来控制bp，bm，b′的清零。假设SUM(x-1,y)已经计算出并且存入寄存器b中，同时可以I(x+W,y+W)与sum buffer 对应位置的值求和，得到的结果为SUM(x+W,y)，存储到寄存器bp中。然后把寄存器b中的值与寄存器bp中的值相加，得到的结果与寄存器bm中的值相减，结果为SUM(x,y)，重新写入寄存器b中。与此同时，把寄存器bp中的值存入temporal sum buffer，延时(2W+1)个时钟周期后转变为寄存器bm的值，用来计算SUM(x+2W+1,y)。把寄存器bm中的值与I(x-W-1,y-W)的差写入sum buffer，为计算下一行的SUM(x-2W+1,y+1)做准备，最后由SUM(x,y)除以局部窗口的像素个数得到均值mean(x,y)。整个设计符合流水线的特征，并且每个时钟周期能计算得到一个SUM(x,y)。

图6 均值滤波器产生单元

4.2.2 引导滤波器电路设计

引导滤波器的处理过程可由公式（9）、（10）、（11）来描述，硬件结构如图7 所示。先通过两个mean filter 得到像素点在窗口内的方差，求出ak、bk，然后经过两个mean filter分别求出其均值，最后经过一个乘加器得到处理结果。

图7 引导滤波器电路结构

4.3 整体电路设计

整个算法流程如图3 所示，结合公式（4），整体电路结构如图8 所示。先通过透射率t模块，得到初步的透射率估计，然后经过引导滤波器对t求精，求精后得到的t～与阈值t0作比较，再与经过fifo 延迟后的原图数据作乘加运算，最后得到输出结果。

图8 所示的整体电路结构，采用全流水线设计，每个时钟周期处理一个像素，从而实现即时输出，另外文中所有用到小数处理的部分均采用扩大整数倍来实现（本文统一采用扩大倍数为512 倍）。整个处理过程的延迟时间由窗口的大小决定。例如，在投射率t模块窗口大小选择为3×3，向导滤波器窗口大小选择为5×5，则整个系统有13 行的延时。

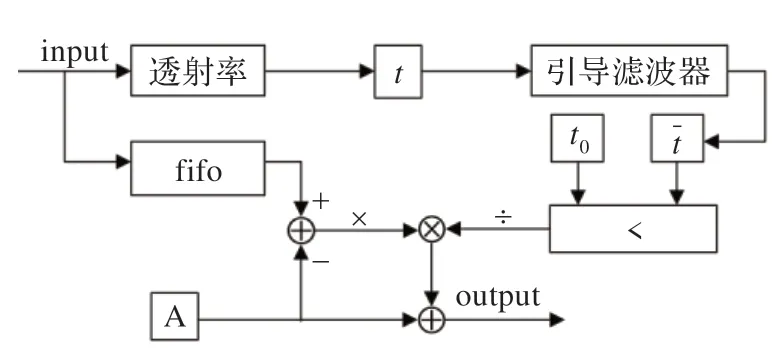
图8 整体电路结构

5 实验结果

本文在Quartus II环境下对改进的暗原色先验算法进行综合，选择Altera 的EP2C70F672I8 芯片，输入图像为8 位，大小为720×576。表1 为选取不同窗口大小时，引导滤波的资源使用量和能达到的最大工作频率。表2给出了暗原色先验算法的处理实验数据，其中引导滤波器选择窗口大小为5×5，局部暗原色窗口大小为7×7。

表1 引导滤波器的资源需求

表2 暗原色先验算法的资源需求

如表1 所示，一方面，随着窗口大小加倍LEs 的使用量基本不变，Memory 的使用量增加，相应的平滑效果也得到提升；另一方面，即使窗口大小加倍，系统最大工作频率仍可达到110 MHz，能够达到实时性需求。

从表2可以看出，整个算法LEs和Memory的使用量不高，系统最高频率可达107 MHz，每个时钟周期处理一个像素，处理速度可达240 f/s，完全满足实时处理的要求。

图9 给出了FPGA 实现的效果。图（a）和图（b）是原始图像，图（c）和图（d）是在FPGA 上实现的暗原色先验算法结果，图（e）和图（f）是在MATLAB 实现的暗原色先验处理结果。从图（c）和图（d）可以看出，经过FPGA 的处理，能够达到去雾的效果，图像细节部分得到明显增强，而且基本上不存在光晕伪影。将（e）、（f）与（c）、（d）的各个像素值作差，绝对值最大为2，则FPGA 处理精度上的误差不大于2/255 ≈0.8%，属于舍去误差，可满足实际处理需求。

图9 实验结果对比图

6 总结

由前文所述，暗原色先验算法理论在图像去雾方面取得了较好的效果，但暗原色先验算法中软抠图部分计算复杂度高，无法满足实际应用需求。文中用引导滤波器代替软抠图，并提出了引导滤波器的快速计算方法，不仅可以实现在软件上的加速，而且在硬件实现上更加符合流水特性，可应用于嵌入式系统的前端，实现各种实时图像处理功能。综合结果表明，在CycloneII系列FPGA上系统最大可运行频率达到107 MHz，每秒能够处理1 024×1 024大小的图像100帧，完全能满足实时性要求。

[1] He Kaiming，Sun Jian，Tang Xiaoou.Single image haze removal using dark channel prior[J].IEEE Trans on PAMI，2011，33（12）：2341-2353.

[2] 杨靖宇，张永生，邹晓亮，等.利用暗原色先验知识实现航空影像快速去雾[J].武汉大学学报，2010，35（11）：1292-1295.

[3] 庞春颖，嵇晓强，孙丽娜，等.一种改进的图像快速去雾新方法[J].光子学报，2013，42（7）：872-877.

[4] Xu Haoran，Guo Jianming，Liu Qing，et al.Fast image dehazing using improved dark channel prior[C]//Proceedings of International Conference on Information Science and Technology（ICIST），Hubei，China，2012.

[5] Sun Kang，Wang Bo，Zheng Zhihui，et al.Fast Single Image Dehazing Using Iterative Biateral Filter[C]//Proceedings of Information Engineering and Computer Science（ICIECS），Wuhan，China，2010.

[6] 蔡超，丁明跃，周成平，等.小波域中的双边滤波[J].电子学报，2004，16（1）：128-131.

[7] 范彦革，刘旭敏，陈婧.各向异性扩散和双边滤波关系的研究[J].微计算机信息，2006（10）：245-247.

[8] Paris S，Durand F.A fast approximation of the bilateral filter using a signal processing approach[C]//Proceedings of European Conference on Computer Vision，Graz，Austria，2006.

[9] Elad M.On the origin of the bilateral filter and ways to improve it[J].IEEE Transactions on Image Processing，2002，11（10）：1141-1151.

[10] He Kaiming，Sun Jian，Tang Xiaoou.Guided image filtering[C]//Proceedings of European Conference on Computer Vision（ECCV），Heraklion，Crete，Greece，2010.

[11] 高清远，李学初.自适应滤波器的FPGA 实现[J].电子测量与仪器学报，2005，19（1）：25-29.

[12] 靖固，刘璐杨，于晓洋.基于FPGA 多变量模糊神经网络控制器设计[J].哈尔滨理工大学学报，2011，16（2）：44-48.

[13] 胡同花，周维龙.基于FPGA的OFDM调制器设计与实现[J].电子设计工程，2011，19（15）：139-141.

[14] 张立，张光新，柴磊，等.FPGA 在多功能计费器系统中的应用[J].仪器仪表学报，2005，26（8）：735-737.

[15] McCartney E J.Optics of atmosphere：Scattering by molecoles and particles[M].New York：John Wiley and Sons，1976：23-30.