基于神经网络PID的液动调节阀控制研究

2015-04-16顾寄南

机械制造 2015年6期

□ 周培 □ 顾寄南

江苏大学制造业信息化研究中心江苏镇江 212013

液动调节阀在石油、化工和船舶等行业中的地位十分重要，它能够对温度、流量、压力等被控变量进行控制。而阀门控制器作为其重要附件之一，可以改善阀门特性，提高控制精度和速度，增加控制的灵活性。传统阀门定位器采用常规PID控制，控制算法简单，容易实现。但由于液压系统所处环境极其复杂，有许多不确定因素，难以建立精确的数学模型，因此传统PID已经难以满足控制要求。为了提高液压控制系统的稳定性，克服传统PID的缺点，本文引入BP神经网络，设计出具有自适应能力的智能PID控制系统。

1 液动调节阀控制原理

液动调节阀控制原理如图1所示，被控对象是液动调节阀。将输入控制信号r（4～20 mA电流信号）与通过传感器测到的角度反馈值ym进行比较，当偏差为e时，通过A/D信号转换，输出信号u来调节阀的转动，最终准确达到阀芯所需要的位置。

▲图1 阀门控制器工作原理

2 基于BP神经网络整定的PID控制

2.1 BP神经网络PID控制系统结构

基于BP网络的PID控制系统结构如图2所示，控制器由两部分构成：经典的PID控制器和BP神经网络学习算法。前者直接对被控对象进行闭环控制，后者是根据系统的运行状态，调整PID控制器的参数，从而达到性能指标的最优化，使输出层神经元的输出状态对应于PID控制器的三个参数kp、ki、kd，通过神经网络的自学习和加权系数调整，使神经网络输出对应于某种最优控制规律下的PID控制参数。

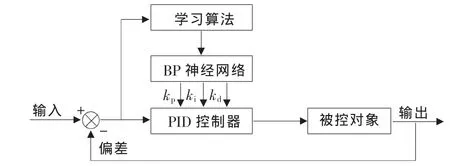
▲图2 基于BP神经网络PID控制器结构

经典增量式数字PID的控制算法为：

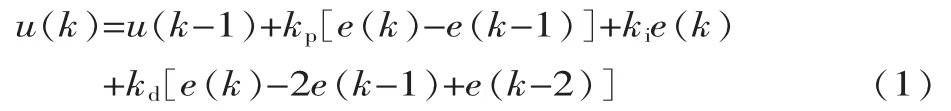
式中：kp、ki、kd分别表示比例、积分、微分系数。

2.2 BP神经网络结构

本文采用三层BP神经网络，其结构如图3所示。

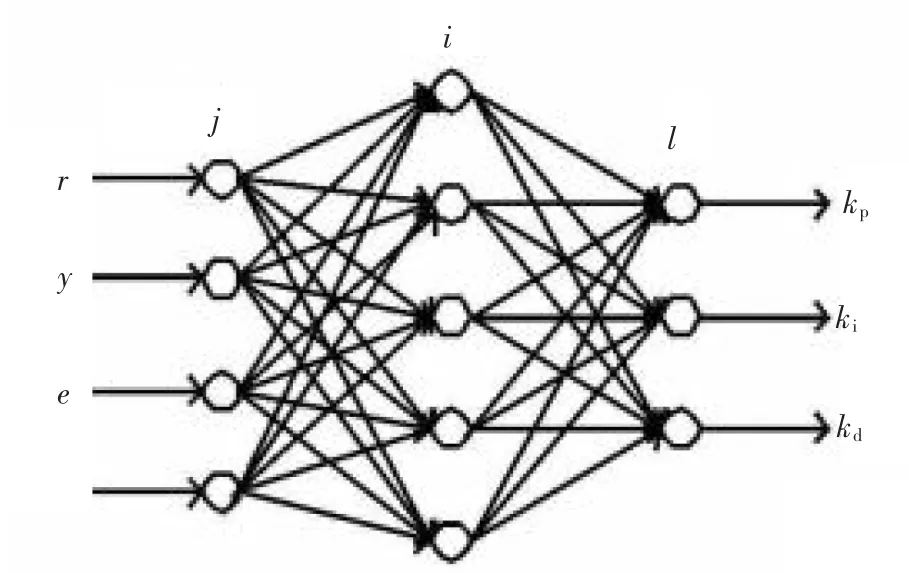
▲图3 BP网络结构

网络输入层的输入为：

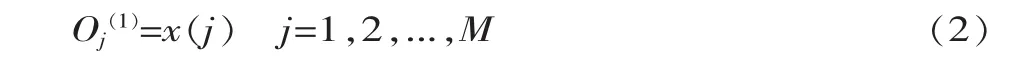
式中：x（j）为给定网络输入；M为输入层节点数，根据被控对象的复杂程度，选取M值为4。

网络隐含层的输入为：

隐含层的输出为：

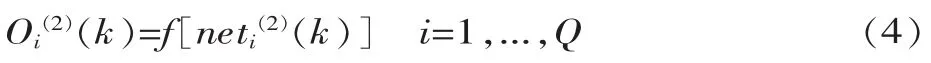
式中：wij（2）为隐含层的加权系数，上角标（1）、（2）分别代表输入层、隐含层。

隐含层神经元的活化函数取正负对称的sigmoid函数：

网络输出层的输入为：

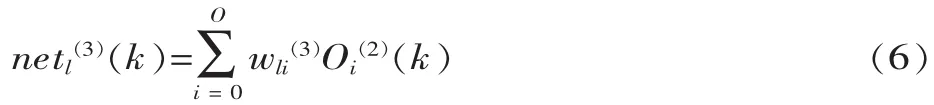
输出层的输出为：

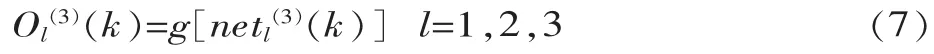
式中：wli（3）为输出层加权系数，上角标（3）代表输出层。

输出层的3个输出分别对应PID控制器的3个参数，即：

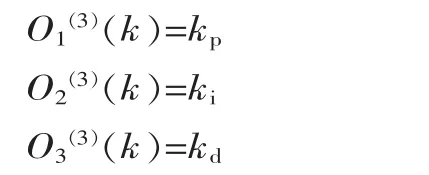
因为PID控制器的3个参数均不能取负数，所以输出层神经元活化函数为非负的sigmoid函数，即：

取性能指标函数为：

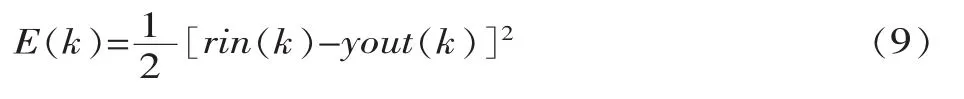
3 系统仿真

液动调节阀采用闭环液压伺服控制，根据已知参数及液压系统的特点，推导出闭环传递函数为：

▲图4 常规PID阶跃响应曲线

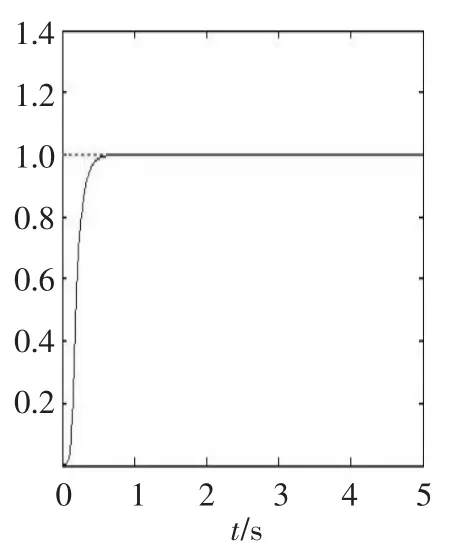
▲图5 神经网络PID阶跃响应曲线

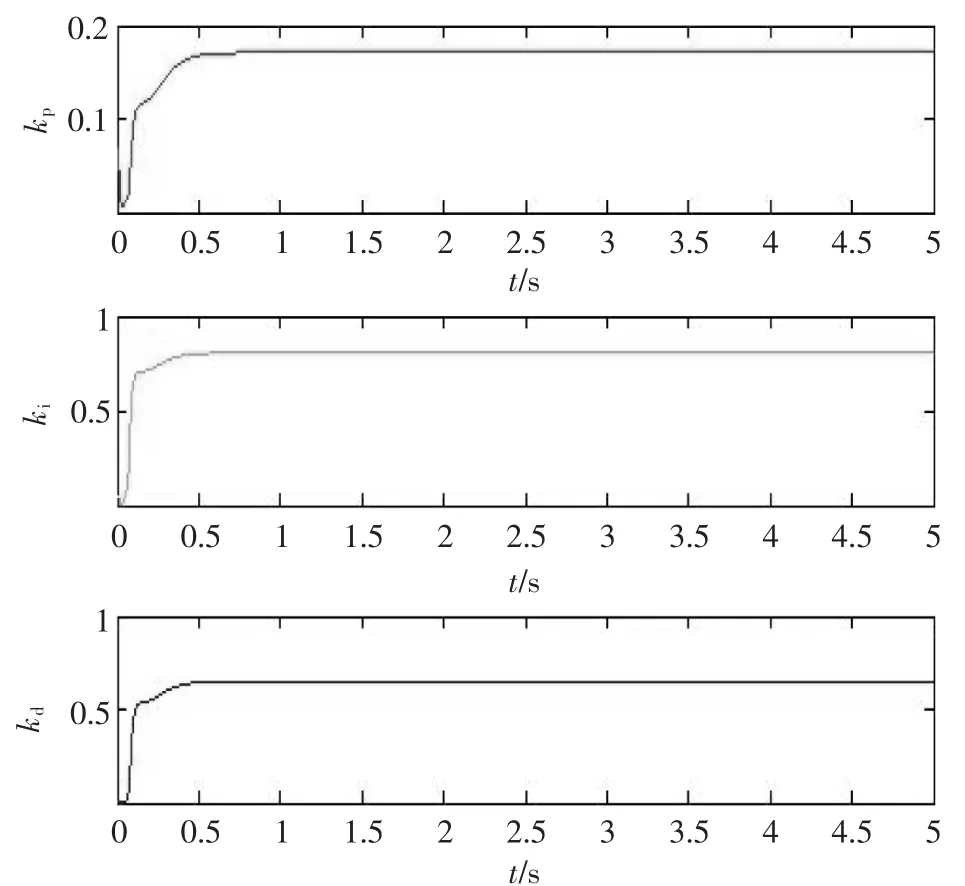
▲图6 参数自适应曲线

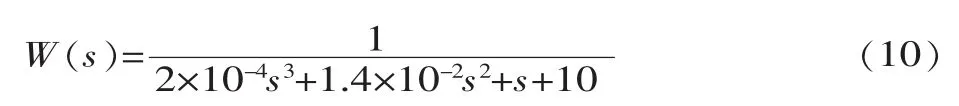
通过MATLAB/Simulink对常规PID仿真，结果如图4所示。针对神经网络PID，本文选用3层网络，网络结构为4-5-3，学习速率为0.28，惯性系数为0.04，加权系数区间为［-0.5～0.5］之间的随机数，编写神经网络程序后，输入阶跃响应信号，其阶跃响应曲线如图5所示，参数自适应曲线如图6所示。

由图4和图5对比可知，常规PID出现了较大的波动，而且趋向稳定的时间较长。BP神经网络PID几乎没有超调量，而且很快达到稳定状态。