无人机S弯进气道流动分离的数值模拟
2015-04-16田晓平潘鹏飞
□ 田晓平 □ 潘鹏飞 □ 田 琳
中国飞行试验研究院 发动机所 西安 710089
现代战斗机进气道的设计,为了达到总体布局和隐身性能等多方面的要求,大都采用S弯进气道,S弯进气道已经成为进气道设计中的典型形状。但自从上世纪80年代末Tornado飞机试飞中,在不同飞行条件下,左、右发动机先后发生了喘振,之后进行的大量研究表明,喘振是由进气道旋流引起的[1-5]。随后在“战斧”巡航导弹[6]、A300 的 APU[7]上再次验证了旋流对发动机稳定性的影响,而其共同的特点是采用了S弯进气道。S弯进气道由于长度短、拐弯急,具有总压恢复系数低、流场畸变大的特点。当吸入前机身的来流附面层后,附面层低能流体在管道曲率变化较大的区域,容易出现流动分离,进一步加剧流场畸变。已有的研究表明:S弯进气道是导致旋流产生的一个很重要的因素[8,9]。旋流是进气道/发动机相容中危害最大的干扰参数[10-12],反向旋流(与发动机旋转方向相反)的出现会直接导致发动机失速喘振甚至熄火停车,同向旋流的出现会导致发动机推力的下降,长期处于对涡旋流中的发动机极易出现高循环疲劳失效(HCF)[13]。
本文针对某型无人机S弯进气道进行了三维流场数值模拟计算研究和进气道三维流动特性研究。
1 进气道数学模型
流体力学的基本物性关系(密度、比热、导热系数、黏性系数等)与流体运动所遵守的基本物理定律(质量守恒定律、动量守恒定律、能量守恒定律)的数学描述,构成了流体力学运动的基本方程组。
本文计算的进气道是某型无人机S弯进气道,如图1所示。三维计算域如图2所示,进气道前端由长为40 m、直径为15 m的圆柱体围起来,以对进气道内外流场统一求解[14-15]。飞机在空气中飞行,可以看成为飞机静止,空气相对飞机运动,计算的流体即为空气。
整个计算区域使用结构性网格,靠近进气道壁面的边界层网格第一层厚为1 mm,之后逐层增厚,比例系数为1.2,共6层。进气道以外的网格逐渐由细网格过渡到外场的粗网格,以减小整个计算域的网格数量。整个计算网格数为80万,如图3所示,图4为局部网格示意图。
本文用FLUENT软件进行计算,采用标准k-ε湍流模型加壁面函数的方法,圆柱体侧面和离进气道进口较远的底面为远场边界条件,进气道入口所在的圆柱体底面使用压力出口,进气道出口也是压力出口。

▲图1 进气道CFD几何模型

▲图2 计算域和边界条件

▲图3 整个计算区域网格

▲图4 局部网格示意图
1.1 控制方程
(1)连续方程。

(2)动量方程。

(3)能量方程。
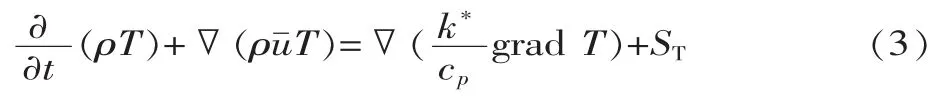
式中:ρ为密度;t为时间;▽为散度;u为速度矢量;u为速度值;p 为压力;τxx、τyx、τzx分别是黏性力 τ 的分量;Fx为微元体上的体力;cp为比热容;T为温度;k*为传热系数;ST为热能;grad为梯度。
(4)湍流模型。目前,湍流模型以标准k-ε湍流模型应用最为广泛,标准k-ε模型适于计算高雷诺数湍流,此模型已在工程计算中得到广泛应用,其准确度和可靠性也得到了较多实验数据的验证。本文所计算的均为高雷诺数湍流工况,所以采用此种湍流模型,其输运方程为:

式中:k为湍动能;ε为湍动能耗散率;Gk为湍动能生成项;YM为扩张耗散项;μ为流体黏性系数;μt为计算涡黏性系数;C1ε、C2ε、δk、δε、K 为常数,分别为:C1ε=1.44、C2ε=1.92、δk=1.0、δε=1.3、K=0.040 4。
(5)壁面处理。采用k-ε二方程模型计算时,对于壁面附近的区域,为了避免在壁面附近采用很细的网格而导致过大的计算量,采用壁面函数法处理,它能节省内存与计算时间,在工程紊流计算中应用较广。
标准壁面函数对高Re数,由壁面限制的流动给出了合理准确的解。本文所计算的工况雷诺数较高,同时为了避免在壁面附近采用很细的网格而导致过大的计算量,节省内存与计算时间,所以在计算中选取的壁面函数是标准壁面函数,它是基于Launder和Spalding的模型,已被广泛应用于工程计算。
1.2 畸变的表示方法
流场畸变指数是衡量进气道性能好坏的参数之一。进气畸变对发动机工作的影响主要是改变发动机的稳定边界,一般是使稳定边界下移,减小发动机的稳定裕度,影响发动机的气动稳定性。本文采用以下两种畸变指数。
1.2.1 总压畸变表示法
主要采用俄罗斯国内统一的总压畸变表示方法,即综合畸变指数:

式中:σ0为低压区内的平均总压恢复系数,是低压区内平均总压与进气道前未扰动气流总压之比;σav为发动机进口气动界面上的面平均总压恢复系数;P(t)为界面测量点上随时间变化的总压值;Pav为时间TU内该测点的总压平均值;TU为脉动气流的取样时间。
本文计算的工况均为稳态工况,同时周向总压畸变指数占畸变指数的主要部分,所以以下所给出的总压畸变指数均为稳态周向总压畸变指数。
1.2.2 旋流畸变指数
旋流畸变指数用旋流系数表示,其定义为:在发动机进口界面上按60°扇形范围计算得出的气流平均横向速度的最大周向分速度除以进气道喉道截面的气流速度,横向气流的周向分速,顺时针方向(向下流看)为正值,反之为负值,表示式为:式中:为按60°扇形区进行计算得出的气流横向速度的最大周向分速平均值;Vth为进气道喉部的气流速度。

1.3 边界条件
本文涉及到的边界条件有壁、压力出口和压力远场3种。
(1)壁边界条件。前机身表面、进气道表面都使用壁边界条件,采用无滑移、静止的、绝热的、光滑的壁。
(2)压力出口边界条件。压力出口边界条件需要在出口边界处指定静压,进气道出口截面气流速度均为亚音速状态,计算中根据实验数据给出其值为61.9 kPa。
(3)压力远场边界条件。本文所计算工况的速度为0.7Ma,飞机空气绕流流场的外边界设成压力远场边界,在压力远场边界上给定压强、温度、流动速度(马赫数)和流动方向。根据气动表查得高度为5 500 m高空时空气的参数:压强p=50 539 Pa、温度T=252.4 K。
2 计算结果分析与讨论
为了了解S弯进气道中气流的流动情况,从而对进气道中出现的流动分离现象施加流动控制,并获得最优控制方案的几何参数,必须研究进气道内部流场三维流动特征及造成其内部流动发生流动分离的流体力学机制,因此要对进气道内部三维流场作分析。
2.1 总性能
数值计算结果见表1。

表1 性能数值计算结果

▲图5 不同轴向截面总压分布

▲图6 不同轴向截面马赫数分布
从计算结果可以看出,进气道后总压恢复系数较低,旋流畸变指数很高,达到0.091。这样的出口流场会严重影响发动机的稳定工作。为了更清楚地认识气流在进气道中的流动情况,因此需要研究S弯进气道内部的三维流动情况。
2.2 三维流动特性
为了分析、研究S弯进气道内部流动特性,图5、图6给出了进气道不同轴向位置横截面的总压和马赫数分布云图。
由图5、图6可见,进气道下壁面的低总压区的面积,亦即边界层厚度,沿着流体流动的方向是不断增大的,增大幅度缓慢,并且其边界层内部的流动没有出现流动分离。然而,进气道上壁面低总压区的面积,亦即边界层厚度,沿着流体流动的方向,先是不断增大,增大幅度很快,当其增大到一定程度,并在由横向压力梯度诱导出的强二次流动和流向强逆压梯度的共同作用下,在进气道上壁面出现大面积的流动分离,充满整个进气道的上壁面(如图5所示)。随后,由于大面积分离流动的出现,下壁面低总压区的周向尺度迅速增大,在这个过程中,分离区内会生成两个反方向旋转的强三维的流向涡(如图7所示)。流向涡在往进气道出口方向进行传播的过程中,在旋涡旋转的作用下,会不断把通道主流中的高能量(高总压)的流体卷吸进来,使之与流向涡的低能量(低总压)流体发生激烈掺混,对流向涡内部的低能量流体不断进行充能,从而使流向涡在往下游进行传播的过程中,其内部低压流体的总压会不断增大,并且流向涡的涡量更加集中。这种流动结构会一直持续到进气道出口,并最终在进气道出口截面形成一个周向角度约为60°的低总压畸变区,造成进气道出口的流场很不均匀。与此同时,在流向涡底部流体的抬升作用下,沿着轴向增大的方向,流向涡核的径向坐标是不断增大的,亦即流向涡是不断向通道中心进行扩散传播的。

▲图7 S弯进气道出口二次流分布图

▲图8 S弯进气道对称截面流线图
另外,为了进一步提高对促使进气道上壁面边界层发生流动分离的流动机理及其流动分离所诱导出的流向涡结构的认识,图8给出了S弯进气道对称截面上的流线图,展示了流向涡的形成、发展及其传播过程。
3 结论
在S弯进气道内部流动中,在由横向压力梯度作用而诱导出的横向二次流和流向逆压梯度的共同作用下,S弯进气道上壁面边界层内部的低速流体发生大面积的流动分离,并在横向二次流的驱动作用下,分离区内部的流体被卷起形成一对旋向相反的流向涡结构,并在进气道主流的输运作用和旋涡本身的旋转作用下,流向涡逐渐增大,一直持续到进气道的出口,并在进气道出口截面形成一个角度约为60°的周向低总压区,亦即是周向总压畸变区。
由此可见,进气道上壁面边界层内部的流体发生大面积的流动分离而被卷起形成的两个旋向相反的流向涡是造成S弯进气道产生流动损失及其出口流场不均性的主要根源。因此,为了降低S弯进气道的流动损失和提高进S弯进气道出口流场的品质,就必须对通道中出现的流向涡进行控制。基于这一目的,必须开展流动控制技术对S弯进气道的三维分离流动进行流动控制研究工作。
[1] Aulehla F.Intake Swirl-a Major Disturbance Parameter in Engine/intake Compatibility [C].Proceedings of the 13th Congress of ICAS/AIAA,Seattle,1982.
[2] 芮长胜,谷君,邱明星,等.2种进气畸变流道结构对航空发动机[J].航空发动机,2013,39(5):42-46.
[3] 胡骏,赵运生,丁宁,等.进气畸变对大涵道比涡扇发动机稳定性的影响[J].航空发动机,2013,39(6):7-12.
[4] 谢静,范文正,谢镇波.某型军用发动机使用可靠性评估[J].航空发动机,2012,38(6):43-47.
[5] 郑波,朱新宇.航空发动机故障诊断技术研究[J].航空发动机,2010,36(2):22-25,30.
[6] Ludwig G R.Case Studies on Effect of Inlet Swirl on Engine Operability [R].Report to the S-16 Committee of the SAE,1993.
[7] Lotter K W,Jorg J.The Effect of Intake Flow Disturbances on APU Compressor Blade High Cycle Fatigue in the Airbus A300 [C].Proceedings of the 13th Congress of ICAS/AIAA,Seattle,1982.
[8] Beale D K,Cramer K B,King P S.Development of Improved Methods for Simulating Aircraft Inlet Distortion in Turbine Engine Ground Test[R].AIAA Paper,2002-3045,2002.
[9] 杨国才.在流场匹配方面进气道反旋流措施的工程应用研究[J].推进技术,1994(2):17-24.
[10]杨国才.在进气道与发动机相容性方面反旋流措施的工程应用研究[J].推进技术,1995(4):28-33.
[11] 杨国才.S弯进气道和发动机相容性 [J].推进技术,1996(6):26-29.
[12] Stocks C P,Bissinger N C.Design and Development of Tornado Engine Air Intake[R].AGARD-CP-301,1981.
[13]郭东明,刘振侠,吴丁毅,等.三维进气道湍流流场数值模拟[J].航空计算技术,2006,36(1):90-93.
[14] 刘振侠,郭东明,张丽芬,等.S 形进气道流场数值模拟[J].航空动力学报,2006,21(6):1064-1068.
[15]郭东明.超音速S形进气道流场数值模拟[D].西安:西北工业大学,2006.
(编辑 日 月)
