新型面积差法光伏MPPT

吴增强，邹海荣，魏浩

（上海电机学院电气学院，上海 200240）

太阳能作为一种可再生、无污染、蕴含量大的清洁能源，具有很好的应用前景。由于光伏电池的结构特点，它的输出P-U特性曲线具有明显的非线性，在不同的条件下有不同的最大功率点[1]；当外界光照或者温度变化时，最大功率点也相应地变化，为了保证光伏电池输出功率始终处于最大功率点，必须对光伏电池的输出进行最大功率点跟踪MPPT（maximum power point tracking），以此来提高光伏发电系统的效率。

目前国内外常用最大功率跟踪方法有开环和闭环两种方法。开环方法主要有定电压法CV（constant voltage）[2]和短路电流法SEC（short circuit current）[3-4]。这些方法跟踪速度快，但是对光伏电池的输出特性具有较强的依赖性，并且只能近似地跟踪，效率不高。常用的闭环方法有扰动观察P&O（perturbation and observation）和电导增量INC（incremental conductance）法。这些算法利用在正常不同光照的条件下，光伏电池的P-U特性曲线是一簇以不同最大功率点为极值点的单峰值函数，在最大功率点处时有d P/d U=0，即通过自寻优来满足d P/d U=0[5-6]。但是当外界环境发生巨变，或者光伏电池被部分遮挡时，上述方法可能产生振荡或者误判[7]。随着智能控制的发展，模糊逻辑法[8-9]以及神经网络预测法[10-11]等不断地被应用于光伏最大功率跟踪。智能方法适应性较强，但是结构复杂且对硬件电路要求较高，例如神经网络预测法还需要长时间的训练.

本文在分析光伏电池P-U输出特性曲线的基础上，提出一种新型基于面积差自适应调节扰动步长最大功率跟踪方法，该方法通过连续采样光伏电池P-U特性曲线上的点所对应的面积差，自适应地调节扰动步长。Matlab/Simulink的仿真结果验证了该方法的正确性，与扰动观察法的结果比较验证了所提出方法的优越性。

1 光伏电池模型及输出特性

1.1 光伏电池模型

光伏电池光电转换原理基于半导体PN结的光伏效应：当半导体处于光照时，半导体内的电荷分布状态随之发生改变而产生相应电动势与电流的一种能量转换效应。光伏电池等效电路[9]如图1所示。

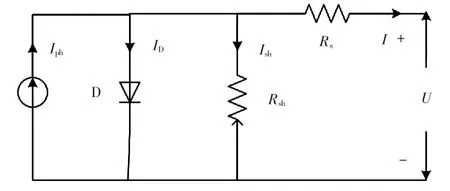
图1 光伏电池等效电路Fig.1 Equivalent circuit of photovoltaic cells

图1中，I为光伏电池的输出电流；Ish为流过电阻Rsh的电流；ID为流过二极管D的电流；Iph为光生电流；U为光伏电池的输出电压；Rs、Rsh为电池内部的等效电阻。以图中的电流方向为参考方向，则

式中：A为光伏电池P-N结系数；I0为光伏电池反向饱和电流；K为玻耳兹曼常数；θ为光伏电池温度。

根据式（1）和式（2），经过化简，利用Matlab/Simulink对某型号光伏模块进行建模并仿真分析。在不同光照S、温度条件下，光伏模块的I-U、P-U仿真特性曲线如图2所示。

从图2中可见，图（a）中，温度对光伏电池的短路电流影响不大，随温度的增加，光伏电池短路电流略微增加；开路电压随温度的增加而减小。图（b）中，光照对光伏电池的短路电流影响较大，短路电流随外界光照的增加而变大，且变化范围较大；开路电压随光照的增加而略微增加。图（c）中，在光照相同的情况下，光伏电池输出功率随温度的增加而减小，在一定环境下只有一个最大功率点且在最大功率点的左侧输出功率与输出电压近似呈线性关系。图（d）中，在温度相同的情况下，光伏电池的输出功率随外界的光照强度增加而增加，不同光照下最功率点的电压变化不大。

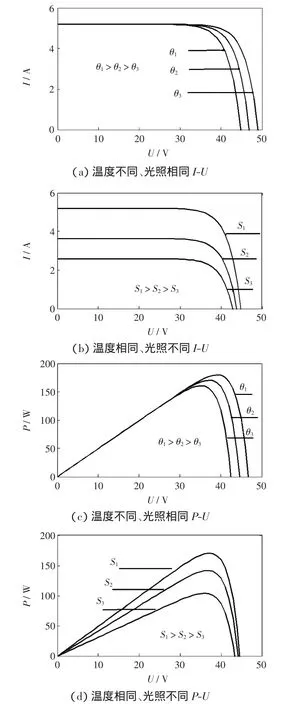
图2 光伏电池在不同条件下的特性曲线Fig.2 Characteristics of photovoltaic cells under different conditions

2 光伏发电系统最大功率跟踪研究

2.1 光伏最大功率点分析

由于外界温度、光照不断变化，光伏电池的最大功率点也不断变化；当光伏电池的输出阻抗与负载阻抗相等时，光伏电池输出功率最大，完成了最大功率点的跟踪。为了实现光伏发电系统工作在最大功率点，需要实时调节光伏发电系统的负载阻抗。一般而言，光伏发电系统的负载阻抗不易改变，因此需要通过变换器来改变光伏电池的输出阻抗，实现光伏电池输出阻抗与负载阻抗的匹配。Boost电路以其转换效率较高而作为常用的MPPT变换器，基本电路[12-13]如图3所示

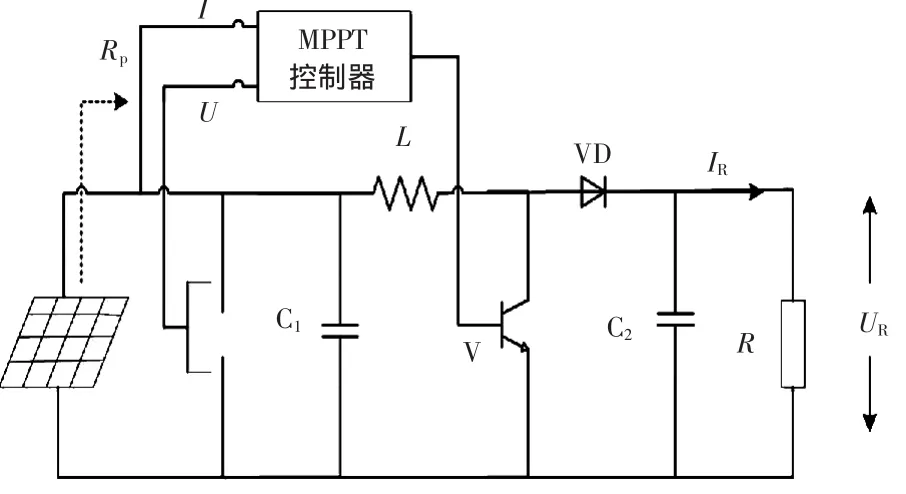
图3 基于Boost电路的MPPT原理Fig.3 Principle of MPPT based on Boost conversion

设光伏电池的输出电压为U，输出电流为I；负载电压为UR，负载电流为IR，光伏电池的输出阻阻为Rp，光伏发电系统负载电阻为R，电路的占空比为D。则当电子元器件工作在理想状态下时有

由式（3）、式（4）得

由式（5）可知，当外界环境不断变化时光伏电池的输出阻抗不断变化，通过改变占空比D可实现光伏电池的输出阻抗与负载阻抗匹配，即实现光伏电池的最大功率跟踪。

2.2 面积差调节扰动步长M PPT算法实现

扰动法是光伏电池最大功率跟踪常用的方法，基本原理是通过改变扰动步长来实现最大功率跟踪。根据光伏电池的输出P-U特性提出基于面积差自适应调节扰动步长，该方法通过连续采样点构成的2个四边形的面积差来实现扰动步长变化量的自寻优。在不同环境下光伏电池的3条P-U特性曲线如图4所示。S（K-1）、S（K-2）为连续采样点所构成的四边形面积，面积差ΔS为

由式（6）可知，当连续采样点离最大功率点较远时，面积差较大；当连续采样点A、B、C离最大功率点较近时，面积差ΔS较小；当连续采样点在最大功率点附近时，面积差ΔS几乎为0；当连续采样点同时在最大功率点上时，面积差ΔS为0。根据上述规律，提出以连续采样点所构成四边形的面积差ΔS与扰动灵敏度a的乘积作为最大功率点跟踪的步长变化量。

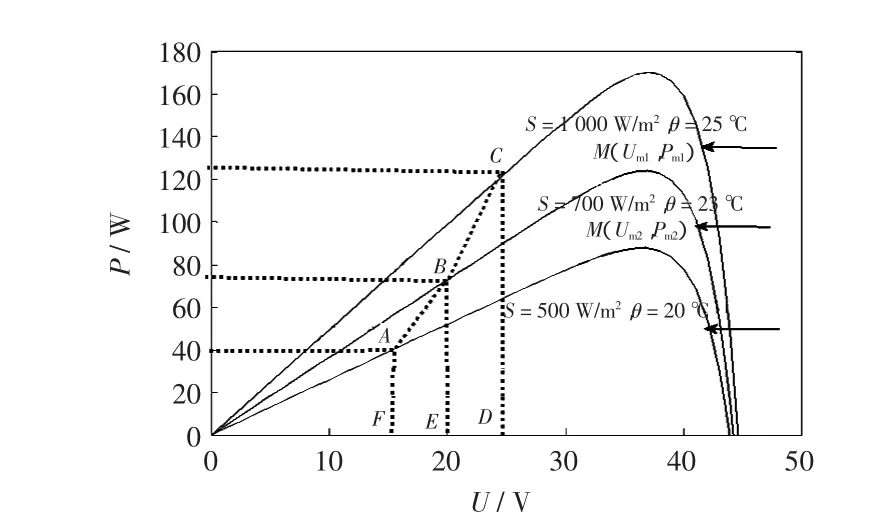
图4 不同条件下光伏电池P-U特性曲线Fig.4 P-U characteristics curves of photovoltaic cells under different conditions

图4中设光伏电池P-U输出特性曲线上相邻3个采样点的坐标分别为：A（U（K-2），P（K-2）），B（U（K-1），P（K-1）），C（U（K），P（K）），其中K为大于2的正整数，U为光伏电池输出电压，P为光伏电池输出功率。最大功率点M的坐标M（Um，Pm）。点A在P-U输出特性曲线的U坐标轴上的投影为点F，点B在U轴的投影为点E，点C在U轴投影为点D。线段AB、BE、EF、FA组成四边形ABEF，其面积为S（K-2）；线段BC、CD、DE、EB组成四边形BCDE，其面积为S（K-1）；第3个采样点C采样后，系统最大功率跟踪扰动步长变化量ΔD为

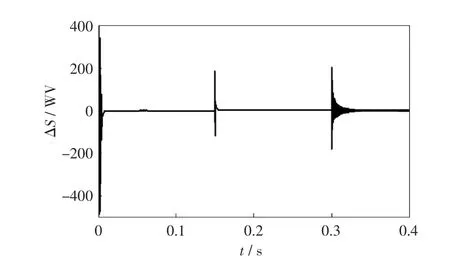
式中：ΔP=P（K）-P（K-1）；a为扰动灵敏度，0

（1）当ΔP＞0时，由式（7）得系统的下一个功率跟踪扰动步长变化量ΔD为

由式（8）知，系统扰动步长变化量ΔD随面积差ΔS大小改变而改变。当ΔS较大时，ΔD较大，此时跟踪速度较快；当采样点接近最大功率点ΔS较小，ΔD较小，此时跟踪时振荡较小，可以减小功率损失。

（2）当ΔP=0时，采样点A、B、C在最大功率点M（Um，Pm）上，系统扰动步长变化量ΔD=0，此时驱动电力电子开关的PWM信号占空比不变，系统输出电压不变，系统工作在最大功率点处。

（3）当ΔP＜0时，采样点C在最大功率点M（Um，Pm）的右边，采样点A、B在最大功率点左右位置不定。由式（7）得

由式（9）可知，系统扰动步长变化量ΔD随面积差ΔS大小改变而改变。当ΔS较大时，ΔD较大，此时从反方向较快的速度靠近最大功率点；当采样点接近最大功率点时，ΔS较小，ΔD较小，此时跟踪时振荡较小，可以减小功率损失。D（K）为系统下一个扰动步长，D（K－1）为系统当前扰动步长，整个算法的流程如图5所示。

图5 整个算法控制流程Fig.5 Flow chart of the whole algorithm control

3 控制算法验证分析

为了验证上述方法的有效性，对某型号光伏模块进行建模并仿真分析。其模型参数为：短路电流5.2 A；最大功率点电流4.9 A；开路电压44.2 V；最大功率点电压35 V；在θ=25℃、光照S=1 000 W/m2条件下最大功率约为171.5W。根据图3，在Matlab/Simulink搭建了光伏电池MPPT整个系统仿真模型。其中系统采样时间T=0.000 1 s，电容C1=10μF，电感L=10mH，电容C1=470μF，负载电阻R=18Ω，扰动灵敏的a=0.025，扰动观察法的初始扰动步长为0.05。

从0 s开始仿真，仿真时间设为0.4 s；在0～0.15 s，温度θ=25℃、S=1 000W/m2；在0.15～0.3 s，θ=20℃、光照S=800W/m2；在0.3 s时，环境温度不变，光照S变为600W/m2。图6为最大功率跟踪过程中自适应面积差法面积的变化。

图6 最大功率跟踪过程中面积差的变化Fig.6 Change of area difference during MPPT

由图6可见，在t=0～0.15 s，面积差ΔS自适应变化，总体逐渐减小；在t=0.015 s时，ΔS等于0并保持不变；在t=0.15 s、t=0.3 s时，外界温度、光照发生变化，ΔS快速变化并迅速变为0，从而证明了所提出方法的正确性。根据式（7），实现了扰动步长变化量随面积差的自适应变化。在外界环境发生较大的变化时，步长仍能迅速地调整。在跟踪到最大功率点处面积差为0时，扰动步长变化量为0，在最大功率处几乎没有振荡。

图7为自适应面积差法与扰动观察法在整个仿真过程中的比较，其中图7（a）为t=0～0.4 s2种方法下负载电流输出波形比较；图7（b）为t=0～0.06 s2种方法下负载输出电压波形比较；图7（c）为t=0～0.06s2种方法下负载输出功率波形比较。

图7 面积差法与扰动观察法仿真结果Fig.7 Simulation results of area difference method and P&O

从图7（a）中可见，在t=0～0.15 s时，面积差法完成最大功率跟踪，跟踪速度快。在t=0.15 s、t=0.3 s外界环境发生较大变化时，面积差法仍能快速完成最大功率跟踪，整个跟踪过程与图6中的面积差变化相符，从而证明了所提出方法的有效性。图7（b）中，在t=0.015 s左右时，2种方法均跟踪到最大功率点，且面积差法跟踪更快，随后扰动观察法的功率开始减小并按一定幅值振荡，面积差法的最大功率保持不变而且没有振荡。

4 结语

在分析光伏电池模型及其P-U输出特性曲线的基础上，结合升压Boost电路，提出了一种变步长光伏MPPT方法，该方法能够快速实现对光伏电池最大功率点的跟踪。当外界环境如光照发生很大变化时，光伏电池的P-U曲线会发生相应改变；此时面积差也会随之变化，依据提出的跟踪方法系统将以新的步长、较快地跟踪到新的最大功率点。当连续采样点在最大功率点附近时面积差几乎为0，扰动步长的变化量几乎为0，则扰动步长变化量接近0，减少了功率跟踪过程中振荡及功率损失。当连续采样点在最大功率点上时，面积差为0，扰动步长变化量为0，此时系统工作在最大功率状态且没有振荡现象及功率损失。利用Matlab/Simulink对所提出的算法进行仿真验证，并与常用的扰动观察法做对比。结果表明，所提算法跟踪速度更快、更准确，且系统不存在振荡。

[1]周林，武剑，栗秋华，等（Zhou Lin，Wu Jian，LiQiuhua，et al）.光伏阵列最大功率点跟踪控制方法综述（Survey of maximum power point tracking techniques for photovoltaic array）[J].高电压技术（High Voltage Engineering），2008，34（6）：1145-1154.

[2]熊远生，俞立，徐建明（Xiong Yuansheng，Yu Li，Xu Jianming）.固定电压法结合扰动观察法在光伏发电最大功率点跟踪控制中应用（MPPT control of photovoltaic generation system combining constant voltage method with perturb-observe method）[）[J].电力自动化设备（Electric Power Automation Equipment），2009，29（6）：85-88.

[3]张超，何湘宁（Zhang Chao，He Xiangning）.短路电流结合扰动观察法在光伏发电最大功率点跟踪控制中的应用（Shortcurrent combined with perturbation and observation maximum power point tracking method for photovoltaic powersystems）[J].中国电机工程学报（Proceedings of the CSEE），2006，26（20）：98-102.

[4]程启明，程尹曼，汪明媚，等（Cheng Qiming，Cheng Yinman，Wang Mingmei，et al）.光伏电池最大功率点跟踪方法的发展研究（Review on the MPPT method of PV battery）[J].华东电力（East China Electric Power），2009，37（8）：1300-1306.

[5]黄舒予，牟龙华，石林（Huang Shuyu，Mu Longhua，Shi Lin）.自适应变步长MPPT算法（Adaptive variable step size MPPT algorithm）[J].电力系统及其自动化学报（Proceedings of the CSU-EPSA），2011，23（5）：26-30.

[6]Soon Jin Jun，Key-Soon Low.Photovoltaic model identification using particle swarm optimization with inverse barrier constraint[J].IEEE Transon Power Electronics，2012，27（9）：3975-3983.

[7]朱志宇，原琳，陈迅（Zhu Zhiyu，Yuan Lin，Chen Xun）.遮蔽条件下的光伏阵列最大功率点跟踪算法（Maximum power point searching and tracking of partially shaded solar photovoltaic arrays）[J].电力系统及其自动化学报（Proceedings of the CSU-EPSA），2013，25（4）：63-67.

[8]朱铭炼，李臣松，陈新，等（Zhu Minglian，LiChensong，Chen Xin，et al）.一种应用于光伏系统MPPT的变步长扰动观察法（A variable step size P&OMPPT method for PV systems）[J].电力电子技术（Power Electronics），2010，44（1）：20-22.

[9]Ben Salah C，OualiM．Comparison of fuzzy logic and neural network in maximum power point tracker for PV systems[J]．Electric Power Systems Research，2011，81（1）：43-50．

[10]乔兴宏，吴必军，邓赞高，等（Qiao Xinghong，Wu Bijun，Deng Zangao，et al）.模糊/PID双模控制在光伏发电MPPT中应用（MPPT of photovoltaic generation system using fuzzy/PID control）[J].电力自动化设备（Electric Power Automation Equipment），2008，28（10）：92-95.

[11]Esram T，Chapman P L.Comparison of photovoltaic array maximum power point tracking techniques[J].IEEE Trans on Energy Conversion，2007，22（2）：439-449.

[12]程军照，李澍森，张腾飞（Cheng Junzhao，Li Shusen，Zhang Tengfei）.多路并网光伏发电系统的仿真与分析（Simulations and analysis on multi-branch grid-connected photovoltaic system）[J].电力系统及其自动化学报（Proceedings of the CSU-EPSA），2009，21（4）：58-62.

[13]赵争鸣，刘建政，孙晓瑛，等.太阳能光伏发电及其应用[M].北京：北京科学出版社，2010.