采用行波固有频率的混合线路故障测距新方法

黄忠棋

（福州大学电气工程与自动化学院，福州 350116）

目前，有关电缆-架空混合线路的故障测距的研究倍受关注。混合线路的测距方法多种多样，其中包括行波固有频率法[1-3]，该方法通过提取故障行波的固有频率主成分，再利用频率和距离的关系式来实现故障测距。由于电缆和架空线的波阻抗不一致，因此行波在故障点和线路连接点均会发生复杂的折反射现象，从而引起固有频率的混叠[4]。若不进行混叠消除，提取到的频率就不够精确甚至会有很大的误差。因此，消除频谱混叠是提高测距精度的首要问题。

解决频谱混叠问题的方法有盲源分离[5]、多重交织抽样[6]和经验模态分解EMD（empirical mode decomposition）[7-9]等，这些方法在一定程度上解决了频谱混叠问题。其中EMD被广泛地应用于电力系统中，消除频谱混叠的效果并不是很理想[7]。对此，本文提出将聚类经验模型分解EEMD（ensemble empirical mode decomposition）算法[10-11]运用到混合线路故障测距中，通过EEMD分解克服频谱混叠的问题，引入多重信号分类MUSIC（multiple signal classification）算法提取固有频率主成分，从而准确有效地实现精确的故障定位。

1 EEMD方法原理

1.1 EEMD方法介绍

根据文献[12]，利用EMD分解容易出现模态混叠现象，从而导致分解得到的固有模态函数IMF（intrinsic mode function）分量缺乏物理意义。对此，文献[13]提出了一种噪声辅助数据分析方法EEMD。该方法利用高斯白噪声频率均匀分布的特性，在分解的过程中不断加入白噪声，然后根据白噪声均值为零的特性，将所有的IMF多次求取平均值以消除外加的噪声，经过这一系列的增加消除白噪声，模态混叠的现象能得于避免。

EEMD的分解步骤如下：

步骤1将白噪声序列加在原始信号中；

步骤2将步骤1得到的信号进行EMD分解得到IMF；

步骤3每次加入不同的白噪声序列，反复重复步骤1、步骤2；

步骤4把分解得到的各个IMF的均值作为最终的结果。

1.2 EEMD的优势

为更加形象地说明EEMD在解决模态混叠现象中的效果，本文通过一个简单的仿真来比较EEMD和EMD方法。选取三相短路故障时C相信号加上10 dB的加性高斯白噪声，得到如图1所示的模态混叠的典型信号，该信号为在单位幅值的低频正弦中添加了高频扰动信号。

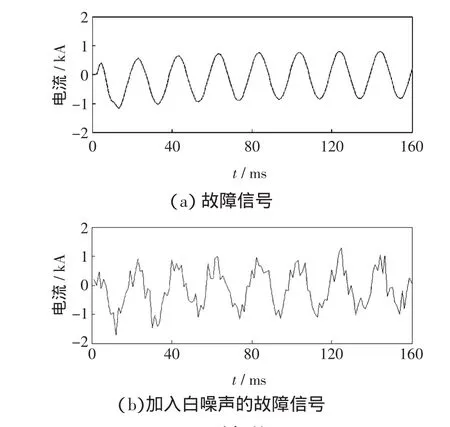
图1 对象信号Fig.1 Object signal

分别对图1所示的对象信号进行EMD分解和EEMD分解，得到一系列IMF分量。为方便比较，本文只提取两种算法的前4个IMF分量进行对比，分别如图2和图3所示。

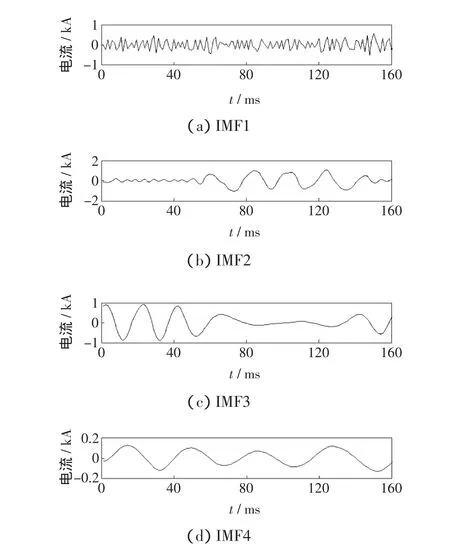
图2 EMD分解Fig.2 EMD decomposition

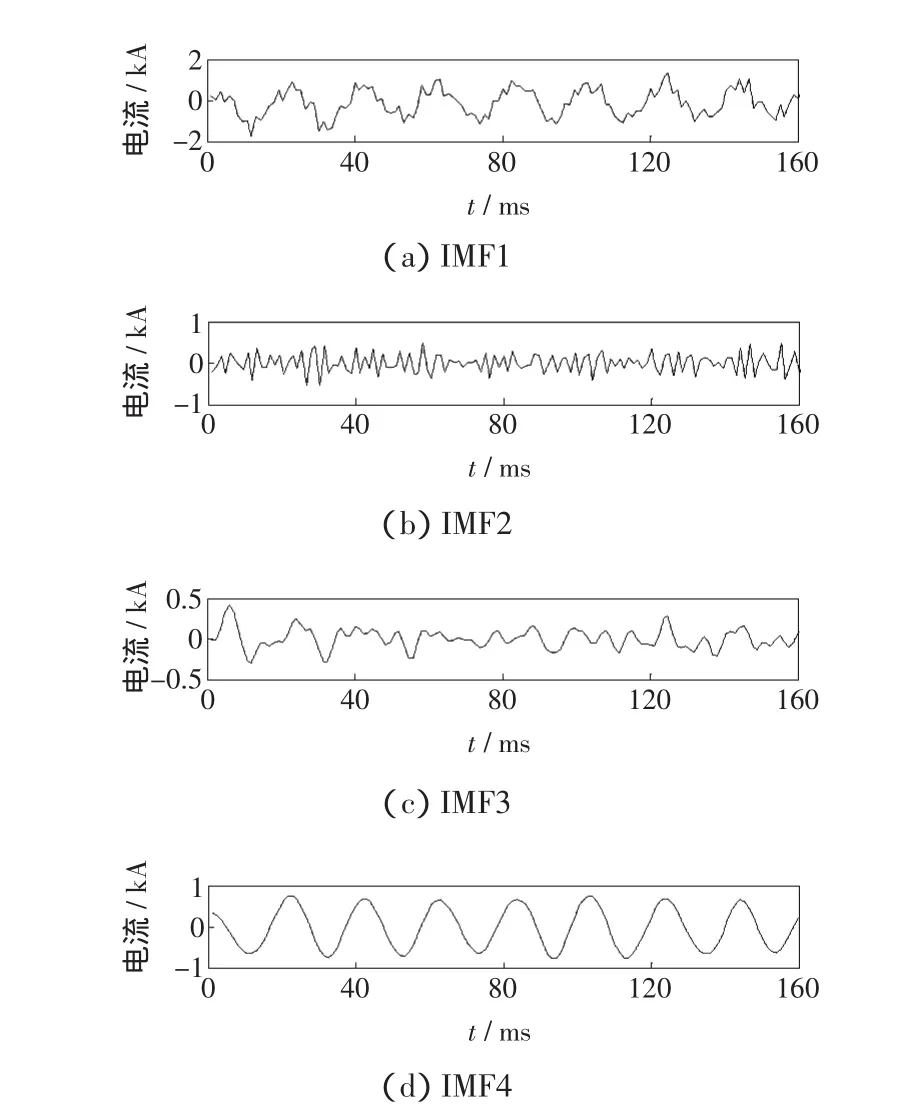
图3 EEMD分解Fig.3 EEMD decomposition

从图2可以看出，信号在经过EMD分解后，产生了严重的模态混叠现象；而图3中信号经过EEMD分解后，频率不相同的高频扰动信号和低频正弦实现了分离，从而避免了模态混叠现象。

因此，故障信号经EEMD分解后，故障特征信息便能很好地聚集在首个IMF分量中，再对该分量进行频谱分析即可提取故障行波的固有频率主成分。

2 混合线路故障测距方案

设混合线路由X段电缆和Y段架空线组成，每段线路的长度分别为L1，L2，…，LX+Y，各连接点与测量点（假设位于线路最左端）之间的长度为di，i=1，2，…，X+Y，即d1=L1，d2=L1+L2，…，dX+Y=L1+L2+…+LX+Y，如图4所示。

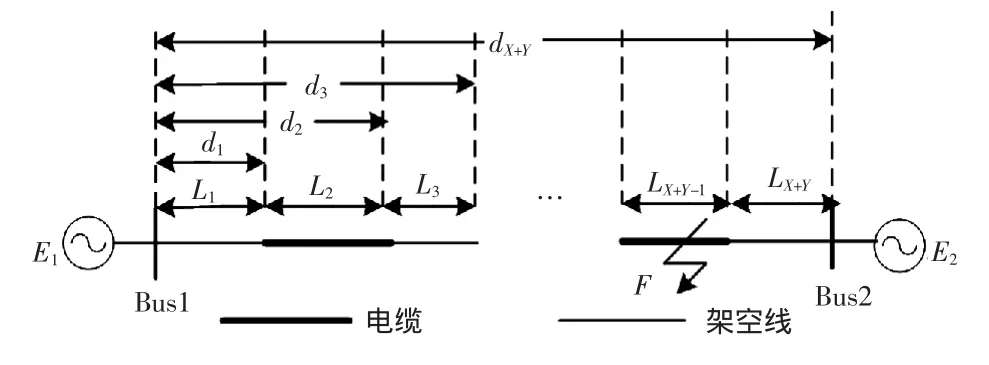
图4 多段混合线路示意Fig.4 Schematic diagram of multistage hybrid transmission line

测距方案的具体步骤如下：

步骤1对获取的故障电流行波信号进行EEMD分解，得到首个IMF分量；

步骤2利用MUSIC算法[14]提取该IMF分量的固有频率主成分fdf。该算法由于具备原信号外推能力，故与传统傅里叶变换技术相比，其频率分辨力可以摆脱采样点数以及时长的限制，特别适用于持续时间较短的故障信号。

步骤3分别计算该频率下的电缆和架空线的行波波速v1和v2；

步骤4分别计算在频率fdf下各区段的固有频率主成分频率，即

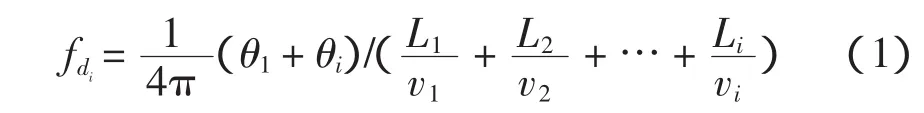
式中：θ1和θi分别为相应区段的始端和末端的反射角（若发生金属接地，取为π）；i为各区段编号，当i为奇数时，vi=v1；当i为偶数时，vi=v2；

步骤5进行故障区段判定，若fd(k+1)≤fdf≤fdk（k=1，2，…，X+Y－1），则区间k即为故障区段；

步骤6设故障区间k中故障点距离区间左端长为Lf，则有

化简后有

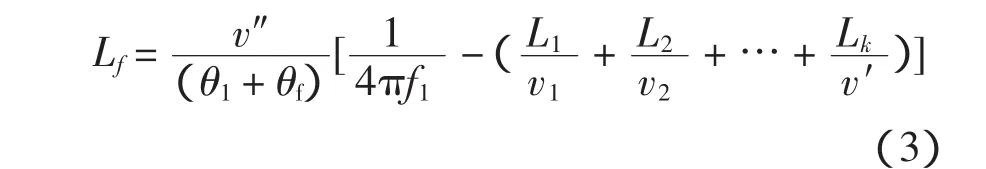
式中：θ1和θf分别为测量点和故障点的反射角；v1，v2，…，v′，v″分别为各个区段对应的行波传播速度，当k取奇数时，v′=v1，v″=v2，当k取偶数时，v′=v2，v″=v1。

步骤7因此，故障点到测量端的距离为

式中，dk-1为测量端到故障区段最左端的距离。

3 仿真算例

3.1 模型与参数

常见的电缆－架空线混合线路主要有4种类型，分别如图5所示。本文以经典的双电源A型混合线路作为分析和仿真对象。

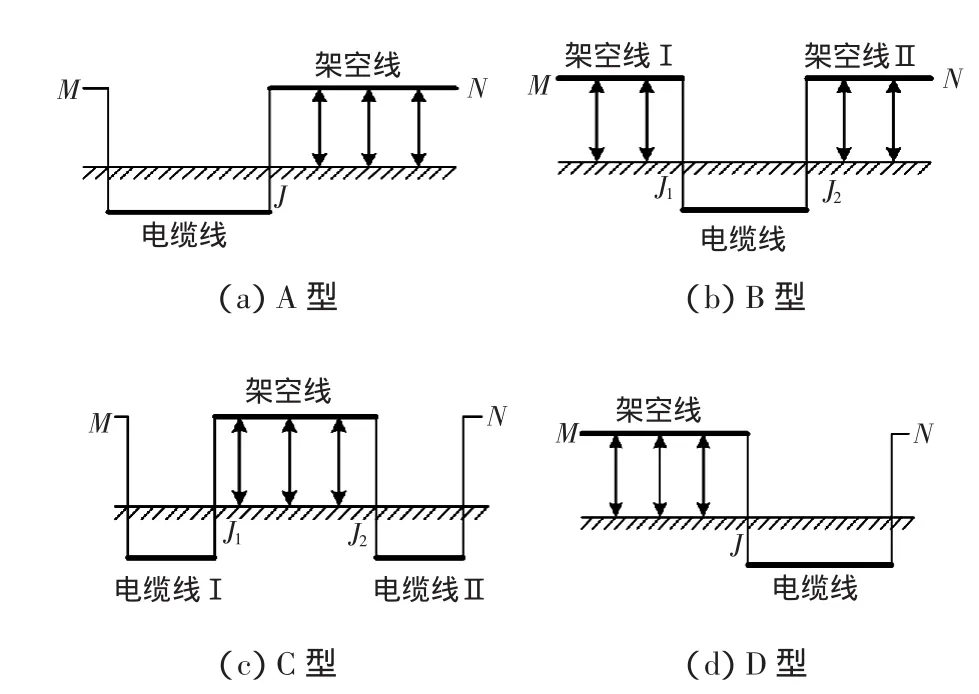
图5 电缆-架空线混合线路基本类型Fig.5 Basic types of cable and overhead line of hybrid transm ission line

由于线路发生故障后产生的暂态行波信号不仅频率很高而且频率所分布的范围也很广，因此考虑使用PSCAD/EMTDC中的频率相关的FD模型。架空线的塔杆选用3H5形式。电缆实际的结构比架空线复杂，截面参数有很多，根据文献[15]，利用PSCAD来搭建的电缆截面层数一般情况下只有4～6层，所以无需严格按照实际的截面来搭建电缆模型。电缆和架空线的参数取模块默认的参数。其中Bus1端电压源电压为500∠50°kV，Bus2端电压源电压为500∠30°kV，土壤电阻率为100 Ω·m。

利用图6所示的线路模型进行仿真。假设两端电源均为理想电源，即等效阻抗Z1=Z2=0，接地电阻为1Ω，线路在130 km处（架空段）发生ABC三相短路接地故障，故障发生时刻为0.034 s，在系统左端（测量端）以1MHz[16]的采样频率对暂态电流信号进行采样。

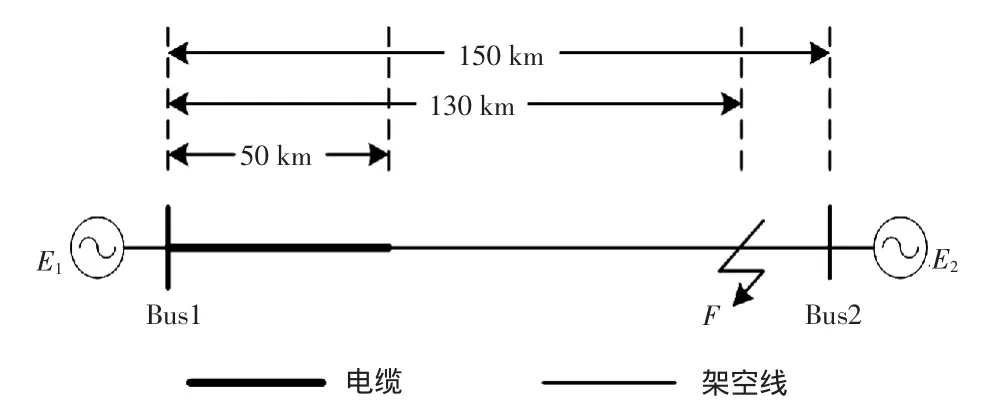
图6 A型混合线路示意Fig.6 Sketch map of type A hybrid transmission line

3.2 固有频率主成分的提取

为验证EEMD相比EMD更适用于混合线路故障测距，对采集得到的暂态电流信号进行克拉克变换，得到α模、β模和0模，根据故障信号的模量选取原则[17]，分别对故障行波的β模进行EMD和EEMD分解。分解后得到多个频率依次下降的IMF分量，由于反映故障特征的成分主要集中在首个IMF分量上，因此，只需对IMF1分量进行后续的测距相关步骤，两种算法分解得到的IMF1分量分别如图7和图8所示，利用MUSIC算法[14]得到的频谱分别如图9和图10所示。

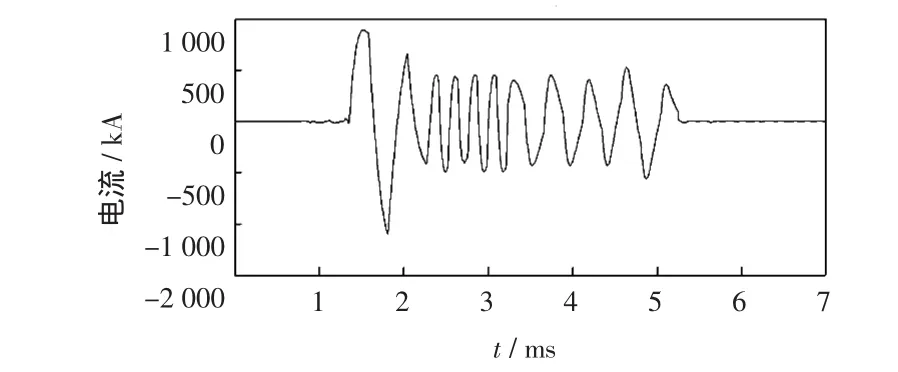
图7 IMF1分量EMD分解Fig.7 EMD decom position of IMF1

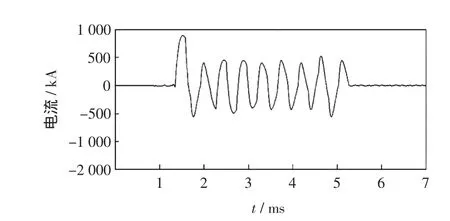
图8 IMF1分量EEMD分解Fig.8 EEMD decomposition of IMF1

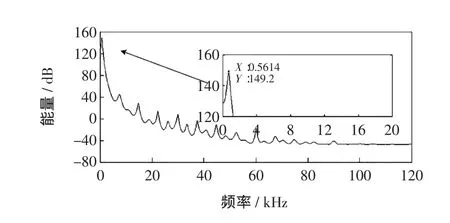
图9 EMD分解固有频率频谱Fig.9 Inherent frequency spectrum of EMD decomposition

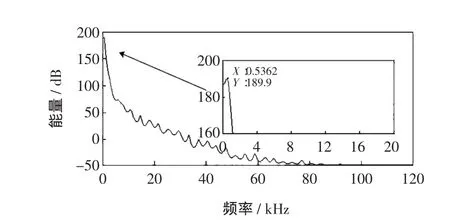
图10 EEMD分解固有频率频谱Fig.10 Inherent frequency spectrum of EEMD decomposition

从图7可以看出，经过EMD分解依然存在严重的后得到的频谱混叠问题，即IMF1分量中含有不同频率的信号；而图8所示的经过EEMD分解后得到IMF1分量频率大体一致，即无明显的频谱混叠现象，这表明了EEMD分解可以有效地改善EMD分解产生的频谱混叠问题。

由图9可见，首个峰值点位于fdf=561.4 Hz处，即固有频率主成分为561.4Hz，而从图10可得到EEMD算法的固有频率主成分为536.2Hz。由此可以看出，对于同样的故障信号，利用EMD算法和EEMD算法提取得到的固有频率主成分完全不同，在本算例中，两者相差了25.2Hz。

3.3 故障距离的计算

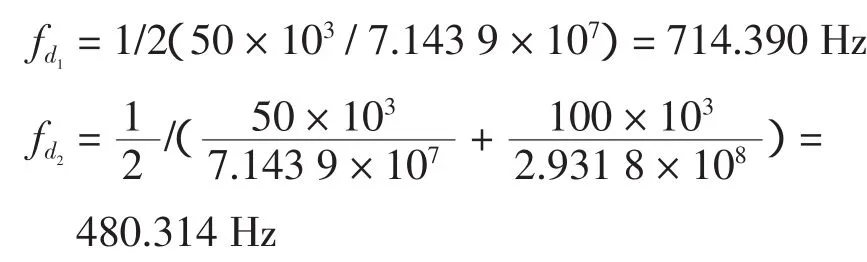
故障距离为df′=50+80.251=130.251 km。误差率为（130.251-130）/150=0.167%。

对于由EMD算法提取得到的固有频率主成分，依照上述计算步骤，可得到fdf=561.4Hz时所求的故障距离为df′=128.762 km，误差率为（130-128.762）/150=0.825%。

从本算例可以清楚地看到，采用EEMD算法的测距精度比采用EMD算法的测距精度提高了0.658%。

3.4 EMD和EEMD的结果对比

理论上由于EEMD算法解决了频谱混叠问题，因此其测距精度要比EMD算法的精度高，为了更好地证明这一点，本节分析不同状况对2种算法测量结果的影响。

（1）设过渡电阻为1Ω，故障处发生三相短路，则不同故障距离下2种算法的测量结果如表1所示。

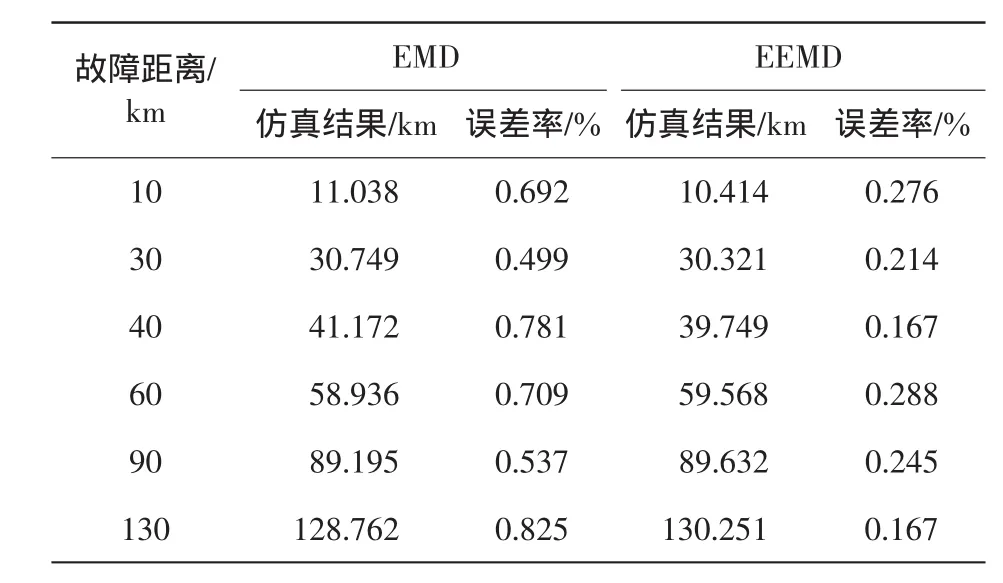
表1 不同故障距离下EMD和EEMD的测量结果Tab.1 Results by using EMD and EEMD on different fault distances

由表1可知，基于EEMD算法的测距结果误差率普遍比EMD算法的误差率低，这进一步说明了通过EEMD算法能很好地解决EMD算法无法解决的频谱混叠问题，从而提高测距精度。

（2）设故障距离为110 km，发生三相短路，则不同过渡电阻下2种算法的测量结果如表2所示。

由表2可知，基于EEMD的测距算法在不同的过渡电阻（小于500Ω）下精度较高，误差率最大不超过0.3%，与基于EMD的测距算法相比，精度普遍有所提高。而当过渡电阻高达500Ω后，测距精度明显下降，本文认为该现象可能由以下原因造成：①过渡电阻过大会导致反射的行波能量迅速下降，从而影响了固有频率的识别和提取；②过渡电阻大到一定程度后与线路的特征阻抗相比不宜忽略，若仍采用前文推导的测距公式测距自然会产生较大的误差。

表2 不同过渡电阻下EMD和EEMD的测量结果Tab.2 Results by using EMD and EEMD on different transition resistances

（3）设故障距离为110 km，过渡电阻为1Ω，则不同故障类型下两种算法的测量结果如表2所示。为了避免赘述，单相故障和两相故障分别以A相和BC相为例（AG表示A相接地故障；BC/BCG表示BC相短路故障/BC相短路接地故障；ABC/ABCG表示ABC三相短路故障/ABC三相短路接地故障）。

表3 不同故障类型电阻下EMD和EEMD的测量结果Tab.3 Results by using EMD and EEMD on different fault types

从表3可以看出，不管故障类型是单线接地还是相间短路或相间短路接地，采用EEMD算法的测距结果误差都不超过0.3%，相比EMD算法的结果，精度提高约0.2%至0.5%。从表中的数据还可以看出，单相接地的测距结果的误差率普遍比其他两种故障类型大一些，这是由于当线路发生单相接地故障时，行波会穿越故障点并在测量点和线路连接点间来回传播，从而导致固有频率主成分的提取有相对大一点的误差。

3.5 其他类型线路

前几节以A型（2段）线路为算例，通过大量仿真验证了所提方案的准确性，本节以B型（3段）线路为例简单说明其他类型线路的仿真验证过程。

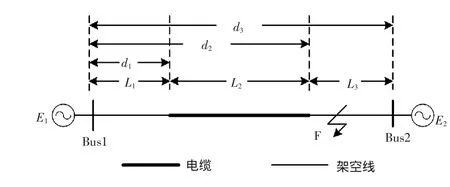
图11 B型线路故障示意Fig.11 Fault schematic of Type B transmission line

如图11所示，假设测量端位于Bus1端，从测量端向右各线路长度依次为L1，L2和L3，各线段最右端至测量端长度分别为d1，d2和d3，故障发生在第2段架空线即L3段。

对采集得到的暂态电流进行相模变换后，选取适当的模量进行EEMD分解和频谱分析得到故障信号的固有频率主成分fdf，利用该频率下的架空线和电缆的行波波速分别计算d1、d2和d3的主频fd1、fd2和fd3，将fdf和各区段主频进行大小比较，得到，此时k=3，说明故障区段位于L3段。根据式（2）计算Lf，最后利用式（3）即可得到最终的故障距离。

从以上A、B型线路系统的故障测距过程可知，对于B、C、D型线路系统和混合线路为多段系统，在仿真建模过程中需要注意根据混合线路的排列顺序依次建立模块，采集故障信息和提取固有频率环节和A型混合线路的处理过程一致，由于线路区段较多，因此在距离计算时，需要注意避免混淆各区段的主频以准确判断故障区段。

4 结语

针对混合线路行波的严重频谱混叠问题，提出了采用EEMD求解IMF的方法，引入了MUSIC算法准确地提取了固有频率主成分，推导了混合线路故障测距的公式。通过EMD和EEMD两种算法的仿真对比表明，EEMD能更好地克服模态混叠现象，测距精度更高。

[1]李博雅，杨耀，杨立红（LiBoya，Yang Yao，Yang Lihong）．高压直流输电线路单端故障测距组合算法（A combined method of single-ended fault location for HVDC transmission lines）[J]．电力系统保护与控制（Power System Protection and Control），2014，42（3）：116-121．

[2]廖凯，何正友，李小鹏（Liao Kai，He Zhengyou，Li Xiaopeng）．基于行波固有频率的高压直流输电线路故障定位（Fault location ofHVDC transmission line based on the natural frequency of traveling wave）[J]．电力系统自动化（Automation of Electric Power Systems），2013，37（3）：104-109．

[3]徐高，龚庆武，关钦月，等（Xu Gao，Gong Qingwu，Guan Qinyue，et al）．利用行波固有频率和原子能量熵的故障选相方法（A fault-phase selection method based on natural frequency of traveling wave and atomic energy entropy）[J]．电网技术（Power System Technology），2014，38（6）：1688-1693．

[4]尚秋峰，康丹，李青，等（Shang Qiufeng，Kang Dan，Li Qing，et al）．基于单节点重构改进小波包的电力系统谐波分析算法（Power system harmonic analysis algorithm based on wavelet packet improved by single-node reconstruction）[J]．电力系统保护与控制（Power System Protection and Control），2011，39（3）：74-77，94．

[5]牛雪梅，黄晋英，潘宏侠，等（Niu Xiemei，Huang Jinying，Pan Hongxia，et al）．免疫优化盲源分离算法在故障诊断中的应用（Immune optimization algorithm for blind source separation and its application on fault diagnosis）[J]．振动、测试与诊断（Journal of Vibration，Measurement&Diagnosis），2012，39（2）：304-311，347．

[6]陈自宽，翟宏琛，母国光（Chen Zikuan，ZhaiHongchen，Mu Guoguang）．用多重交织抽样方法消除频谱混叠（Eliminating aliasing by multiple interlacing samplings）[J]．信号处理（Signal Processing），1999，15（1）：1-5．

[7]夏璐璐，何正友，李小鹏，等（Xia Lulu，He Zhengyou，Li Xiaopeng，et al）．基于行波固有频率和经验模态分解的混合线路故障测距方法（A fault location method based on natural frequencies and empirical mode decomposition for mixed overhead-cable lines）[J]．电力系统自动化（Automation of Electric Power Systems），2010，34（18）：67-73．

[8]孙一航，武建文，廉世军，等（Sun Yihang，Wu Jianwen，Lian Shijun，et al）．结合经验模态分解能量总量法的断路器振动信号特征向量提取（Extraction of vibration signal feature vector of circuit breaker based on empirical mode decomposition amount of energy）[J]．电工技术学报（Transactions of China Electrotechnical Society），2014，29（3）：228-236．

[9]查丛梅，王长江，魏云冰，等（Zha Congmei，Wang Changjiang，WeiYunbing，et al）．一种基于EMD的谐振接地系统选线新方法（A new method of the resonant grounding system fault line detection based on EMD）[J]．电力系统保护与控制（Power System Protection and Control），2014，42（14）：100-104．

[10]袁娜，朱永利，梁涵卿（Yuan Na，Zhu Yongli，Liang Hanqing）.结合矩形窗的EEMD局部放电信号去噪（EEMD de-noising method using rectangular window）[J].电力系统及其自动化学报（Proceedings of the CSU-EPSA），2015，27（3）：54-58.

[11]王晓卫，魏向向，高杰，等（Wang Xiaowei，Wei Xiangxiang，Gao Jie，et al）.基于EEMD与SVM的配电网故障选线方法（A novel fault line selection method based on EEMD-Hilbert and SVM for distribution network）[J].电力系统及其自动化学报（Proceedings of the CSU-EPSA），2014，26（12）：55-61.

[12]Wu Z，Huang N E．A study of the characteristics ofwhite noise using the empirical mode decomposition method[J]．Proceedings of the Royal Society of London，Series A，2004，460（2046）：1597-1611．

[13]ZhaohuaWu，Huang N E．Ensemble empirical mode decomposition：a noise-assisted data analysis method[J]．Advances in Adaptive Data Analysis，Theory and Applications，2009，1（1）：1-41.

[14]杨关春，陈平，高鹏（Yang Guanchun，Chen Ping，Gao Peng）．基于PSCAD单芯电力电缆故障暂态仿真建模（Transient simulation modeling of single power cable fault based on PSCAD）[J]．山东理工大学学报：自然科学版（Journal of Shandong University of Technology：Natural Science Edition），2013，27（2）：50-53．

[15]董新洲，葛耀中，贺家李，等（Dong Xinzhou，Ge Yaozhong，He Jiali，et al）．输电线路行波保护的现状与展望（Statusquo and prospect of travelling waves protection of transmission lines）[J]．电力系统自动化（Automation of Electric Power Systems），2000，24（10）：56-61．

[16]王珺，董新洲，施慎行（Wang Jun，Dong Xinzhou，Shi Shenxing）．考虑参数依频变化特性的辐射状架空配电线路行波传播研究（Traveling wave transmission research for overhead lines of radial distribution power systems considering frequency characteristics）[J]．中国电机工程学报（Proceedings of the CSEE），2013，33（22）：96-102．

[17]许伯强，孙丽玲，李和明（Xu Boqiang，Sun Liling，Li Heming）．基于多重信号分类与模式搜索算法的笼型异步电动机转子断条故障检测新方法（A detection method for broken rotor bar fault in induction motors based on multiple signal classification and pattern search algorithm）[J]．中国电机工程学报（Proceedings of the CSEE），2012，32（9）：93-99．