基于Deb可行性规则的粒子群算法的液压缸优化设计
2015-04-16泸州职业技术学院机械工程系四川泸州646005
(泸州职业技术学院 机械工程系, 四川 泸州 646005)
引言
液压缸是液压系统中常用的一种执行元件,是把液体的压力能转变为机械能的装置,主要用于实现机构的直线往复运动,也可以实现摆动,其结构简单,工作可靠。用它来实现往复运动时,可免去减速装置,并且没有传动间隙,运动平稳,因此在各种机械的液压系统中得到广泛应用。
文献[1]针对长行程液压缸的冲击现象,建立数学模型,采用约束随机方向搜索法对长行程液压缸的结构参数进行优化设计,对缓冲装置中的结构参数(圆锥形凸台长度和锥角)进行优化设计,得出了圆锥形凸台长度和锥角的最优设计参数, 减少了液压系统的冲击,改善了液压缸的缓冲性能。文献[2]提出将弹性理论、优化理论和有限元法结合运用于液压缸的优化设计,改善了液压缸的应力状况,并可精确地确定液压缸的结构尺寸,减轻液压缸的重量。文献[3]对一种高推力结构的液压缸,采用SUMT内点罚函数寻优方法,对其结构参数进行优化设计。文献[4]阐述了内、外柱支撑力相等的双伸缩液压缸的组成、结构、工作原理、主要技术参数、设计思路、用途及特点。内、外柱支撑力相等的双伸缩液压缸的出现,打破了传统双伸缩液压缸的结构、原理和特性,使液压缸增添了新的品种。文献[5]针对液压缸活塞杆与缸体由于受轴力和横向力的共同作用而产生弯曲变形导致液压缸整体失稳的问题,分别对活塞杆和缸体建立挠曲性微分方程,确定活塞杆与缸体间隙处最大挠度,再建立关于挠度的非线性方程组,获得计算液压缸临界载荷的超越方程。结合参数化有限元优化设计技术,获取体积约束条件下液压缸的合理尺寸,通过与Ritz法计算结果比对和实验验证可知,该算法能够较好地优化液压缸结构参数,满足工程实际应用需要。
借鉴上述研究成果,文中应用基于Deb可行性规则的粒子群算法,对带有反柱结构液压缸的结构参数进行优化设计。最后,给出工程设计实例,优化结果表明新方法的有效性和稳健性。
1 带有反向柱结构液压缸的数学模型
1.1 带有反向柱液压缸的机械结构
本研究所讨论的液压缸带有反向柱结构,其机械结构如1所示。这种液压缸适用于液压支架,特别是用于非开挖顶管机、市政工程盾构机、压力机等领域意义更加显著。

图1 带有反向柱液压缸的机械结构
图1中,D1与D2分别为缸体的外径与内径;D3与D4分别为活塞柱的外径与内径;D5与D6分别为反向柱的外径与内径;p为液体的工作压力;P为液压缸的推力。
液压缸的优化设计问题包括:液压缸重量最轻、液压缸外径最小、液压缸推力最大等。本研究主要讨论液压缸重量最轻优化问题。在推力P和工作压力p给定条件下,使液压缸径向有效截面积最小,进而使缸体使用材料量最小。
1.2 决策变量与目标函数
上述优化问题可以转化为机械设计优化问题。即在满足推力的要求下,使液压缸用材量最少,即液压缸径向断面面积S最小。
设寻优变量为x=[x1,x2,…,x6]T=[D1,D2,…,D6]T,则设计液压缸重量最轻问题可转化为如下目标函数:
1.3 约束条件
带有反向柱结构液压缸优化设计的约束条件包括:结构尺寸条件、压力条件、强度条件及稳定性条件。
1) 液压缸结构条件
设计变量的边界条件确定,是根据结构的要求(如密封件的尺寸等)加以考虑。取各设计变量的尺寸要求为:
则液压缸的结构尺寸约束条件为:
g1(x)=-x1+x2+20≤0
(2)
g2(x)=-x2+x3+16≤0
(3)
g3(x)=-x3+x4+16≤0
(4)
g4(x)=-x4+x5+10≤0
(5)
g5(x)=-x5+x6+10≤0
(6)
2) 压力条件
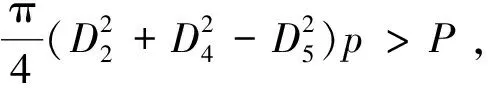
(7)
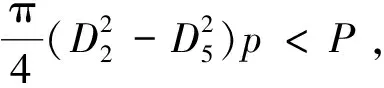
(8)
3) 液压缸缸体强度条件
(9)
式中:ns1为安全系数;σs为材料屈服极限。
4) 液压缸活塞柱强度条件及稳定性条件
(10)
式中:ns2为安全系数;σs为材料屈服极限。




于是,得约束条件:
(11)
5) 液压缸反向柱强度条件
(12)
式中:ns3为安全系数;σs为材料屈服极限。
综上所述,带有反向柱结构的液压缸重量最轻优化设计是包含11个不等式约束的6维非线性规划问题。
2 基于Deb可行性规则的粒子群算法
2.1 粒子群算法描述
PSO算法首先在可行解空间和速度空间随机初始化粒子群,即确定粒子的初始位置和初始速度,其中位置用于表征问题解。例如,D维搜索空间中的第k个粒子的位置和速度可分别表示为xk=(xk,1,xk,2,…,xk,D)T和vk=(vk,1,vk,2,…,vk,D)T,k=1,2,…,N(N为种群规模)。通过评价各个粒子的适应度,确定t(t=1, 2,…,T,T为最大进化代数)时刻粒子所经过的最优位置Pk=(Pk,1,Pk,2,…,Pk,D)T及群体所发现的全局最优位置G=(G1,G2,…,GD)T,再按下面的公式(13)与公式(14)分别更新粒子的速度和位置。
(13)

d=1, 2,…,D;t=0, 1, …,T-1
(14)

为了克服线性递减权重的不足,本研究取[6,7]:
(15)
其中,wsta、wend为初始、终止惯性权重。
2.2 约束处理方法
液压缸约束优化设计问题的求解难点在于如何处理约束条件。本研究采用Deb基于可行性规则[9-14]处理该约束条件,首先引入比较两个候选解(即粒子位置)的可行性规则。
规则1:若两个候选解都是可行解,则目标函数值小的获胜。
规则2:若两个候选解都是不可行解,则约束违反度小的获胜。
规则3:若一个是可行解而另一个是不可行解,则可行解获胜。
在规则2中,需要应用候选解的约束违反度比较两个不可行解。
本研究将候选解x的约束违反度定义为[13]:
(16)
式中:
显然,当x为可行解时,有fv(x)=0。
2.3 算法实现
基于Deb可行性规则的粒子群算法采用MATLAB软件编程实现,具体算法设计如下:
步骤1:设定种群规模、初始惯性权重、终止惯性权重、加速度常数、最大飞行速度、最大迭代代数,随机初始化粒子群的位置与速度,并计算各粒子适应度。
步骤2:将第i个粒子的当前位置设置为个体极值(pBest),设置群体中全局最佳粒子位置为全局极值(gBest)。
步骤3:根据式(13)和式(14)对粒子群中全局最优粒子的速度和位置进行更新。
步骤4:计算每个粒子的适应度f(xi),i=1,2,…,N。
步骤5:如果粒子i的适应度优于自身pBest的适应度,pBest更新为该粒子的当前位置xi。
步骤6:如果粒子i的适应度优于gBest的适应度,gBest更新为该粒子的当前位置xi。
步骤7:判断算法是否满足终止条件,若是则输出相应优化变量,程序运行结束;否则转步骤3。
3 工程设计实例与讨论
按重量最轻原则,设计带有反向柱结构的液压缸。已知条件:推力P=1800 kN,压力p=31.5 MPa,液压缸最大工作长度L=2500 mm;材料为27SiMn,其屈服极限σs=850 MPa;液压缸缸体、活塞柱、反向柱的外径与内径尺寸为:[D1,D2,…,D6]T=[300 230 210 180 90 60]T。安全系数ns1=3,ns2=ns3=2;活塞杆稳定安全系数nst=4。
PSO算法控制参数:种群规模N=60,初始惯性权重wsta=1.2,终止惯性权重wend=0.2,加速度常数Φ1=Φ2=2,最大飞行速度vmax,d=0.3(xmax,d-xmin,d) (d=1, 2,…, 6),最大迭代代数T=500。
优化结果x*=[275.02, 244.14, 224.02, 198.48, 137.20, 120.86]Tmm,目标函数f(x*)=24379.51 mm2。带有反向柱结构液压缸的优化设计进化曲线如图2所示。

图2 液压缸的优化设计进化曲线
对优化结果取整,得x*=[275, 244, 224, 198, 137, 121]Tmm,则相应的目标函数为f(x*)=24495.78 mm2。根据优化前液压缸的尺寸可知,液压缸径向断面面积S=41861.72 mm2。液压缸优化设计前与优化设计后的结果比较分析见表1。
通过上述分析可得出,文中采用基于Deb可行性规则的粒子群算法,其求解精度为24495.78 mm2,使液压缸径向断面面积减少41.48%,优化效果明显。利用优化结果对约束条件进行检验,约束函数值g=[-1.100×101,-4.000×100,-1.000×101,-5.100×101,-6.000,-1.789×105,-7.914×105,-1.633,-8.593×101,-3.119×104,-3.637×101]T,即满足全部约束条件。文中的求解结果中,靠近约束边界的变量取值更多,符合机械约束优化等大多数工程约束优化问题取得最优解通常位于约束边界的客观实际。工程设计实例表明文中算法的稳健性好,约束处理方法得当,算法效率高。

表1 液压缸优化设计前、后结果的比较分析
4 结论
应用粒子群算法,对带有反向柱的液压缸结构参数进行优化设计,能使液压缸在保持合理应力水平情况下,液压缸的重量减轻约41%,效果显著。对液压缸优化设计具有一定参考价值。
(1) 讨论了液压缸结构设计约束优化问题的约束处理方法,建立了一种基于Deb可行性规则的动态自适应罚函数的约束处理方法,使惩罚函数更为简单,提高优化计算效率;
(2) 应用基于Deb可行性规则的动态自适应罚函数法将机械约束优化设计问题转化为无约束优化模型,算法中初始群体在设计参数的上下边界范围内产生,并应用粒子群算法求解该问题;
(3) 给出了典型的工程优化实例,并与优化前的结果进行对比检验,文中结果符合约束条件和设计要求,且比优化前具有更优的目标函数值,表明算法和约束处理方法是有效且可靠的;
(4) 所提出的基于Deb可行性规则改进惩罚策略,使粒子群算法更能有效处理带非线性约束的数值优化问题,算法的工程实用性增强,可以推广到其他工程约束优化问题。
参考文献:
[1]张剑慈.液压缸的优化设计[J].机械制造,2012,50(9):59-61.
[2]曹苹.长行程液压缸优化设计[J].苏州丝绸工学院学报,2000,20(3):53-57.
[3]刘春生,唐凯.高推力液压缸的优化设计[J].矿山机械,1994,22(4):39-42.
[4]隋文臣.内外柱支撑力相等的双伸缩液压缸的研究[J].煤炭技术,2004,23(9):15-16.
[5]林荣川,郭隐彪,魏莎莎,等.液压缸临界载荷计算和最优设计[J].中国机械工程,2011,22(4):389-393.
[6]何兵,车林仙,罗佑新.求十面体变几何桁架机器人位置正解的改进粒子群算法[J].机械设计,2008,25(11):31-34.
[7]李洁,车林仙,何兵.按传动角优化曲柄滑块机构的约束粒子群算法[J].机械设计,2012,29(1):65-68.
[8]何兵,车林仙,刘初升.结合机械设计约束处理的差分进化算法[J].机械设计,2012,29(4):17-21.
[9]司呈勇,兰天,胡俊杰,等.关于惩罚函数中惩罚系数的讨论[J].控制与决策,2014,29(9):1707-1710.
[10]梁昔明,龙文,秦浩宇,等.基于种群个体可行性的约束优化进化算法[J].控制与决策,2010,25(8):1129-1132.
[11]Deb K.An Efficient Constraint Handling Method for Genetic Algorithms[J].Computer Methods in Applied Mechanics and Engineering,2000,186(234):311-338.
[12]车林仙,程志红.工程约束优化的自适应罚函数混合离散差分进化算法[J].机械工程学报,2011,47(3):141-151.
[13]车林仙,何兵,程志红.扇形采样约束多目标差分进化算法及工程应用[J].机械工程学报,2013,49(23):150-160.
[14]董芬英.基于可行性规则的混合粒子群的盲源分离[J].科技信息,2013,30(3):98-99.
