矩形密封圈应力和接触压力的影响因素
2015-04-16,,,
, , ,
(1.武汉科技大学 机械自动化学院, 湖北 武汉 430081;2.武汉科技大学 冶金装备及其控制教育部重点实验室, 湖北 武汉 430081)
引言
叶片式液压摆动油缸的旋转密封与叶片密封耦合处,通常采用O形截面橡胶密封圈[1],其耦合面容易产生空隙,难以达到预期的密封效果。矩形橡胶密封圈以其结构简单、互换性好等特点可用来替代O形密封圈,取得较好的密封效果。近来,国内外学者对橡胶密封圈的密封机理及性能做了许多研究。谭晶等分析比较了O形密封圈和矩形密封圈的密封性能及影响因素[2-4]。周志鸿研究了预压缩率和油压对O形圈变形与受力的影响,得到预压缩率和油压对Von-Mises(以下简称范·米塞斯)应力分布及接触压力影响规律[5], 杨春明分析了O形截面密封圈密封间隙、 油压对范·米塞斯应力和密封面最大接触压力的影响,以及它们之间的相互关系[6]。俞鲁五分析了一种静密封用密封件——矩形密封圈,阐述了矩形密封圈的工作机理和特点,并与O形密封圈进行了对比[7]。根据已有文献的研究,矩形密封圈在较高介质压力下的挤出现象及防止措施研究并没有受到关注。本研究以DK矩形密封圈为研究对象,建立密封结构的二维轴对称模型,利用大型有限元软件ABAQUS研究该矩形密封圈在不同预压缩量和不同介质压力下的范·米塞斯应力及其在密封面上的接触压力分布情况。
1 矩形密封圈接触压力模型
1.1 计算模型
研究选用DK系类矩形密封圈,尺寸:截面宽w=5.16 mm,内径d= 114 mm,缸体倒角r=0.3°。
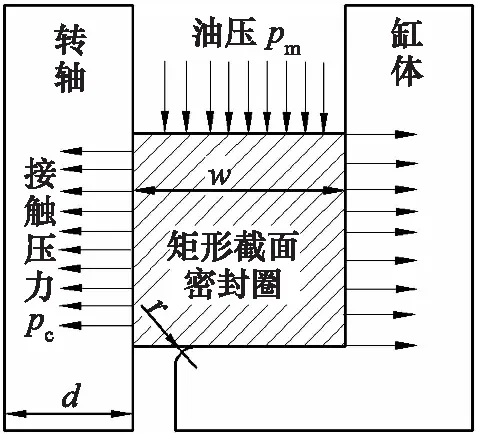
图1 计算模型
1.2 密封圈材料
密封圈材料为丁腈橡胶(NBR),硬度为IRHD85。
由于橡胶具有可高度变形,是超弹性体且近似不可压缩等特点,密封结构具有高度非线性,因此在本研究中做了如下假设:
① 矩形密封圈蠕变不引起体积变化;
② 矩形密封圈材料的拉伸与压缩蠕变性质相同;
③ 矩形密封圈受到的横向压缩视为由约束边界的指定位移引起的。
选用Mooney-Rivlin模型描述橡胶超弹性材料的力学特性,其函数表达为:
W=C1(I1-3) +C2(I2-3)
材料常数C1和C2分别取1.87和0.47[2]。
1.3 有限元模型
采用有限元软件Abaqus,利用自身的网格划分功能,建立有限元模型如图2所示,单元类型为平面轴对称CAX4RH单元。通过对模型中缸体施加x方向上的位移载荷来模拟矩形密封圈径向受压的预压缩过程,密封圈与缸体之间选用库伦摩擦模型,摩擦系数为0.1[8];在矩形密封圈与密封介质接触的表面施加均匀分布的压力载荷p,来模拟介质压力。
根据实际加工情况考虑,挡圈的厚度取1 mm,挡圈材料选用PTFE,弹性模量为500 MPa,泊松比为0.4,挡圈径向不受压缩,截面宽度为密封圈受压缩后的截面宽度。

图2 无挡圈有限元模型
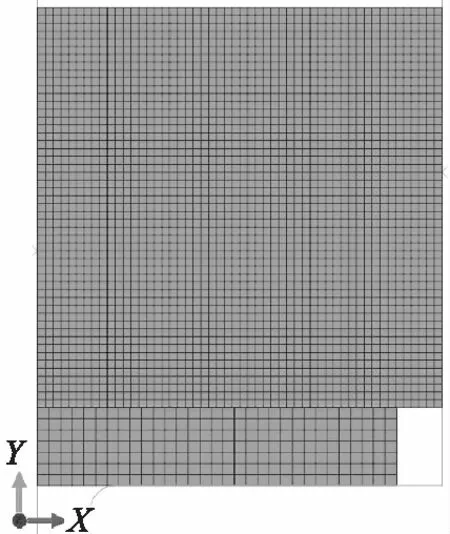
图3 带有挡圈的有限元模型
2 结果及数据分析
2.1 不同介质压力下无挡圈密封圈的应力
影响密封圈最大等效应力的因素主要有:密封圈的压缩率、介质压力、密封圈间隙处倒角、摩擦系数等。主要研究了压缩率与介质压力对最大范·米塞斯应力和密封面接触压力的影响。根据DK系列密封圈的标准要求,压缩量在0.28~0.58 mm之间,取压缩量为0.58 mm,通过对密封圈与介质接触的表面施加不同的载荷,分别得到矩形密封圈在5 MPa、10 MPa、15 MPa、20 MPa介质压力下的应力分布云图,如图4所示。
范·米塞斯应力反映了截面上各主应力差值的大小,一般来说,范·米塞斯应力越大,越会加速橡胶材料的松弛,造成刚度下降,容易出现裂纹[8]。
由于密封间隙的存在,密封圈被挤入密封间隙,由图4可以看出随着介质压力的增加,密封圈的挤出变形量也在增加。矩形密封圈的最大范·米塞斯应力,主要集中在间隙处橡胶变形较大位置。其他部位的范·米塞斯应力分布较均匀,没有应力集中现象,符合材料的应力应变规律。且根据图5可知,在其他条件不变的情况下,最大范·米塞斯应力p随着压缩量x的增加而增加,且几乎成线性增长。

图4 无挡圈时密封圈在不同介质压力条件下的应力分布云图

图5 预压缩量与最大范·米塞斯应力曲线
2.2 密封间隙对密封圈应力的影响分析
由于转子和定子为间隙配合,在加工精度一定的条件下,密封间隙会直接影响到密封圈的挤出量,进而影响到密封圈上范·米塞斯应力值的大小及分布情况。通过设置不同的密封间隙,在保证其他条件不变的情况下,得到密封间隙x1与矩形密封圈上最大范·米塞斯应力值的关系,如图6所示。

图6 密封间隙与密封圈上最大范·米塞斯应力关系曲线
可见随着密封间隙的增大,密封圈上的最大等效应力也随之增大。这是由于随着密封间隙的增大,密封圈的挤出量也增加,橡胶密封圈的变形量就越大,根据橡胶的应力应变曲线可知,橡胶变形量超过一定值的时候,最大等效应力就会呈指数增加,图6的曲线与此规律吻合。因此,为了防止密封挤出,降低密封圈上的范·米塞斯应力,应尽量减小密封间隙。在其他条件相同时,不同介质压力下的密封圈最大范·米塞斯应力变化曲线如图7所示,随着介质压力的提高,最大等效应力也不断增加,且几乎呈线性增加。密封圈上密封面的接触压力大小反应了密封圈的密封能力,以转子与密封圈接触面为研究对象,得到不同的介质压力条件下该密封面上的接触压力pc曲线,图8所示。
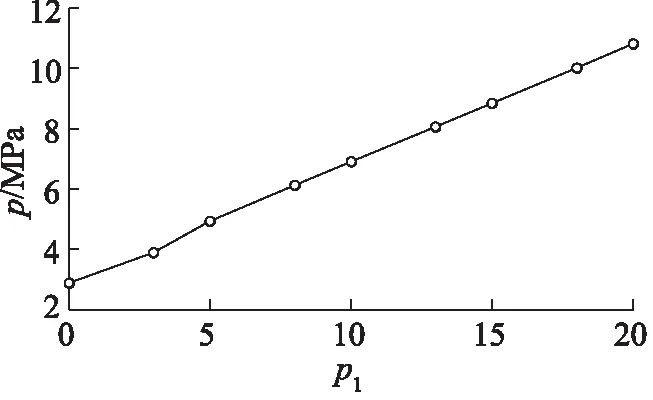
图7 不同介质压力条件下的最大范·米塞斯应力
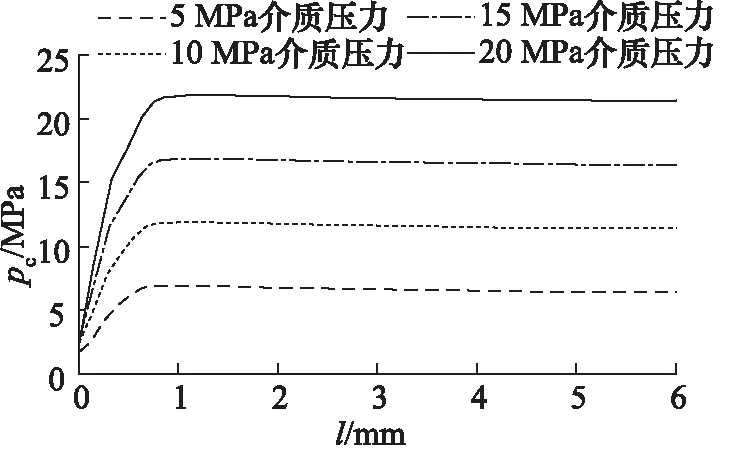
图8 不同介质压力下沿Y轴方向接触面上接触压力
密封面上的接触压力pc是由预压缩时的橡胶反弹力p0和介质压力pm共同作用产生,即[4]:
pc=p0+kpm
图8与图9的结果分析曲线与之吻合。随着介质压力的增加,密封面上的接触压力也是不断增加,接触面上沿Y轴方向,密封圈的接触压力在初始位置较低,只有少量单元接触压力小于介质压力,随着Y轴接触面长度值的不断增加,密封面接触压力稳定在大于介质压力值的一个水平,在靠近介质的地方,接触压力最高,可见密封面上的接触压力能够满足密封要求。但是预压缩量过大,橡胶的焦耳效应就越明显,也会严重影响密封圈的使用寿命,要选择合适的密封圈预压缩量。橡胶密封圈中,应力值较大的区域,密封材料越容易产生裂纹,随之产生密封圈的破坏,最终导致密封失效,密封圈中的集中应力严重影响了密封圈的使用寿命,因此在动密封中,矩形密封圈的预压缩量应当取较小值。
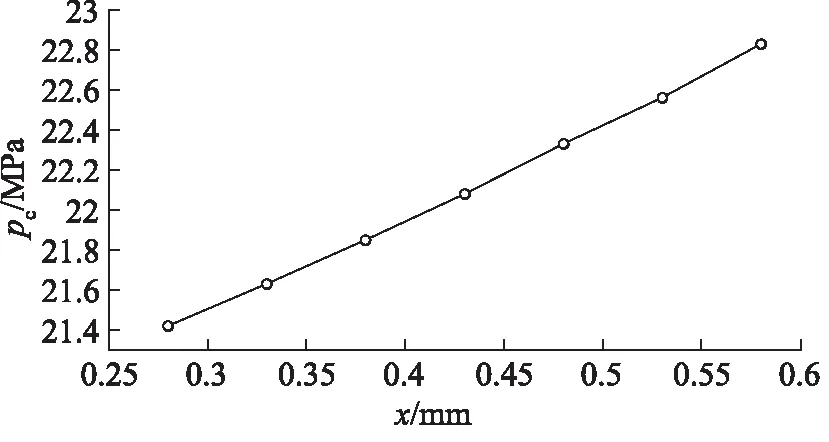
图9 密封面上最大接触压力和预压缩量的关系曲线
2.3 挡圈对密封圈应力分布的影响
采用在密封圈下方增添挡圈的方式来优化密封圈上的应力集中情况。根据所建立的有限元模型并求解,得到在不同介质压力下配有挡圈的密封圈应力分布云图,如图10所示。

图10 密封圈配有挡圈时,不同介质压力下的应力分布云图
可见矩形密封圈配合挡圈使用时,密封圈上的应力为均匀分布,无应力集中,应力集中于挡圈与缸体底部倒角位置,但由于挡圈的硬度较大,并没有挤出现象,密封圈上的应力分布得到了明显优化,挤出现象得到有效防止。
图11为在20 MPa介质压力时,沿Y轴方向上,与转子接触的密封面上接触压力的分布曲线,可见密封面上的接触压力分布和大小与未加挡圈时几乎是一样的,这说明橡胶密封圈的接触面上的密封能力没有发生变化。挡圈与转子的接触面压力小于介质压力,说明挡圈只起到支承密封圈,有效防止密封圈的挤出效应,并不起密封作用。
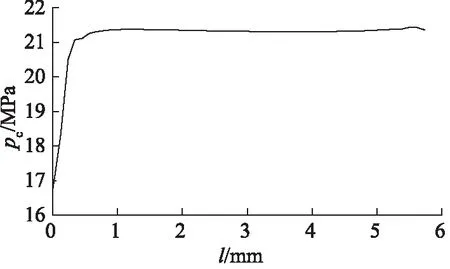
图11 20 MPa介质压力时密封面上的接触压力变化
3 结论
1) 矩形橡胶密封圈的应力集中在靠近缸体底部倒角的位置,最大范·米塞斯应力随着介质压力和预压缩量的增加而增加,且与密封间隙呈近似指数关系,分析结果符合橡胶的应力应变曲线规律,应尽量减小密封间隙。
2) 矩形橡胶密封圈的密封面接触压力分布较均匀,最大接触压力随着介质压力和预压缩量的增加而增加,且近似呈线性关系,用做旋转密封时,选用较小的预压缩量。
3) 矩形密封圈配合挡圈使用,挡圈并不起密封作用,但可以在不改变密封能力的前提下,防止密封挤出,明显改善矩形密封圈的应力集中现象,从而延长密封圈的使用寿命。
参考文献:
[1]蒋国璋,陈少华,谢良喜,等.O形旋转密封圈的密封性能有限元分析[J].机械设计与制造,2014,(6):178-181.
[2]谭晶,杨卫民,等.O形橡胶密封圈密封性能的有限元分析[J].润滑与密封密,2006,(9):65-69.
[3]陈国定,Haiser H,Hass W,等.O形密封圈的有限元力学分析[J].机械科学与技术,2000,19(5):740-742.
[4]谭晶,杨卫民,丁玉梅,等.矩形橡胶密封圈的有限元分析[J].润滑与密封,2007,32(2):36-39.
[5]周志鸿,张康雷.O形橡胶密封圈应力与接触压力的有限元分析[J].润滑与密封,2006,(4):86-89.
[6]杨春明,谢禹钧,韩春雨.基于Ansys的橡胶O形密封圈密封性能的有限元分析[J].石油与化工设备,2010,13(4):21-24.
[7]俞鲁五.介绍一种静密封用密封件——矩形密封圈[J].流体传动与控制,2006,(3):44-46.
[8]刘健,仇性启,薄万顺,等.橡胶O形密封圈最大接触压力数值分析[J].润滑与密封,2010,(9):41-44.
