基于非线性强度准则的城市固废本构模型

吕玺琳，黄茂松，王 蓉

（1.同济大学 岩土及地下工程教育部重点实验室，上海200092；2.同济大学 土木工程学院，上海200092；3.上海岩土工程勘察设计研究院有限公司，上海200032）

城市固体废弃物（municipal solid waste，MSW以下称为城市固废）由于组分复杂，加之生化降解等多种因素影响，其物理力学特性常较复杂.考虑到固废力学特性对填埋场稳定性及变形分析的重要性，因而有必要针对其强度和本构特性进行深入研究.

固废强度常通过线性Mohr-Coulomb准则描述，在当变形较大固废仍未破坏时，可采用应变10%～15%对应的抗剪强度确定［1］.以往试验结果表明，固废粘聚力一般在0～67kPa范围，摩擦角则位于0°～43°范围.随着龄期增长，固废充分降解后，粘聚力迅速降低甚至到0［2］.然而，线性 Mohr-Coulomb准则只能描述与常规土体力学性质相近的固废强度，对于大多数固废，其强度表现为非线性.Bray等［3］通过试验结果的分析，指出固废摩擦角随平均应力增大而降低，这进一步得到了Bareither等［4］试验结果和 Bhandari和 Powrie［5］的证实.Stark等［6］通过总结试验结果和填埋体稳定性强度参数反分析，进一步证实了固废强度的非线性特性.有关土体非线性强度目前已开展过一些探讨，并已建立了相应准则（如Baker［7］），但针对城市固废非线性强度特性还缺乏深入探讨，且与线性Mohr-Coulomb准则间的转换还值得进一步研究.

当前固废本构特性的研究多参照土体开展，如Jones和Dixon［8］利用Mohr-Coulomb理想弹塑性模型描述固废本构特性，用于填埋场稳定性分析.吕玺琳等［9］采用Mohr-Coulomb硬化模型研究固废本构特性，并分析了其失稳特性.Machado等［10］将固废看作纤维加筋相和泥状物复合体，提出了复合本构模型，冯世进等［11］则基于该模型建立了基于邓肯-张模型的复合本构模型.这些本构模型能合理描述固废应力-应变关系，但缺少对体变特性的探讨.受其复杂组分的影响，固废体变特性与常规土体可能差异较大.高丽亚等［12］通过大三轴试验指出，固废体变随围压增大反而减小，与土体体变规律相反，该特性也 得 到 其 他 试 验 结 果 （如 Machado 等［10］，Zhan等［2］，冯世进等［11］）的证实.

针对当前有关固废强度和本构描述存在的不足，本文基于幂函数形式的非线性破坏（屈服）准则，并采用合理的塑性势函数，建立了一个合理适用的固体废弃物本构模型，并通过对一系列三轴试验结果模拟进行了对比验证.

1 城市固废非线性强度准则

1.1 强度准则

为合理描述固废的非线性强度特性，采用幂函数强度准则［13］

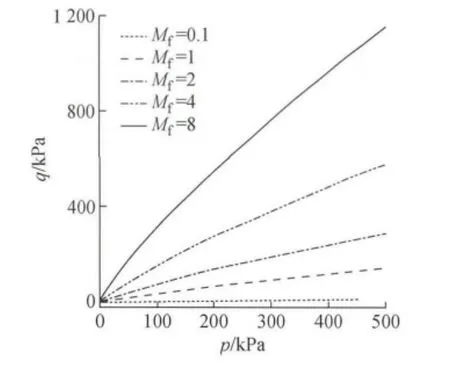
图1 Mf对强度的影响Fig.1 Influence of Mfon failure line

1.2 内摩擦角

对降解较充分的高龄期城市固废而言，其粘聚强度一般较小，为简单起见，忽略式（1）中的黏性项进行分析，峰值内摩擦角φ的计算公式为

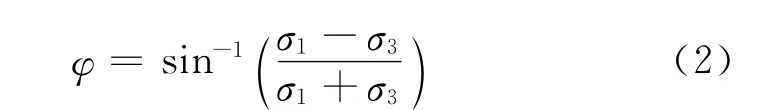
由于在三轴应力状态下，

图2 ξ对强度的影响Fig.2 Influence ofξon failure line

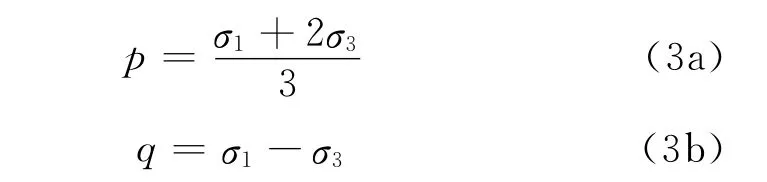
联立式（2）、（3），可得：

将式（4）代入式（1），可得：

从式（5）可看出，通过非线性强度准则得到的内摩擦角φ不仅与强度参数Mf和ξ有关，且与围压有关.φ的预测结果随各参数的变化规律如图3—5所示.φ随Mf增大而增大，σ3越小，φ增幅越大，随ξ增大而增大，Mf越大，增幅越大；随初始围压σ3增大而减小，Mf越大，降幅越大.

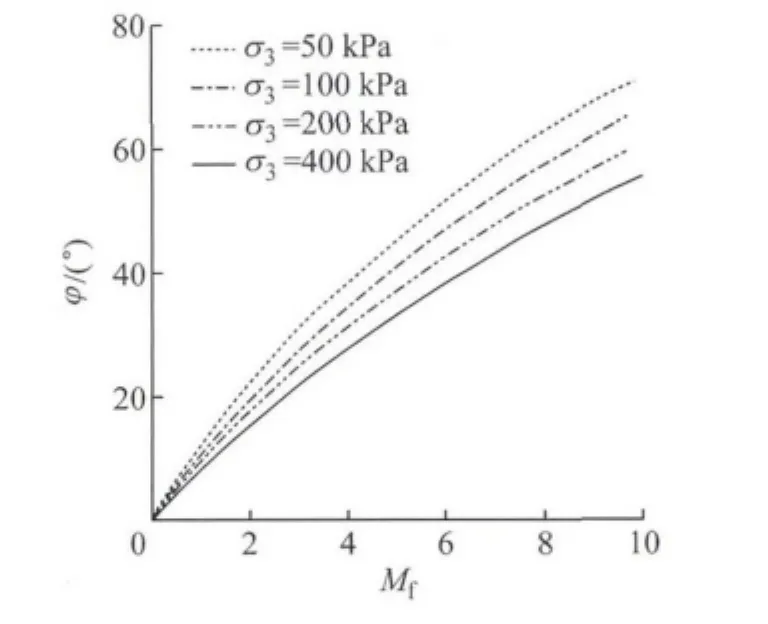
图3 Mf对内摩擦角的影响Fig.3 Influence of Mfon friction angle

2 城市固废本构模型

通过非线性强度准则建立屈服函数，并根据剪胀特性获得塑性势函数F和Q，分别为

图4 ξ对内摩擦角的影响（σ3＝100kPa）Fig.4 Influence ofξon friction angle

图5 初始围压对内摩擦角的影响Fig.5 Influence of confining stress on friction angle

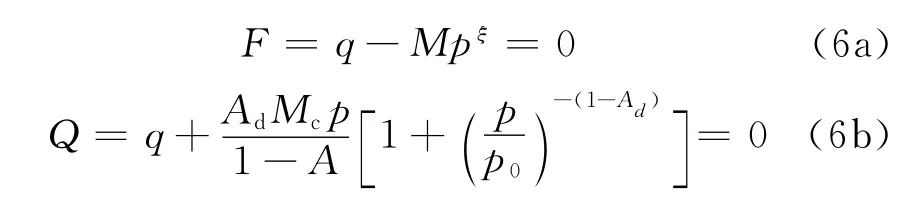
式中：平均应力p=σii／3；p0为初始平均应力；广义剪应力；偏应力sij=σij-δijp；M为反映屈服特性的参数；Mc代表剪缩向剪胀转换的临界应力比；Ad为剪胀性模型参数；A为拟合参数.

为合理描述固废的体变特性，剪胀参数比视为一个与初始围压有关的量，即表示为

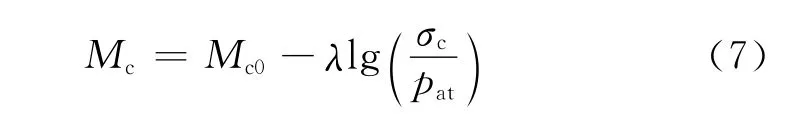
式中：Mc0、λ为描述剪胀特性的材料参数；σc为初始围压；pat=101.3kPa，为大气压力.

材料硬化特性采用增量形式的硬化准则［14］：

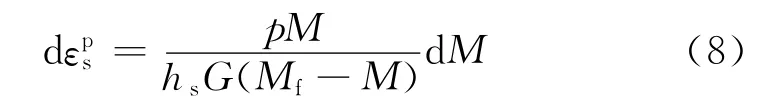
式中：G为弹性剪切模量；Mf为峰值状态应力比参

将式（8）进行积分，可得：

通过将以上建立的屈服函数、塑性势函数及硬化准则，得到弹塑性本构关系如下所示：

其中，弹塑性模量为：

利用式（6）、（8），得到硬化模量Hp为

为更好地模拟固废的应力-应变特性，体积模量K和剪切模量G均取为与材料孔隙比相关的函数：

式中：G0为剪切模量参数，ν为泊松比，e＊为孔隙比参考值；e为当前孔隙比.

3 三轴试验模拟验证

3.1 力学生物预处理（MBT）固废试验

首先模拟Bhandari和Powrie［5］针对力学生物预处理（mechanical-biological-treatment，MBT）固废三轴固结排水剪切试验结果.试样为直径10cm、高20cm的圆柱体，初始孔隙比为1.0.通过固废弹性特性选取参数G0、ν，根据试样孔隙特性选取e＊，Mf和ξ通过强度特性选取，Mc0和λ通过体变特性选取，hs为拟合参数.根据表1参数，对围压为50、100、200、400kPa条件下的试验结果进行模拟.

表1 模型参数Tab.1 Model parameter

采用幂函数非线性强度准则预测的固废抗剪强度结果如图6所示，预测值与试验值符合较好.

考虑剪胀参数随压力水平的变化，采用如图7所示的剪胀参数，模拟得到应力-应变关系曲线如图8所示，通过与试验对比表明，本模型能合理反映初始围压对应力-应变关系的影响特性.

图6 MBT固废强度预测Fig.6 Strength prediction of MBT MSW

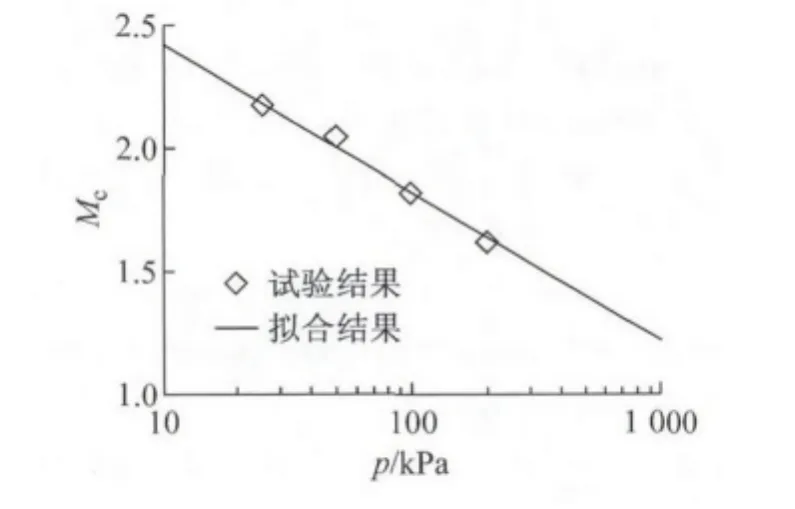
图7 Mc随平均应力的变化关系Fig.7 Variation of Mcwith mean pressure

3.2 成都某填埋场固废试验

进一步对李俊超等［15］的三轴固结排水剪切试验结果进行模拟.固废采自成都某填埋场5～15m深度处，直径为10cm、高度为20cm。根据现场实测结果，试样初始孔隙比取2.2.采用如表1所示的模型参数，对初始围压为50、100、150、250kPa条件下的4组试验结果进行模拟.通过本文非线性强度准则预测的强度值如图9所示，从图中可看出，该准则能合理反映平均应力对固废强度的影响.

应力-应变特性模拟结果与试验对比如图10a所示，模拟结果与试验基本一致.从试验结果可知，体缩型固废的体变与常规土体不同，即初始围压越大，体变反而越小.为合理描述这一特性，假定剪胀性参数与应力有关的量，这里取A=e-p／p0.从图10b的模拟结果可看出，采用该剪胀参数能合理反映试样随初始围压增大压缩性降低的现象，且模型预测结果与试验结果符合较好.

图8 MBT固废本构模拟Fig.8 Constitutive modeling of MBT MSW

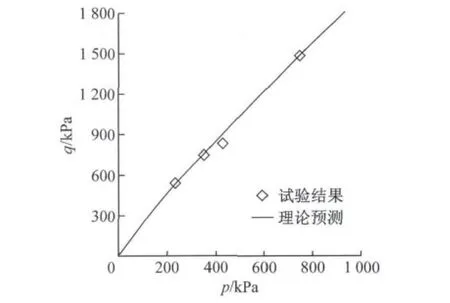
图9 成都填埋场固废剪切强度预测Fig.9 Shear strength prediction of MSW at Chengdu landfill

4 结论

为反映城市固废剪切强度随平均压力的变化，建立了一个幂函数非线性强度准则，并分析了剪切强度随参数的变化特性.进一步分析了向线性Mohr-Coulomb准则转换所得内摩擦角的变化规律，结果表明，该准则能合理反映摩擦角随围压而降低的规律，并与试验结果一致.基于增量双曲线硬化准则，并采用合理的塑性势函数，建立了一个适用于固废的非关联流动弹塑性本构模型.通过对一系列三轴固结排水试验结果的模拟表明，所建立的模型不仅能合理反映初始围压对应力-应变关系的影响，并能正确模拟体变随围压的变化.由于固废体变特性复杂，与常规土体可能差异较大，因而尚需开展进一步的试验和理论研究.

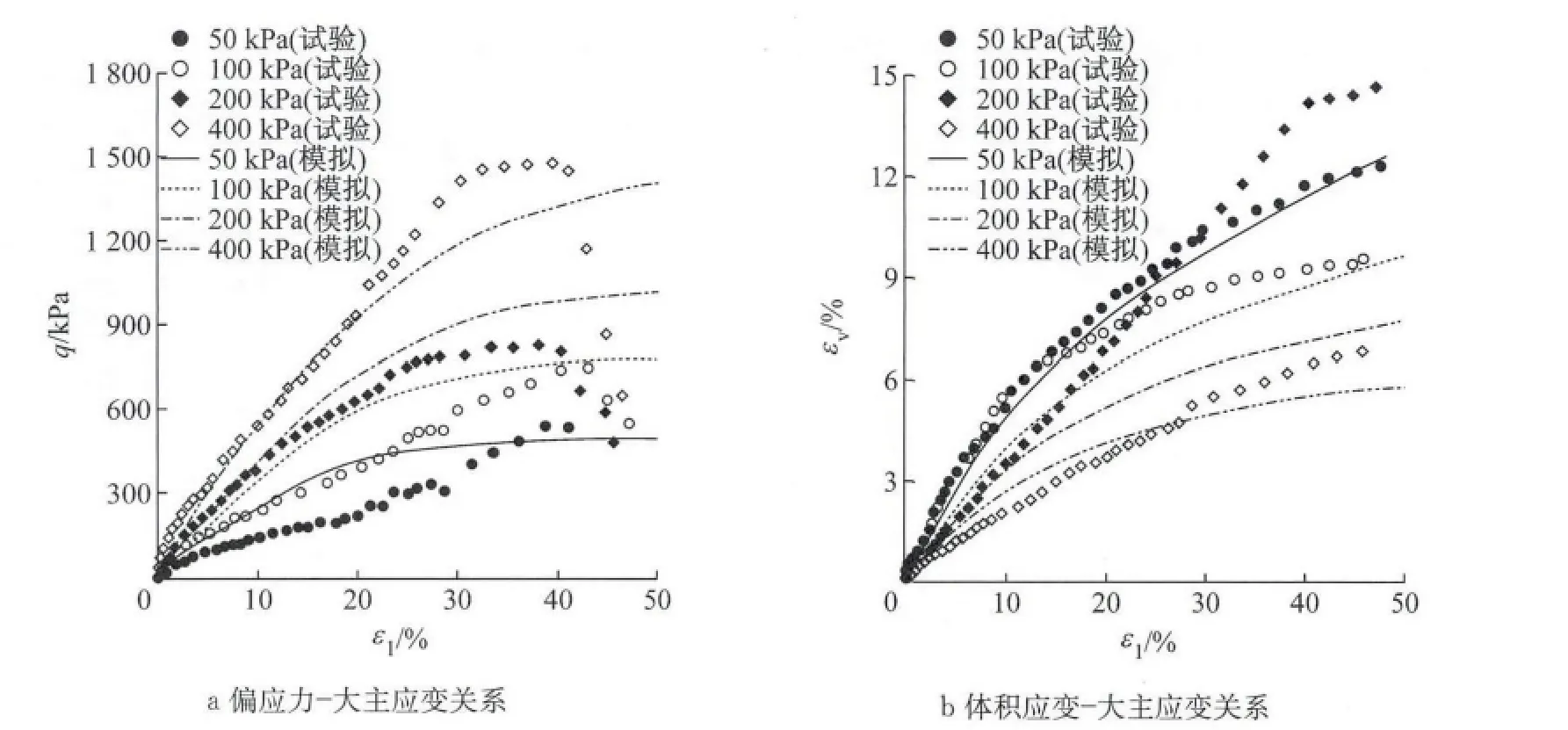
图10 成都填埋场固废本构模拟Fig.10 Constitutive modeling of MSW at Chengdu landfill

［1］ 冯世进，周子范，陈云敏，等.城市固体废弃物剪切强度参数的研究［J］.浙江大学学报：工学版，2005，39（7）：987.FENG Shijin，ZHOU Zifan，CHEN Yunmin，etal.Study on shear strength parameters of municipal solid waster［J］.Journal of Zhejiang University：Engineering Science，2005，39（7）：987.

［2］ Zhan T L T，Chen Y M，Ling W A.Shear strength characterization of municipal solid waste at the Suzhou landfill，China［J］.Engineering Geology，2008，97（3-4）：97.

［3］ Bray J D，Zekkos D，Kavazajian J E，etal.Shear strength of municipal solid waste ［J］.Journal of Geotechnical and Geoenvironmental Engineering，ASCE，2009，135（6）：709.

［4］ Bareither C A，Benson C H，Edil T B.Effects of waste composition and decomposition on the shear strength of municipal solid waste ［J］.Journal of Geotechnical and Geoenvironmental Engineering，ASCE，2012，138（10）：1161.

［5］ Bhandari A R，Powrie W.Behavior of an MBT waste in monotonic triaxial shear tests［J］.Waste Management，2013，33（4）：881.

［6］ Stark T D，Huvaj-Sarihan N，Li G.Shear strength of municipal solid waste for stability analyses［J］.Engineering Geology，2009，57（8）：1911.

［7］ Baker R.Nonlinear Mohr envelopes based on triaxial data［J］.Journal of Geotechnical and Geoenvironmental Engineering，ASCE，2004，130（5）：498.

［8］ Jones D R V，Dixon N.Landfill lining stability and integrity：the role of waste settlement［J］.Geotextiles and Geomembranes，2005，23（1）：27.

［9］ 吕玺琳，赖海波，黄茂松.饱和土体静态液化失稳理论预测［J］.岩土力学，2014，35（5）：1330.LÜ Xilin， LAI Haibo， HUANG Maosong.Theoretically predicting instability of static liquefaction of saturated soils［J］.Rock and Soil Mechanics，2014，35（5）：1330.

［10］ Machado S L，Miriam F C，Orencio M V.Constitutive model for municipal solid waste［J］.Journal of Geotechnical and Geoenvironmental Engineering，ASCE，2002，128（11）：940.

［11］ 冯世进，陈云敏，高丽亚，等.城市固体废弃物的剪切强度机理及本构关系［J］.岩土力学，2007，28（12）：2524.FENG Shijin，CHEN Yunmin，GAO Liya，etal.Shear strength mechanism and constitutive model of municipal solid waste［J］.Rock and Soil Mechanics.2007，28（12）：2524.

［12］ 高丽亚，冯世进，陈云敏，等.城市固体废弃物大直径三轴压缩试验研究［J］.同济大学学报：自然科学版，2007，35（12）：1602.GAO Liya，FENG Shijin，CHEN Yunmin，etal.Large-scale triaxial compression test for municipal solid waste［J］.Journal of Tongji University：Natural Science，2007，35（12）：1602.

［13］ Lu X，Lai H，Huang M，Nonlinear strength criterion for municipal solid waste［C］／／Computer Methods and Recent Advances in Geomechanics，London：Taylor &Francis Group，2014：279-284.

［14］ Pietruszczak S，Stolle F E.Deformation of strain softening material，part II：modelling of strain softening response［J］.Computers and Geotechnics，1987，4（2）：109.

［15］ 李俊超，朱斌，连宝琴，等.城市固体废弃物应变硬化机制与强度参数确定方法［J］.岩石力学与工程学报，2014，33（4）：826.LI Junchao，ZHU Bin，LIAN Baoqin，etal.Strain hardening mechanism and methods for determing strength parameters of municipal solid waste［J］.Chinese Journal of Ruck Mechanics and Engineering，2014，33（4）：826.